2023-2024学年人教版数学九年级下册 27.3位似同步测试卷(含答案)
文档属性
| 名称 | 2023-2024学年人教版数学九年级下册 27.3位似同步测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 379.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 10:50:13 | ||
图片预览


文档简介
第27章相似 27.3位似同步测试卷
一、选择题
1、如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为13,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点的坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
2、视力表的一部分如图,其中开口向上的两个“E”之间的变换是( )
A.平移 B.旋转 C.对称 D.位似
3、在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2).若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为( )
A.(5,1) B.(4,3) C.(3,4) D.(1,5)
4、如图,四边形ABCD和是以点O为位似中心的位似图形,若OA::3,则四边形ABCD与四边形的面积比为( )
A. 4:9 B. 2:5 C. 2:3 D. :
5、如图,在平面直角坐标系中,有两点A(4,2),B(3,0),以原点O为位似中心,A′B′与AB的相似比为,得到线段A′B′,正确的画法是( )
A B C D
6、如图,△ABC与△DEF是位似图形,相似比为2∶3,已知AB=4,则DE的长等于( )
A.5 B.6 C.9 D.
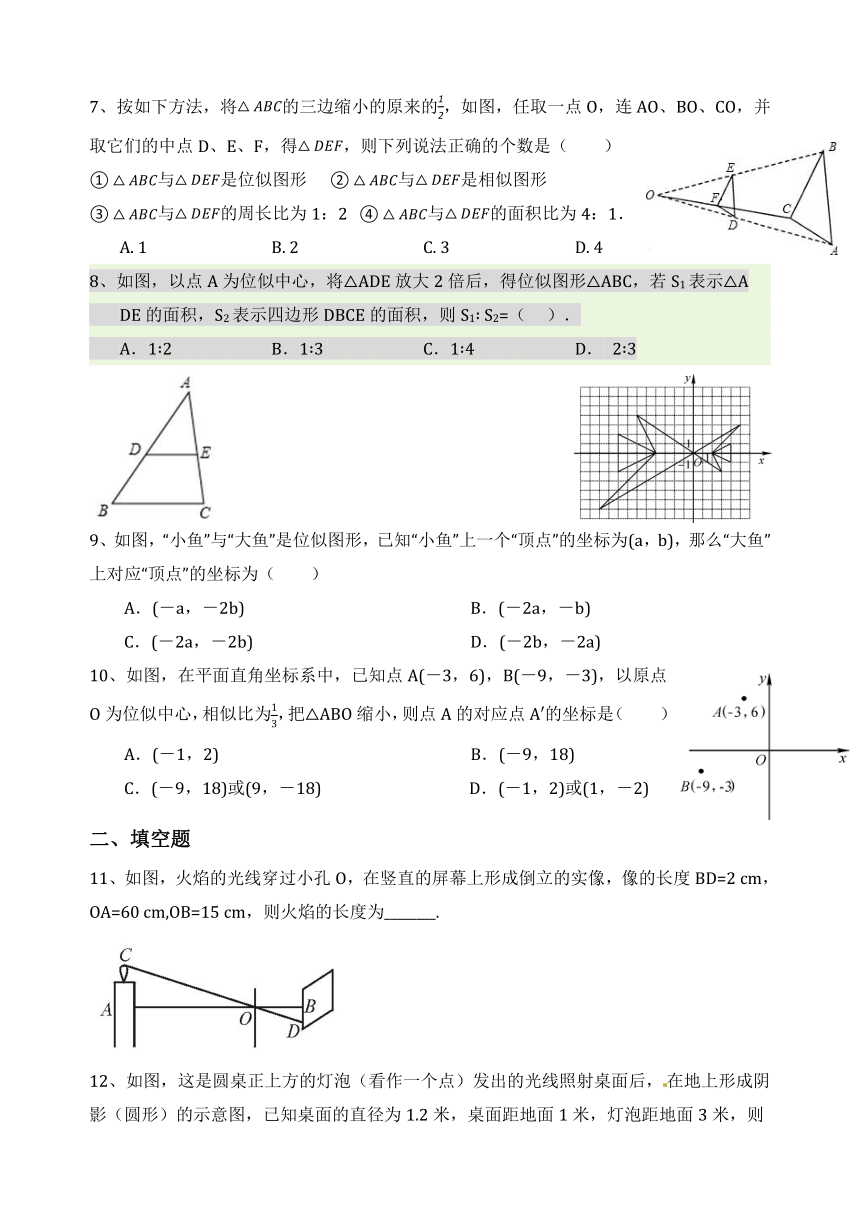
7、按如下方法,将的三边缩小的原来的,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得,则下列说法正确的个数是( )
与是位似图形 与是相似图形
与的周长比为1:2 与的面积比为4:1.
A. 1 B. 2 C. 3 D. 4
8、如图,以点A为位似中心,将△ADE放大2倍后,得位似图形△ABC,若S1表示△A DE的面积,S2表示四边形DBCE的面积,则S1∶ S2=( ).
A.1∶2 B.1∶3 C.1∶4 D. 2∶3
9、如图,“小鱼”与“大鱼”是位似图形,已知“小鱼”上一个“顶点”的坐标为(a,b),那么“大鱼”上对应“顶点”的坐标为( )
A.(-a,-2b) B.(-2a,-b)
C.(-2a,-2b) D.(-2b,-2a)
10、如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(-1,2) B.(-9,18)
C.(-9,18)或(9,-18) D.(-1,2)或(1,-2)
二、填空题
11、如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2 cm,OA=60 cm,OB=15 cm,则火焰的长度为________.
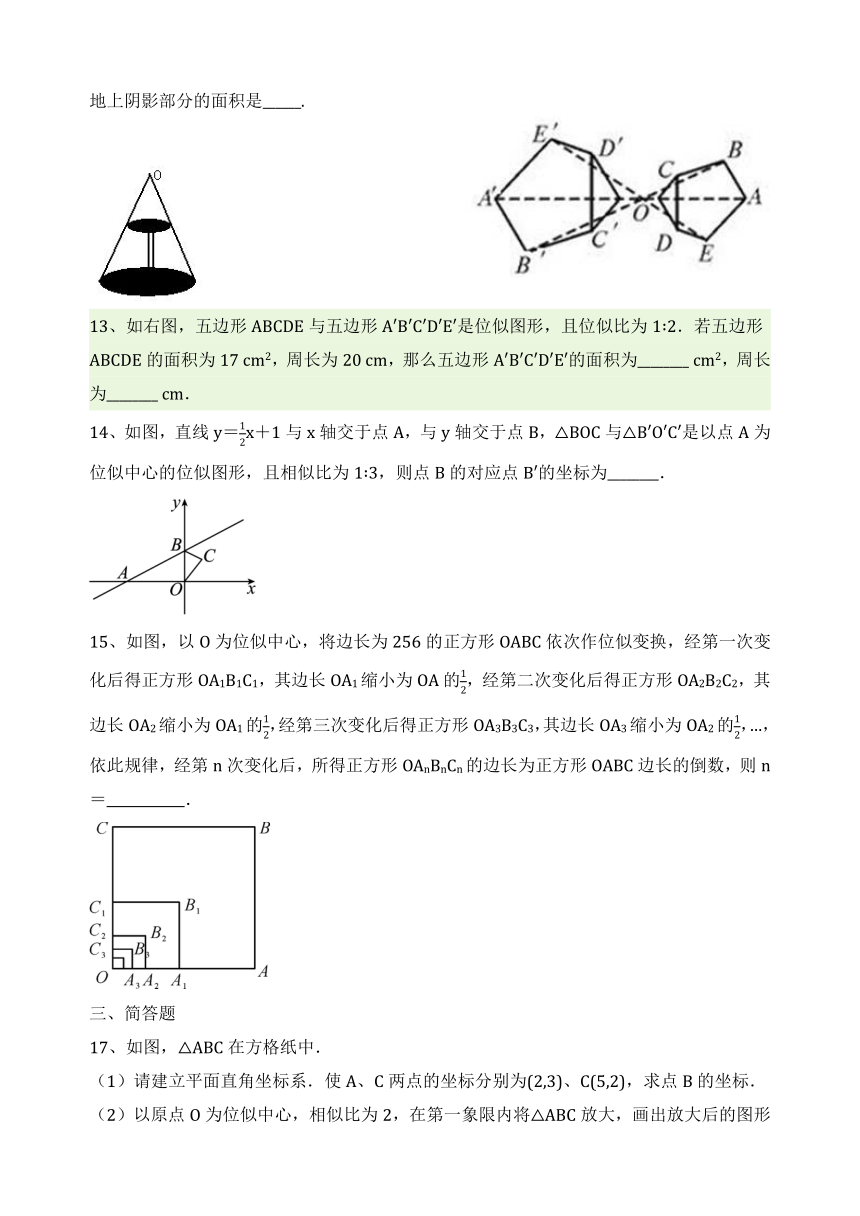
12、如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地上形成阴影(圆形)的示意图,已知桌面的直径为1.2米,桌面距地面1米,灯泡距地面3米,则地上阴影部分的面积是______.
13、如右图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,且位似比为1∶2.若五边形ABCDE的面积为17 cm2,周长为20 cm,那么五边形A′B′C′D′E′的面积为________ cm2,周长为________ cm.
14、如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1∶3,则点B的对应点B′的坐标为________.
15、如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的,…,依此规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n= .
三、简答题
17、如图,△ABC在方格纸中.
(1)请建立平面直角坐标系.使A、C两点的坐标分别为(2,3)、C(5,2),求点B的坐标.
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′.
(3)计算△A′B′C′的面积S.
18、如图,矩形ABCD与矩形AB′C′D′是位似图形,点A为位似中心,已知矩形ABCD的周长为24,BB′=4,DD′=2,求AB,AD的长.
19、如图,矩形ABCD为台球桌面,AD=260 cm,AB=130 cm.球目前在E点位置,AE=60 cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点的位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
20、如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(7,1),B(8,2),C(9,0).
(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形(要求与△ABC同在P点一侧);
(2)求线段BC的对应线段B′C′所在直线的解析式.
21、如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,求点B的横坐标.
答案解析
一、选择题
1-5:ADCAD 6-10:BCBCD
二、填空题
11、8cm; 12、0.81πm2; 13、68;40; 14、(-8,-3),(4,3); 15、16;
三、简答题
17、解:(1)如图画出原点O,x轴、y轴,建立直角坐标系,
可知B的坐标为(2,1);
(2)如(1)中图,画出图形△A′B′C′,即为所求;
(3)S△A′B′C′=×4×6=12.
18、解:∵矩形ABCD的周长为24,
∴AB+AD=12.设AB=x,
则AD=12-x,AB′=x+4,AD′=14-x.
∵矩形ABCD与矩形AB′C′D′是位似图形,
∴=,
即=,
解得x=8,
∴AB=8,AD=12-8=4.
19、解:(1)证明:由题意,得∠EFG=∠DFG.
∵∠EFG+∠BFE=90°,∠DFG+∠CFD=90°,
∴∠BFE=∠CFD.
又∵∠B=∠C=90°,
∴△BEF∽△CDF.
(2)∵△BEF∽△CDF,∴=,
即=.∴CF=169 cm.
20、解:(1)如图所示.
(2)作BD⊥x轴,B′E⊥x轴,垂直分别是D,E点,
∴B′E∥BD.
∴△B′EP∽△BDP.∴==.
∵B(8,2),P(12,0),∴OD=8,BD=2,OP=12.
∴PD=OP-OD=12-8=4.
∵△A′B′C′与△ABC的相似比为3,
∴=3.∴==3.
∴B′E=6,PE=12.
∵PO=12,∴E与O点重合,线段B′E在y轴上.
∴B′点坐标为(0,6).
同理PC′∶PC=3∶1,
又∵PC=OP-OC=12-9=3,∴PC′=9.
∴OC′=12-9=3.∴C′点坐标为(3,0).
设线段B′C′所在直线的解析式为y=kx+b,则
解得
∴线段B′C′所在直线的解析式为y=-2x+6.
21、解:过B′作B′F⊥x轴于点F,过B作BE⊥x轴于点E,则∠BEC=∠B′FC=90°.
又∵∠BCE=∠B′CF,
∴△BEC∽△B′FC.
∴=.
∵△ABC∽△A′B′C,且相似比为,
∴==.
∵点B′的横坐标是a,点C的坐标是(-1,0),
∴FO=a,CO=1.∴FC=a+1.
∴EC=(a+1).
∴点B的横坐标是:-(a+1)-1=-(a+3).
第 页,共 页
试题资源网-凸飞教育科技(北京)有限公司
一、选择题
1、如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为13,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点的坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
2、视力表的一部分如图,其中开口向上的两个“E”之间的变换是( )
A.平移 B.旋转 C.对称 D.位似
3、在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2).若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为( )
A.(5,1) B.(4,3) C.(3,4) D.(1,5)
4、如图,四边形ABCD和是以点O为位似中心的位似图形,若OA::3,则四边形ABCD与四边形的面积比为( )
A. 4:9 B. 2:5 C. 2:3 D. :
5、如图,在平面直角坐标系中,有两点A(4,2),B(3,0),以原点O为位似中心,A′B′与AB的相似比为,得到线段A′B′,正确的画法是( )
A B C D
6、如图,△ABC与△DEF是位似图形,相似比为2∶3,已知AB=4,则DE的长等于( )
A.5 B.6 C.9 D.
7、按如下方法,将的三边缩小的原来的,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得,则下列说法正确的个数是( )
与是位似图形 与是相似图形
与的周长比为1:2 与的面积比为4:1.
A. 1 B. 2 C. 3 D. 4
8、如图,以点A为位似中心,将△ADE放大2倍后,得位似图形△ABC,若S1表示△A DE的面积,S2表示四边形DBCE的面积,则S1∶ S2=( ).
A.1∶2 B.1∶3 C.1∶4 D. 2∶3
9、如图,“小鱼”与“大鱼”是位似图形,已知“小鱼”上一个“顶点”的坐标为(a,b),那么“大鱼”上对应“顶点”的坐标为( )
A.(-a,-2b) B.(-2a,-b)
C.(-2a,-2b) D.(-2b,-2a)
10、如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(-1,2) B.(-9,18)
C.(-9,18)或(9,-18) D.(-1,2)或(1,-2)
二、填空题
11、如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2 cm,OA=60 cm,OB=15 cm,则火焰的长度为________.
12、如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地上形成阴影(圆形)的示意图,已知桌面的直径为1.2米,桌面距地面1米,灯泡距地面3米,则地上阴影部分的面积是______.
13、如右图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,且位似比为1∶2.若五边形ABCDE的面积为17 cm2,周长为20 cm,那么五边形A′B′C′D′E′的面积为________ cm2,周长为________ cm.
14、如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1∶3,则点B的对应点B′的坐标为________.
15、如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的,…,依此规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n= .
三、简答题
17、如图,△ABC在方格纸中.
(1)请建立平面直角坐标系.使A、C两点的坐标分别为(2,3)、C(5,2),求点B的坐标.
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′.
(3)计算△A′B′C′的面积S.
18、如图,矩形ABCD与矩形AB′C′D′是位似图形,点A为位似中心,已知矩形ABCD的周长为24,BB′=4,DD′=2,求AB,AD的长.
19、如图,矩形ABCD为台球桌面,AD=260 cm,AB=130 cm.球目前在E点位置,AE=60 cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点的位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
20、如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(7,1),B(8,2),C(9,0).
(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形(要求与△ABC同在P点一侧);
(2)求线段BC的对应线段B′C′所在直线的解析式.
21、如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,求点B的横坐标.
答案解析
一、选择题
1-5:ADCAD 6-10:BCBCD
二、填空题
11、8cm; 12、0.81πm2; 13、68;40; 14、(-8,-3),(4,3); 15、16;
三、简答题
17、解:(1)如图画出原点O,x轴、y轴,建立直角坐标系,
可知B的坐标为(2,1);
(2)如(1)中图,画出图形△A′B′C′,即为所求;
(3)S△A′B′C′=×4×6=12.
18、解:∵矩形ABCD的周长为24,
∴AB+AD=12.设AB=x,
则AD=12-x,AB′=x+4,AD′=14-x.
∵矩形ABCD与矩形AB′C′D′是位似图形,
∴=,
即=,
解得x=8,
∴AB=8,AD=12-8=4.
19、解:(1)证明:由题意,得∠EFG=∠DFG.
∵∠EFG+∠BFE=90°,∠DFG+∠CFD=90°,
∴∠BFE=∠CFD.
又∵∠B=∠C=90°,
∴△BEF∽△CDF.
(2)∵△BEF∽△CDF,∴=,
即=.∴CF=169 cm.
20、解:(1)如图所示.
(2)作BD⊥x轴,B′E⊥x轴,垂直分别是D,E点,
∴B′E∥BD.
∴△B′EP∽△BDP.∴==.
∵B(8,2),P(12,0),∴OD=8,BD=2,OP=12.
∴PD=OP-OD=12-8=4.
∵△A′B′C′与△ABC的相似比为3,
∴=3.∴==3.
∴B′E=6,PE=12.
∵PO=12,∴E与O点重合,线段B′E在y轴上.
∴B′点坐标为(0,6).
同理PC′∶PC=3∶1,
又∵PC=OP-OC=12-9=3,∴PC′=9.
∴OC′=12-9=3.∴C′点坐标为(3,0).
设线段B′C′所在直线的解析式为y=kx+b,则
解得
∴线段B′C′所在直线的解析式为y=-2x+6.
21、解:过B′作B′F⊥x轴于点F,过B作BE⊥x轴于点E,则∠BEC=∠B′FC=90°.
又∵∠BCE=∠B′CF,
∴△BEC∽△B′FC.
∴=.
∵△ABC∽△A′B′C,且相似比为,
∴==.
∵点B′的横坐标是a,点C的坐标是(-1,0),
∴FO=a,CO=1.∴FC=a+1.
∴EC=(a+1).
∴点B的横坐标是:-(a+1)-1=-(a+3).
第 页,共 页
试题资源网-凸飞教育科技(北京)有限公司
