福建省莆田市第八中学人教A版高中数学必修二课件:2.3.3--2.3.4直线与平面、平面与平面垂直的性质(共33张PPT)
文档属性
| 名称 | 福建省莆田市第八中学人教A版高中数学必修二课件:2.3.3--2.3.4直线与平面、平面与平面垂直的性质(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-29 21:39:03 | ||
图片预览





文档简介
课件33张PPT。2.3.3--2.3.4 直线与平面、平面与平面垂直的性质莆田第八中学
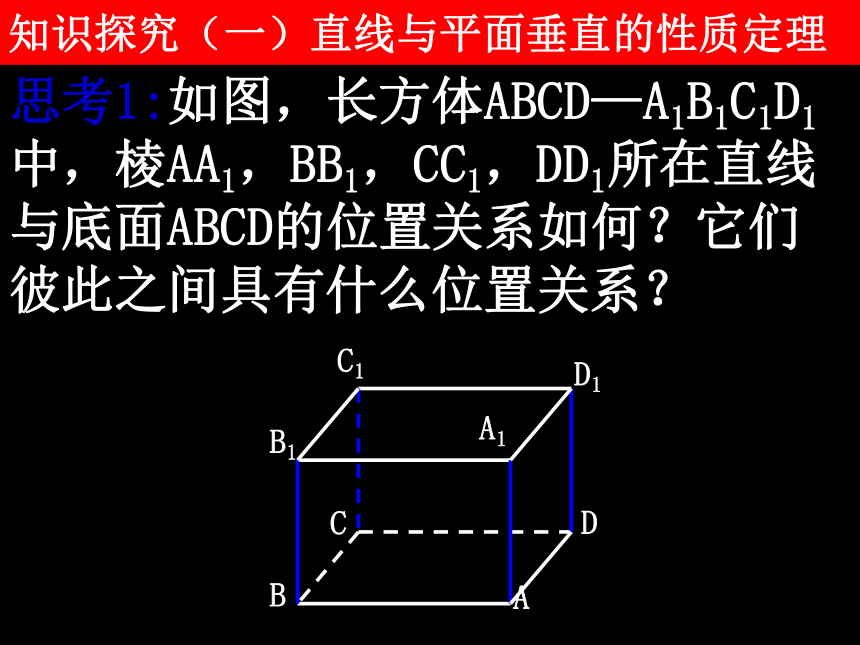
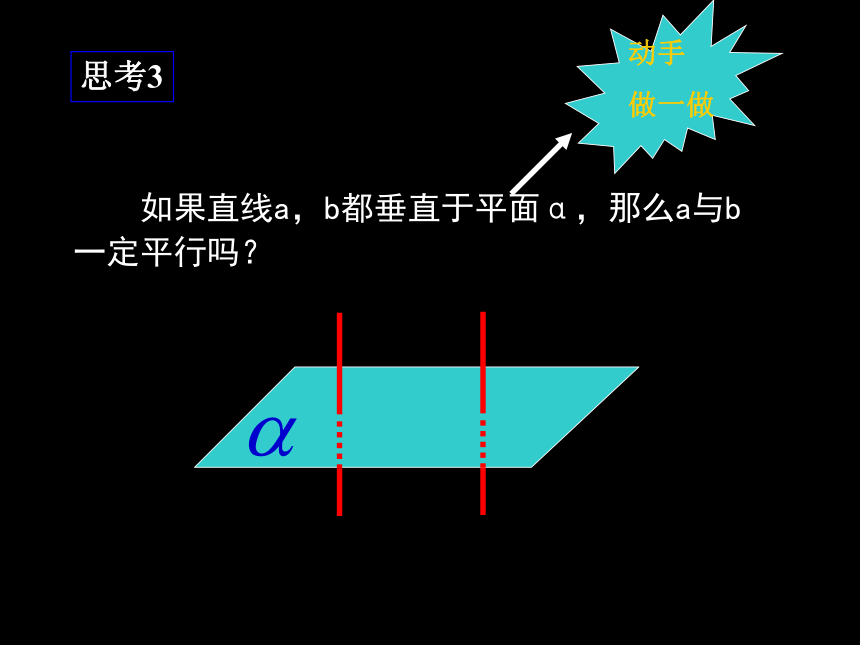
陈梅华大桥的桥柱与水面垂直生活中有很多直线与平面、平面与平面垂直的实例,你能举出几个吗?杭州湾跨海大桥的桥墩与水面垂直知识探究(一)直线与平面垂直的性质定理 思考1:如图,长方体ABCD—A1B1C1D1中,棱AA1,BB1,CC1,DD1所在直线与底面ABCD的位置关系如何?它们彼此之间具有什么位置关系?思考2 如果直线a,b都垂直于同一条直线l,那么直线a,b的位置关系如何?相交平行异面思考3 如果直线a,b都垂直于平面α,那么a与b一定平行吗?动手
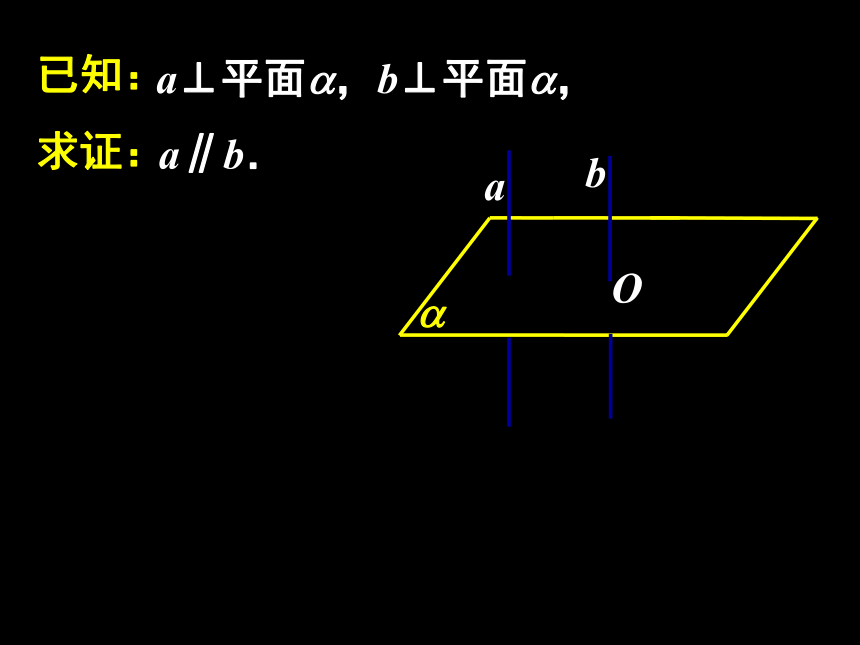
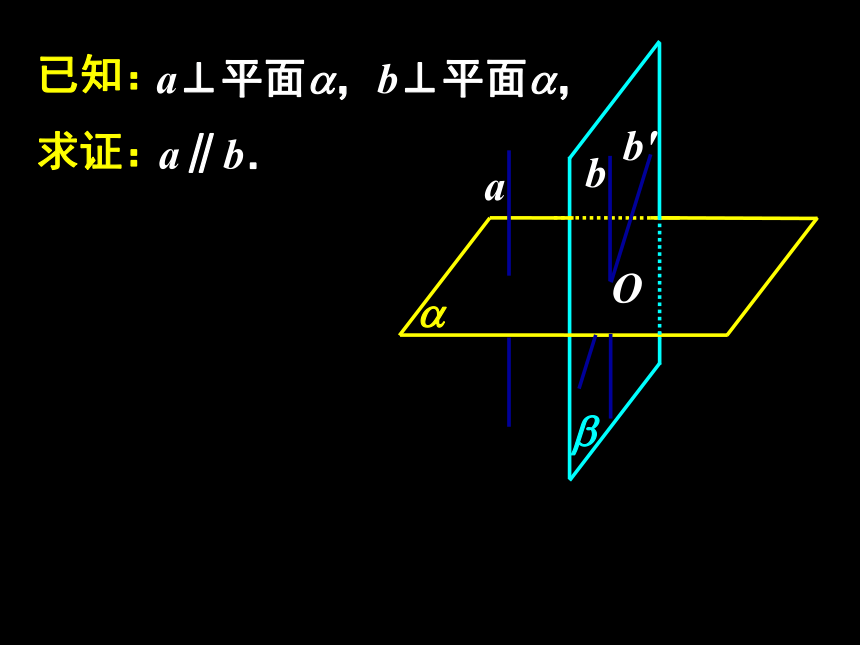
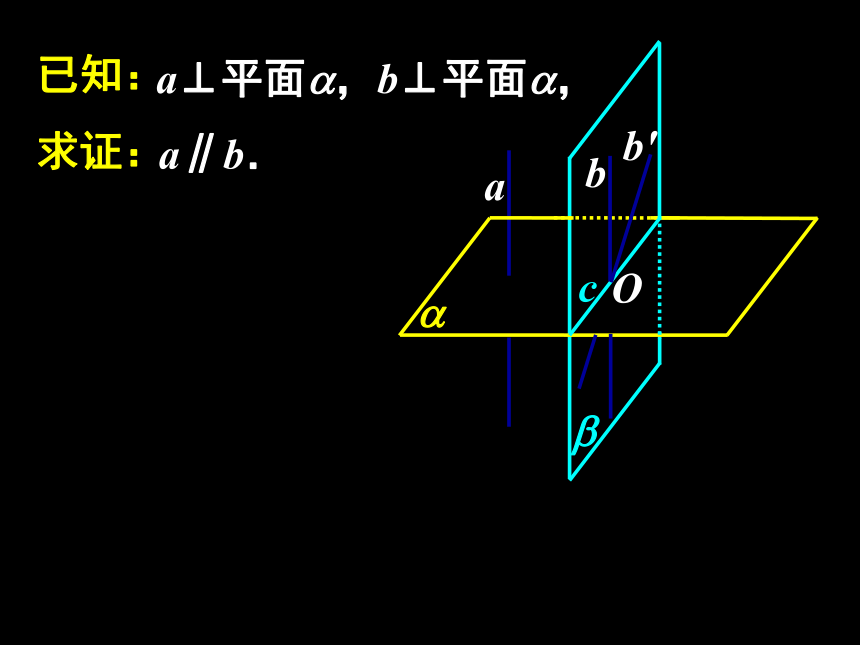
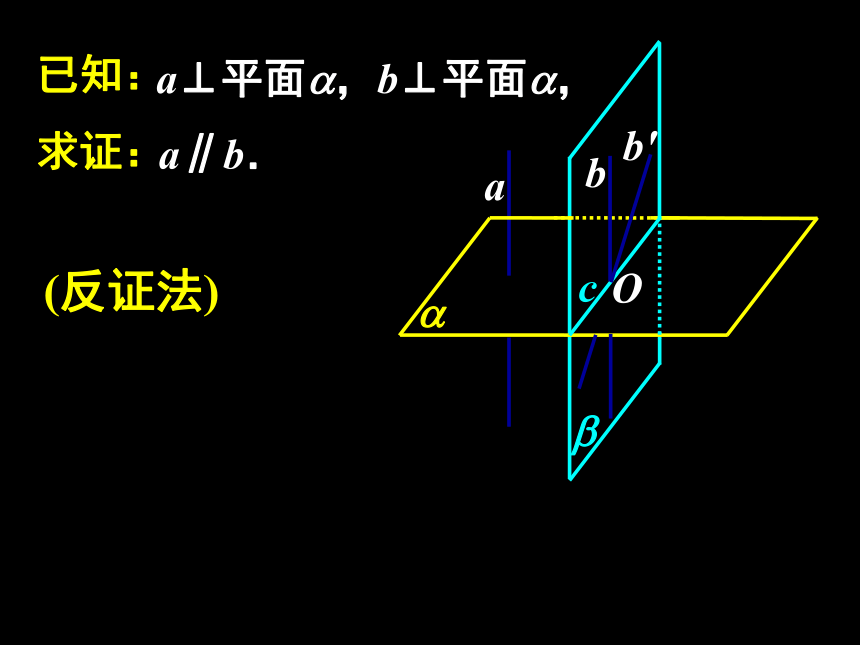
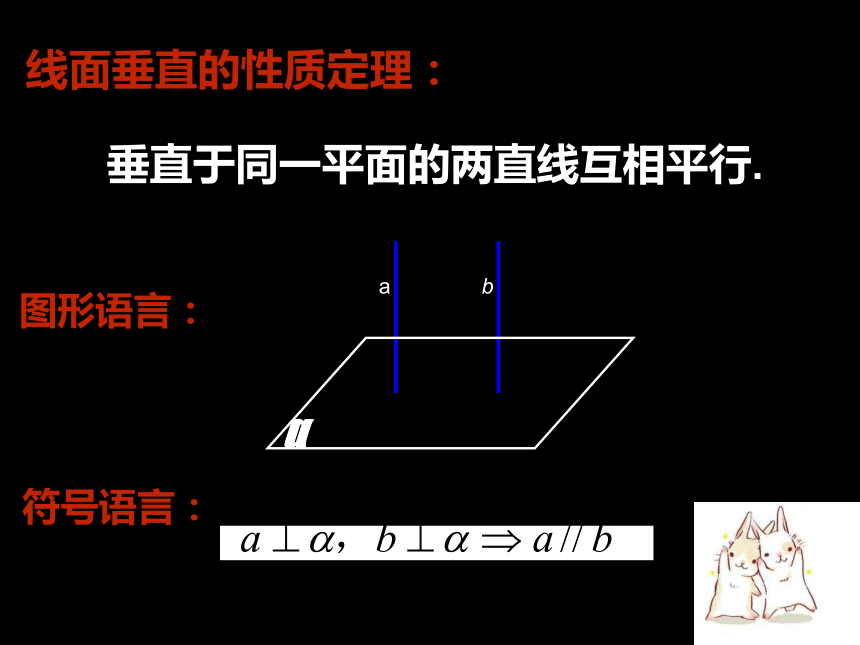
做一做已知:求证:a⊥平面?,b⊥平面?,a∥b.a?bO已知:求证:a⊥平面?,b⊥平面?,a∥b.a?bb'?O已知:求证:a⊥平面?,b⊥平面?,a∥b.a?bb'c?O已知:求证:a⊥平面?,b⊥平面?,a∥b.a?bb'c?O(反证法)线面垂直的性质定理:符号语言:图形语言:垂直于同一平面的两直线互相平行.探究:1、a,b分别在正方体的两个相对面内,此时直线a,b必为这两个面与第三个面的交线2、a,b分别在正方体的两个相邻面内,此时直线a,b必与这两个面的交线平行问题提出 1.平面与平面垂直的定义是什么?如何判定平面与平面垂直? 2.平面与平面垂直的判定定理,解决了两个平面垂直的条件问题;反之,在平面与平面垂直的条件下,能得到哪些结论?定义和判定定理知识探究(二)平面与平面垂直的性质定理 思考1:如果平面α与平面β互相垂直,直线l在平面α内,那么直线l与平面β的位置关系有哪几种可能?知识探究(二)平面与平面垂直的性质定理 思考2:黑板所在平面与地面所在平面垂直,在黑板上是否存在直线与地面垂直?若存在,怎样画线?思考3:如图,长方体ABCD—A1B1C1D1中,平面A1ADD1与平面ABCD垂直,其交线为AD,直线A1A,D1D都在平面A1ADD1内,且都与交线AD垂直,这两条直线与平面ABCD垂直吗?思考5:据上分析可得什么定理?试用文字语言表述之.定理 若两个平面互相垂直,则一个平面内垂直于交线的直线与另一个平面垂直.思考6:上述定理通常叫做两平面垂直的性质定理,结合下图,如何用符号语言描述这个定理?该定理在实际应用中有何理论作用?知识探究(二)平面与平面垂直的性质探究 思考1:若α⊥β,过平面α内一点A作平面β的垂线,垂足为B,那么点B在什么位置?说明你的理由.思考2:上述分析表明:如果两个平面互相垂直,那么经过一个平面内一点且垂直于另一个平面的直线,必在这个平面内.该性质在实际应用中有何理论作用?思考4:上述结论如何用文字语言表述?该性质在实际应用中有何理论作用?如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.理论迁移m例1、如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC
求证: MN∥AD1
典型例题例2:如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC,(2)判断平面PBC与平面PAC的位置关系。(1)判断BC与平面PAC的位置关系,并证明。练习练习2:如图,已知PA⊥平面ABC,
平面PAB⊥平面PBC,求证:BC⊥平面PABE练习3:如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,求BD与平面ABC所成的角。ABCDDABCOO折成小结线线垂直线面垂直面面垂直线线平行面面平行作业:
P73练习:1,2.(做书上)
P73习题2.3A组:2,5 ,8
P74习题2.3B组:3.谢谢各位的光临指导!
陈梅华大桥的桥柱与水面垂直生活中有很多直线与平面、平面与平面垂直的实例,你能举出几个吗?杭州湾跨海大桥的桥墩与水面垂直知识探究(一)直线与平面垂直的性质定理 思考1:如图,长方体ABCD—A1B1C1D1中,棱AA1,BB1,CC1,DD1所在直线与底面ABCD的位置关系如何?它们彼此之间具有什么位置关系?思考2 如果直线a,b都垂直于同一条直线l,那么直线a,b的位置关系如何?相交平行异面思考3 如果直线a,b都垂直于平面α,那么a与b一定平行吗?动手
做一做已知:求证:a⊥平面?,b⊥平面?,a∥b.a?bO已知:求证:a⊥平面?,b⊥平面?,a∥b.a?bb'?O已知:求证:a⊥平面?,b⊥平面?,a∥b.a?bb'c?O已知:求证:a⊥平面?,b⊥平面?,a∥b.a?bb'c?O(反证法)线面垂直的性质定理:符号语言:图形语言:垂直于同一平面的两直线互相平行.探究:1、a,b分别在正方体的两个相对面内,此时直线a,b必为这两个面与第三个面的交线2、a,b分别在正方体的两个相邻面内,此时直线a,b必与这两个面的交线平行问题提出 1.平面与平面垂直的定义是什么?如何判定平面与平面垂直? 2.平面与平面垂直的判定定理,解决了两个平面垂直的条件问题;反之,在平面与平面垂直的条件下,能得到哪些结论?定义和判定定理知识探究(二)平面与平面垂直的性质定理 思考1:如果平面α与平面β互相垂直,直线l在平面α内,那么直线l与平面β的位置关系有哪几种可能?知识探究(二)平面与平面垂直的性质定理 思考2:黑板所在平面与地面所在平面垂直,在黑板上是否存在直线与地面垂直?若存在,怎样画线?思考3:如图,长方体ABCD—A1B1C1D1中,平面A1ADD1与平面ABCD垂直,其交线为AD,直线A1A,D1D都在平面A1ADD1内,且都与交线AD垂直,这两条直线与平面ABCD垂直吗?思考5:据上分析可得什么定理?试用文字语言表述之.定理 若两个平面互相垂直,则一个平面内垂直于交线的直线与另一个平面垂直.思考6:上述定理通常叫做两平面垂直的性质定理,结合下图,如何用符号语言描述这个定理?该定理在实际应用中有何理论作用?知识探究(二)平面与平面垂直的性质探究 思考1:若α⊥β,过平面α内一点A作平面β的垂线,垂足为B,那么点B在什么位置?说明你的理由.思考2:上述分析表明:如果两个平面互相垂直,那么经过一个平面内一点且垂直于另一个平面的直线,必在这个平面内.该性质在实际应用中有何理论作用?思考4:上述结论如何用文字语言表述?该性质在实际应用中有何理论作用?如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.理论迁移m例1、如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC
求证: MN∥AD1
典型例题例2:如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC,(2)判断平面PBC与平面PAC的位置关系。(1)判断BC与平面PAC的位置关系,并证明。练习练习2:如图,已知PA⊥平面ABC,
平面PAB⊥平面PBC,求证:BC⊥平面PABE练习3:如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,求BD与平面ABC所成的角。ABCDDABCOO折成小结线线垂直线面垂直面面垂直线线平行面面平行作业:
P73练习:1,2.(做书上)
P73习题2.3A组:2,5 ,8
P74习题2.3B组:3.谢谢各位的光临指导!
