【满分备考】通用版小学数学小升初复习学案3——数式和数形综合(含答案)
文档属性
| 名称 | 【满分备考】通用版小学数学小升初复习学案3——数式和数形综合(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 08:14:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【命题猜想3】数式和数形综合——定义新运算与规律探索。
【命题说明】
定义新运算是指运用某种特殊符号来表示特定的意义,从而解答某些算式的一种运算,它是一种人为的、临时性的运算形式,它使用的是一些特殊的运算符号,如:*、△、⊙等,这是与四则运算中的“+、-、×、÷”不同的。
小升初中的新运算考察形式较为简单,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。21世纪教育网版权所有
数形规律也是常考察题型之一,主要以数字数列、图形图表、算式等形式为主,考点和题型探索性和抽象性较强,一般学生解决起来稍显吃力,可着重进行强化训练。21教育网
【预测命题1】定义新运算。
例题:(2023·南京市小升初真题)对于两个数a与b,规定aθb=a×b+a+b。
(1)求6θ2;2θ6;
(2)求(17θ6)θ2;17θ(6θ2);
(3)这个运算θ有交换律和结合律吗?
解析:
【答案】(1)20;20;
(2)377;377
(3)θ有交换律和结合律。
【分析】第一、第二小题,根据给出的式子得出新的运算方法是:将运算符号的前后两个先相乘再相加,由此解答。
第三小题,根据交换律和结合律的意义,验证θ具有交换律和结合律即可。
【详解】(1)6θ2
=6×2+6+2
=12+6+2
=20
2θ6
=2×6+2+6
=12+2+6
=20
(2)(17θ6)θ2
=(17×6+17+6)θ2
=(102+17+6)θ2
=125θ2
=125×2+125+2
=250+125+2
=377
17θ(6θ2)
=17θ(6×2+6+2)
=17θ(12+6+2)
=17θ20
=17×20+17+20
=340+17+20
=377
(3)aθb
=a×b+a+b
=b×a+b+a
所以,aθb=bθa,即θ满足交换律。
(aθb)θc
=(a×b+a+b)θc
=(a×b+a+b)×c+a×b+a+b+c
=a×b×c+a×c+b×c+a×b+a+b+c
aθ(bθc)
=aθ(b×c+b+c)
=a×(b×c+b+c)+b×c+b+c
=a×b×c+a×c+b×c+a×b+a+b+c
所以,(aθb)θc= aθ(bθc),即θ具有结合律。
答:θ有交换律和结合律。
【点睛】关键是根据给出的式子,得出新的运算方法,再利用新的运算方法解决问题。
【真题练习】
1.(2023·长沙市小升初真题)对两个整数和定义新运算“”:,求。
2.(2023·成都市小升初真题)规定,,,,……如果,那么是几?
3.(2023·浏阳市小升初真题)规定“”为一种新运算,对于任意两个数和都有,如果,已知,求的值。
【预测命题2】数形规律。
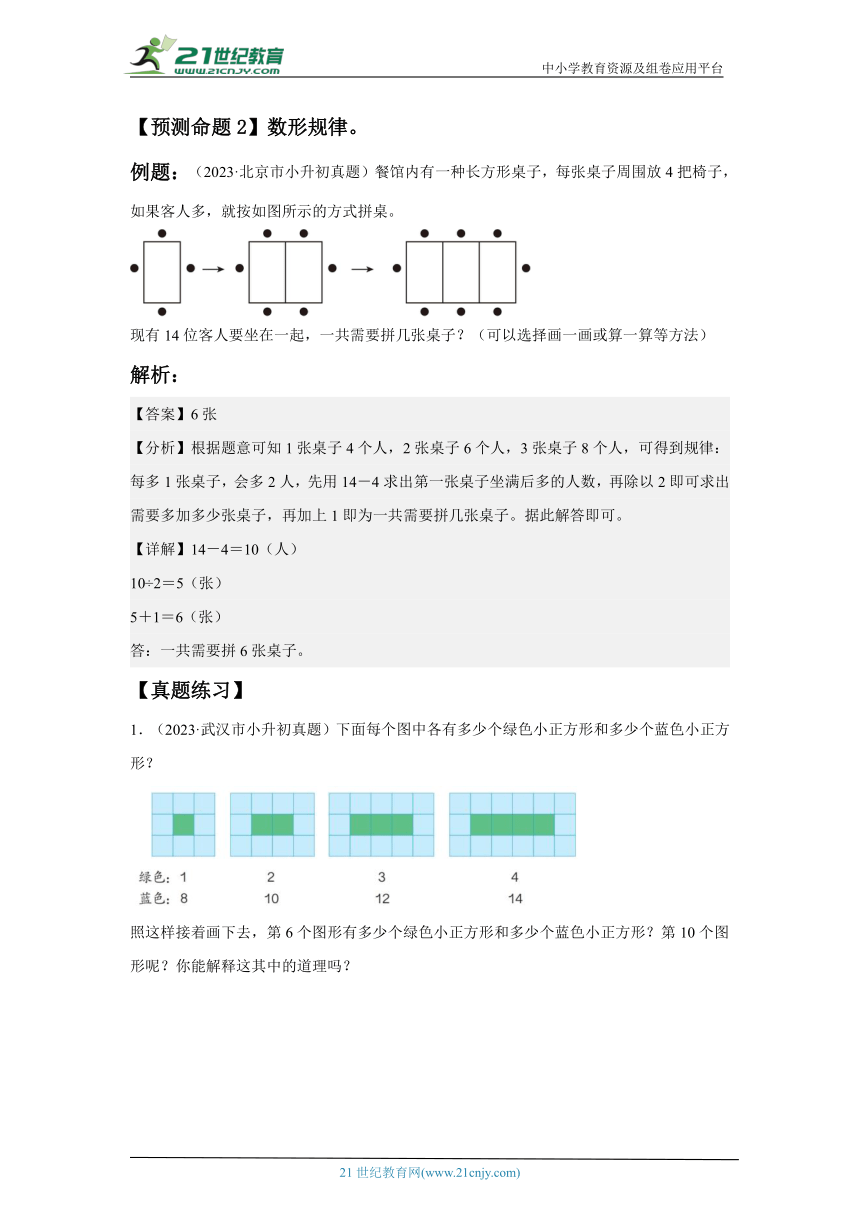
例题:(2023·北京市小升初真题)餐馆内有一种长方形桌子,每张桌子周围放4把椅子,如果客人多,就按如图所示的方式拼桌。
现有14位客人要坐在一起,一共需要拼几张桌子?(可以选择画一画或算一算等方法)
解析:
【答案】6张
【分析】根据题意可知1张桌子4个人,2张桌子6个人,3张桌子8个人,可得到规律:每多1张桌子,会多2人,先用14-4求出第一张桌子坐满后多的人数,再除以2即可求出需要多加多少张桌子,再加上1即为一共需要拼几张桌子。据此解答即可。
【详解】14-4=10(人)
10÷2=5(张)
5+1=6(张)
答:一共需要拼6张桌子。
【真题练习】
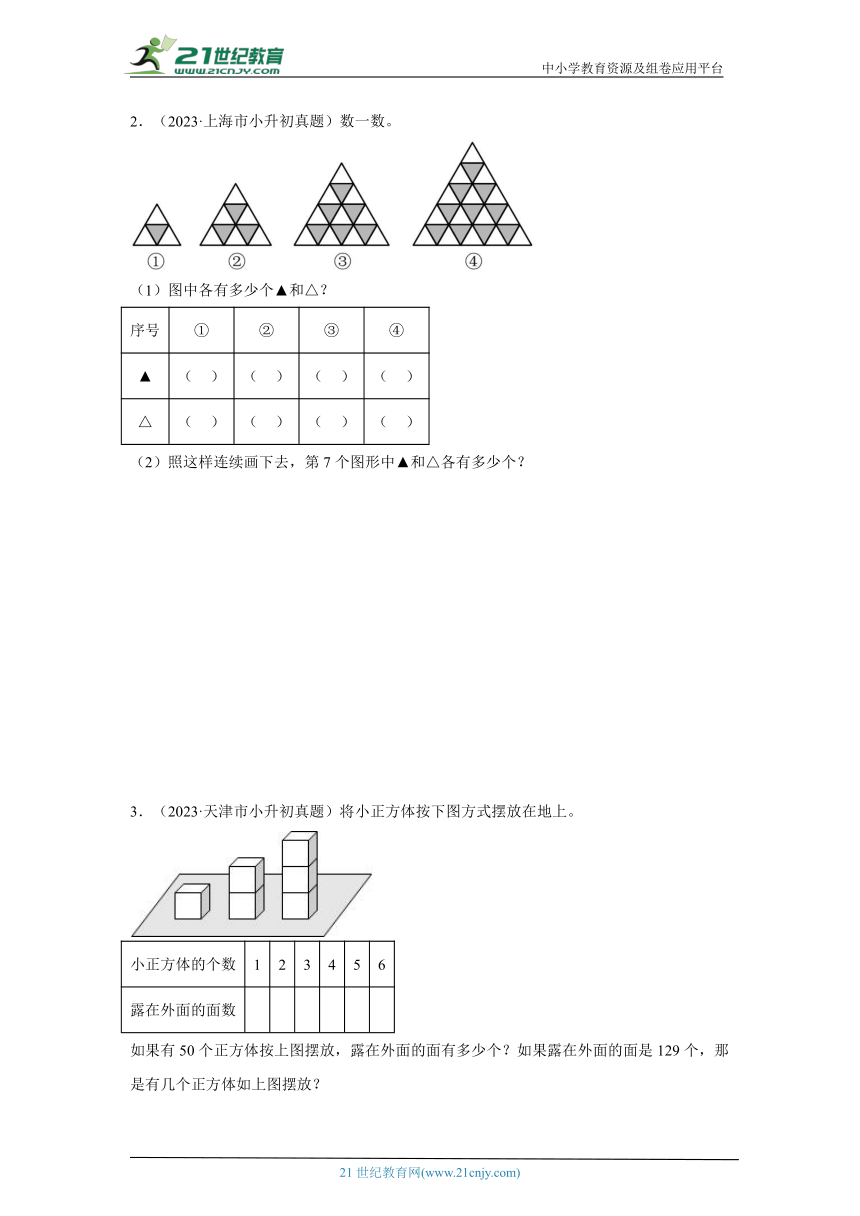
1.(2023·武汉市小升初真题)下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形?
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
2.(2023·上海市小升初真题)数一数。
(1)图中各有多少个▲和△?
序号 ① ② ③ ④
▲ ( ) ( ) ( ) ( )
△ ( ) ( ) ( ) ( )
(2)照这样连续画下去,第7个图形中▲和△各有多少个?
3.(2023·天津市小升初真题)将小正方体按下图方式摆放在地上。
小正方体的个数 1 2 3 4 5 6
露在外面的面数
如果有50个正方体按上图摆放,露在外面的面有多少个?如果露在外面的面是129个,那是有几个正方体如上图摆放?
【预测命题3】数式规律。
例题:(2023·溧阳市小升初真题)三千多年前,埃及人发明了一种记录分数的方法,这些分数的分子为1,它们被称为“单位分数”,通过研究,小明发现一些分数可以很容易地拆分为两个不同的“单位分数”之和(或差)例如:
,;
,;
(1)请根据上述拆分方法将下列分数拆分为“单位分数”的和或差:
= ;= ;
(2)请运用上述拆分方法计算:。
解析:
【答案】(1);
(2)
【分析】(1)观察算式可知,若该分数的分子不是1,则把分数的分母拆成相邻的两个自然数的乘积形式,分子是这两个自然数和的形式,进而写成分母是两个数的乘积形式,分子分别是这两个数,再化简成分子为1的分数形式;若该分数的分子是1,则把分数的分母拆成相邻的两个自然数的乘积形式,分子是这两个自然数差的形式,而写成分母是两个数的乘积形式,分子分别是这两个数,再化简成分子为1的分数形式;
(2) 根据(1)中发现的规律,把算式中的每个分数进行拆分,去括号后,再运用加法结合律进行计算即可。
【详解】(1)=;=;
(2)
=
=
=
=
=
=
=
【点睛】本题主要考查算式的规律,数字的变化类,解答的关键是理解清楚所给的规律并灵活运用。
【真题练习】
1.(2023·无锡市小升初真题)探索与发现:奇思在乘法口诀表上发现一组有趣的算式,如:
6×6=36
5×7=35
4×8=32
3×9=27
(1)根据上面这组乘法算式的特点,在上面右边横线上再写一组这样的算式。
(2)观察上述这两组算式,你发现乘数怎样变化会引起积怎样变化?
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是( )。
A.(a+1)×(a-1)=a2+1
B.(a+1)×(a-1)=a2
C.(a+1)×(a-1)=a2-1
D.(a+2)×(a-2)=a2+2
(4)根据上面发现的规律,如果2022×2022=4088484,则2021×2023=( )。
2.(2023·青岛市小升初真题)先找规律再填空。(图中阴影表示每次截去后剩下的部分)
第四次截去后剩下,第( )次截去后剩下。
【预测命题4】数列规律。
例题:(2023·湘潭市小升初真题)已知一列数按294736294736294……排列,那么前40个数字之和是多少?
解析:
【答案】208
【分析】294736294736294……这一列数字是按照2、9、4、7、3、6这6个数字为一组进行循环出现的,求出40里面有多少个这样的一组,还余几;求出每组和,进而求出前40个数字的和。
【详解】2、9、4、7、3、6这6个数字为一组进行循环出现
2+9+4+7+3+6=31
40÷6=6(组)…4(个)
6组还余4个数字,余下的4个是2,9,4,7
2+9+4+7=22
31×6+22=208
答:前40个数字之和是208。
【点睛】解决这类问题往往是把重复出现的部分看成一组,先找出排列的周期性规律,再根据规律求解。
【真题练习】
1.(2023·株洲市小升初真题)丁丁也不甘示弱:你们知道著名的“斐波那契”数列吗?它是这样一组数:1,1,2,3,5,8,13,21,……从第三个数开始,以后每个数都是它前两个数的和,请问:前2016个数中共有多少个偶数?
2.(2023·徐州市小升初真题)(1)用一个长方形像图中那样任意圈出四个数字,你发现了什么规律?
(2)如果长方形中最上面一个数字用表示,最下面一个数字可以怎样表示?
(3)按这样的圈法,小丽圈出的四个数的和是200,你知道她圈的是哪四个数吗?算一算写出来。
3.(2023·重庆市小升初真题)有下面一串分数:;,,;,,,,;,,,,,,……
(1)是第几个分数?
(2)第400个分数是几分之几?
【命题猜想3】数式和数形综合——定义新运算与规律探索。
【命题说明】
定义新运算是指运用某种特殊符号来表示特定的意义,从而解答某些算式的一种运算,它是一种人为的、临时性的运算形式,它使用的是一些特殊的运算符号,如:*、△、⊙等,这是与四则运算中的“+、-、×、÷”不同的。
小升初中的新运算考察形式较为简单,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。21世纪教育网版权所有
数形规律也是常考察题型之一,主要以数字数列、图形图表、算式等形式为主,考点和题型探索性和抽象性较强,一般学生解决起来稍显吃力,可着重进行强化训练。21教育网
【预测命题1】定义新运算。
例题:(2023·南京市小升初真题)对于两个数a与b,规定aθb=a×b+a+b。
(1)求6θ2;2θ6;
(2)求(17θ6)θ2;17θ(6θ2);
(3)这个运算θ有交换律和结合律吗?
解析:
【答案】(1)20;20;
(2)377;377
(3)θ有交换律和结合律。
【分析】第一、第二小题,根据给出的式子得出新的运算方法是:将运算符号的前后两个先相乘再相加,由此解答。
第三小题,根据交换律和结合律的意义,验证θ具有交换律和结合律即可。
【详解】(1)6θ2
=6×2+6+2
=12+6+2
=20
2θ6
=2×6+2+6
=12+2+6
=20
(2)(17θ6)θ2
=(17×6+17+6)θ2
=(102+17+6)θ2
=125θ2
=125×2+125+2
=250+125+2
=377
17θ(6θ2)
=17θ(6×2+6+2)
=17θ(12+6+2)
=17θ20
=17×20+17+20
=340+17+20
=377
(3)aθb
=a×b+a+b
=b×a+b+a
所以,aθb=bθa,即θ满足交换律。
(aθb)θc
=(a×b+a+b)θc
=(a×b+a+b)×c+a×b+a+b+c
=a×b×c+a×c+b×c+a×b+a+b+c
aθ(bθc)
=aθ(b×c+b+c)
=a×(b×c+b+c)+b×c+b+c
=a×b×c+a×c+b×c+a×b+a+b+c
所以,(aθb)θc= aθ(bθc),即θ具有结合律。
答:θ有交换律和结合律。
【点睛】关键是根据给出的式子,得出新的运算方法,再利用新的运算方法解决问题。
【真题练习】
1.(2023·长沙市小升初真题)对两个整数和定义新运算“”:,求。
【答案】
【分析】由可知:定义新运算“”的意义是:分子是前面数的2倍减去后面的数,分母是前面数加后面数的和乘前面数减后面数的差,代入数据计算即可。
【详解】
=+
=+
=
【点睛】解答此类问题,关键是要正确理解新定义的算式含义,严格按照定义新运算的计算程序将数值代入,转化为常规的四则运算算式进行计算。
2.(2023·成都市小升初真题)规定,,,,……如果,那么是几?
【答案】
【分析】将化为:再根据等式的性质进行解答即可。
【详解】由,可得:
进而得出
根据等式的性质2得:A+1=÷,将=5×6×7,=6×7×8代入可得:
A+1=÷
所以A=-1=
答:是。
【点睛】本题是一道稍复杂的等量代换,合理运用等式的性质是解题的关键。
3.(2023·浏阳市小升初真题)规定“”为一种新运算,对于任意两个数和都有,如果,已知,求的值。
【答案】x=
【分析】根据题中的新定义计算即可。
【详解】根据题中的新定义可得:+=5
解方程可得x=
答:的值是。
【点睛】本题是一道定义新运算问题,解题的关键是正确理解定义的运算符号的意义。
【预测命题2】数形规律。
例题:(2023·北京市小升初真题)餐馆内有一种长方形桌子,每张桌子周围放4把椅子,如果客人多,就按如图所示的方式拼桌。
现有14位客人要坐在一起,一共需要拼几张桌子?(可以选择画一画或算一算等方法)
解析:
【答案】6张
【分析】根据题意可知1张桌子4个人,2张桌子6个人,3张桌子8个人,可得到规律:每多1张桌子,会多2人,先用14-4求出第一张桌子坐满后多的人数,再除以2即可求出需要多加多少张桌子,再加上1即为一共需要拼几张桌子。据此解答即可。
【详解】14-4=10(人)
10÷2=5(张)
5+1=6(张)
答:一共需要拼6张桌子。
【真题练习】
1.(2023·武汉市小升初真题)下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形?
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
【答案】绿色6个;蓝色18个;绿色10个;蓝色26个;见详解
【分析】第1个图形,有1个绿色小正方形,8个蓝色小正方形,8=2×1+6;
第2个图形,有2个绿色小正方形,10个蓝色小正方形,10=2×2+6;
第3个图形,有3个绿色小正方形,12个蓝色小正方形,12=2×3+6;
第4个图形,有4个绿色小正方形,14个蓝色小正方形,14=2×4+6;
……
规律:第n个图形,有n个绿色小正方形,(2n+6)个蓝色小正方形;据此解答。
【详解】规律:第n个图形,有n个绿色小正方形,(2n+6)个蓝色小正方形。
当n=6时,有6个绿色小正方形;
蓝色小正方形有:
2n+6
=2×6+6
=12+6
=18(个)
当n=10时,有10个绿色小正方形;
蓝色小正方形有:
2n+6
=2×10+6
=20+6
=26(个)
答:照这样接着画下去,第6个图形有6个绿色小正方形和18个蓝色小正方形。第10个图形有10个绿色小正方形和26个蓝色小正方形。
道理:从图中发现规律:第n个图形有n个绿色小正方形,(2n+6)个蓝色小正方形。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
2.(2023·上海市小升初真题)数一数。
(1)图中各有多少个▲和△?
序号 ① ② ③ ④
▲ ( ) ( ) ( ) ( )
△ ( ) ( ) ( ) ( )
(2)照这样连续画下去,第7个图形中▲和△各有多少个?
【答案】(1)1;3;6;10
3;6;10;15
(2)▲有28个;△有36个
【分析】第1个图有1个▲,第2个图有1+2=3(个)▲,第3个图有1+2+3=6(个)▲,第4个图有1+2+3+4=10(个)▲,……由此发现规律:第n图有(1+2+3+4+…+n)个▲。
第1个图有1+2=3(个)△,第2个图有1+2+3=6(个)△,第3个图有1+2+3+4=10(个)△,第4个图有1+2+3+4+5=15(个)△……由此发现规律:第n图有[1+2+3+4+…+(n+1)]个△。
【详解】(1)▲的个数:
第1个图:1个
第2个图:1+2=3(个)
第3个图:1+2+3=6(个)
第4个图:1+2+3+4=10(个)
△的个数:
第1个图:1+2=3(个)
第2个图:1+2+3=6(个)
第3个图:1+2+3+4=10(个)
第4个图:1+2+3+4+5=15(个)
如下表:
序号 ① ② ③ ④
▲ 1 3 6 10
△ 3 6 10 15
(2)1+2+3+4+5+6+7=28(个)
1+2+3+4+5+6+7+8=36(个)
答:第7个图形中▲有28个,△各有36个。
【点睛】在运用数形结合的方法探究数学规律时,一定要把图形和数一一对应。
3.(2023·天津市小升初真题)将小正方体按下图方式摆放在地上。
小正方体的个数 1 2 3 4 5 6
露在外面的面数
如果有50个正方体按上图摆放,露在外面的面有多少个?如果露在外面的面是129个,那是有几个正方体如上图摆放?
【答案】表格见详解;201个;32个
【分析】由题意可知,有1个小正方体露在外面的面数有5面,2个小正方体露在外面的面数有9个,3个小正方体露在外面的面数有13个,则有n个正方体,则露在外面的面有(4n+1)个,据此解答即可。
【详解】当n=4时
4n+1=4×4+1
=16+1
=17(个)
当n=5时
4n+1=4×5+1
=20+1
=21(个)
当n=6时
4n+1=4×6+1
=24+1
=25(个)
当n=50时
4n+1=4×50+1
=200+1
=201(个)
解:设如果露在外面的面是129个,那是有x个正方体如上图摆放。
4n+1=129
4n+1-1=129-1
4n=128
4n÷4=128÷4
n=32
则如果有50个正方体按上图摆放,露在外面的面有201个,如果露在外面的面是129个,那是有32个正方体如上图摆放。
如图所示:
小正方体的个数 1 2 3 4 5 6
露在外面的面数 5 9 13 17 21 25
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
【预测命题3】数式规律。
例题:(2023·溧阳市小升初真题)三千多年前,埃及人发明了一种记录分数的方法,这些分数的分子为1,它们被称为“单位分数”,通过研究,小明发现一些分数可以很容易地拆分为两个不同的“单位分数”之和(或差)例如:
,;
,;
(1)请根据上述拆分方法将下列分数拆分为“单位分数”的和或差:
= ;= ;
(2)请运用上述拆分方法计算:。
解析:
【答案】(1);
(2)
【分析】(1)观察算式可知,若该分数的分子不是1,则把分数的分母拆成相邻的两个自然数的乘积形式,分子是这两个自然数和的形式,进而写成分母是两个数的乘积形式,分子分别是这两个数,再化简成分子为1的分数形式;若该分数的分子是1,则把分数的分母拆成相邻的两个自然数的乘积形式,分子是这两个自然数差的形式,而写成分母是两个数的乘积形式,分子分别是这两个数,再化简成分子为1的分数形式;
(2) 根据(1)中发现的规律,把算式中的每个分数进行拆分,去括号后,再运用加法结合律进行计算即可。
【详解】(1)=;=;
(2)
=
=
=
=
=
=
=
【点睛】本题主要考查算式的规律,数字的变化类,解答的关键是理解清楚所给的规律并灵活运用。
【真题练习】
1.(2023·无锡市小升初真题)探索与发现:奇思在乘法口诀表上发现一组有趣的算式,如:
6×6=36
5×7=35
4×8=32
3×9=27
(1)根据上面这组乘法算式的特点,在上面右边横线上再写一组这样的算式。
(2)观察上述这两组算式,你发现乘数怎样变化会引起积怎样变化?
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是( )。
A.(a+1)×(a-1)=a2+1
B.(a+1)×(a-1)=a2
C.(a+1)×(a-1)=a2-1
D.(a+2)×(a-2)=a2+2
(4)根据上面发现的规律,如果2022×2022=4088484,则2021×2023=( )。
【答案】(1)7×7=49
6×8=48
5×9=45
4×10=40
(2)两个相同的因数相乘,如果一个因数加n,另一个因数减n,积就等于因数的平方减n2。
(3)C
(4)4088483
【分析】根据算式的规律,可以发现:
6×6和5×7之间的规律可以用字母表示出来:(a+1)×(a-1)=a2-1;
6×6和4×8之间的规律可以用字母表示出来:(a+2)×(a-2)=a2-22;
6×6和3×9之间的规律可以用字母表示出来:(a+3)×(a-3)=a2-32;
据此结合题意解答即可。
【详解】(1)根据上面这组乘法算式的特点,在右边横线上再写一组这样的算式:
7×7=49
6×8=48
5×9=45
4×10=40(答案不唯一)
(2)观察上述这两组算式,发现:两个相同的因数相乘,如果一个因数加n,另一个因数减n,积就等于因数的平方减n2。
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是(a+1)×(a-1)=a2-1
故答案为:C
(4)根据上面发现的规律,如果2022×2022=4088484,则:
2021×2023
=2022×2022-1
=4088484-1
=4088483
【点睛】本题考查了式的规律知识,结合题意分析解答即可。
2.(2023·青岛市小升初真题)先找规律再填空。(图中阴影表示每次截去后剩下的部分)
第四次截去后剩下,第( )次截去后剩下。
【答案】规律:第几次截去后剩下的就用1连续乘几个;16;7
【分析】观察图形可知,每次剩下,第一次1×;第二次1××;第三次1×××,第几次就用1连续乘几个;据此解答。
【详解】规律:第几次截去后剩下的就用1连续乘几个。
1××××
=×××
=××
=×
=
第五次截去后还剩:×=
第六次截去后还剩:×=
第七次截去后还剩:×=
第四次截去后剩下,第7次截去后剩下。
【点睛】在数学算式中探索规律,需要仔细观察算式特点,找出规律,根据规律填出这一类算式的结果。
【预测命题4】数列规律。
例题:(2023·湘潭市小升初真题)已知一列数按294736294736294……排列,那么前40个数字之和是多少?
解析:
【答案】208
【分析】294736294736294……这一列数字是按照2、9、4、7、3、6这6个数字为一组进行循环出现的,求出40里面有多少个这样的一组,还余几;求出每组和,进而求出前40个数字的和。
【详解】2、9、4、7、3、6这6个数字为一组进行循环出现
2+9+4+7+3+6=31
40÷6=6(组)…4(个)
6组还余4个数字,余下的4个是2,9,4,7
2+9+4+7=22
31×6+22=208
答:前40个数字之和是208。
【点睛】解决这类问题往往是把重复出现的部分看成一组,先找出排列的周期性规律,再根据规律求解。
【真题练习】
1.(2023·株洲市小升初真题)丁丁也不甘示弱:你们知道著名的“斐波那契”数列吗?它是这样一组数:1,1,2,3,5,8,13,21,……从第三个数开始,以后每个数都是它前两个数的和,请问:前2016个数中共有多少个偶数?
【答案】672个
【分析】由奇数+奇数=偶数,偶数十奇数=奇数,从而可以发现斐波那契数列中数列是以“奇数、奇数、偶数、奇数、奇数、偶数……”3个一周期排列的,所以2016÷3=672(个)周期,每个周期里有1个偶数,672×1=672(个),即有672个偶数。
【详解】2016÷3=672(个)
672×1=672(个)
答:前2016个数中共有672个偶数。
【点睛】找到题干中的数列规律是解题的关键。
2.(2023·徐州市小升初真题)(1)用一个长方形像图中那样任意圈出四个数字,你发现了什么规律?
(2)如果长方形中最上面一个数字用表示,最下面一个数字可以怎样表示?
(3)按这样的圈法,小丽圈出的四个数的和是200,你知道她圈的是哪四个数吗?算一算写出来。
【答案】(1)每相邻两个之间相差10;
(2);
(3)35、45、55、65。
【分析】(1)观察上下相邻的数之间的大小关系,得出规律;
(2)长方形中一共有4个数,最上面和最下面之间相差30,据此列式;
(3)设小丽圈出的第一个数字为,下面的数依次是a+10、a+20、a+30,根据四个数相加等于200,列出方程,求出第一个数,再分别求出下面的数即可。
【详解】(1)我发现圈出的4个数,每相邻两个之间相差10。
(2)最下面一个数字可以用表示。
(3)解:设小丽圈出的第一个数字为。
4+60=200
4=140
,,。
答:她圈的是35、45、55、65。
【点睛】本题考查了数字的排列规律和列方程解决问题,关键是发现数表中的规律。
3.(2023·重庆市小升初真题)有下面一串分数:;,,;,,,,;,,,,,,……
(1)是第几个分数?
(2)第400个分数是几分之几?
【答案】(1)第88个和第94个 (2)
【详解】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【命题猜想3】数式和数形综合——定义新运算与规律探索。
【命题说明】
定义新运算是指运用某种特殊符号来表示特定的意义,从而解答某些算式的一种运算,它是一种人为的、临时性的运算形式,它使用的是一些特殊的运算符号,如:*、△、⊙等,这是与四则运算中的“+、-、×、÷”不同的。
小升初中的新运算考察形式较为简单,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。21世纪教育网版权所有
数形规律也是常考察题型之一,主要以数字数列、图形图表、算式等形式为主,考点和题型探索性和抽象性较强,一般学生解决起来稍显吃力,可着重进行强化训练。21教育网
【预测命题1】定义新运算。
例题:(2023·南京市小升初真题)对于两个数a与b,规定aθb=a×b+a+b。
(1)求6θ2;2θ6;
(2)求(17θ6)θ2;17θ(6θ2);
(3)这个运算θ有交换律和结合律吗?
解析:
【答案】(1)20;20;
(2)377;377
(3)θ有交换律和结合律。
【分析】第一、第二小题,根据给出的式子得出新的运算方法是:将运算符号的前后两个先相乘再相加,由此解答。
第三小题,根据交换律和结合律的意义,验证θ具有交换律和结合律即可。
【详解】(1)6θ2
=6×2+6+2
=12+6+2
=20
2θ6
=2×6+2+6
=12+2+6
=20
(2)(17θ6)θ2
=(17×6+17+6)θ2
=(102+17+6)θ2
=125θ2
=125×2+125+2
=250+125+2
=377
17θ(6θ2)
=17θ(6×2+6+2)
=17θ(12+6+2)
=17θ20
=17×20+17+20
=340+17+20
=377
(3)aθb
=a×b+a+b
=b×a+b+a
所以,aθb=bθa,即θ满足交换律。
(aθb)θc
=(a×b+a+b)θc
=(a×b+a+b)×c+a×b+a+b+c
=a×b×c+a×c+b×c+a×b+a+b+c
aθ(bθc)
=aθ(b×c+b+c)
=a×(b×c+b+c)+b×c+b+c
=a×b×c+a×c+b×c+a×b+a+b+c
所以,(aθb)θc= aθ(bθc),即θ具有结合律。
答:θ有交换律和结合律。
【点睛】关键是根据给出的式子,得出新的运算方法,再利用新的运算方法解决问题。
【真题练习】
1.(2023·长沙市小升初真题)对两个整数和定义新运算“”:,求。
2.(2023·成都市小升初真题)规定,,,,……如果,那么是几?
3.(2023·浏阳市小升初真题)规定“”为一种新运算,对于任意两个数和都有,如果,已知,求的值。
【预测命题2】数形规律。
例题:(2023·北京市小升初真题)餐馆内有一种长方形桌子,每张桌子周围放4把椅子,如果客人多,就按如图所示的方式拼桌。
现有14位客人要坐在一起,一共需要拼几张桌子?(可以选择画一画或算一算等方法)
解析:
【答案】6张
【分析】根据题意可知1张桌子4个人,2张桌子6个人,3张桌子8个人,可得到规律:每多1张桌子,会多2人,先用14-4求出第一张桌子坐满后多的人数,再除以2即可求出需要多加多少张桌子,再加上1即为一共需要拼几张桌子。据此解答即可。
【详解】14-4=10(人)
10÷2=5(张)
5+1=6(张)
答:一共需要拼6张桌子。
【真题练习】
1.(2023·武汉市小升初真题)下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形?
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
2.(2023·上海市小升初真题)数一数。
(1)图中各有多少个▲和△?
序号 ① ② ③ ④
▲ ( ) ( ) ( ) ( )
△ ( ) ( ) ( ) ( )
(2)照这样连续画下去,第7个图形中▲和△各有多少个?
3.(2023·天津市小升初真题)将小正方体按下图方式摆放在地上。
小正方体的个数 1 2 3 4 5 6
露在外面的面数
如果有50个正方体按上图摆放,露在外面的面有多少个?如果露在外面的面是129个,那是有几个正方体如上图摆放?
【预测命题3】数式规律。
例题:(2023·溧阳市小升初真题)三千多年前,埃及人发明了一种记录分数的方法,这些分数的分子为1,它们被称为“单位分数”,通过研究,小明发现一些分数可以很容易地拆分为两个不同的“单位分数”之和(或差)例如:
,;
,;
(1)请根据上述拆分方法将下列分数拆分为“单位分数”的和或差:
= ;= ;
(2)请运用上述拆分方法计算:。
解析:
【答案】(1);
(2)
【分析】(1)观察算式可知,若该分数的分子不是1,则把分数的分母拆成相邻的两个自然数的乘积形式,分子是这两个自然数和的形式,进而写成分母是两个数的乘积形式,分子分别是这两个数,再化简成分子为1的分数形式;若该分数的分子是1,则把分数的分母拆成相邻的两个自然数的乘积形式,分子是这两个自然数差的形式,而写成分母是两个数的乘积形式,分子分别是这两个数,再化简成分子为1的分数形式;
(2) 根据(1)中发现的规律,把算式中的每个分数进行拆分,去括号后,再运用加法结合律进行计算即可。
【详解】(1)=;=;
(2)
=
=
=
=
=
=
=
【点睛】本题主要考查算式的规律,数字的变化类,解答的关键是理解清楚所给的规律并灵活运用。
【真题练习】
1.(2023·无锡市小升初真题)探索与发现:奇思在乘法口诀表上发现一组有趣的算式,如:
6×6=36
5×7=35
4×8=32
3×9=27
(1)根据上面这组乘法算式的特点,在上面右边横线上再写一组这样的算式。
(2)观察上述这两组算式,你发现乘数怎样变化会引起积怎样变化?
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是( )。
A.(a+1)×(a-1)=a2+1
B.(a+1)×(a-1)=a2
C.(a+1)×(a-1)=a2-1
D.(a+2)×(a-2)=a2+2
(4)根据上面发现的规律,如果2022×2022=4088484,则2021×2023=( )。
2.(2023·青岛市小升初真题)先找规律再填空。(图中阴影表示每次截去后剩下的部分)
第四次截去后剩下,第( )次截去后剩下。
【预测命题4】数列规律。
例题:(2023·湘潭市小升初真题)已知一列数按294736294736294……排列,那么前40个数字之和是多少?
解析:
【答案】208
【分析】294736294736294……这一列数字是按照2、9、4、7、3、6这6个数字为一组进行循环出现的,求出40里面有多少个这样的一组,还余几;求出每组和,进而求出前40个数字的和。
【详解】2、9、4、7、3、6这6个数字为一组进行循环出现
2+9+4+7+3+6=31
40÷6=6(组)…4(个)
6组还余4个数字,余下的4个是2,9,4,7
2+9+4+7=22
31×6+22=208
答:前40个数字之和是208。
【点睛】解决这类问题往往是把重复出现的部分看成一组,先找出排列的周期性规律,再根据规律求解。
【真题练习】
1.(2023·株洲市小升初真题)丁丁也不甘示弱:你们知道著名的“斐波那契”数列吗?它是这样一组数:1,1,2,3,5,8,13,21,……从第三个数开始,以后每个数都是它前两个数的和,请问:前2016个数中共有多少个偶数?
2.(2023·徐州市小升初真题)(1)用一个长方形像图中那样任意圈出四个数字,你发现了什么规律?
(2)如果长方形中最上面一个数字用表示,最下面一个数字可以怎样表示?
(3)按这样的圈法,小丽圈出的四个数的和是200,你知道她圈的是哪四个数吗?算一算写出来。
3.(2023·重庆市小升初真题)有下面一串分数:;,,;,,,,;,,,,,,……
(1)是第几个分数?
(2)第400个分数是几分之几?
【命题猜想3】数式和数形综合——定义新运算与规律探索。
【命题说明】
定义新运算是指运用某种特殊符号来表示特定的意义,从而解答某些算式的一种运算,它是一种人为的、临时性的运算形式,它使用的是一些特殊的运算符号,如:*、△、⊙等,这是与四则运算中的“+、-、×、÷”不同的。
小升初中的新运算考察形式较为简单,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。21世纪教育网版权所有
数形规律也是常考察题型之一,主要以数字数列、图形图表、算式等形式为主,考点和题型探索性和抽象性较强,一般学生解决起来稍显吃力,可着重进行强化训练。21教育网
【预测命题1】定义新运算。
例题:(2023·南京市小升初真题)对于两个数a与b,规定aθb=a×b+a+b。
(1)求6θ2;2θ6;
(2)求(17θ6)θ2;17θ(6θ2);
(3)这个运算θ有交换律和结合律吗?
解析:
【答案】(1)20;20;
(2)377;377
(3)θ有交换律和结合律。
【分析】第一、第二小题,根据给出的式子得出新的运算方法是:将运算符号的前后两个先相乘再相加,由此解答。
第三小题,根据交换律和结合律的意义,验证θ具有交换律和结合律即可。
【详解】(1)6θ2
=6×2+6+2
=12+6+2
=20
2θ6
=2×6+2+6
=12+2+6
=20
(2)(17θ6)θ2
=(17×6+17+6)θ2
=(102+17+6)θ2
=125θ2
=125×2+125+2
=250+125+2
=377
17θ(6θ2)
=17θ(6×2+6+2)
=17θ(12+6+2)
=17θ20
=17×20+17+20
=340+17+20
=377
(3)aθb
=a×b+a+b
=b×a+b+a
所以,aθb=bθa,即θ满足交换律。
(aθb)θc
=(a×b+a+b)θc
=(a×b+a+b)×c+a×b+a+b+c
=a×b×c+a×c+b×c+a×b+a+b+c
aθ(bθc)
=aθ(b×c+b+c)
=a×(b×c+b+c)+b×c+b+c
=a×b×c+a×c+b×c+a×b+a+b+c
所以,(aθb)θc= aθ(bθc),即θ具有结合律。
答:θ有交换律和结合律。
【点睛】关键是根据给出的式子,得出新的运算方法,再利用新的运算方法解决问题。
【真题练习】
1.(2023·长沙市小升初真题)对两个整数和定义新运算“”:,求。
【答案】
【分析】由可知:定义新运算“”的意义是:分子是前面数的2倍减去后面的数,分母是前面数加后面数的和乘前面数减后面数的差,代入数据计算即可。
【详解】
=+
=+
=
【点睛】解答此类问题,关键是要正确理解新定义的算式含义,严格按照定义新运算的计算程序将数值代入,转化为常规的四则运算算式进行计算。
2.(2023·成都市小升初真题)规定,,,,……如果,那么是几?
【答案】
【分析】将化为:再根据等式的性质进行解答即可。
【详解】由,可得:
进而得出
根据等式的性质2得:A+1=÷,将=5×6×7,=6×7×8代入可得:
A+1=÷
所以A=-1=
答:是。
【点睛】本题是一道稍复杂的等量代换,合理运用等式的性质是解题的关键。
3.(2023·浏阳市小升初真题)规定“”为一种新运算,对于任意两个数和都有,如果,已知,求的值。
【答案】x=
【分析】根据题中的新定义计算即可。
【详解】根据题中的新定义可得:+=5
解方程可得x=
答:的值是。
【点睛】本题是一道定义新运算问题,解题的关键是正确理解定义的运算符号的意义。
【预测命题2】数形规律。
例题:(2023·北京市小升初真题)餐馆内有一种长方形桌子,每张桌子周围放4把椅子,如果客人多,就按如图所示的方式拼桌。
现有14位客人要坐在一起,一共需要拼几张桌子?(可以选择画一画或算一算等方法)
解析:
【答案】6张
【分析】根据题意可知1张桌子4个人,2张桌子6个人,3张桌子8个人,可得到规律:每多1张桌子,会多2人,先用14-4求出第一张桌子坐满后多的人数,再除以2即可求出需要多加多少张桌子,再加上1即为一共需要拼几张桌子。据此解答即可。
【详解】14-4=10(人)
10÷2=5(张)
5+1=6(张)
答:一共需要拼6张桌子。
【真题练习】
1.(2023·武汉市小升初真题)下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形?
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
【答案】绿色6个;蓝色18个;绿色10个;蓝色26个;见详解
【分析】第1个图形,有1个绿色小正方形,8个蓝色小正方形,8=2×1+6;
第2个图形,有2个绿色小正方形,10个蓝色小正方形,10=2×2+6;
第3个图形,有3个绿色小正方形,12个蓝色小正方形,12=2×3+6;
第4个图形,有4个绿色小正方形,14个蓝色小正方形,14=2×4+6;
……
规律:第n个图形,有n个绿色小正方形,(2n+6)个蓝色小正方形;据此解答。
【详解】规律:第n个图形,有n个绿色小正方形,(2n+6)个蓝色小正方形。
当n=6时,有6个绿色小正方形;
蓝色小正方形有:
2n+6
=2×6+6
=12+6
=18(个)
当n=10时,有10个绿色小正方形;
蓝色小正方形有:
2n+6
=2×10+6
=20+6
=26(个)
答:照这样接着画下去,第6个图形有6个绿色小正方形和18个蓝色小正方形。第10个图形有10个绿色小正方形和26个蓝色小正方形。
道理:从图中发现规律:第n个图形有n个绿色小正方形,(2n+6)个蓝色小正方形。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
2.(2023·上海市小升初真题)数一数。
(1)图中各有多少个▲和△?
序号 ① ② ③ ④
▲ ( ) ( ) ( ) ( )
△ ( ) ( ) ( ) ( )
(2)照这样连续画下去,第7个图形中▲和△各有多少个?
【答案】(1)1;3;6;10
3;6;10;15
(2)▲有28个;△有36个
【分析】第1个图有1个▲,第2个图有1+2=3(个)▲,第3个图有1+2+3=6(个)▲,第4个图有1+2+3+4=10(个)▲,……由此发现规律:第n图有(1+2+3+4+…+n)个▲。
第1个图有1+2=3(个)△,第2个图有1+2+3=6(个)△,第3个图有1+2+3+4=10(个)△,第4个图有1+2+3+4+5=15(个)△……由此发现规律:第n图有[1+2+3+4+…+(n+1)]个△。
【详解】(1)▲的个数:
第1个图:1个
第2个图:1+2=3(个)
第3个图:1+2+3=6(个)
第4个图:1+2+3+4=10(个)
△的个数:
第1个图:1+2=3(个)
第2个图:1+2+3=6(个)
第3个图:1+2+3+4=10(个)
第4个图:1+2+3+4+5=15(个)
如下表:
序号 ① ② ③ ④
▲ 1 3 6 10
△ 3 6 10 15
(2)1+2+3+4+5+6+7=28(个)
1+2+3+4+5+6+7+8=36(个)
答:第7个图形中▲有28个,△各有36个。
【点睛】在运用数形结合的方法探究数学规律时,一定要把图形和数一一对应。
3.(2023·天津市小升初真题)将小正方体按下图方式摆放在地上。
小正方体的个数 1 2 3 4 5 6
露在外面的面数
如果有50个正方体按上图摆放,露在外面的面有多少个?如果露在外面的面是129个,那是有几个正方体如上图摆放?
【答案】表格见详解;201个;32个
【分析】由题意可知,有1个小正方体露在外面的面数有5面,2个小正方体露在外面的面数有9个,3个小正方体露在外面的面数有13个,则有n个正方体,则露在外面的面有(4n+1)个,据此解答即可。
【详解】当n=4时
4n+1=4×4+1
=16+1
=17(个)
当n=5时
4n+1=4×5+1
=20+1
=21(个)
当n=6时
4n+1=4×6+1
=24+1
=25(个)
当n=50时
4n+1=4×50+1
=200+1
=201(个)
解:设如果露在外面的面是129个,那是有x个正方体如上图摆放。
4n+1=129
4n+1-1=129-1
4n=128
4n÷4=128÷4
n=32
则如果有50个正方体按上图摆放,露在外面的面有201个,如果露在外面的面是129个,那是有32个正方体如上图摆放。
如图所示:
小正方体的个数 1 2 3 4 5 6
露在外面的面数 5 9 13 17 21 25
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
【预测命题3】数式规律。
例题:(2023·溧阳市小升初真题)三千多年前,埃及人发明了一种记录分数的方法,这些分数的分子为1,它们被称为“单位分数”,通过研究,小明发现一些分数可以很容易地拆分为两个不同的“单位分数”之和(或差)例如:
,;
,;
(1)请根据上述拆分方法将下列分数拆分为“单位分数”的和或差:
= ;= ;
(2)请运用上述拆分方法计算:。
解析:
【答案】(1);
(2)
【分析】(1)观察算式可知,若该分数的分子不是1,则把分数的分母拆成相邻的两个自然数的乘积形式,分子是这两个自然数和的形式,进而写成分母是两个数的乘积形式,分子分别是这两个数,再化简成分子为1的分数形式;若该分数的分子是1,则把分数的分母拆成相邻的两个自然数的乘积形式,分子是这两个自然数差的形式,而写成分母是两个数的乘积形式,分子分别是这两个数,再化简成分子为1的分数形式;
(2) 根据(1)中发现的规律,把算式中的每个分数进行拆分,去括号后,再运用加法结合律进行计算即可。
【详解】(1)=;=;
(2)
=
=
=
=
=
=
=
【点睛】本题主要考查算式的规律,数字的变化类,解答的关键是理解清楚所给的规律并灵活运用。
【真题练习】
1.(2023·无锡市小升初真题)探索与发现:奇思在乘法口诀表上发现一组有趣的算式,如:
6×6=36
5×7=35
4×8=32
3×9=27
(1)根据上面这组乘法算式的特点,在上面右边横线上再写一组这样的算式。
(2)观察上述这两组算式,你发现乘数怎样变化会引起积怎样变化?
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是( )。
A.(a+1)×(a-1)=a2+1
B.(a+1)×(a-1)=a2
C.(a+1)×(a-1)=a2-1
D.(a+2)×(a-2)=a2+2
(4)根据上面发现的规律,如果2022×2022=4088484,则2021×2023=( )。
【答案】(1)7×7=49
6×8=48
5×9=45
4×10=40
(2)两个相同的因数相乘,如果一个因数加n,另一个因数减n,积就等于因数的平方减n2。
(3)C
(4)4088483
【分析】根据算式的规律,可以发现:
6×6和5×7之间的规律可以用字母表示出来:(a+1)×(a-1)=a2-1;
6×6和4×8之间的规律可以用字母表示出来:(a+2)×(a-2)=a2-22;
6×6和3×9之间的规律可以用字母表示出来:(a+3)×(a-3)=a2-32;
据此结合题意解答即可。
【详解】(1)根据上面这组乘法算式的特点,在右边横线上再写一组这样的算式:
7×7=49
6×8=48
5×9=45
4×10=40(答案不唯一)
(2)观察上述这两组算式,发现:两个相同的因数相乘,如果一个因数加n,另一个因数减n,积就等于因数的平方减n2。
(3)奇思发现6×6和5×7之间的规律可以用字母表示出来,下面正确的是(a+1)×(a-1)=a2-1
故答案为:C
(4)根据上面发现的规律,如果2022×2022=4088484,则:
2021×2023
=2022×2022-1
=4088484-1
=4088483
【点睛】本题考查了式的规律知识,结合题意分析解答即可。
2.(2023·青岛市小升初真题)先找规律再填空。(图中阴影表示每次截去后剩下的部分)
第四次截去后剩下,第( )次截去后剩下。
【答案】规律:第几次截去后剩下的就用1连续乘几个;16;7
【分析】观察图形可知,每次剩下,第一次1×;第二次1××;第三次1×××,第几次就用1连续乘几个;据此解答。
【详解】规律:第几次截去后剩下的就用1连续乘几个。
1××××
=×××
=××
=×
=
第五次截去后还剩:×=
第六次截去后还剩:×=
第七次截去后还剩:×=
第四次截去后剩下,第7次截去后剩下。
【点睛】在数学算式中探索规律,需要仔细观察算式特点,找出规律,根据规律填出这一类算式的结果。
【预测命题4】数列规律。
例题:(2023·湘潭市小升初真题)已知一列数按294736294736294……排列,那么前40个数字之和是多少?
解析:
【答案】208
【分析】294736294736294……这一列数字是按照2、9、4、7、3、6这6个数字为一组进行循环出现的,求出40里面有多少个这样的一组,还余几;求出每组和,进而求出前40个数字的和。
【详解】2、9、4、7、3、6这6个数字为一组进行循环出现
2+9+4+7+3+6=31
40÷6=6(组)…4(个)
6组还余4个数字,余下的4个是2,9,4,7
2+9+4+7=22
31×6+22=208
答:前40个数字之和是208。
【点睛】解决这类问题往往是把重复出现的部分看成一组,先找出排列的周期性规律,再根据规律求解。
【真题练习】
1.(2023·株洲市小升初真题)丁丁也不甘示弱:你们知道著名的“斐波那契”数列吗?它是这样一组数:1,1,2,3,5,8,13,21,……从第三个数开始,以后每个数都是它前两个数的和,请问:前2016个数中共有多少个偶数?
【答案】672个
【分析】由奇数+奇数=偶数,偶数十奇数=奇数,从而可以发现斐波那契数列中数列是以“奇数、奇数、偶数、奇数、奇数、偶数……”3个一周期排列的,所以2016÷3=672(个)周期,每个周期里有1个偶数,672×1=672(个),即有672个偶数。
【详解】2016÷3=672(个)
672×1=672(个)
答:前2016个数中共有672个偶数。
【点睛】找到题干中的数列规律是解题的关键。
2.(2023·徐州市小升初真题)(1)用一个长方形像图中那样任意圈出四个数字,你发现了什么规律?
(2)如果长方形中最上面一个数字用表示,最下面一个数字可以怎样表示?
(3)按这样的圈法,小丽圈出的四个数的和是200,你知道她圈的是哪四个数吗?算一算写出来。
【答案】(1)每相邻两个之间相差10;
(2);
(3)35、45、55、65。
【分析】(1)观察上下相邻的数之间的大小关系,得出规律;
(2)长方形中一共有4个数,最上面和最下面之间相差30,据此列式;
(3)设小丽圈出的第一个数字为,下面的数依次是a+10、a+20、a+30,根据四个数相加等于200,列出方程,求出第一个数,再分别求出下面的数即可。
【详解】(1)我发现圈出的4个数,每相邻两个之间相差10。
(2)最下面一个数字可以用表示。
(3)解:设小丽圈出的第一个数字为。
4+60=200
4=140
,,。
答:她圈的是35、45、55、65。
【点睛】本题考查了数字的排列规律和列方程解决问题,关键是发现数表中的规律。
3.(2023·重庆市小升初真题)有下面一串分数:;,,;,,,,;,,,,,,……
(1)是第几个分数?
(2)第400个分数是几分之几?
【答案】(1)第88个和第94个 (2)
【详解】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
