第一章 第6 节 微积分基本定理
文档属性
| 名称 | 第一章 第6 节 微积分基本定理 |  | |
| 格式 | rar | ||
| 文件大小 | 112.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-05 11:32:00 | ||
图片预览







文档简介
课件25张PPT。1.6 微积分基本定理问题提出 1.定积分 的含义是什么?其
中a与b,区间[a,b],函数f(x),变量x,f(x)dx分别叫什么名称?a:积分下限; b:积分上限;
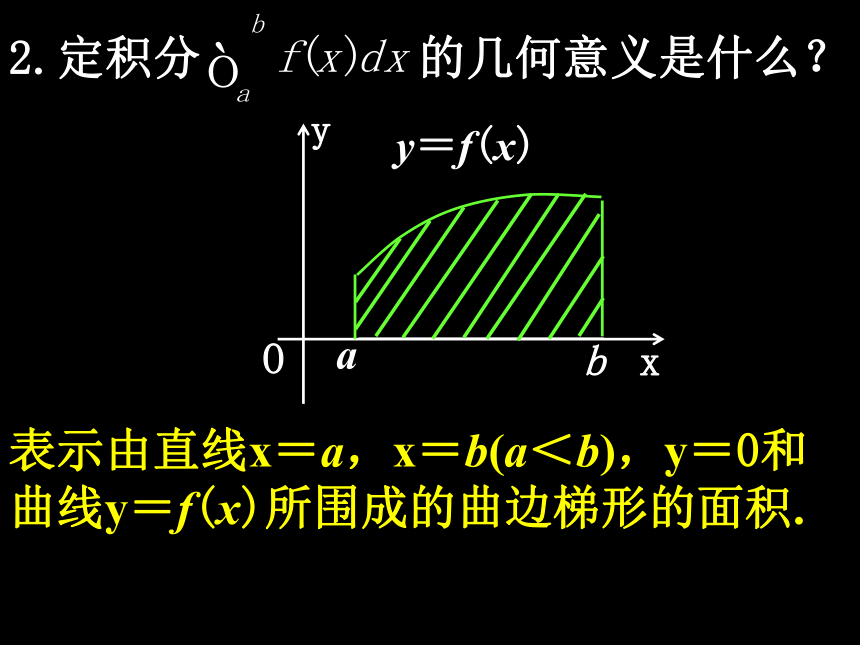
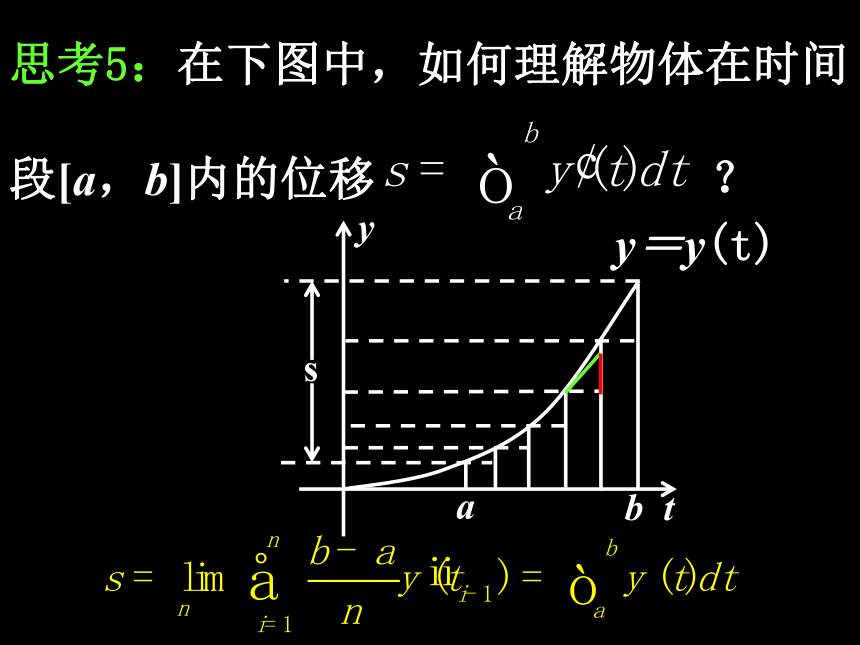
[a,b]:积分区间; f(x):被积函数; x:积分变量; f(x)dx:被积式.2.定积分 的几何意义是什么? 表示由直线x=a,x=b(a<b),y=0和曲线y=f(x)所围成的曲边梯形的面积. 3.定积分有哪几条基本运算性质?(1)(2)(3) 4.直接用定积分的定义计算的值是很烦琐的,有些定积分几乎不能直接用定义计算,因此寻求一个简便、有效的计算原理求定积分的值,就成为一个迫切需要解决的问题. 5.我们已经掌握了导数的概念和计算方法,如果能建立导数与定积分的内在联系,利用导数来求定积分,那是非常理想和美妙的.微积分基本定理探究(一):物体位移的几种算法 思考1:一个作变速直线运动的物体的位移y与时间t的函数关系为y=y(t),那么它在时间段[a,b]内的位移s等于什么?s=y(b)-y(a). 思考2:设物体的速度v与时间t的函数关系为v=v(t),那么它在时间段[a,b]内的位移s用定积分怎样表示? 思考3:物体在时刻t的速度v(t)与位移y(t)的关系是什么?v(t)=y'(t).思考4:综上分析,物体在时间段[a,b]内的位移s有哪些表示式? 思考5:在下图中,如何理解物体在时间
段[a,b]内的位移 ? 探究(二):微积分基本定理 思考1:我们曾求得以速度v(t)=-t2+2作变速直线运动的汽车,在0≤t≤1时段内行驶的路程为定积分 ,
若利用上述原理求定积分 的值,如何计算? 思考2:我们曾利用定积分的定义和性质
求得 , ,
若利用上述原理求这两个定积分,如何计算? 思考3:一般地,如果f(x)是区间[a,b]上的连续函数,并且 ,
那么 等于什么? 思考4:定积分
叫做微积分基本定理,又叫做牛顿-莱布尼兹公式,为了方便,我们常把F(b)-F(a)记成 .那么用微积分基本定
理计算定积分 的关键是什么? 找到满足 的函数F(x). 思考5:对给定的函数f(x),满足
的函数F(x)是不惟一的,不同的F(x)有什么差别?对定积分
的值是否有影响?若 ,则 . 没有影响!理论迁移 例 计算下列定积分:
(1) ;(2) . 1.微积分基本定理是微积分中最重要、最辉煌的成果,它揭示了导数和定积分之间的内在联系,同时它也提供了计算定积分的一种有效办法.小结作业 2.寻找满足 的函数F(x),一般运用基本初等函数的求导公式和导数的四则运算法则,从反方向上求出F(x).作业:
P55练习:(1)~(4).
P55习题1.6A组:1.微积分基本定理习题课 第一课时 定积分的计算 例1 计算下列定积分,利用曲边梯形的面积,你能从计算结果中发现什么结论吗?(1) ;(2) ;
(3) . 2-20【结论】
(1)当定积分对应的曲边梯形位于x轴上方时,定积分的值为正数,且等于曲边梯形的面积;(2)当定积分对应的曲边梯形位于x轴下方时,定积分的值为负数,且等于曲边梯形的面积的相反数;(3)当定积分对应的曲边梯形位于x轴上方部分的面积与位于x轴下方部分的面积相等时,定积分的值为零.(4)若f(x)为奇函数,则
;(5)若f(x)为偶函数,则
,
其中a>0为常数. 例2 计算下列定积分:(1) ; (2) ; (3) ; (4) . 0 例3 计算下列定积分: (1) ; (2) . 例4 汽车以36km/h的速度行驶,到某处需减速停车.设汽车以加速度a=2m/s2刹车,试问:从开始刹车到停车,汽车走过的路程是多少m?
中a与b,区间[a,b],函数f(x),变量x,f(x)dx分别叫什么名称?a:积分下限; b:积分上限;
[a,b]:积分区间; f(x):被积函数; x:积分变量; f(x)dx:被积式.2.定积分 的几何意义是什么? 表示由直线x=a,x=b(a<b),y=0和曲线y=f(x)所围成的曲边梯形的面积. 3.定积分有哪几条基本运算性质?(1)(2)(3) 4.直接用定积分的定义计算的值是很烦琐的,有些定积分几乎不能直接用定义计算,因此寻求一个简便、有效的计算原理求定积分的值,就成为一个迫切需要解决的问题. 5.我们已经掌握了导数的概念和计算方法,如果能建立导数与定积分的内在联系,利用导数来求定积分,那是非常理想和美妙的.微积分基本定理探究(一):物体位移的几种算法 思考1:一个作变速直线运动的物体的位移y与时间t的函数关系为y=y(t),那么它在时间段[a,b]内的位移s等于什么?s=y(b)-y(a). 思考2:设物体的速度v与时间t的函数关系为v=v(t),那么它在时间段[a,b]内的位移s用定积分怎样表示? 思考3:物体在时刻t的速度v(t)与位移y(t)的关系是什么?v(t)=y'(t).思考4:综上分析,物体在时间段[a,b]内的位移s有哪些表示式? 思考5:在下图中,如何理解物体在时间
段[a,b]内的位移 ? 探究(二):微积分基本定理 思考1:我们曾求得以速度v(t)=-t2+2作变速直线运动的汽车,在0≤t≤1时段内行驶的路程为定积分 ,
若利用上述原理求定积分 的值,如何计算? 思考2:我们曾利用定积分的定义和性质
求得 , ,
若利用上述原理求这两个定积分,如何计算? 思考3:一般地,如果f(x)是区间[a,b]上的连续函数,并且 ,
那么 等于什么? 思考4:定积分
叫做微积分基本定理,又叫做牛顿-莱布尼兹公式,为了方便,我们常把F(b)-F(a)记成 .那么用微积分基本定
理计算定积分 的关键是什么? 找到满足 的函数F(x). 思考5:对给定的函数f(x),满足
的函数F(x)是不惟一的,不同的F(x)有什么差别?对定积分
的值是否有影响?若 ,则 . 没有影响!理论迁移 例 计算下列定积分:
(1) ;(2) . 1.微积分基本定理是微积分中最重要、最辉煌的成果,它揭示了导数和定积分之间的内在联系,同时它也提供了计算定积分的一种有效办法.小结作业 2.寻找满足 的函数F(x),一般运用基本初等函数的求导公式和导数的四则运算法则,从反方向上求出F(x).作业:
P55练习:(1)~(4).
P55习题1.6A组:1.微积分基本定理习题课 第一课时 定积分的计算 例1 计算下列定积分,利用曲边梯形的面积,你能从计算结果中发现什么结论吗?(1) ;(2) ;
(3) . 2-20【结论】
(1)当定积分对应的曲边梯形位于x轴上方时,定积分的值为正数,且等于曲边梯形的面积;(2)当定积分对应的曲边梯形位于x轴下方时,定积分的值为负数,且等于曲边梯形的面积的相反数;(3)当定积分对应的曲边梯形位于x轴上方部分的面积与位于x轴下方部分的面积相等时,定积分的值为零.(4)若f(x)为奇函数,则
;(5)若f(x)为偶函数,则
,
其中a>0为常数. 例2 计算下列定积分:(1) ; (2) ; (3) ; (4) . 0 例3 计算下列定积分: (1) ; (2) . 例4 汽车以36km/h的速度行驶,到某处需减速停车.设汽车以加速度a=2m/s2刹车,试问:从开始刹车到停车,汽车走过的路程是多少m?
