8.6.3 平面与平面垂直(二) 学案
文档属性
| 名称 | 8.6.3 平面与平面垂直(二) 学案 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
8.6.3 平面与平面垂直(二)
平面与平面垂直的性质
班级 姓名
学习目标
1.掌握平面与平面垂直的性质定理,学会用定理证明垂直关系.
2.熟悉线线垂直、线面垂直、面面垂直间判定和性质的转化.
学习过程
自学指导 自学检测及课堂展示
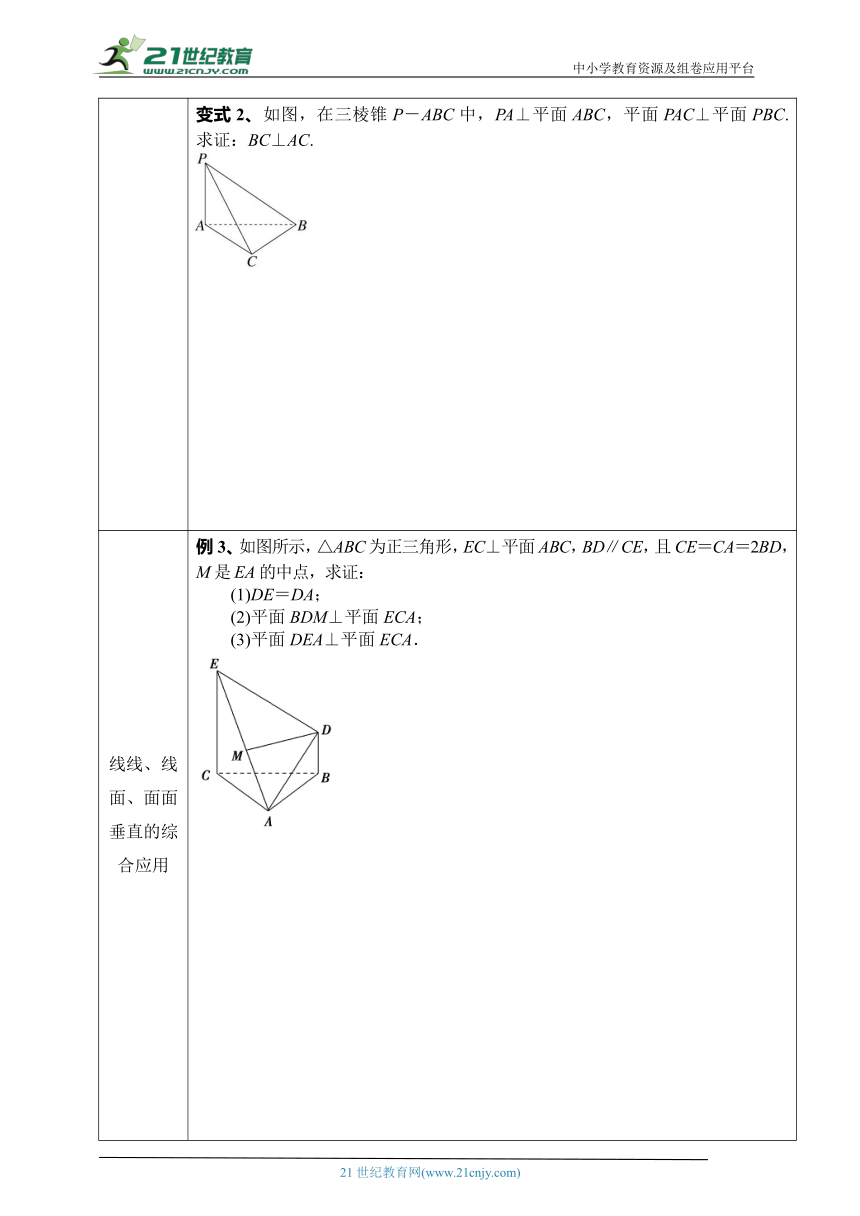
阅读教材,完成右边的内容 平面与平面垂直的性质定理文字语言两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直符号语言图形语言作用①面面垂直 线面垂直 ②作面的垂线【即时训练】(1)(多选题)已知两个平面垂直,下列命题中不正确的是( )A.—个平面内的已知直线必垂直于另—个平面内的任意—条直线B.一个平面内的已知直线必垂直于另一个平面的无数条直线C.一个平面内的任一条直线必垂直于另一个平面D.过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面(2)对于直线m,n和平面α,β,能得出α⊥β的一个条件是( )A.m⊥n,m∥α,n∥β B.m⊥n,α∩β=m,n αC.m∥n,n⊥β,m α D.m∥n,m⊥α,n⊥β
平面与平面垂直的性质定理 例2、如图,P是边长为a的菱形ABCD所在平面外的一点,∠DAB=60°.侧面PAD为正三角形,其所在平面垂直于底面ABCD.(1)若G为AD边的中点,求证:BG⊥平面PAD;(2)求证:AD⊥PB.变式2、如图,在三棱锥P-ABC中,PA⊥平面ABC,平面PAC⊥平面PBC.求证:BC⊥AC.
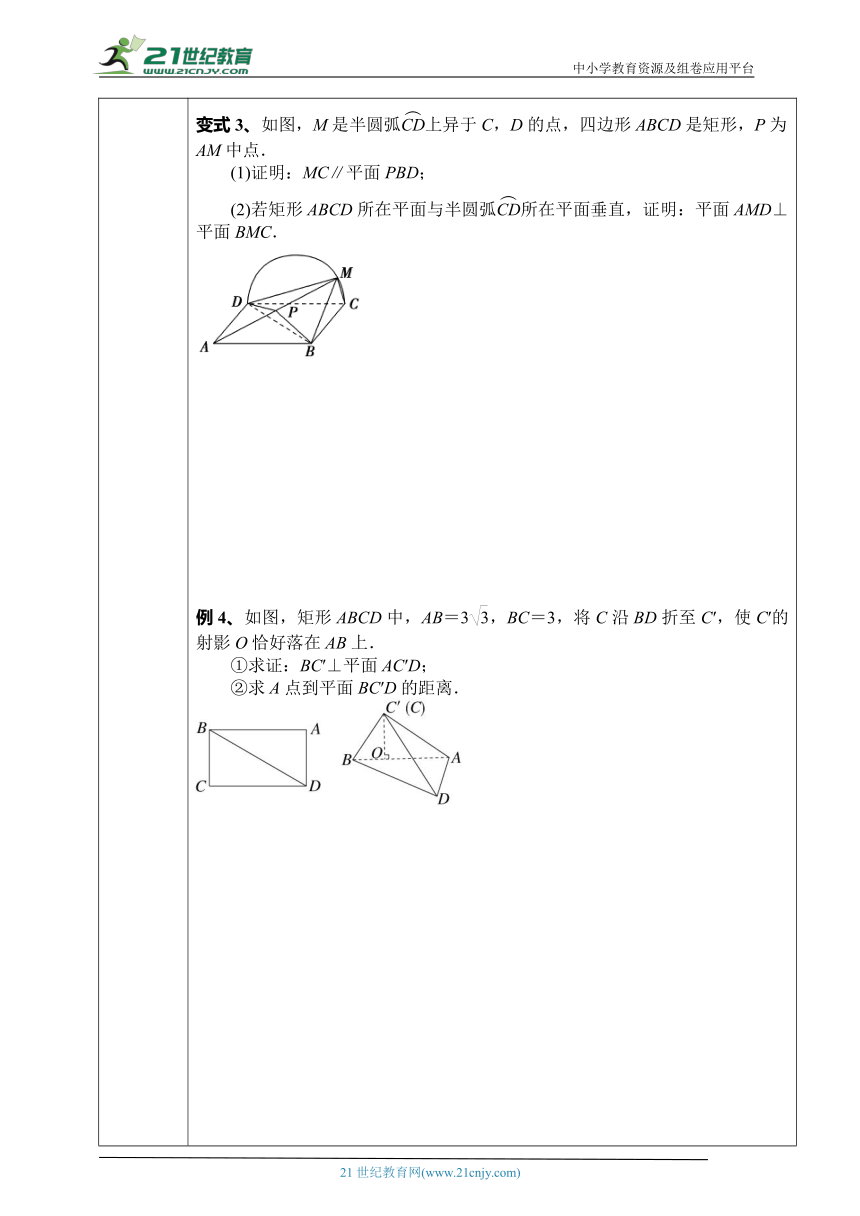
变式3、如图,M是半圆弧上异于C,D的点,四边形ABCD是矩形,P为AM中点.(1)证明:MC∥平面PBD;(2)若矩形ABCD所在平面与半圆弧所在平面垂直,证明:平面AMD⊥平面BMC.例4、如图,矩形ABCD中,AB=3,BC=3,将C沿BD折至C′,使C′的射影O恰好落在AB上.①求证:BC′⊥平面AC′D;②求A点到平面BC′D的距离.
课后作业
一、基础训练题
1.(多选题)下列命题中正确的是( )
A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ
D.如果平面α⊥平面β,那么平面α内的所有直线都垂直于平面β
2.设平面α⊥平面β,在平面α内的一条直线a垂直于平面β内的一条直线b,则( )
A.直线a必垂直于平面β B.直线b必垂直于平面α
C.直线a不一定垂直于平面β D.过a的平面与过b的平面垂直
3.若平面α⊥平面β,平面β⊥平面γ,则( )
A.α∥γ B.α⊥γ
C.α与γ相交但不垂直 D.以上都有可能
4.《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.
设AA1是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点,
以AA1为底面矩形的一边,则这样的阳马的个数是( )
A.8 B.12 C.16 D.18
5.已知平面α⊥平面β,α∩β=l,点A∈α,A l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是( )
A.AB∥m B.AC⊥m C.AB∥β D.AC⊥β
6.如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )
A.平面ADC⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ABD⊥平面ABC
7.(多选题)如图,点P为四边形ABCD外一点,平面PAD⊥平面ABCD,PA=PD,E为AD的中点,则下列结论不一定成立的是( )
A.PE⊥AC B.PE⊥BC
C.平面PBE⊥平面ABCD
D.平面PBE⊥平面PAD
8.已知α,β是两个不同的平面,l是平面α与β之外的直线,给出下列三个论断:
①l⊥α,②l∥β,③α⊥β.以其中的两个论断作为条件,余下的一个论断作为结论,
写出你认为正确的一个命题:________.(用序号表示)
9.如下左图,△ABC是等腰直角三角形,∠BAC=90°,AB=AC=1,将△ABC沿斜线BC上的高AD折叠,使平面ABD⊥平面ACD,则BC=________.
10.如上右图,空间四边形ABCD中,平面ABD⊥平面BCD,∠BAD=90°,且AB=AD,则AD与平面BCD所成的角是________.
11.已知m,n是两条不相同的直线,α,β是两个不重合的平面,现有以下说法:
①若α∥β,n α,m β,则m∥n;
②若m⊥α,m⊥β,n⊥α,则n⊥β;
③若m⊥n,m⊥α,n⊥β,则α⊥β;
④若m∥α,n∥β,α⊥β,则m⊥n;
⑤若α⊥β,m α,n β,则m⊥n.
其中正确说法的序号有________.
12.如图,已知△ABC为等边三角形,△ABD为等腰直角三角形,AB⊥BD,平面ABC⊥平面ABD,点E与点D在平面ABC的同侧,且CE∥BD,BD=2CE,点F为AD中点,连接EF.
求证:平面AED⊥平面ABD.
13.如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
求证:平面AEC⊥平面AFC.
14.如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E,F分别是棱PC和PD的中点.
(1)求证:EF∥平面PAB;
(2)若AP=AD,且平面PAD⊥平面ABCD,证明:AF⊥平面PCD.
15.如图1,在直角梯形ABCD中,AD∥BC,∠BAD=,AB=BC=AD=a,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1-BCDE.
(1)证明:CD⊥平面A1OC;
(2)当平面A1BE⊥平面BCDE时,四棱锥A1-BCDE的体积为36,求a的值.
二、综合训练题
16.如图,正方体ABCD-A1B1C1D1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,有下面三个结论:
①点H是△A1BD的中心;
②AH垂直于平面CB1D1;
③直线AC1与直线B1C所成的角是90°.
其中正确结论的序号是________.
17.如图,线段AB的两端在直二面角α-l-β的两个面内,并与这两个面都成30°角,则异面直线AB与l所成的角是( )
A.30° B.45°
C.60° D.75°
三、能力提升题
18.如图所示,四棱锥P-ABCD中,△PAB与△PBC是正三角形,
AC⊥BD,则下列结论不一定成立的是( )
A.PB⊥AC
B.PD⊥平面ABCD
C.AC⊥PD
D.平面PBD⊥平面ABCD
19.(多选题)如图,在四面体P ABC中,AB=AC,PB=PC,D,E,F分别是棱AB,BC,CA的中点,则下列结论中一定成立的是( )
A.BC∥平面PDF
B.DF⊥平面PAE
C.平面PDF⊥平面PAE
D.平面PDF⊥平面ABC
20.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AB∥CD,
AB⊥AD,且CD=2AB.
(1)若AB=AD,直线PB与CD所成的角为45°,求二面角P-CD-B的大小;
(2)若E为线段PC上一点,试确定点E的位置,使得平面EBD⊥平面ABCD,并说明理由.
8.6.3 平面与平面垂直(二)
1、【答案】ABC
【解析】平面α⊥平面β,α∩β=l,直线a在平面α内,且a∥l,所以a∥β,所以A正确,D错误.
若平面α内存在垂直于平面β的直线,根据面面垂直的判定定理,有平面α⊥平面β,与前提矛盾,
所以B正确.
设平面α∩平面γ=m,平面β∩平面γ=n,
在平面γ内任取一点A,过该点作c⊥m,d⊥n,且c,d γ.
因为平面α⊥平面γ,平面α∩平面γ=m,c 平面γ,所以c⊥平面α.
又l 平面α,所以l⊥c.同理l⊥d.
因为c∩d=A,所以l⊥平面γ.所以C正确.
2、【答案】C
【解析】当b=α∩β时,必有a⊥β;当b不是α与β的交线时,直线a不一定垂直于平面β.
3、【答案】D
【解析】两个平面都垂直于同一个平面,则这两个平面可能平行,也可能相交,
故A,B,C都有可能.
4、【答案】C
【解析】如图,根据正六边形的性质可知,以四边形A1ABB1,A1AFF1,A1ACC1和A1AEE1为底面矩形,各有4个阳马,故共有4×4=16(个)阳马.故选C.
5、【答案】D
【解析】如图,AB∥l∥m,AC⊥l,m∥α AC⊥m,AB∥l AB∥β. 故选D.
6、【答案】A
解析 易知CD⊥BD,又平面ABD⊥平面BCD,
且平面ABD∩平面BCD=BD,CD 平面BCD,
∴CD⊥平面ABD,又BA 平面ABD,∴CD⊥BA.
又BA⊥AD,且AD∩CD=D,AD,CD 平面ADC,
∴BA⊥平面ADC,又BA 平面ABC,
∴平面ADC⊥平面ABC.
7、【答案】ABC
【解析】因为PA=PD,E为AD的中点,所以PE⊥AD.又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,所以PE⊥平面ABCD,所以PE⊥AC,PE⊥BC,
所以A,B结论一定成立.又PE 平面PBE,所以平面PBE⊥平面ABCD,
所以C结论一定成立.若平面PBE⊥平面PAD,则AD⊥平面PBE,必有AD⊥BE,
此关系不一定成立,故选ABC.
8、【答案】①② ③(答案不唯一)
【解析】由l∥β可在平面β内作l′∥l,又l⊥α,∴l′⊥α,∵l′ β,∴α⊥β,故①② ③.
9、【答案】1
【解析】因为AD⊥BC,所以AD⊥BD,AD⊥CD,
所以∠BDC是二面角B AD C的平面角,
因为平面ABD⊥平面ACD,所以∠BDC=90°.
在△BCD中∠BDC=90°,又AB=AC=1,
所以BD=CD=,所以BC==1.
10、【答案】45°
【解析】如图,过A作AO⊥BD于O 点,∵平面ABD⊥平面BCD,∴AO⊥平面BCD,
则∠ADO即为AD与平面BCD所成的角.∵∠BAD=90°,AB =AD.∴∠ADO=45°.
11、【答案】②③
【解析】对于①,分别位于两个平行平面内的两条直线未必平行,可能是异面直线,因此①不正确;
对于②,由定理“垂直于同一直线的两个平面平行”得α,β平行,由性质“若一条直线垂直于两个平行平面中的一个,则它也垂直于另一个平面”得n⊥β,因此②正确;
对于③,由性质“由空间一点向一个二面角的两个半平面分别引垂线,则这两条垂线所成的角与该二面角相等或互补”得③正确;
对于④,分别平行两个垂直平面的两条直线未必垂直,因此④不正确;对于⑤,m与n还有可能平行或异面,因此⑤不正确.综上所述,说法正确的有②③.
12、【证明】取AB中点O,连接OC,OF.
∵O,F分别为AB,AD中点,则OF∥BD且BD=2OF.
又∵CE∥BD且BD=2CE,
∴CE∥OF且CE=OF,
∴四边形OCEF为平行四边形,∴EF∥OC.
∵△ABC为等边三角形,∴OC⊥AB.
又∵平面ABC⊥平面ABD,且平面ABC∩平面ABD=AB,
∴OC⊥平面ABD.
∵EF∥OC,∴EF⊥平面ABD,又∵EF 平面AED,
∴平面AED⊥平面ABD.
13、【证明】如图,连接BD,设BD交AC于点G,连接EG,FG,EF.
在菱形ABCD中,不妨设GB=1,
由∠ABC=120°,可得AG=GC=.
由BE⊥平面ABCD,AB=BC,可知AE=EC.
又AE⊥EC,所以EG=,且EG⊥AC.
在Rt△EBG中,BE==,故DF=.
在Rt△FDG中,FG==.
在直角梯形BDFE中,由BD=2,BE=,DF=,可得EF=.
因为EG2+FG2=EF2,所以EG⊥FG.
又AC∩FG=G,所以EG⊥平面AFC.
又EG 平面AEC,所以平面AEC⊥平面AFC.
14、【证明】(1)∵E,F分别是棱PC和PD的中点,
∴EF∥CD,
又在矩形ABCD中,AB∥CD,
∴EF∥AB,
∵AB 平面PAB,EF 平面PAB,
∴EF∥平面PAB.
(2)在矩形ABCD中,AD⊥CD,
又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,CD 平面ABCD,
∴CD⊥平面PAD,
又AF 平面PAD,∴CD⊥AF.
∵PA=AD,F是PD的中点,∴AF⊥PD,
∵PD 平面PCD,CD 平面PCD,PD∩CD=D,∴AF⊥平面PCD.
15、【解】①证明:在题图1中,由已知条件易得BE⊥AC,
即在题图2中,BE⊥A1O,BE⊥OC,
又A1O∩OC=O,∴BE⊥平面A1OC.
易知四边形BCDE是平行四边形,
∴BE∥CD,∴CD⊥平面A1OC.
②已知平面A1BE⊥平面BCDE,且平面A1BE∩平面BCDE=BE.
又由①知,A1O⊥BE,
∴A1O⊥平面BCDE,即A1O是四棱锥A1-BCDE的高.
易知A1O=a,S四边形BCDE=a·a=a2,
从而四棱锥A1-BCDE的体积V=×S四边形BCDE×A1O=×a2×a=a3=36,解得a=6.
16、【答案】①②③
【解析】①正确,连接A1H,BH,DH.
因为AB=AD=AA1,AH⊥平面A1BD,
所以Rt△ABH≌Rt△ADH≌Rt△AA1H,
所以HB=HD=HA1.
又△A1BD是等边三角形,所以点H是△A1BD的中心.
②正确,因为A1B1∥AB,A1B1=AB,CD∥AB,CD=AB,
所以A1B1∥CD,且A1B1=CD,
所以四边形A1B1CD是平行四边形,
所以B1C∥A1D.
又A1D 平面A1BD,B1C 平面A1BD,
所以B1C∥平面A1BD.
同理可证B1D1∥平面A1BD.
又B1C∩B1D1=B1,
所以平面CB1D1∥平面A1BD.
又AH垂直于平面A1BD,所以AH垂直于平面CB1D1.
③正确,连接BC1,AC1,AD1,因为四边形BCC1B1是正方形,
所以B1C⊥BC1.
因为AB⊥平面BCC1B1,B1C 平面BCC1B1,
所以B1C⊥AB.又BC1∩AB=B,
所以B1C⊥平面ABC1D1.
又AC1 平面ABC1D1,
所以AC1⊥B1C,所以直线AC1与直线B1C所成的角是90°.
17、【答案】B
【解析】如图,设AB=a,在平面α内,作AA′⊥l于A′,
则AA′⊥β,连接A′B,则∠ABA′=30°.
在Rt△AA′B中,AB=a,所以AA′=a.
同理作BB′⊥l于B′,连接AB′,则∠BAB′=30°,
所以BB′=a,AB′=a,
所以A′B′==a.
过B作BC綉A′B′,连接A′C,则A′C綉BB′,连接AC.
在Rt△AA′C中,AC==a.
易证BC⊥平面AA′C,所以△ABC为直角三角形,
且AC=BC,所以∠ABC=45°,即l与AB所成的角是45°.
18、【答案】B
【解析】如图所示,取PB的中点O,连接AO,CO,
∵△PAB与△PBC是正三角形,
∴AO⊥PB,CO⊥PB,∵AO∩CO=O,
∴PB⊥平面AOC.∵AC 平面AOC,
∴PB⊥AC,故A成立;
∵△PAB与△PBC是正三角形,∴PA=PC.
设AC∩BD=M,易知M为AC中点,
若PD⊥平面ABCD,则PD⊥BD,
由已知条件知点D满足AC⊥BD且位于BM的延长线上,
∴点D的位置不确定,
即PD与BD不一定垂直,故B不一定成立;
∵AC⊥PB,AC⊥BD,PB∩BD=B,
∴AC⊥平面PBD,∵PD 平面PBD,
∴AC⊥PD,故C成立;
∵AC⊥平面PBD,AC 平面ABCD,
∴平面PBD⊥平面ABCD,故D成立.故选B.
19、【答案】ABC
【解析】因为D,F分别为AB,AC的中点,
所以DF为△ABC的中位线,则BC∥DF,
依据线面平行的判定定理,可知BC∥平面PDF,故A中结论正确;
因为E为BC的中点,且PB=PC,AB=AC,所以BC⊥PE,BC⊥AE,
依据线面垂直的判定定理,可知BC⊥平面PAE,因为BC∥DF,
所以DF⊥平面PAE,故B中结论正确;
因为DF 平面PDF,DF⊥平面PAE,所以平面PDF⊥平面PAE,故C中结论正确;
假设平面PDF⊥平面ABC,则由平面PDF∩平面ABC=DF,AE 平面ABC,
AE⊥DF,DF 平面PDF,得AE⊥平面PDF,所以AE⊥PD,AE⊥PF,
由条件知此垂直关系不一定成立,故D中结论不正确.
20.解:(1)∵AB⊥AD,CD∥AB,∴CD⊥AD,
又PA⊥底面ABCD,CD 平面ABCD,∴PA⊥CD.
又PA∩AD=A,∴CD⊥平面PAD,
又PD 平面PAD,∴CD⊥PD,
∴∠PDA即是二面角P-CD-B的平面角.
又直线PB与CD所成的角为45°,∴∠PBA=45°,∴PA=AB.
∴在Rt△PAD中,PA=AD,∴∠PDA=45°,即二面角P-CD-B的大小为45°.
(2)当点E在线段PC上,且满足PE∶EC=1∶2时,平面EBD⊥平面ABCD.理由如下:
连接AC交BD于点O,连接EO.
由△AOB∽△COD,且CD=2AB,得CO=2AO,
∴PE∶EC=AO∶CO=1∶2,∴PA∥EO.
∵PA⊥底面ABCD,∴EO⊥底面ABCD.
又EO 平面EBD,∴平面EBD⊥平面ABCD.
∴在线段PC上存在点E,满足PE∶EC=1∶2时,平面EBD⊥平面ABCD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
8.6.3 平面与平面垂直(二)
平面与平面垂直的性质
班级 姓名
学习目标
1.掌握平面与平面垂直的性质定理,学会用定理证明垂直关系.
2.熟悉线线垂直、线面垂直、面面垂直间判定和性质的转化.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 平面与平面垂直的性质定理文字语言两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直符号语言图形语言作用①面面垂直 线面垂直 ②作面的垂线【即时训练】(1)(多选题)已知两个平面垂直,下列命题中不正确的是( )A.—个平面内的已知直线必垂直于另—个平面内的任意—条直线B.一个平面内的已知直线必垂直于另一个平面的无数条直线C.一个平面内的任一条直线必垂直于另一个平面D.过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面(2)对于直线m,n和平面α,β,能得出α⊥β的一个条件是( )A.m⊥n,m∥α,n∥β B.m⊥n,α∩β=m,n αC.m∥n,n⊥β,m α D.m∥n,m⊥α,n⊥β
平面与平面垂直的性质定理 例2、如图,P是边长为a的菱形ABCD所在平面外的一点,∠DAB=60°.侧面PAD为正三角形,其所在平面垂直于底面ABCD.(1)若G为AD边的中点,求证:BG⊥平面PAD;(2)求证:AD⊥PB.变式2、如图,在三棱锥P-ABC中,PA⊥平面ABC,平面PAC⊥平面PBC.求证:BC⊥AC.
变式3、如图,M是半圆弧上异于C,D的点,四边形ABCD是矩形,P为AM中点.(1)证明:MC∥平面PBD;(2)若矩形ABCD所在平面与半圆弧所在平面垂直,证明:平面AMD⊥平面BMC.例4、如图,矩形ABCD中,AB=3,BC=3,将C沿BD折至C′,使C′的射影O恰好落在AB上.①求证:BC′⊥平面AC′D;②求A点到平面BC′D的距离.
课后作业
一、基础训练题
1.(多选题)下列命题中正确的是( )
A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ
D.如果平面α⊥平面β,那么平面α内的所有直线都垂直于平面β
2.设平面α⊥平面β,在平面α内的一条直线a垂直于平面β内的一条直线b,则( )
A.直线a必垂直于平面β B.直线b必垂直于平面α
C.直线a不一定垂直于平面β D.过a的平面与过b的平面垂直
3.若平面α⊥平面β,平面β⊥平面γ,则( )
A.α∥γ B.α⊥γ
C.α与γ相交但不垂直 D.以上都有可能
4.《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.
设AA1是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点,
以AA1为底面矩形的一边,则这样的阳马的个数是( )
A.8 B.12 C.16 D.18
5.已知平面α⊥平面β,α∩β=l,点A∈α,A l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是( )
A.AB∥m B.AC⊥m C.AB∥β D.AC⊥β
6.如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )
A.平面ADC⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ABD⊥平面ABC
7.(多选题)如图,点P为四边形ABCD外一点,平面PAD⊥平面ABCD,PA=PD,E为AD的中点,则下列结论不一定成立的是( )
A.PE⊥AC B.PE⊥BC
C.平面PBE⊥平面ABCD
D.平面PBE⊥平面PAD
8.已知α,β是两个不同的平面,l是平面α与β之外的直线,给出下列三个论断:
①l⊥α,②l∥β,③α⊥β.以其中的两个论断作为条件,余下的一个论断作为结论,
写出你认为正确的一个命题:________.(用序号表示)
9.如下左图,△ABC是等腰直角三角形,∠BAC=90°,AB=AC=1,将△ABC沿斜线BC上的高AD折叠,使平面ABD⊥平面ACD,则BC=________.
10.如上右图,空间四边形ABCD中,平面ABD⊥平面BCD,∠BAD=90°,且AB=AD,则AD与平面BCD所成的角是________.
11.已知m,n是两条不相同的直线,α,β是两个不重合的平面,现有以下说法:
①若α∥β,n α,m β,则m∥n;
②若m⊥α,m⊥β,n⊥α,则n⊥β;
③若m⊥n,m⊥α,n⊥β,则α⊥β;
④若m∥α,n∥β,α⊥β,则m⊥n;
⑤若α⊥β,m α,n β,则m⊥n.
其中正确说法的序号有________.
12.如图,已知△ABC为等边三角形,△ABD为等腰直角三角形,AB⊥BD,平面ABC⊥平面ABD,点E与点D在平面ABC的同侧,且CE∥BD,BD=2CE,点F为AD中点,连接EF.
求证:平面AED⊥平面ABD.
13.如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
求证:平面AEC⊥平面AFC.
14.如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E,F分别是棱PC和PD的中点.
(1)求证:EF∥平面PAB;
(2)若AP=AD,且平面PAD⊥平面ABCD,证明:AF⊥平面PCD.
15.如图1,在直角梯形ABCD中,AD∥BC,∠BAD=,AB=BC=AD=a,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1-BCDE.
(1)证明:CD⊥平面A1OC;
(2)当平面A1BE⊥平面BCDE时,四棱锥A1-BCDE的体积为36,求a的值.
二、综合训练题
16.如图,正方体ABCD-A1B1C1D1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,有下面三个结论:
①点H是△A1BD的中心;
②AH垂直于平面CB1D1;
③直线AC1与直线B1C所成的角是90°.
其中正确结论的序号是________.
17.如图,线段AB的两端在直二面角α-l-β的两个面内,并与这两个面都成30°角,则异面直线AB与l所成的角是( )
A.30° B.45°
C.60° D.75°
三、能力提升题
18.如图所示,四棱锥P-ABCD中,△PAB与△PBC是正三角形,
AC⊥BD,则下列结论不一定成立的是( )
A.PB⊥AC
B.PD⊥平面ABCD
C.AC⊥PD
D.平面PBD⊥平面ABCD
19.(多选题)如图,在四面体P ABC中,AB=AC,PB=PC,D,E,F分别是棱AB,BC,CA的中点,则下列结论中一定成立的是( )
A.BC∥平面PDF
B.DF⊥平面PAE
C.平面PDF⊥平面PAE
D.平面PDF⊥平面ABC
20.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AB∥CD,
AB⊥AD,且CD=2AB.
(1)若AB=AD,直线PB与CD所成的角为45°,求二面角P-CD-B的大小;
(2)若E为线段PC上一点,试确定点E的位置,使得平面EBD⊥平面ABCD,并说明理由.
8.6.3 平面与平面垂直(二)
1、【答案】ABC
【解析】平面α⊥平面β,α∩β=l,直线a在平面α内,且a∥l,所以a∥β,所以A正确,D错误.
若平面α内存在垂直于平面β的直线,根据面面垂直的判定定理,有平面α⊥平面β,与前提矛盾,
所以B正确.
设平面α∩平面γ=m,平面β∩平面γ=n,
在平面γ内任取一点A,过该点作c⊥m,d⊥n,且c,d γ.
因为平面α⊥平面γ,平面α∩平面γ=m,c 平面γ,所以c⊥平面α.
又l 平面α,所以l⊥c.同理l⊥d.
因为c∩d=A,所以l⊥平面γ.所以C正确.
2、【答案】C
【解析】当b=α∩β时,必有a⊥β;当b不是α与β的交线时,直线a不一定垂直于平面β.
3、【答案】D
【解析】两个平面都垂直于同一个平面,则这两个平面可能平行,也可能相交,
故A,B,C都有可能.
4、【答案】C
【解析】如图,根据正六边形的性质可知,以四边形A1ABB1,A1AFF1,A1ACC1和A1AEE1为底面矩形,各有4个阳马,故共有4×4=16(个)阳马.故选C.
5、【答案】D
【解析】如图,AB∥l∥m,AC⊥l,m∥α AC⊥m,AB∥l AB∥β. 故选D.
6、【答案】A
解析 易知CD⊥BD,又平面ABD⊥平面BCD,
且平面ABD∩平面BCD=BD,CD 平面BCD,
∴CD⊥平面ABD,又BA 平面ABD,∴CD⊥BA.
又BA⊥AD,且AD∩CD=D,AD,CD 平面ADC,
∴BA⊥平面ADC,又BA 平面ABC,
∴平面ADC⊥平面ABC.
7、【答案】ABC
【解析】因为PA=PD,E为AD的中点,所以PE⊥AD.又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,所以PE⊥平面ABCD,所以PE⊥AC,PE⊥BC,
所以A,B结论一定成立.又PE 平面PBE,所以平面PBE⊥平面ABCD,
所以C结论一定成立.若平面PBE⊥平面PAD,则AD⊥平面PBE,必有AD⊥BE,
此关系不一定成立,故选ABC.
8、【答案】①② ③(答案不唯一)
【解析】由l∥β可在平面β内作l′∥l,又l⊥α,∴l′⊥α,∵l′ β,∴α⊥β,故①② ③.
9、【答案】1
【解析】因为AD⊥BC,所以AD⊥BD,AD⊥CD,
所以∠BDC是二面角B AD C的平面角,
因为平面ABD⊥平面ACD,所以∠BDC=90°.
在△BCD中∠BDC=90°,又AB=AC=1,
所以BD=CD=,所以BC==1.
10、【答案】45°
【解析】如图,过A作AO⊥BD于O 点,∵平面ABD⊥平面BCD,∴AO⊥平面BCD,
则∠ADO即为AD与平面BCD所成的角.∵∠BAD=90°,AB =AD.∴∠ADO=45°.
11、【答案】②③
【解析】对于①,分别位于两个平行平面内的两条直线未必平行,可能是异面直线,因此①不正确;
对于②,由定理“垂直于同一直线的两个平面平行”得α,β平行,由性质“若一条直线垂直于两个平行平面中的一个,则它也垂直于另一个平面”得n⊥β,因此②正确;
对于③,由性质“由空间一点向一个二面角的两个半平面分别引垂线,则这两条垂线所成的角与该二面角相等或互补”得③正确;
对于④,分别平行两个垂直平面的两条直线未必垂直,因此④不正确;对于⑤,m与n还有可能平行或异面,因此⑤不正确.综上所述,说法正确的有②③.
12、【证明】取AB中点O,连接OC,OF.
∵O,F分别为AB,AD中点,则OF∥BD且BD=2OF.
又∵CE∥BD且BD=2CE,
∴CE∥OF且CE=OF,
∴四边形OCEF为平行四边形,∴EF∥OC.
∵△ABC为等边三角形,∴OC⊥AB.
又∵平面ABC⊥平面ABD,且平面ABC∩平面ABD=AB,
∴OC⊥平面ABD.
∵EF∥OC,∴EF⊥平面ABD,又∵EF 平面AED,
∴平面AED⊥平面ABD.
13、【证明】如图,连接BD,设BD交AC于点G,连接EG,FG,EF.
在菱形ABCD中,不妨设GB=1,
由∠ABC=120°,可得AG=GC=.
由BE⊥平面ABCD,AB=BC,可知AE=EC.
又AE⊥EC,所以EG=,且EG⊥AC.
在Rt△EBG中,BE==,故DF=.
在Rt△FDG中,FG==.
在直角梯形BDFE中,由BD=2,BE=,DF=,可得EF=.
因为EG2+FG2=EF2,所以EG⊥FG.
又AC∩FG=G,所以EG⊥平面AFC.
又EG 平面AEC,所以平面AEC⊥平面AFC.
14、【证明】(1)∵E,F分别是棱PC和PD的中点,
∴EF∥CD,
又在矩形ABCD中,AB∥CD,
∴EF∥AB,
∵AB 平面PAB,EF 平面PAB,
∴EF∥平面PAB.
(2)在矩形ABCD中,AD⊥CD,
又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,CD 平面ABCD,
∴CD⊥平面PAD,
又AF 平面PAD,∴CD⊥AF.
∵PA=AD,F是PD的中点,∴AF⊥PD,
∵PD 平面PCD,CD 平面PCD,PD∩CD=D,∴AF⊥平面PCD.
15、【解】①证明:在题图1中,由已知条件易得BE⊥AC,
即在题图2中,BE⊥A1O,BE⊥OC,
又A1O∩OC=O,∴BE⊥平面A1OC.
易知四边形BCDE是平行四边形,
∴BE∥CD,∴CD⊥平面A1OC.
②已知平面A1BE⊥平面BCDE,且平面A1BE∩平面BCDE=BE.
又由①知,A1O⊥BE,
∴A1O⊥平面BCDE,即A1O是四棱锥A1-BCDE的高.
易知A1O=a,S四边形BCDE=a·a=a2,
从而四棱锥A1-BCDE的体积V=×S四边形BCDE×A1O=×a2×a=a3=36,解得a=6.
16、【答案】①②③
【解析】①正确,连接A1H,BH,DH.
因为AB=AD=AA1,AH⊥平面A1BD,
所以Rt△ABH≌Rt△ADH≌Rt△AA1H,
所以HB=HD=HA1.
又△A1BD是等边三角形,所以点H是△A1BD的中心.
②正确,因为A1B1∥AB,A1B1=AB,CD∥AB,CD=AB,
所以A1B1∥CD,且A1B1=CD,
所以四边形A1B1CD是平行四边形,
所以B1C∥A1D.
又A1D 平面A1BD,B1C 平面A1BD,
所以B1C∥平面A1BD.
同理可证B1D1∥平面A1BD.
又B1C∩B1D1=B1,
所以平面CB1D1∥平面A1BD.
又AH垂直于平面A1BD,所以AH垂直于平面CB1D1.
③正确,连接BC1,AC1,AD1,因为四边形BCC1B1是正方形,
所以B1C⊥BC1.
因为AB⊥平面BCC1B1,B1C 平面BCC1B1,
所以B1C⊥AB.又BC1∩AB=B,
所以B1C⊥平面ABC1D1.
又AC1 平面ABC1D1,
所以AC1⊥B1C,所以直线AC1与直线B1C所成的角是90°.
17、【答案】B
【解析】如图,设AB=a,在平面α内,作AA′⊥l于A′,
则AA′⊥β,连接A′B,则∠ABA′=30°.
在Rt△AA′B中,AB=a,所以AA′=a.
同理作BB′⊥l于B′,连接AB′,则∠BAB′=30°,
所以BB′=a,AB′=a,
所以A′B′==a.
过B作BC綉A′B′,连接A′C,则A′C綉BB′,连接AC.
在Rt△AA′C中,AC==a.
易证BC⊥平面AA′C,所以△ABC为直角三角形,
且AC=BC,所以∠ABC=45°,即l与AB所成的角是45°.
18、【答案】B
【解析】如图所示,取PB的中点O,连接AO,CO,
∵△PAB与△PBC是正三角形,
∴AO⊥PB,CO⊥PB,∵AO∩CO=O,
∴PB⊥平面AOC.∵AC 平面AOC,
∴PB⊥AC,故A成立;
∵△PAB与△PBC是正三角形,∴PA=PC.
设AC∩BD=M,易知M为AC中点,
若PD⊥平面ABCD,则PD⊥BD,
由已知条件知点D满足AC⊥BD且位于BM的延长线上,
∴点D的位置不确定,
即PD与BD不一定垂直,故B不一定成立;
∵AC⊥PB,AC⊥BD,PB∩BD=B,
∴AC⊥平面PBD,∵PD 平面PBD,
∴AC⊥PD,故C成立;
∵AC⊥平面PBD,AC 平面ABCD,
∴平面PBD⊥平面ABCD,故D成立.故选B.
19、【答案】ABC
【解析】因为D,F分别为AB,AC的中点,
所以DF为△ABC的中位线,则BC∥DF,
依据线面平行的判定定理,可知BC∥平面PDF,故A中结论正确;
因为E为BC的中点,且PB=PC,AB=AC,所以BC⊥PE,BC⊥AE,
依据线面垂直的判定定理,可知BC⊥平面PAE,因为BC∥DF,
所以DF⊥平面PAE,故B中结论正确;
因为DF 平面PDF,DF⊥平面PAE,所以平面PDF⊥平面PAE,故C中结论正确;
假设平面PDF⊥平面ABC,则由平面PDF∩平面ABC=DF,AE 平面ABC,
AE⊥DF,DF 平面PDF,得AE⊥平面PDF,所以AE⊥PD,AE⊥PF,
由条件知此垂直关系不一定成立,故D中结论不正确.
20.解:(1)∵AB⊥AD,CD∥AB,∴CD⊥AD,
又PA⊥底面ABCD,CD 平面ABCD,∴PA⊥CD.
又PA∩AD=A,∴CD⊥平面PAD,
又PD 平面PAD,∴CD⊥PD,
∴∠PDA即是二面角P-CD-B的平面角.
又直线PB与CD所成的角为45°,∴∠PBA=45°,∴PA=AB.
∴在Rt△PAD中,PA=AD,∴∠PDA=45°,即二面角P-CD-B的大小为45°.
(2)当点E在线段PC上,且满足PE∶EC=1∶2时,平面EBD⊥平面ABCD.理由如下:
连接AC交BD于点O,连接EO.
由△AOB∽△COD,且CD=2AB,得CO=2AO,
∴PE∶EC=AO∶CO=1∶2,∴PA∥EO.
∵PA⊥底面ABCD,∴EO⊥底面ABCD.
又EO 平面EBD,∴平面EBD⊥平面ABCD.
∴在线段PC上存在点E,满足PE∶EC=1∶2时,平面EBD⊥平面ABCD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
