平面向量数量积的物理背景及其含义
文档属性
| 名称 | 平面向量数量积的物理背景及其含义 |

|
|
| 格式 | rar | ||
| 文件大小 | 251.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-01 00:00:00 | ||
图片预览



文档简介
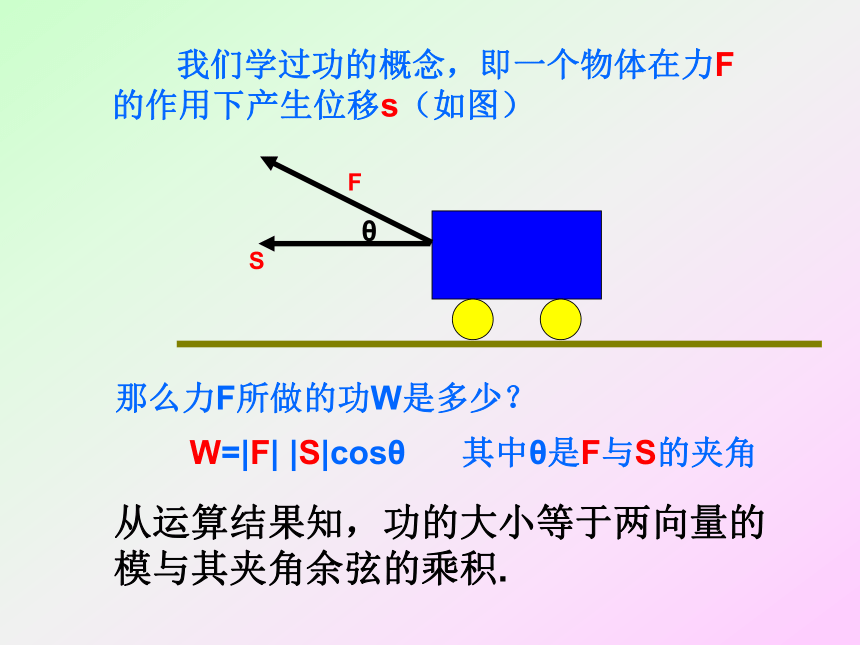
课件18张PPT。平面向量的数量积平面向量数量积的物理背景及其含义冷水江一中 李芳桂 我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)θFS那么力F所做的功W是多少?
W=|F| |S|cosθ 其中θ是F与S的夹角从运算结果知,功的大小等于两向量的模与其夹角余弦的乘积.定
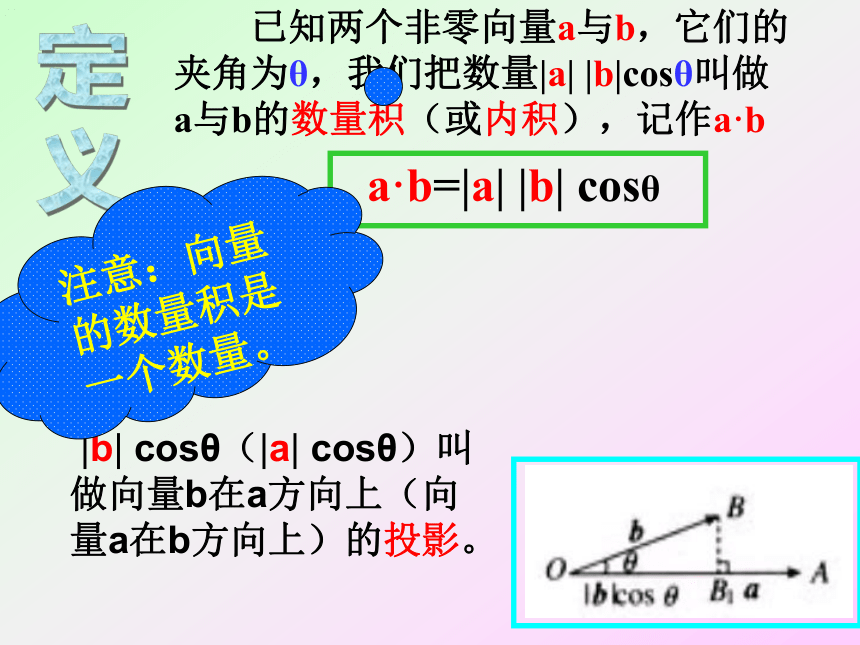
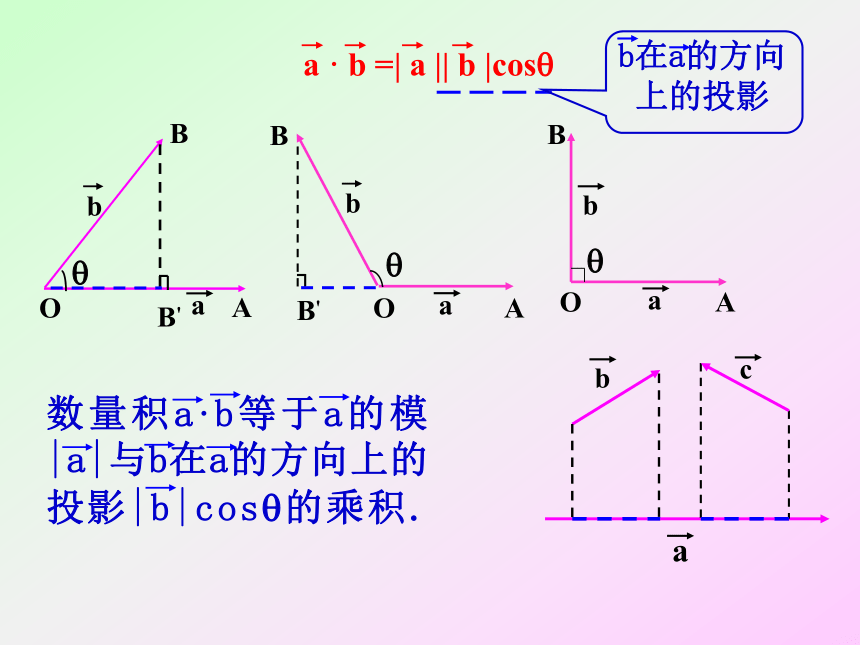
义 |b| cosθ(|a| cosθ)叫做向量b在a方向上(向量a在b方向上)的投影。注意:向量的数量积是一个数量。
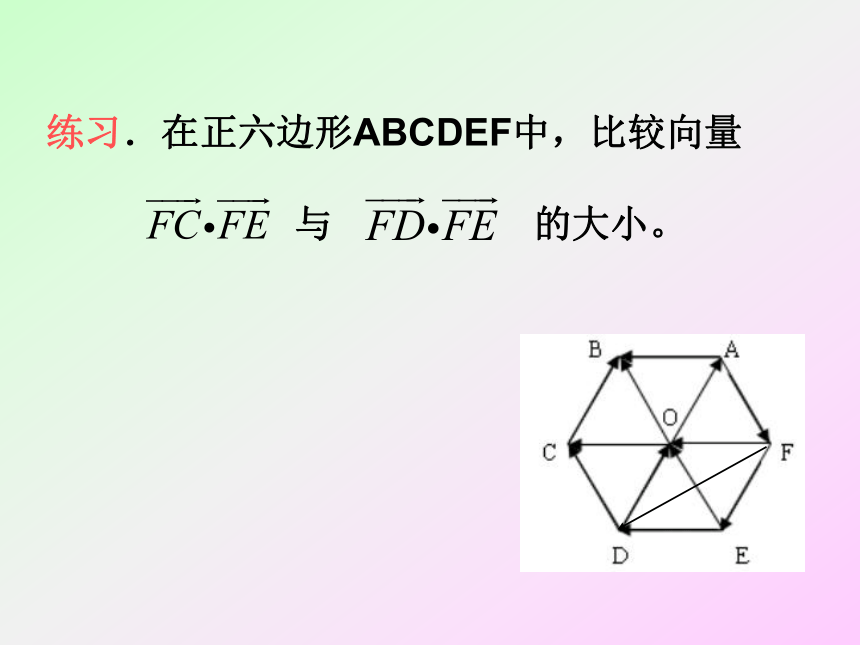
练习.在正六边形ABCDEF中,比较向量
与 的大小。
线性运算与向量的数量积运算的结果有什么不同?影响数量积大小的因素有哪些?
答:线性运算的结果是向量,而数量积的结果则是数量,这个数量的大小不仅和向量 与
的模有关,还和它们的夹角有关,数量积运算结果的符号取决于向量 与 的夹角 。
请同学们完成下表>=<重要性质:特别地例1 在△ABC中a=5,b=8,C=60o,
求回顾实数运算中有关的运算律,类比数量积得运算律,体会不同运算的运算律不尽相同 在实数中 在向量运算中
交换律: ab=ba ( )
结合律: (ab)c=a(bc) ( )
( )
分配律: (a+b)c=ab+bc ( )
消去律: ab=bc(b≠0) a=c
( )√√√ × × 则
(a + b) ·c = ON |c|
= (OM + MN) |c|
= OM|c| + MN|c|
= a·c + b·c . ONMa+bbac 向量a、b、a + b在c上的射影的数量分别是OM、MN、 ON, 证明运算律(3)数量积的运算律:例 2:求证:(结论)(1)(a+b)2=a2+2a·b+b2;(2)(a+b)·(a-b)=a2-b2.证明:(1)(a+b)2=(a+b)·(a+b)=(a+b)·a+(a+b)·b=a·a+b·a+a·b+b·b=a2+2a·b+b2.证明:(2)(a+b)·(a-b)=(a+b)·a-(a+b)·b
=a·a+b·a-a·b-b·b
=a2-b2.解:a+kb与a-kb互相垂直的条件是
( a+kb)· (a-kb)=0
即a·a-k·k·b·b=0
9-16 =0
所以,k= EX:谢 谢 指 导!
再 见
W=|F| |S|cosθ 其中θ是F与S的夹角从运算结果知,功的大小等于两向量的模与其夹角余弦的乘积.定
义 |b| cosθ(|a| cosθ)叫做向量b在a方向上(向量a在b方向上)的投影。注意:向量的数量积是一个数量。
练习.在正六边形ABCDEF中,比较向量
与 的大小。
线性运算与向量的数量积运算的结果有什么不同?影响数量积大小的因素有哪些?
答:线性运算的结果是向量,而数量积的结果则是数量,这个数量的大小不仅和向量 与
的模有关,还和它们的夹角有关,数量积运算结果的符号取决于向量 与 的夹角 。
请同学们完成下表>=<重要性质:特别地例1 在△ABC中a=5,b=8,C=60o,
求回顾实数运算中有关的运算律,类比数量积得运算律,体会不同运算的运算律不尽相同 在实数中 在向量运算中
交换律: ab=ba ( )
结合律: (ab)c=a(bc) ( )
( )
分配律: (a+b)c=ab+bc ( )
消去律: ab=bc(b≠0) a=c
( )√√√ × × 则
(a + b) ·c = ON |c|
= (OM + MN) |c|
= OM|c| + MN|c|
= a·c + b·c . ONMa+bbac 向量a、b、a + b在c上的射影的数量分别是OM、MN、 ON, 证明运算律(3)数量积的运算律:例 2:求证:(结论)(1)(a+b)2=a2+2a·b+b2;(2)(a+b)·(a-b)=a2-b2.证明:(1)(a+b)2=(a+b)·(a+b)=(a+b)·a+(a+b)·b=a·a+b·a+a·b+b·b=a2+2a·b+b2.证明:(2)(a+b)·(a-b)=(a+b)·a-(a+b)·b
=a·a+b·a-a·b-b·b
=a2-b2.解:a+kb与a-kb互相垂直的条件是
( a+kb)· (a-kb)=0
即a·a-k·k·b·b=0
9-16 =0
所以,k= EX:谢 谢 指 导!
再 见
