沪教版八年级数学上册试题 第19章 《几何证明》单元测试卷(含解析)
文档属性
| 名称 | 沪教版八年级数学上册试题 第19章 《几何证明》单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 539.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 00:00:00 | ||
图片预览




文档简介
第19章 《几何证明》单元测试卷
一、单选题(共18分)
1.下列说法正确的是( )
A.一个命题一定有逆命题 B.一个定理一定有逆定理
C.真命题的逆命题一定是真命题 D.假命题的逆命题一定是假命题
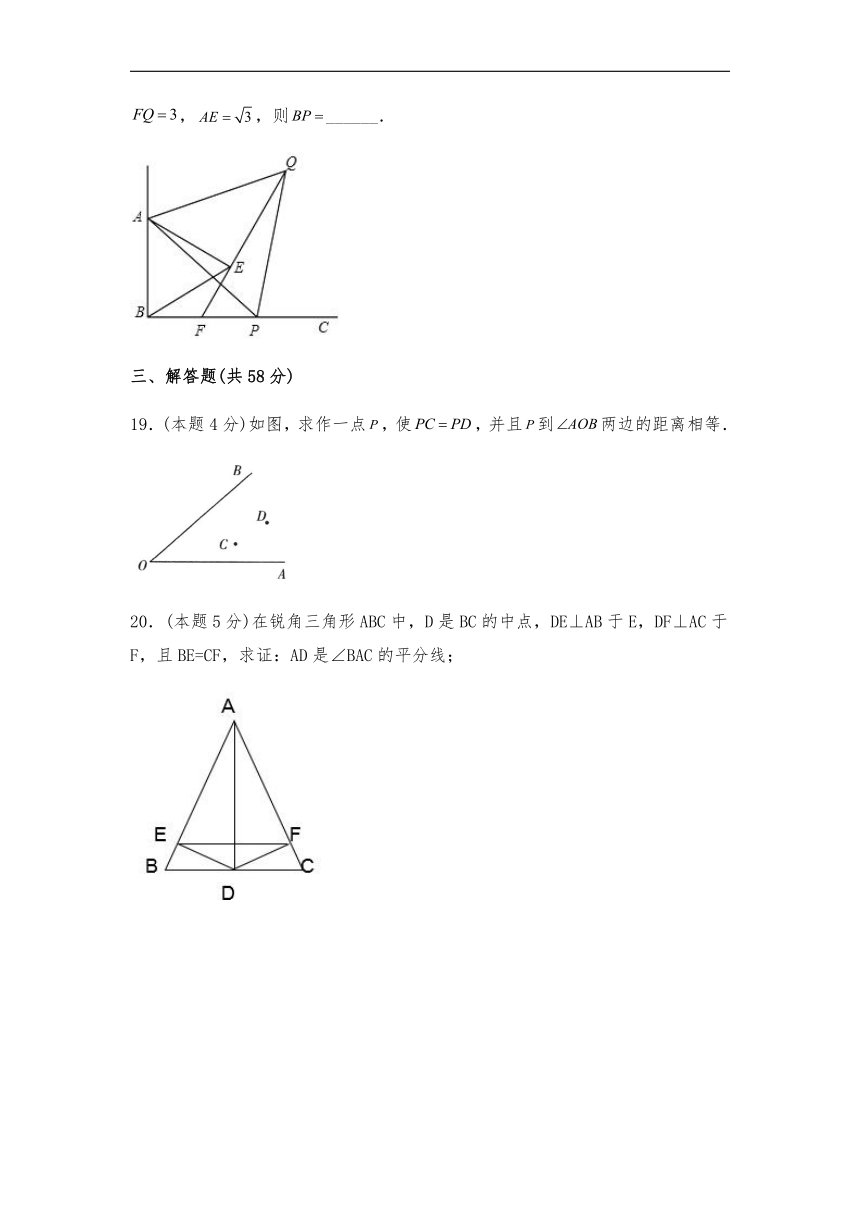
2.下列命题是真命题的是( ).
A.经过直线外一点有且只有一条直线与已知直线平行
B.两条直线被第三条直线所截,同位角相等
C.相等的两个角是对顶角
D.从直线外一点到这条直线的垂线段,叫做这点到直线的距离
3.下列说法:①有两条直角边对应相等的两个直角三角形全等;②有斜边对应相等的两个等腰直角三角形全等;③有一条直角边和斜边上的高对应相等的两个直角三角形全等;④有一条边相等的两个等腰直角三角形全等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,是等腰直角三角形,点在边上,且,则是( ).
A. B. C. D.
5.如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
A.48° B.36° C.30° D.24°
6.如图,是的中线,,将沿直线翻折,点落在点的位置上,如果,求的长为( ).
A.10 B.5 C. D.
二、填空题(共24分)
7.将命题“同角的补角相等”改写成“如果……,那么……”的形式为_________________.
8.命题:直角三角形两条直角边的平方和等于斜边的平方,其逆命题是_____________.
9.如果等腰三角形腰上的高是腰长的一半,那么它顶角的度数是_____.
10.到定点的跑离为的点的轨迹是__ ____.
11.如图,∠A=∠D=90°,请添加一个条件:______,使得△ABC≌△DCB.
12.如图,在Rt△ABC中,∠B=90°,CD平分∠ACB,过点D作DE⊥AC于点E,若AE=4,AB=10,则△ADE的周长为________ .
13.如果一个三角形的三条边长分别为、、,那么这个三角形的面积为______.
14.已知点、,则线段的长为______.
15.已知等腰三角形的腰长为5,一腰上的高为3,则以底边为边长的正方形的面积为________
16.在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是____.
17.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为________.
18.如图,,P为射线上任意一点(点P和点B不重合),分别以,为边在内部作等边和等边,连结并延长交于点F,若,,则______.
三、解答题(共58分)
19.(本题4分)如图,求作一点,使,并且到两边的距离相等.
20.(本题5分)在锐角三角形ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,且BE=CF,求证:AD是∠BAC的平分线;
21.(本题5分)已知的三个顶点分别是、、,试判断的形状.
22.(本题5分)如图,为了测量旗杆AB的高度,可以利用从旗杆顶端垂下的绳子,当绳子垂直地面时,量得绳子比旗杆多1m,将绳子拉直到地面的C点,测得CB的长为5m,求旗杆AB的高度.
23.(本题5分)(1)证明:“三角形内角和是180°”;
(2)请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,判断这一逆命题是真命题还是假命题,如果是真命题给出证明,如果是假命题,说明理由.
24.(本题5分)如图,已知,.求证:.
25.(本题6分)教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4×ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,则斜边AB上的高CD的长为多少
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2 , 画在如图4的网格中,并标出字母a、b所表示的线段.
26.(本题6分)如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
27.(本题8分)已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)
28.(本题9分)如图,在中,,,,点、、分别在边、、上(点、与顶点不重合),平分,,垂足为.
(1)求证:;
(2)设,,求与之间的函数解析式;
(3)当时,求出的长.
答案
一、单选题
1.A
【解析】
解:A、每个命题都有逆命题,故本选项正确.
B、每个定理不一定都有逆定理,故本选项错误.
C、真命题的逆命题不一定是真命题,故本选项错误.
D、假命题的逆命题不一定是假命题,故本选项错误.
故选A.
2.A
【解析】
A、经过直线外一点,有且只有一条直线与这条直线平行,正确,是真命题;
B、两条平行直线被第三条直线所截,同位角相等,故错误,是假命题;
C、相等的两个角不一定是对顶角,故错误,是假命题;
D、从直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离,故错误,是假命题;
故选A.
3.C
【解析】
因为有两条直角边对应相等的两个直角三角形可利用SAS判定两个直角三角形全等,所以①正确,
因为有斜边对应相等的两个等腰直角三角形可以利用ASA判定两三角形全等,所以②正确,
因为有一条直角边和斜边上的高对应相等可以先判定直角边与高线所在的两个三角形全等,继而可得角相等,然后利用ASA即可判定两个直角三角形全等,所以③正确,
有一条边相等的两个等腰直角三角形无法判定两个直角三角形全等,所以④错误,
故选C.
4.C
【解析】
∵是等腰直角三角形,
∴∠ABC=∠ACB=45°,∠BAC=90°,
∵,
∴∠ABD=30°,
∴=∠ABC-∠ABD=15°,
故选C.
5.A
【解析】∵BD平分∠ABC,∴∠DBC=∠ABD=24°,∵∠A=60°,∴∠ACB=180°﹣60°﹣24°×2=72°,∵BC的中垂线交BC于点E,∴BF=CF,∴∠FCB=24°,∴∠ACF=72°﹣24°=48°,故选A.
6.C
【解析】
∵把△ABC沿直线AD折过来,点C落在点C′的位置,
∴△ADC≌△ADC′,
∴∠ADC=∠ADC′=45°,DC=DC′=BD,
∴△BDC′是等腰直角三角形,且直角边为5,
那么斜边BC′=.
故选C.
二、填空题
7.如果两个角是同一个角的补角,那么这两个角相等
【解析】如果两个角是同一个角的补角,那么这两个角相等
8.如果三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
【解析】
解:因为原命题的题设是“一个三角形是直角三角形”,结论是“两条直角边的平方和等于斜边的平方”,
所以“直角三角形两条直角边的平方和等于斜边的平方”的逆命题是“如果三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形”.
9.30°或150°.
【解析】
解:①如图,△ABC中,AB=AC,CD⊥AB且CD=AB,
∵△ABC中,CD⊥AB且CD=AB,AB=AC,
∴CD=AC,
∴∠A=30°.
②如图,△ABC中,AB=AC,CD⊥BA的延长线于点D,且CD=AB,
∵∠CDA=90°,CD=AB,AB=AC,
∴CD=AC,
∴∠DAC=30°,
∴∠A=150°.
故答案为30°或150°.
10.以点为圆心,为半径的圆
【解析】
到定点A的距离为9cm的点的轨迹是:以A为圆心,以9cm为半径的圆.
故答案是:以A为圆心,以9cm为半径的圆.
11.∠ABC=∠DCB.
【解析】
解:因为∠A=∠D=90°,BC=CB,∠ABC=∠DCB,所以△ABC≌△DCB,故条件成立
12.14
【解析】
∵CD平分∠ACB,∠B=90°,DE⊥AC,
∴BD=DE,
∴AD+DB=AD+DE=AB=10,
∴△ADE的周长=AD+DE+AE=10+4=14.
故答案为:14.
13.30
【解析】
∵52+122=132,
∴此三角形是直角三角形,
∴×5×12=30,
故答案为30.
14.10
【解析】
线段PQ的长= =10.
故答案为10.
15.10或90
【解析】
根据题意作出图形分为高线在三角形内和高线在三角形外两种情况:
如图1,AC=5,CD=3,CD⊥AB,根据勾股定理可知:AD==4,
∴BD=1.
∴BC2=12+32=10.
如图2,AC=5,CD=3,CD⊥AB,根据勾股定理可知:AD==4,
∴BD=9,
∴BC2=92+32=90.
故答案是:10或90.
16.15
【解析】
已知,∠A=50°,AB=AC ∠ABC=∠ACB=65°
又∵DE垂直且平分AB DB=AD
∴∠ABD=∠A=50°
∴∠DBC=∠ABC-∠ABD=65°-50°=15°.
故答案为15.
17.4
【解析】
∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∵BD平分∠ABC,
∴∠DBA=30°,
∴∠A=∠DBA,
∴AD=BD=8,
∵P点是BD的中点,∠ACB=90°,
∴CP=BD=4,
故答案为:4.
18.2
【解析】
解:如图:连接,过点E作,
∵,是等边三角形,
∴,,,
∴且,,
∴,
∴,,
∴,,
∴,
∴,,
∵,
∴,
∴,,
∵,,
∴,,
∵,
∴,,
∵
∴,,
∵
∴,
∴,
故答案为2.
三、解答题
19.
解:
点P就是所求的点.
20.
证明:∵D是BC的中点,
∴BD=DC,
∵DE⊥AB于E,DF⊥AC于F,
∴△BED与△CFD都是直角三角形,
又BE=CF,
∴RT△BED≌RT△CFD(HL),
∴DE=DF,
∴AD是∠BAC的平分线(角平分线的判定定理).
21.
,
,
,得.
∵,,∴.得.
∴是等腰直角三角形.
22.
设旗杆AB的高度为xm,则AC=(x+1)m,
在Rt△ABC中,由勾股定理得,
AB2+BC2=AC2
即52+x2=(x+1)2
解得:x=12.
答:旗杆AB的高度为12m.
23.
(1)证明:已知:△ABC, 求证:∠BAC+∠B+∠C=180°,
证明:过点A作EF∥BC,
∵EF∥BC,
∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,
∴∠BAC+∠B+∠C=180°.
即知三角形内角和等于180°
(2)解:“直角三角形斜边上的中线等于斜边的一半”的逆命题是一个三角形一边上的中线是这边的一半,那么这个三角形是直角三角形,是真命题. 已知,如图,△ABC中,D是AB边的中点,且CD= AB
求证:△ABC是直角三角形,
证明:∵D是AB边的中点,且CD= AB,
∴AD=BD=CD,
∵AD=CD,
∴∠ACD=∠A,
∵BD=CD,
∴∠BCD=∠B,
又∵∠ACD+∠BCD+∠A+∠B=180°,
∴2(∠ACD+∠BCD)=180°,
∴∠ACD+∠BCD=90°,
∴∠ACB=90°,
∴△ABC是直角三角形.
24.
连接,
∵,
∴△DBC为等腰三角形,
∴.
∵,
∴.
∴.
25.
解:(1)梯形ABCD的面积为(a+b)(a+b)=a2+ab+b2 ,
也利用表示为ab+c2+ab,
∴a2+ab+b2=ab+c2+ab,即a2+b2=c2
(2)∵直角三角形的两直角边分别为3,4,
∴斜边为5,
∵设斜边上的高为h,直角三角形的面积为×3×4=×5×h,
∴h=.
(3)∵图形面积为:(a+b)(a+2b)=a2+3ab+2b2 ,
∴边长为(a+2b)(a+b),
由此可画出的图形为:
26.
(1)证明:∵EF是AD的垂直平分线,
∴AF=DF.
∴∠FAD=∠FDA.
(2)∵AD平分∠BAC,
∴∠BAD=∠DAC.
∵∠FDA=∠BAD+∠B,∠FAD=∠DAC+∠CAF,
由(1)知∠FAD=∠FDA,
∴∠B=∠CAF.
∵∠B=50°,
∴∠CAF=50°.
27.
(1)结论:AE2+BF2=EF2 .
理由:如图1中,延长FD到M,使得DM=DF,连接AM,EM.
在△ADM和△BDF中,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2 ,
∴AE2+BF2=EF2 .
(2)如图2中,结论不变.AE2+BF2=EF2
理由:延长FD到M,使得DM=DF,连接AM,EM.
在△ADM和△BDF中,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=∠CAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2 ,
∴AE2+BF2=EF2 .
28.
(1)证明:在△ABC中,∵∠C=90°,∠B=30°,
∴∠CAB=60°,
又∵AD平分∠CAB,
∴∠DAB=∠DAC=∠CAB=30°,
∴∠DAB=∠B,
∴AD=DB.
(2)解:在△AEF中,∵∠AFE=90°,∠EAF=60°,
∴∠AEF=30°,
∴AE=AC-EC=6-x,AF=AE= (6 x),
在Rt△ABC中,∵∠B=30°,AC=6,
∴AB=12,
∴BF=AB-AF=12- (6 x)=9+x,
∴y=9+x,
答:y关于x的函数解析式是y=9+x(0<x<6).
(3)解:当∠DEF=90°时,∠CED=180°-∠AEF-∠FED=60°,
∴∠EDC=30°,ED=2x,
∵∠C=90°,∠DAC=30°,
∴∠ADC=60°,
∴∠EDA=60°-30°=30°=∠DAE,
∴ED=AE=6-x.
∴有2x=6-x,得x=2,
此时,y=9+×2=10,
答:BF的长为10.
一、单选题(共18分)
1.下列说法正确的是( )
A.一个命题一定有逆命题 B.一个定理一定有逆定理
C.真命题的逆命题一定是真命题 D.假命题的逆命题一定是假命题
2.下列命题是真命题的是( ).
A.经过直线外一点有且只有一条直线与已知直线平行
B.两条直线被第三条直线所截,同位角相等
C.相等的两个角是对顶角
D.从直线外一点到这条直线的垂线段,叫做这点到直线的距离
3.下列说法:①有两条直角边对应相等的两个直角三角形全等;②有斜边对应相等的两个等腰直角三角形全等;③有一条直角边和斜边上的高对应相等的两个直角三角形全等;④有一条边相等的两个等腰直角三角形全等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,是等腰直角三角形,点在边上,且,则是( ).
A. B. C. D.
5.如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
A.48° B.36° C.30° D.24°
6.如图,是的中线,,将沿直线翻折,点落在点的位置上,如果,求的长为( ).
A.10 B.5 C. D.
二、填空题(共24分)
7.将命题“同角的补角相等”改写成“如果……,那么……”的形式为_________________.
8.命题:直角三角形两条直角边的平方和等于斜边的平方,其逆命题是_____________.
9.如果等腰三角形腰上的高是腰长的一半,那么它顶角的度数是_____.
10.到定点的跑离为的点的轨迹是__ ____.
11.如图,∠A=∠D=90°,请添加一个条件:______,使得△ABC≌△DCB.
12.如图,在Rt△ABC中,∠B=90°,CD平分∠ACB,过点D作DE⊥AC于点E,若AE=4,AB=10,则△ADE的周长为________ .
13.如果一个三角形的三条边长分别为、、,那么这个三角形的面积为______.
14.已知点、,则线段的长为______.
15.已知等腰三角形的腰长为5,一腰上的高为3,则以底边为边长的正方形的面积为________
16.在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是____.
17.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为________.
18.如图,,P为射线上任意一点(点P和点B不重合),分别以,为边在内部作等边和等边,连结并延长交于点F,若,,则______.
三、解答题(共58分)
19.(本题4分)如图,求作一点,使,并且到两边的距离相等.
20.(本题5分)在锐角三角形ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,且BE=CF,求证:AD是∠BAC的平分线;
21.(本题5分)已知的三个顶点分别是、、,试判断的形状.
22.(本题5分)如图,为了测量旗杆AB的高度,可以利用从旗杆顶端垂下的绳子,当绳子垂直地面时,量得绳子比旗杆多1m,将绳子拉直到地面的C点,测得CB的长为5m,求旗杆AB的高度.
23.(本题5分)(1)证明:“三角形内角和是180°”;
(2)请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,判断这一逆命题是真命题还是假命题,如果是真命题给出证明,如果是假命题,说明理由.
24.(本题5分)如图,已知,.求证:.
25.(本题6分)教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4×ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,则斜边AB上的高CD的长为多少
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2 , 画在如图4的网格中,并标出字母a、b所表示的线段.
26.(本题6分)如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
27.(本题8分)已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)
28.(本题9分)如图,在中,,,,点、、分别在边、、上(点、与顶点不重合),平分,,垂足为.
(1)求证:;
(2)设,,求与之间的函数解析式;
(3)当时,求出的长.
答案
一、单选题
1.A
【解析】
解:A、每个命题都有逆命题,故本选项正确.
B、每个定理不一定都有逆定理,故本选项错误.
C、真命题的逆命题不一定是真命题,故本选项错误.
D、假命题的逆命题不一定是假命题,故本选项错误.
故选A.
2.A
【解析】
A、经过直线外一点,有且只有一条直线与这条直线平行,正确,是真命题;
B、两条平行直线被第三条直线所截,同位角相等,故错误,是假命题;
C、相等的两个角不一定是对顶角,故错误,是假命题;
D、从直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离,故错误,是假命题;
故选A.
3.C
【解析】
因为有两条直角边对应相等的两个直角三角形可利用SAS判定两个直角三角形全等,所以①正确,
因为有斜边对应相等的两个等腰直角三角形可以利用ASA判定两三角形全等,所以②正确,
因为有一条直角边和斜边上的高对应相等可以先判定直角边与高线所在的两个三角形全等,继而可得角相等,然后利用ASA即可判定两个直角三角形全等,所以③正确,
有一条边相等的两个等腰直角三角形无法判定两个直角三角形全等,所以④错误,
故选C.
4.C
【解析】
∵是等腰直角三角形,
∴∠ABC=∠ACB=45°,∠BAC=90°,
∵,
∴∠ABD=30°,
∴=∠ABC-∠ABD=15°,
故选C.
5.A
【解析】∵BD平分∠ABC,∴∠DBC=∠ABD=24°,∵∠A=60°,∴∠ACB=180°﹣60°﹣24°×2=72°,∵BC的中垂线交BC于点E,∴BF=CF,∴∠FCB=24°,∴∠ACF=72°﹣24°=48°,故选A.
6.C
【解析】
∵把△ABC沿直线AD折过来,点C落在点C′的位置,
∴△ADC≌△ADC′,
∴∠ADC=∠ADC′=45°,DC=DC′=BD,
∴△BDC′是等腰直角三角形,且直角边为5,
那么斜边BC′=.
故选C.
二、填空题
7.如果两个角是同一个角的补角,那么这两个角相等
【解析】如果两个角是同一个角的补角,那么这两个角相等
8.如果三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
【解析】
解:因为原命题的题设是“一个三角形是直角三角形”,结论是“两条直角边的平方和等于斜边的平方”,
所以“直角三角形两条直角边的平方和等于斜边的平方”的逆命题是“如果三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形”.
9.30°或150°.
【解析】
解:①如图,△ABC中,AB=AC,CD⊥AB且CD=AB,
∵△ABC中,CD⊥AB且CD=AB,AB=AC,
∴CD=AC,
∴∠A=30°.
②如图,△ABC中,AB=AC,CD⊥BA的延长线于点D,且CD=AB,
∵∠CDA=90°,CD=AB,AB=AC,
∴CD=AC,
∴∠DAC=30°,
∴∠A=150°.
故答案为30°或150°.
10.以点为圆心,为半径的圆
【解析】
到定点A的距离为9cm的点的轨迹是:以A为圆心,以9cm为半径的圆.
故答案是:以A为圆心,以9cm为半径的圆.
11.∠ABC=∠DCB.
【解析】
解:因为∠A=∠D=90°,BC=CB,∠ABC=∠DCB,所以△ABC≌△DCB,故条件成立
12.14
【解析】
∵CD平分∠ACB,∠B=90°,DE⊥AC,
∴BD=DE,
∴AD+DB=AD+DE=AB=10,
∴△ADE的周长=AD+DE+AE=10+4=14.
故答案为:14.
13.30
【解析】
∵52+122=132,
∴此三角形是直角三角形,
∴×5×12=30,
故答案为30.
14.10
【解析】
线段PQ的长= =10.
故答案为10.
15.10或90
【解析】
根据题意作出图形分为高线在三角形内和高线在三角形外两种情况:
如图1,AC=5,CD=3,CD⊥AB,根据勾股定理可知:AD==4,
∴BD=1.
∴BC2=12+32=10.
如图2,AC=5,CD=3,CD⊥AB,根据勾股定理可知:AD==4,
∴BD=9,
∴BC2=92+32=90.
故答案是:10或90.
16.15
【解析】
已知,∠A=50°,AB=AC ∠ABC=∠ACB=65°
又∵DE垂直且平分AB DB=AD
∴∠ABD=∠A=50°
∴∠DBC=∠ABC-∠ABD=65°-50°=15°.
故答案为15.
17.4
【解析】
∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∵BD平分∠ABC,
∴∠DBA=30°,
∴∠A=∠DBA,
∴AD=BD=8,
∵P点是BD的中点,∠ACB=90°,
∴CP=BD=4,
故答案为:4.
18.2
【解析】
解:如图:连接,过点E作,
∵,是等边三角形,
∴,,,
∴且,,
∴,
∴,,
∴,,
∴,
∴,,
∵,
∴,
∴,,
∵,,
∴,,
∵,
∴,,
∵
∴,,
∵
∴,
∴,
故答案为2.
三、解答题
19.
解:
点P就是所求的点.
20.
证明:∵D是BC的中点,
∴BD=DC,
∵DE⊥AB于E,DF⊥AC于F,
∴△BED与△CFD都是直角三角形,
又BE=CF,
∴RT△BED≌RT△CFD(HL),
∴DE=DF,
∴AD是∠BAC的平分线(角平分线的判定定理).
21.
,
,
,得.
∵,,∴.得.
∴是等腰直角三角形.
22.
设旗杆AB的高度为xm,则AC=(x+1)m,
在Rt△ABC中,由勾股定理得,
AB2+BC2=AC2
即52+x2=(x+1)2
解得:x=12.
答:旗杆AB的高度为12m.
23.
(1)证明:已知:△ABC, 求证:∠BAC+∠B+∠C=180°,
证明:过点A作EF∥BC,
∵EF∥BC,
∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,
∴∠BAC+∠B+∠C=180°.
即知三角形内角和等于180°
(2)解:“直角三角形斜边上的中线等于斜边的一半”的逆命题是一个三角形一边上的中线是这边的一半,那么这个三角形是直角三角形,是真命题. 已知,如图,△ABC中,D是AB边的中点,且CD= AB
求证:△ABC是直角三角形,
证明:∵D是AB边的中点,且CD= AB,
∴AD=BD=CD,
∵AD=CD,
∴∠ACD=∠A,
∵BD=CD,
∴∠BCD=∠B,
又∵∠ACD+∠BCD+∠A+∠B=180°,
∴2(∠ACD+∠BCD)=180°,
∴∠ACD+∠BCD=90°,
∴∠ACB=90°,
∴△ABC是直角三角形.
24.
连接,
∵,
∴△DBC为等腰三角形,
∴.
∵,
∴.
∴.
25.
解:(1)梯形ABCD的面积为(a+b)(a+b)=a2+ab+b2 ,
也利用表示为ab+c2+ab,
∴a2+ab+b2=ab+c2+ab,即a2+b2=c2
(2)∵直角三角形的两直角边分别为3,4,
∴斜边为5,
∵设斜边上的高为h,直角三角形的面积为×3×4=×5×h,
∴h=.
(3)∵图形面积为:(a+b)(a+2b)=a2+3ab+2b2 ,
∴边长为(a+2b)(a+b),
由此可画出的图形为:
26.
(1)证明:∵EF是AD的垂直平分线,
∴AF=DF.
∴∠FAD=∠FDA.
(2)∵AD平分∠BAC,
∴∠BAD=∠DAC.
∵∠FDA=∠BAD+∠B,∠FAD=∠DAC+∠CAF,
由(1)知∠FAD=∠FDA,
∴∠B=∠CAF.
∵∠B=50°,
∴∠CAF=50°.
27.
(1)结论:AE2+BF2=EF2 .
理由:如图1中,延长FD到M,使得DM=DF,连接AM,EM.
在△ADM和△BDF中,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2 ,
∴AE2+BF2=EF2 .
(2)如图2中,结论不变.AE2+BF2=EF2
理由:延长FD到M,使得DM=DF,连接AM,EM.
在△ADM和△BDF中,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=∠CAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2 ,
∴AE2+BF2=EF2 .
28.
(1)证明:在△ABC中,∵∠C=90°,∠B=30°,
∴∠CAB=60°,
又∵AD平分∠CAB,
∴∠DAB=∠DAC=∠CAB=30°,
∴∠DAB=∠B,
∴AD=DB.
(2)解:在△AEF中,∵∠AFE=90°,∠EAF=60°,
∴∠AEF=30°,
∴AE=AC-EC=6-x,AF=AE= (6 x),
在Rt△ABC中,∵∠B=30°,AC=6,
∴AB=12,
∴BF=AB-AF=12- (6 x)=9+x,
∴y=9+x,
答:y关于x的函数解析式是y=9+x(0<x<6).
(3)解:当∠DEF=90°时,∠CED=180°-∠AEF-∠FED=60°,
∴∠EDC=30°,ED=2x,
∵∠C=90°,∠DAC=30°,
∴∠ADC=60°,
∴∠EDA=60°-30°=30°=∠DAE,
∴ED=AE=6-x.
∴有2x=6-x,得x=2,
此时,y=9+×2=10,
答:BF的长为10.
