5.1.3 同位角、内错角、同旁内角 课件(共18张PPT)数学人教版七年级下册
文档属性
| 名称 | 5.1.3 同位角、内错角、同旁内角 课件(共18张PPT)数学人教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 648.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 18:29:34 | ||
图片预览

文档简介
(共18张PPT)
5.1 相交线
(第三课时)
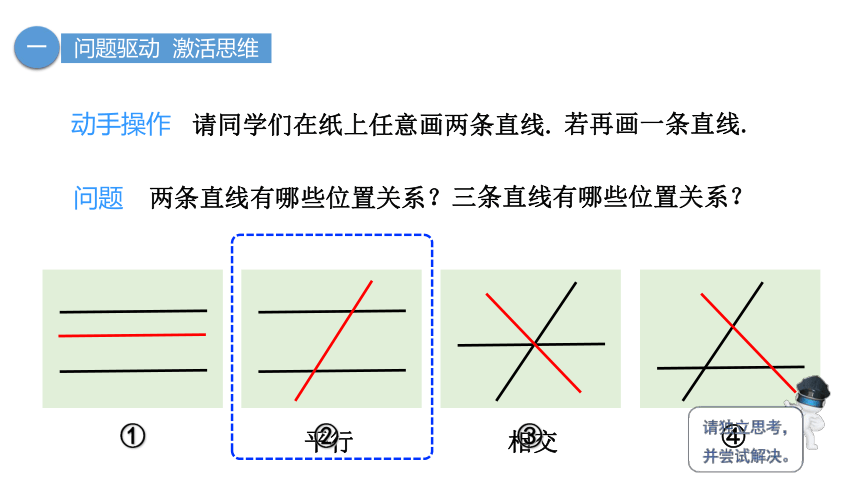
问题 两条直线有哪些位置关系?
请同学们在纸上任意画两条直线.
动手操作
问题驱动 激活思维
一
平行
相交
若再画一条直线.
三条直线有哪些位置关系?
①
②
③
④
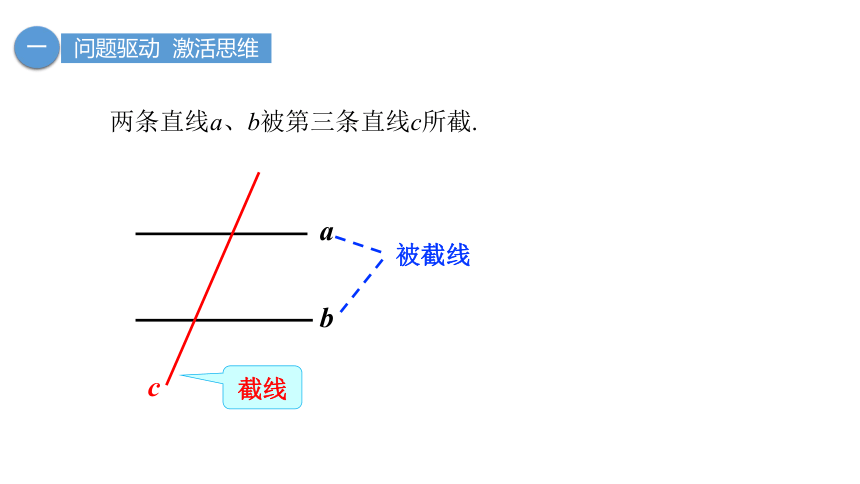
两条直线a、b被第三条直线c所截.
截线
被截线
a
b
c
问题驱动 激活思维
一
没有公共顶点的两个角,如图中的∠1和∠5,∠3和∠5,∠4和∠5又分别叫做什么角呢?
a
b
c
c
a
1
5
b
探究新知 建构思维
二
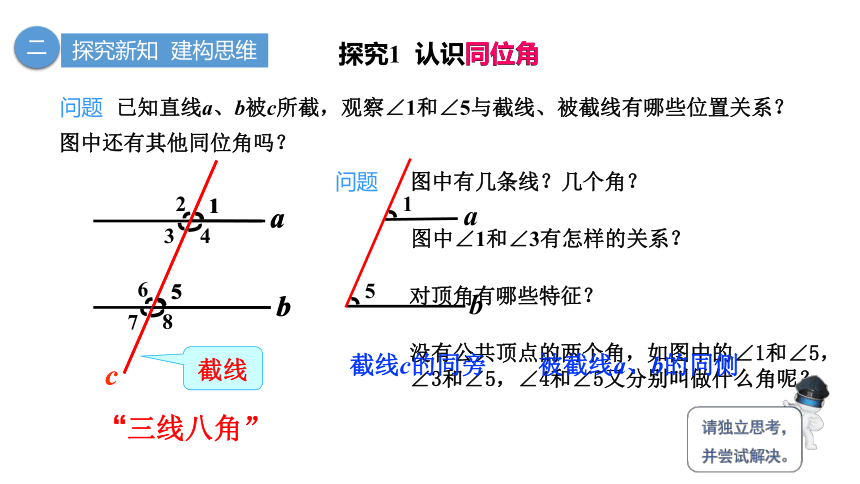
问题 已知直线a、b被c所截,观察∠1和∠5与截线、被截线有哪些位置关系?
截线c的同旁
a
1
5
b
被截线a、b的同侧
探究1 认识同位角
同位角
“三线八角”
截线
1
2
3
4
5
6
7
8
图中∠1和∠3有怎样的关系?
对顶角有哪些特征?
问题
图中有几条线?几个角?
图中还有其他同位角吗?
2
6
1
5
4
8
b
①
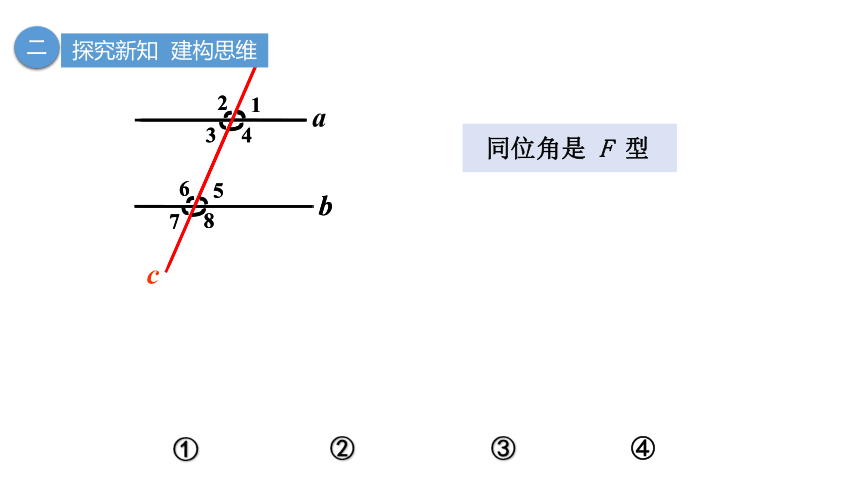
同位角是 F 型
②
③
④
3
7
a
b
c
1
2
3
4
5
6
7
8
探究新知 建构思维
二
6
探究新知 建构思维
二
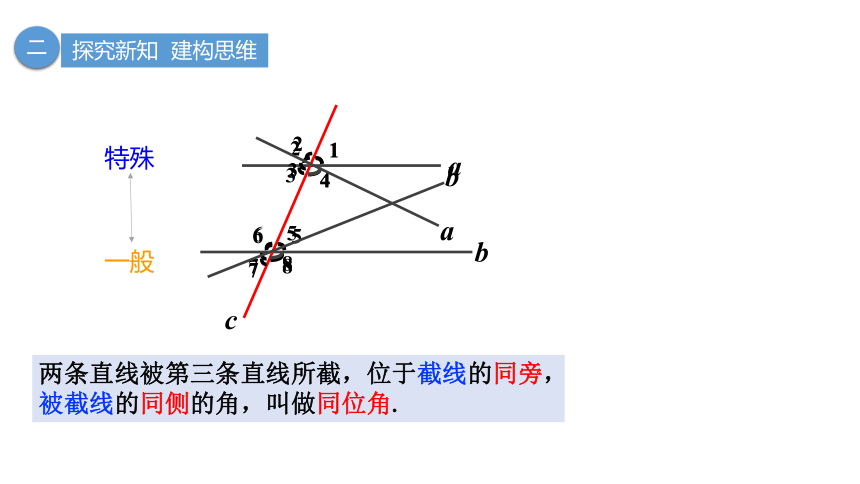
两条直线被第三条直线所截,位于截线的同旁,被截线的同侧的角,叫做同位角.
1
a
b
c
2
3
4
5
7
8
1
2
3
4
5
6
7
8
b
a
特殊
一般
探究新知 建构思维
二
1
2
( )
( )
1
2
( )
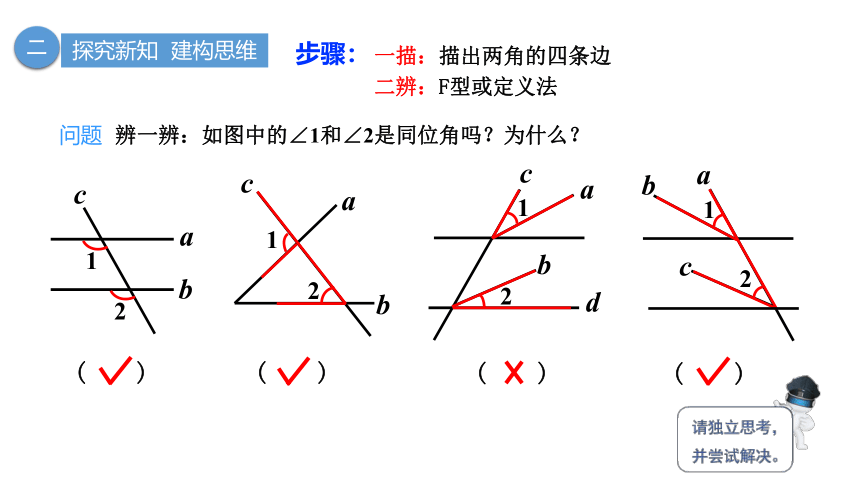
问题 辨一辨:如图中的∠1和∠2是同位角吗?为什么?
a
b
c
a
b
c
a
b
c
d
b
c
a
1
2
( )
1
2
一描:描出两角的四条边
二辨:F型或定义法
步骤:
探究新知 建构思维
二
自学要求:
1.结合课本第6页,第4自然段(如下图);
2.弄清两角与截线、被截线的位置关系;
3.同旁内角可以用哪个英文字母来概括?
4.内错角可以用哪个英文字母来概括?
B
D
F
1
2
3
4
5
6
7
8
A
C
E
探究新知 建构思维
二
c
a
5
b
4
c
问题 已知直线a、b被c所截,观察∠4和∠5与截线、被截线有哪些位置关系?
截线c的同旁
被截线a、b之间
探究2 认识同旁内角
两条直线被第三条直线所截,位于截线的同旁,被截线之间的角,叫做同旁内角.
a
5
b
4
a
b
c
1
2
3
4
5
6
7
8
探究新知 建构思维
二
c
5
4
3
6
a
b
c
1
2
3
4
5
6
7
8
同旁内角是 C 型
a
b
c
1
2
3
4
5
6
7
8
探究新知 建构思维
二
问题 已知直线a、b被c所截,观察∠3和∠5与截线、被截线有哪些位置关系?
被截线a、b之间
探究3 认识内错角
两条直线被第三条直线所截,位于截线的两侧,被截线之间的角,叫做内错角.
3
5
3
5
截线c的两侧
探究新知 建构思维
二
c
4
6
3
5
a
b
c
1
2
3
4
5
6
7
8
内错角是 Z 型
截线 被截线 结构特征
同位角
同旁内角
内错角
之间
之间
同侧
同旁
两侧
同旁
F型
Z型
C型
探究新知 建构思维
二
知识梳理
如图,直线DE,BC被直线AB所截.
例
(1)∠1和∠2是内错角,
∠1和∠3是同旁内角,
∠1和∠4是同位角.
解
例
题
演
练
应用迁移 拓展思维
三
A
2
C
B
4
3
1
D
E
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
(2)因为∠1=∠4,
由对顶角相等,得∠4=∠2,
所以∠1=∠2.
由邻补角定义,得∠3+∠4=180°,
因为∠1=∠4,
所以∠1+∠3=180°,
即∠1和∠3互补.
已知截线,直接辨认
(1)∠1和∠2,∠1和∠3,∠1和∠4各是什么位置关系的角?
图1
变式1 如图1.
例
题
演
练
应用迁移 拓展思维
三
∠1和∠2是 与 被 所截构成的 角.
∠3和∠4是 与 被 所截构成的 角.
∠1和∠2是 与 被 所截构成的 角.
∠3和∠4是 与 被 所截构成的 角.
AB CD BD 内错
AD BC BD 内错
AB CD BC 同旁内
AD BC AB 同位
变式2 如图2.
图2
截线怎么找?
两角顶点的连线.
两角的公共边.
截线未知
先找后辨
.
.
如图,请找出∠A的同位角
变式3
∠A和∠2是内错角.
∠A和∠1是同旁内角.
当AC是截线时,∠A和∠6是同位角.
∠A和∠8是内错角.
∠A和∠5是同旁内角.
解
当AB是截线时,∠A和∠4是同位角.
应用迁移 拓展思维
三
思考 截线是哪条直线?
生
长
拓
学
A
2
8
7
6
5
4
3
1
B
C
找准截线是关键!
答:∠A的同位角是∠4和∠6.
∠A的内错角是∠2和∠8.
∠A的同旁内角是∠1和∠5.
分类思想
、内错角和同旁内角.
如图,请找出所有的同位角、内错角和同旁内角.
变式4
解
应用迁移 拓展思维
三
思考 截线可能是哪几条直线?
生
长
拓
学
截线 同位角 内错角 同旁内角
AE
AB
CD
CF
∠A和∠1 ∠A和∠2
∠A和∠4 ∠A和∠3
∠C和∠1 ∠C和∠2
∠C和∠4 ∠C和∠3
知识
方法
生长
梳理小结 深化思维
四
找截线的方法:
①两角顶点的连线.
②两角的公共边.
辨认的步骤:
①描:描出两个角的四条边.
②辨:定义法或字母结构法.
思想
特殊
到一般
分类思想
方程思想
已知截线
直接辨认
截线未知
先找后辨
...
抽象
5.1 相交线
(第三课时)
问题 两条直线有哪些位置关系?
请同学们在纸上任意画两条直线.
动手操作
问题驱动 激活思维
一
平行
相交
若再画一条直线.
三条直线有哪些位置关系?
①
②
③
④
两条直线a、b被第三条直线c所截.
截线
被截线
a
b
c
问题驱动 激活思维
一
没有公共顶点的两个角,如图中的∠1和∠5,∠3和∠5,∠4和∠5又分别叫做什么角呢?
a
b
c
c
a
1
5
b
探究新知 建构思维
二
问题 已知直线a、b被c所截,观察∠1和∠5与截线、被截线有哪些位置关系?
截线c的同旁
a
1
5
b
被截线a、b的同侧
探究1 认识同位角
同位角
“三线八角”
截线
1
2
3
4
5
6
7
8
图中∠1和∠3有怎样的关系?
对顶角有哪些特征?
问题
图中有几条线?几个角?
图中还有其他同位角吗?
2
6
1
5
4
8
b
①
同位角是 F 型
②
③
④
3
7
a
b
c
1
2
3
4
5
6
7
8
探究新知 建构思维
二
6
探究新知 建构思维
二
两条直线被第三条直线所截,位于截线的同旁,被截线的同侧的角,叫做同位角.
1
a
b
c
2
3
4
5
7
8
1
2
3
4
5
6
7
8
b
a
特殊
一般
探究新知 建构思维
二
1
2
( )
( )
1
2
( )
问题 辨一辨:如图中的∠1和∠2是同位角吗?为什么?
a
b
c
a
b
c
a
b
c
d
b
c
a
1
2
( )
1
2
一描:描出两角的四条边
二辨:F型或定义法
步骤:
探究新知 建构思维
二
自学要求:
1.结合课本第6页,第4自然段(如下图);
2.弄清两角与截线、被截线的位置关系;
3.同旁内角可以用哪个英文字母来概括?
4.内错角可以用哪个英文字母来概括?
B
D
F
1
2
3
4
5
6
7
8
A
C
E
探究新知 建构思维
二
c
a
5
b
4
c
问题 已知直线a、b被c所截,观察∠4和∠5与截线、被截线有哪些位置关系?
截线c的同旁
被截线a、b之间
探究2 认识同旁内角
两条直线被第三条直线所截,位于截线的同旁,被截线之间的角,叫做同旁内角.
a
5
b
4
a
b
c
1
2
3
4
5
6
7
8
探究新知 建构思维
二
c
5
4
3
6
a
b
c
1
2
3
4
5
6
7
8
同旁内角是 C 型
a
b
c
1
2
3
4
5
6
7
8
探究新知 建构思维
二
问题 已知直线a、b被c所截,观察∠3和∠5与截线、被截线有哪些位置关系?
被截线a、b之间
探究3 认识内错角
两条直线被第三条直线所截,位于截线的两侧,被截线之间的角,叫做内错角.
3
5
3
5
截线c的两侧
探究新知 建构思维
二
c
4
6
3
5
a
b
c
1
2
3
4
5
6
7
8
内错角是 Z 型
截线 被截线 结构特征
同位角
同旁内角
内错角
之间
之间
同侧
同旁
两侧
同旁
F型
Z型
C型
探究新知 建构思维
二
知识梳理
如图,直线DE,BC被直线AB所截.
例
(1)∠1和∠2是内错角,
∠1和∠3是同旁内角,
∠1和∠4是同位角.
解
例
题
演
练
应用迁移 拓展思维
三
A
2
C
B
4
3
1
D
E
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
(2)因为∠1=∠4,
由对顶角相等,得∠4=∠2,
所以∠1=∠2.
由邻补角定义,得∠3+∠4=180°,
因为∠1=∠4,
所以∠1+∠3=180°,
即∠1和∠3互补.
已知截线,直接辨认
(1)∠1和∠2,∠1和∠3,∠1和∠4各是什么位置关系的角?
图1
变式1 如图1.
例
题
演
练
应用迁移 拓展思维
三
∠1和∠2是 与 被 所截构成的 角.
∠3和∠4是 与 被 所截构成的 角.
∠1和∠2是 与 被 所截构成的 角.
∠3和∠4是 与 被 所截构成的 角.
AB CD BD 内错
AD BC BD 内错
AB CD BC 同旁内
AD BC AB 同位
变式2 如图2.
图2
截线怎么找?
两角顶点的连线.
两角的公共边.
截线未知
先找后辨
.
.
如图,请找出∠A的同位角
变式3
∠A和∠2是内错角.
∠A和∠1是同旁内角.
当AC是截线时,∠A和∠6是同位角.
∠A和∠8是内错角.
∠A和∠5是同旁内角.
解
当AB是截线时,∠A和∠4是同位角.
应用迁移 拓展思维
三
思考 截线是哪条直线?
生
长
拓
学
A
2
8
7
6
5
4
3
1
B
C
找准截线是关键!
答:∠A的同位角是∠4和∠6.
∠A的内错角是∠2和∠8.
∠A的同旁内角是∠1和∠5.
分类思想
、内错角和同旁内角.
如图,请找出所有的同位角、内错角和同旁内角.
变式4
解
应用迁移 拓展思维
三
思考 截线可能是哪几条直线?
生
长
拓
学
截线 同位角 内错角 同旁内角
AE
AB
CD
CF
∠A和∠1 ∠A和∠2
∠A和∠4 ∠A和∠3
∠C和∠1 ∠C和∠2
∠C和∠4 ∠C和∠3
知识
方法
生长
梳理小结 深化思维
四
找截线的方法:
①两角顶点的连线.
②两角的公共边.
辨认的步骤:
①描:描出两个角的四条边.
②辨:定义法或字母结构法.
思想
特殊
到一般
分类思想
方程思想
已知截线
直接辨认
截线未知
先找后辨
...
抽象
