7.1.1 有序数对 课件(共22张PPT)数学人教版七年级下册
文档属性
| 名称 | 7.1.1 有序数对 课件(共22张PPT)数学人教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
7.1.1有序数对
年 级:七年级
学 科:初中数学(人教版)
问题1:同学们都有去影剧院看电影的经历,你怎么找到自己的座位?
答:根据入场卷上的“排数”和“号数”就可以准确地“对号入座”.
追问:确定一个座位一般需要几个数据?
答:两个数据,分别为“排数”和“号数”.
情境引入
情境引入
问题2:你若发现一本书某页有一处印刷错误,怎样告诉其他同学这一处的位置?
答:说明该页上“第几行”和“第几个字”,就可以找到错误的位置.
追问:确定一个字的位置一般需要几个数据?
答:两个数据,分别为“行数”和“个数”.
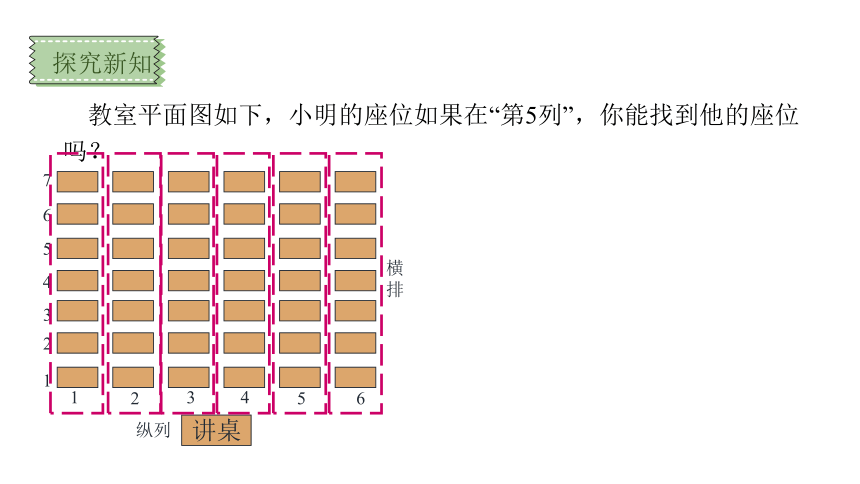
教室平面图如下,小明的座位如果在“第5列”,你能找到他的座位吗?
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
探究新知
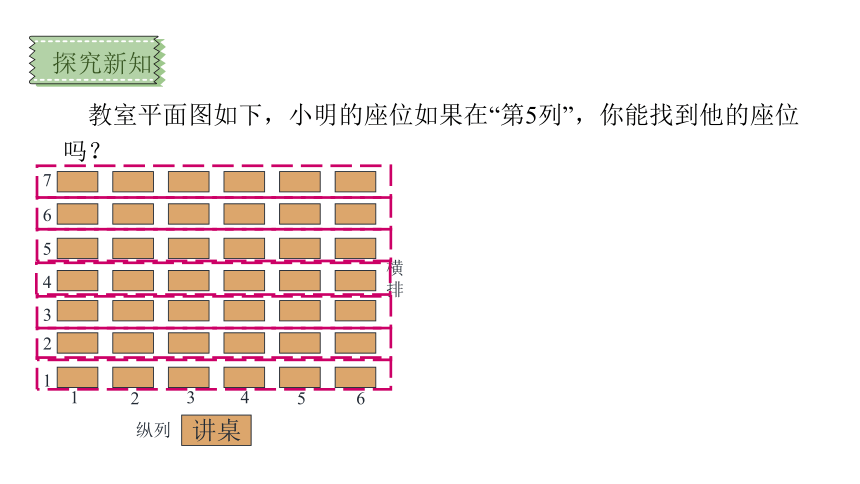
教室平面图如下,小明的座位如果在“第5列”,你能找到他的座位吗?
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
探究新知
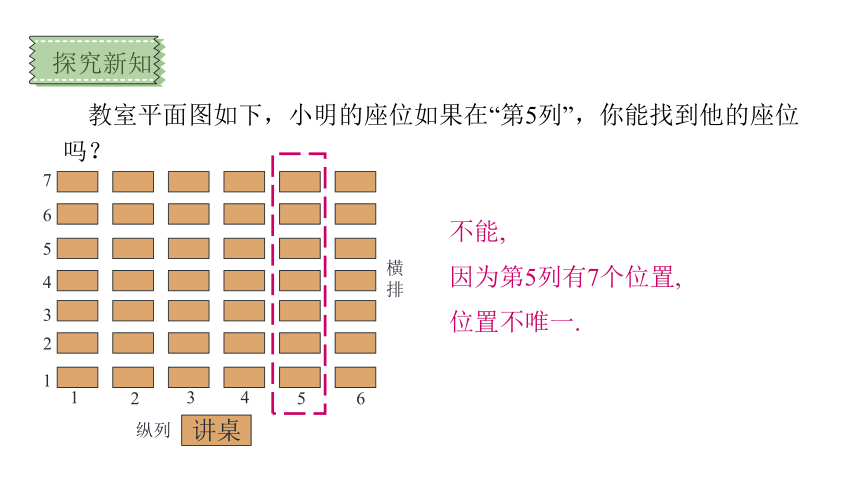
教室平面图如下,小明的座位如果在“第5列”,你能找到他的座位吗?
不能,
因为第5列有7个位置,
位置不唯一.
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
探究新知
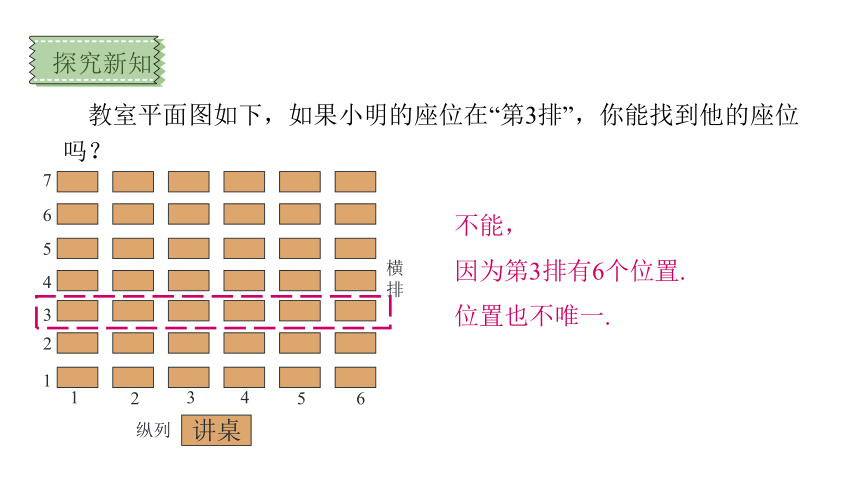
教室平面图如下,如果小明的座位在“第3排”,你能找到他的座位吗?
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
探究新知
不能,
因为第3排有6个位置.
位置也不唯一.
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
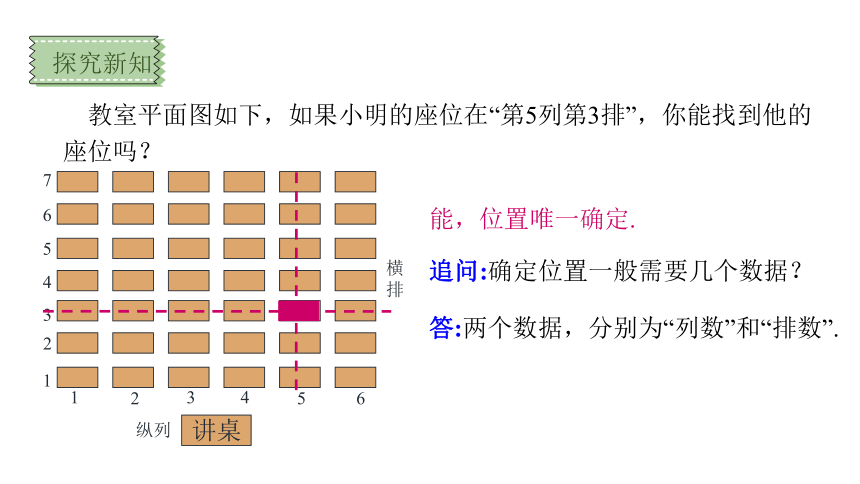
教室平面图如下,如果小明的座位在“第5列第3排”,你能找到他的座位吗?
探究新知
能,位置唯一确定.
追问:确定位置一般需要几个数据?
答:两个数据,分别为“列数”和“排数”.
探究新知
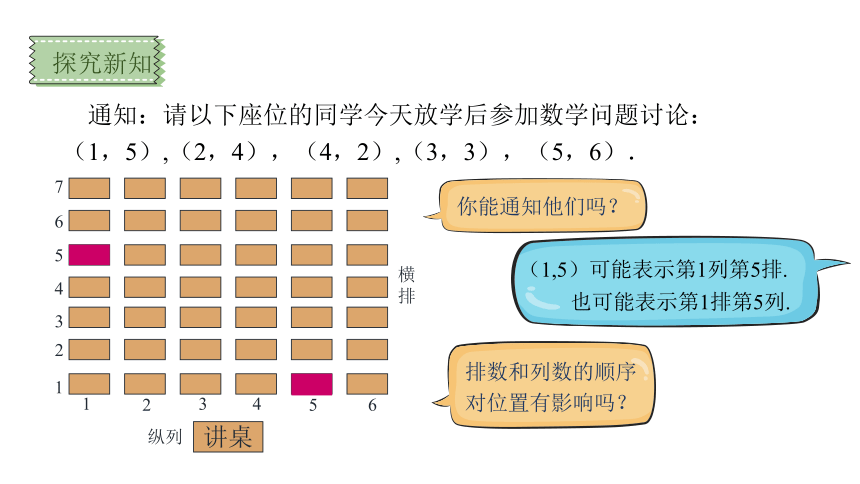
通知:请以下座位的同学今天放学后参加数学问题讨论:
(1,5),(2,4),(4,2),(3,3),(5,6).
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
你能通知他们吗?
(1,5)可能表示第1列第5排.
也可能表示第1排第5列.
排数和列数的顺序对位置有影响吗?
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
(1,5)
(2,4)
(4,2)
(3,3)
(5,6)
探究新知
通知:请以下座位的同学今天放学后参加数学问题讨论:
(1,5),(2,4),(4,2),(3,3),(5,6).
我们约定:
“列数在前,排数在后”.
你能通知他们吗?
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
第3列,第5排
第5列,第3排
探究新知
通知:请以下座位的同学今天放学后参加数学问题讨论:
(1,5),(2,4),(4,2),(3,3),(5,6).
第3列第5排怎么表示?
第5列第3排怎么表示?
我们约定:
“列数在前,排数在后”.
(3,5)
(5,3)
探究新知
通知:请以下座位的同学今天放学后参加数学问题讨论:
(1,5),(2,4),(4,2),(3,3),(5,6).
(3,5),(5,3),他们在同一位置吗?
我们约定:
“列数在前,排数在后”.
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
第3列,第5排
第5列,第3排
通过这样含有两个数的表达方式来表示一个确定的位置,其中两个数各自表示不同的含义,我们把这种有顺序的两个数a与b组成的数对,叫做有序数对.记作(a,b).
像上面“7排9号”
“第5列第3排”
(7,9)
(5,3)
形成概念
“第3列第5排”
(3,5)
特别地,(a,b)与(b,a)(a≠b)表示两个不同的位置.
生活中有很多利用有序数对表示位置的情况,如人们常用经纬度来表示地球上的地点等,只要指明一点的经度和维度,就可以确定地球上这一点的位置.
举例:经纬度表示位置
例如:北京在东经116.4°,北纬39.9°.
地球仪出处:人教版数学七下,人民教育出版社,2012年10月第1版,第72页
1 2 3 4 5 6 7 8 9
10
9
8
7
6
5
4
3
2
1
举例:棋盘
棋子在棋盘的位置
1.以下是某班几位同学写出来的几个有序数对,谁写对了?
A (5、9)
B (x,y)
E (b,9)
C 4,6
D (a b)
×
√
×
×
√
辨一辩
2.下列数据中不能确定物体位置的是( )
A.1单元201号
B.南偏西60°
C.学院路11号
D.东经105°,北纬40°
B
选一选
3.如果电影票上的“4排3座”记作(4,3),
那么6排8座可记作 ,
(8,6)表示 排 座.
6
8
(6,8)
填一填
4.如图,棋子B在(2,1)处,用有序数对表示出图中另外六枚棋子的位置.
A(0,0)
用有序数对表示点的位置
C(3,3)
D(1,2)
E(4,1)
F(2,4)
G(5,4)
列数在前,行数在后
A.(1,3)
B.(3,4)
C.(4,2)
D.(2,4)
5.如图是一个教室平面示意图,我们把小刚的座位“第1列第3排”记为(1,3).若小丽的座位为(3,2),以下四个座位中,与小丽相邻且能比较方便地讨论交流的同学的座位是( )
C
思考题
6.如图,甲处表示2街与5巷的十字路口,乙处表示5街与2巷的十字路口,
如果用(2,5)表示甲处的位置,那么“(2,5)→(3,5) →(4,5) →(5,5)→(5,4) →(5,3) →(5,2)”表示从甲处到乙处的一种路线,请你用这种形式写出几种从甲处到乙处的路线.
1街
2街
3街
4街
5街
6街
1巷
2巷
3巷
4巷
5巷
6巷
甲
乙
(2,5)
(5,2)
(3,5)
(4,5)
(5,5)
(5,4)
(5,3)
解: (2,5)→(2,4) →(2,3)→(2,2) →(3,2) →(4,2)→(5,2).
思考题
(2,4)
(2,3)
(2,2)
(3,2)
(4,2)
有序数对
点的位置
注意
有顺序的两个数a与b组成的数对.
定义
(a,b)与(b,a)(a≠b)表示两个不同的位置.
记作(a,b),两个数逗号隔开,加上括号.
课堂小结
表示方法
7.1.1有序数对
年 级:七年级
学 科:初中数学(人教版)
问题1:同学们都有去影剧院看电影的经历,你怎么找到自己的座位?
答:根据入场卷上的“排数”和“号数”就可以准确地“对号入座”.
追问:确定一个座位一般需要几个数据?
答:两个数据,分别为“排数”和“号数”.
情境引入
情境引入
问题2:你若发现一本书某页有一处印刷错误,怎样告诉其他同学这一处的位置?
答:说明该页上“第几行”和“第几个字”,就可以找到错误的位置.
追问:确定一个字的位置一般需要几个数据?
答:两个数据,分别为“行数”和“个数”.
教室平面图如下,小明的座位如果在“第5列”,你能找到他的座位吗?
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
探究新知
教室平面图如下,小明的座位如果在“第5列”,你能找到他的座位吗?
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
探究新知
教室平面图如下,小明的座位如果在“第5列”,你能找到他的座位吗?
不能,
因为第5列有7个位置,
位置不唯一.
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
探究新知
教室平面图如下,如果小明的座位在“第3排”,你能找到他的座位吗?
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
探究新知
不能,
因为第3排有6个位置.
位置也不唯一.
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
教室平面图如下,如果小明的座位在“第5列第3排”,你能找到他的座位吗?
探究新知
能,位置唯一确定.
追问:确定位置一般需要几个数据?
答:两个数据,分别为“列数”和“排数”.
探究新知
通知:请以下座位的同学今天放学后参加数学问题讨论:
(1,5),(2,4),(4,2),(3,3),(5,6).
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
你能通知他们吗?
(1,5)可能表示第1列第5排.
也可能表示第1排第5列.
排数和列数的顺序对位置有影响吗?
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
(1,5)
(2,4)
(4,2)
(3,3)
(5,6)
探究新知
通知:请以下座位的同学今天放学后参加数学问题讨论:
(1,5),(2,4),(4,2),(3,3),(5,6).
我们约定:
“列数在前,排数在后”.
你能通知他们吗?
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
第3列,第5排
第5列,第3排
探究新知
通知:请以下座位的同学今天放学后参加数学问题讨论:
(1,5),(2,4),(4,2),(3,3),(5,6).
第3列第5排怎么表示?
第5列第3排怎么表示?
我们约定:
“列数在前,排数在后”.
(3,5)
(5,3)
探究新知
通知:请以下座位的同学今天放学后参加数学问题讨论:
(1,5),(2,4),(4,2),(3,3),(5,6).
(3,5),(5,3),他们在同一位置吗?
我们约定:
“列数在前,排数在后”.
1
讲桌
2
3
4
5
6
1
2
3
4
5
6
7
纵列
横
排
第3列,第5排
第5列,第3排
通过这样含有两个数的表达方式来表示一个确定的位置,其中两个数各自表示不同的含义,我们把这种有顺序的两个数a与b组成的数对,叫做有序数对.记作(a,b).
像上面“7排9号”
“第5列第3排”
(7,9)
(5,3)
形成概念
“第3列第5排”
(3,5)
特别地,(a,b)与(b,a)(a≠b)表示两个不同的位置.
生活中有很多利用有序数对表示位置的情况,如人们常用经纬度来表示地球上的地点等,只要指明一点的经度和维度,就可以确定地球上这一点的位置.
举例:经纬度表示位置
例如:北京在东经116.4°,北纬39.9°.
地球仪出处:人教版数学七下,人民教育出版社,2012年10月第1版,第72页
1 2 3 4 5 6 7 8 9
10
9
8
7
6
5
4
3
2
1
举例:棋盘
棋子在棋盘的位置
1.以下是某班几位同学写出来的几个有序数对,谁写对了?
A (5、9)
B (x,y)
E (b,9)
C 4,6
D (a b)
×
√
×
×
√
辨一辩
2.下列数据中不能确定物体位置的是( )
A.1单元201号
B.南偏西60°
C.学院路11号
D.东经105°,北纬40°
B
选一选
3.如果电影票上的“4排3座”记作(4,3),
那么6排8座可记作 ,
(8,6)表示 排 座.
6
8
(6,8)
填一填
4.如图,棋子B在(2,1)处,用有序数对表示出图中另外六枚棋子的位置.
A(0,0)
用有序数对表示点的位置
C(3,3)
D(1,2)
E(4,1)
F(2,4)
G(5,4)
列数在前,行数在后
A.(1,3)
B.(3,4)
C.(4,2)
D.(2,4)
5.如图是一个教室平面示意图,我们把小刚的座位“第1列第3排”记为(1,3).若小丽的座位为(3,2),以下四个座位中,与小丽相邻且能比较方便地讨论交流的同学的座位是( )
C
思考题
6.如图,甲处表示2街与5巷的十字路口,乙处表示5街与2巷的十字路口,
如果用(2,5)表示甲处的位置,那么“(2,5)→(3,5) →(4,5) →(5,5)→(5,4) →(5,3) →(5,2)”表示从甲处到乙处的一种路线,请你用这种形式写出几种从甲处到乙处的路线.
1街
2街
3街
4街
5街
6街
1巷
2巷
3巷
4巷
5巷
6巷
甲
乙
(2,5)
(5,2)
(3,5)
(4,5)
(5,5)
(5,4)
(5,3)
解: (2,5)→(2,4) →(2,3)→(2,2) →(3,2) →(4,2)→(5,2).
思考题
(2,4)
(2,3)
(2,2)
(3,2)
(4,2)
有序数对
点的位置
注意
有顺序的两个数a与b组成的数对.
定义
(a,b)与(b,a)(a≠b)表示两个不同的位置.
记作(a,b),两个数逗号隔开,加上括号.
课堂小结
表示方法
