8.3 实际问题与二元一次方程组 课件(共15张PPT)数学人教版七年级下册
文档属性
| 名称 | 8.3 实际问题与二元一次方程组 课件(共15张PPT)数学人教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 569.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
8.3实际问题与二元一次方程组
年 级:七年级
学 科:初中数学(人教版)
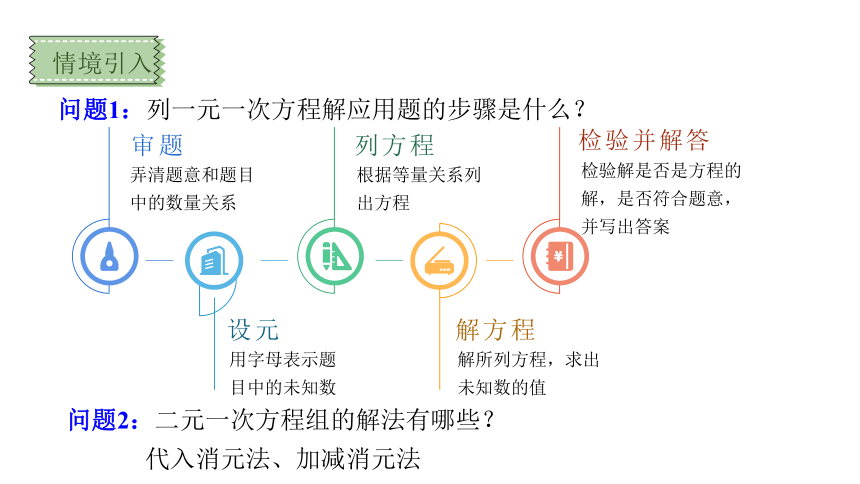
问题1:列一元一次方程解应用题的步骤是什么?
情境引入
解方程
解所列方程,求出未知数的值
设元
用字母表示题目中的未知数
审题
弄清题意和题目中的数量关系
列方程
根据等量关系列出方程
检验并解答
检验解是否是方程的解,是否符合题意,并写出答案
问题2:二元一次方程组的解法有哪些?
代入消元法、加减消元法
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验李大叔的估计吗?
探究1
问题1:你如何理解“通过计算检验他的估计”这句话?
问题2:题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天约需多少饲料,每头小牛1天约需多少饲料.
设未知数:设每头大牛和每头小牛平均1天各需用饲料为x kg和y kg
探究1
问题3:你能在问题中把表示等量关系的语句找出来,并用等式进行表示吗?
30头大牛1天食量+15头小牛1天食量=679kg饲料总量
42头大牛1天食量+20头小牛1天食量=940kg饲料总量
问题4:你能依据上面的等量关系列出方程组吗?
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验李大叔的估计吗?
探究1
解:设每头大牛1天约用饲料x kg,每头小牛1天约用饲料y kg,
则
+ = 675,
+ = 940.
30x
15y
42x
20y
所以,每头大牛1天约需饲料20kg,每头小牛1天约需饲料5kg.因此,饲养员李大叔对大牛的食量估计正确,对小牛的食量估计错误.
解方程组得
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验李大叔的估计吗?
D
A
200m
100m
B
C
F
E
甲种作物
乙种作物
x
y
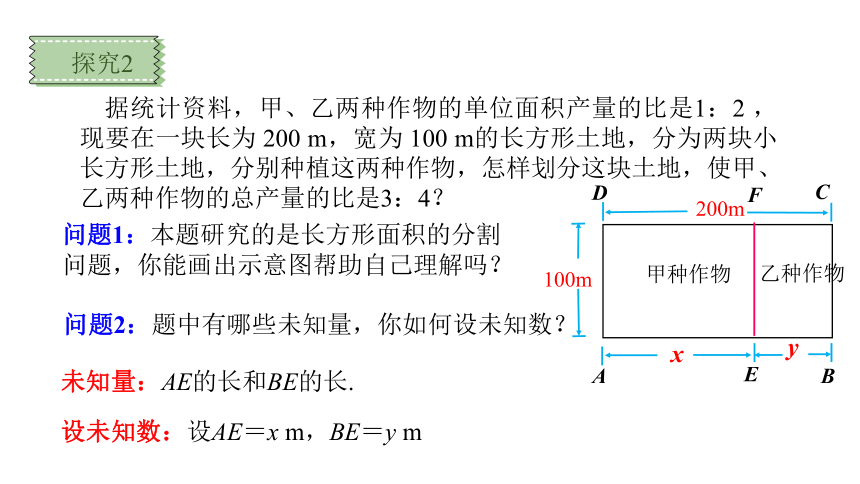
探究2
问题1:本题研究的是长方形面积的分割问题,你能画出示意图帮助自己理解吗?
问题2:题中有哪些未知量,你如何设未知数?
未知量:AE的长和BE的长.
设未知数:设AE=x m,BE=y m
据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要在一块长为 200 m,宽为 100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物,怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
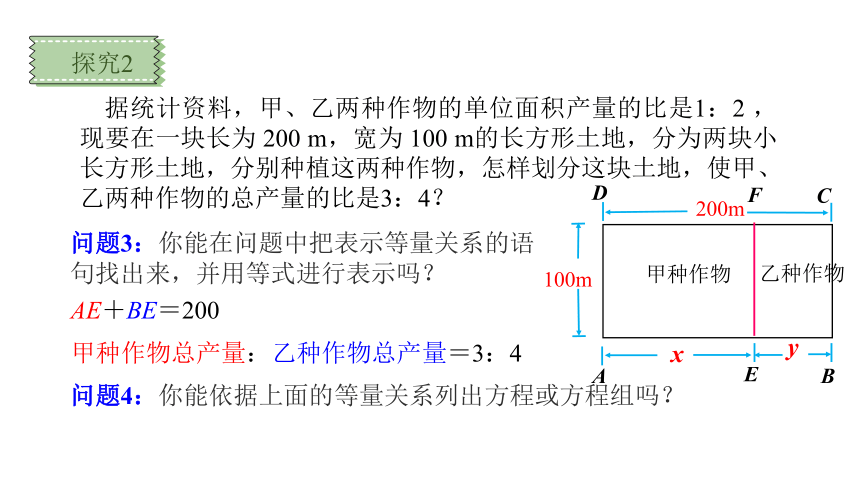
探究2
据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要在一块长为 200 m,宽为 100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物,怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
问题3:你能在问题中把表示等量关系的语句找出来,并用等式进行表示吗?
AE+BE=200
甲种作物总产量:乙种作物总产量=3:4
问题4:你能依据上面的等量关系列出方程或方程组吗?
x
y
D
F
E
A
C
200m
100m
甲种作物
乙种作物
B
探究2
据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要在一块长为 200 m,宽为 100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物,怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
问题5:还有其他设计方案吗?
答:过长方形土地的长边上离一端80米处,作这条边的垂线,把这块地分为两个长方形土地,较大一块地种甲作物,较小一块地种乙作物.
x
y
D
F
E
A
C
200m
100m
甲种作物
乙种作物
B
则
x+y=200
解方程组得
x=120
y=80
解:
在AB上取点E,作EF⊥AB,交CD于点F
设AE=x m,BE=y m
甲种作物的单位面积产量是a
乙种作物的单位面积产量是2a
x+y=100
解:在AD上取点E,作EF⊥AD,交BC于点F
设DE=x m,AE=y m
x=60
y=40
解方程组得
则
A
D
C
B
E
x
y
F
乙种作物
甲种作物
200m
100m
答:将这块土地分为长200m,宽60m和长200m,宽40m的
两个小长方形分别种植甲、乙两种作物.
探究2
据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要在一块长为 200 m,宽为 100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物,怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
探究3
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
铁路
铁路
公路
公路
长青化工厂
A
问题1:要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
销售款-(原料费+运输费)
产品数量
原料数量
因此,设制成 x t 产品, 购买 y t 原料
探究3
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
问题2:本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.
产品 x 吨 原料 y 吨 合计
公路运费(元)
铁路运费(元)
1.5
15000
97200
铁路
铁路
公路
公路
长青化工厂
A
探究3
公路运价为1.5元/(t·km)
铁路运价为1.2元/(t·km)
×y
×10
1.2
×y
×120
1.2
×x
×110
1.5
×x
×20
问题3:从上表中你发现等量关系了吗?如何列方程组?
探究3
产品 x 吨 原料 y 吨 合计
公路运费(元)
铁路运费(元)
1.5
15000
97200
×y
×10
1.2
×y
×120
1.2
×x
×110
1.5
×x
×20
1.5×20x+1.5×10y=15000
1.2×110x+1.2×120y=97200
解:设制成 x t产品,购买 y t原料.根据题意,得
销售款为:
8000×300=2400000(元)
原料费为:
1000×400=400000(元)
运输费为:
15000+97200=112200(元)
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元.
解方程组得
探究3
1.5×20x+1.5×10y=15000
1.2×110x+1.2×120y=97200
这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.
课堂小结
解方程组
解所列方程组,求出未知数的值
设元
用字母表示题目中的未知数
审题
弄清题意和题目中的数量关系
列方程组
根据等量关系列出方程组
检验并解答
检验解是否是方程组的解,是否符合题意,并写出答案
列二元一次方程组解应用题的步骤:
8.3实际问题与二元一次方程组
年 级:七年级
学 科:初中数学(人教版)
问题1:列一元一次方程解应用题的步骤是什么?
情境引入
解方程
解所列方程,求出未知数的值
设元
用字母表示题目中的未知数
审题
弄清题意和题目中的数量关系
列方程
根据等量关系列出方程
检验并解答
检验解是否是方程的解,是否符合题意,并写出答案
问题2:二元一次方程组的解法有哪些?
代入消元法、加减消元法
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验李大叔的估计吗?
探究1
问题1:你如何理解“通过计算检验他的估计”这句话?
问题2:题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天约需多少饲料,每头小牛1天约需多少饲料.
设未知数:设每头大牛和每头小牛平均1天各需用饲料为x kg和y kg
探究1
问题3:你能在问题中把表示等量关系的语句找出来,并用等式进行表示吗?
30头大牛1天食量+15头小牛1天食量=679kg饲料总量
42头大牛1天食量+20头小牛1天食量=940kg饲料总量
问题4:你能依据上面的等量关系列出方程组吗?
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验李大叔的估计吗?
探究1
解:设每头大牛1天约用饲料x kg,每头小牛1天约用饲料y kg,
则
+ = 675,
+ = 940.
30x
15y
42x
20y
所以,每头大牛1天约需饲料20kg,每头小牛1天约需饲料5kg.因此,饲养员李大叔对大牛的食量估计正确,对小牛的食量估计错误.
解方程组得
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验李大叔的估计吗?
D
A
200m
100m
B
C
F
E
甲种作物
乙种作物
x
y
探究2
问题1:本题研究的是长方形面积的分割问题,你能画出示意图帮助自己理解吗?
问题2:题中有哪些未知量,你如何设未知数?
未知量:AE的长和BE的长.
设未知数:设AE=x m,BE=y m
据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要在一块长为 200 m,宽为 100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物,怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
探究2
据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要在一块长为 200 m,宽为 100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物,怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
问题3:你能在问题中把表示等量关系的语句找出来,并用等式进行表示吗?
AE+BE=200
甲种作物总产量:乙种作物总产量=3:4
问题4:你能依据上面的等量关系列出方程或方程组吗?
x
y
D
F
E
A
C
200m
100m
甲种作物
乙种作物
B
探究2
据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要在一块长为 200 m,宽为 100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物,怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
问题5:还有其他设计方案吗?
答:过长方形土地的长边上离一端80米处,作这条边的垂线,把这块地分为两个长方形土地,较大一块地种甲作物,较小一块地种乙作物.
x
y
D
F
E
A
C
200m
100m
甲种作物
乙种作物
B
则
x+y=200
解方程组得
x=120
y=80
解:
在AB上取点E,作EF⊥AB,交CD于点F
设AE=x m,BE=y m
甲种作物的单位面积产量是a
乙种作物的单位面积产量是2a
x+y=100
解:在AD上取点E,作EF⊥AD,交BC于点F
设DE=x m,AE=y m
x=60
y=40
解方程组得
则
A
D
C
B
E
x
y
F
乙种作物
甲种作物
200m
100m
答:将这块土地分为长200m,宽60m和长200m,宽40m的
两个小长方形分别种植甲、乙两种作物.
探究2
据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要在一块长为 200 m,宽为 100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物,怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
探究3
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
铁路
铁路
公路
公路
长青化工厂
A
问题1:要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
销售款-(原料费+运输费)
产品数量
原料数量
因此,设制成 x t 产品, 购买 y t 原料
探究3
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
问题2:本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.
产品 x 吨 原料 y 吨 合计
公路运费(元)
铁路运费(元)
1.5
15000
97200
铁路
铁路
公路
公路
长青化工厂
A
探究3
公路运价为1.5元/(t·km)
铁路运价为1.2元/(t·km)
×y
×10
1.2
×y
×120
1.2
×x
×110
1.5
×x
×20
问题3:从上表中你发现等量关系了吗?如何列方程组?
探究3
产品 x 吨 原料 y 吨 合计
公路运费(元)
铁路运费(元)
1.5
15000
97200
×y
×10
1.2
×y
×120
1.2
×x
×110
1.5
×x
×20
1.5×20x+1.5×10y=15000
1.2×110x+1.2×120y=97200
解:设制成 x t产品,购买 y t原料.根据题意,得
销售款为:
8000×300=2400000(元)
原料费为:
1000×400=400000(元)
运输费为:
15000+97200=112200(元)
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元.
解方程组得
探究3
1.5×20x+1.5×10y=15000
1.2×110x+1.2×120y=97200
这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.
课堂小结
解方程组
解所列方程组,求出未知数的值
设元
用字母表示题目中的未知数
审题
弄清题意和题目中的数量关系
列方程组
根据等量关系列出方程组
检验并解答
检验解是否是方程组的解,是否符合题意,并写出答案
列二元一次方程组解应用题的步骤:
