初中数学人教版七年级下册 第六章 实数 小结课件(17张PPT)
文档属性
| 名称 | 初中数学人教版七年级下册 第六章 实数 小结课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 356.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
第六章 实数的复习
问题一 什么是开方运算?
问题二 怎么进行开方运算?
问题驱动 激活思维
一
中心问题:
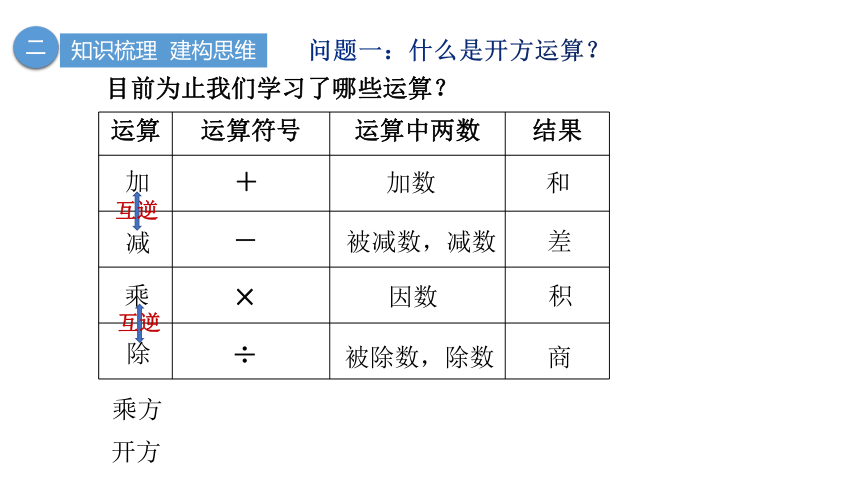
运算 运算符号 运算中两数 结果
+
-
×
加
减
除
乘
加数
和
被减数,减数
因数
差
积
被除数,除数
商
互逆
互逆
目前为止我们学习了哪些运算?
乘方
开方
问题一:什么是开方运算?
知识梳理 建构思维
二
乘方 开方 运算 运算符号 运算中两数 结果 运算 运算 符号 运算中两数 结果
底数,指数
底数,指数
二次幂
三次幂
(已知底数和指数求幂)
问题一:什么是开方运算?
平方
立方
开平方
被开方数(a)
根指数(2)
平方根
(二次方根)
=a
x=
开立方
被开方数(a)
根指数(3)
立方根
(三次方根)
(已知幂和指数求底数)
开n次方运算:求一个数的n次方根的运算
互逆
知识梳理 建构思维
二
被开方数 平方根 算术平方根 立方根
问题二:怎么进行开方运算?
64
-27
0
没有
没有
完成下表:
4
0
0
0
±8
8
-3
1.任何数都有平方根,立方根吗?有几个?它们之间有什么关系?
1.心算
定义
问题
知识梳理 建构思维
二
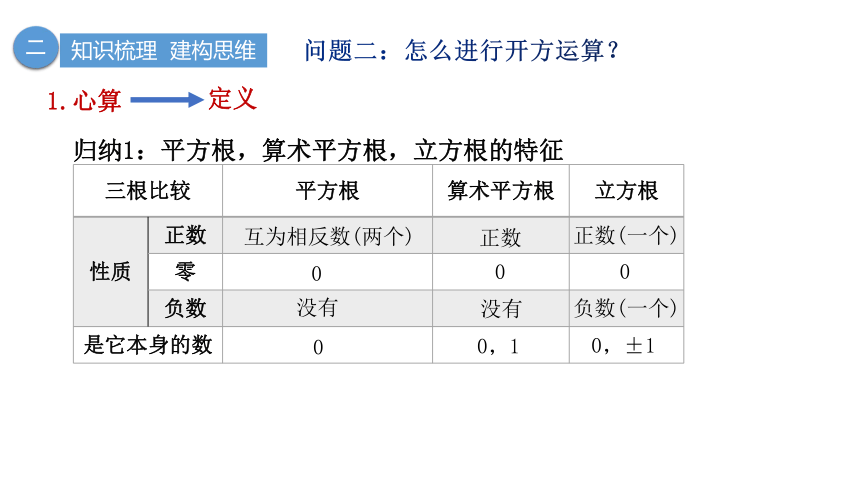
三根比较 平方根 算术平方根 立方根
性质 正数
零
负数
是它本身的数
归纳1:平方根,算术平方根,立方根的特征
1.心算
定义
互为相反数(两个)
正数
正数(一个)
0
0
0
没有
没有
负数(一个)
0
0,1
0,±1
问题二:怎么进行开方运算?
知识梳理 建构思维
二
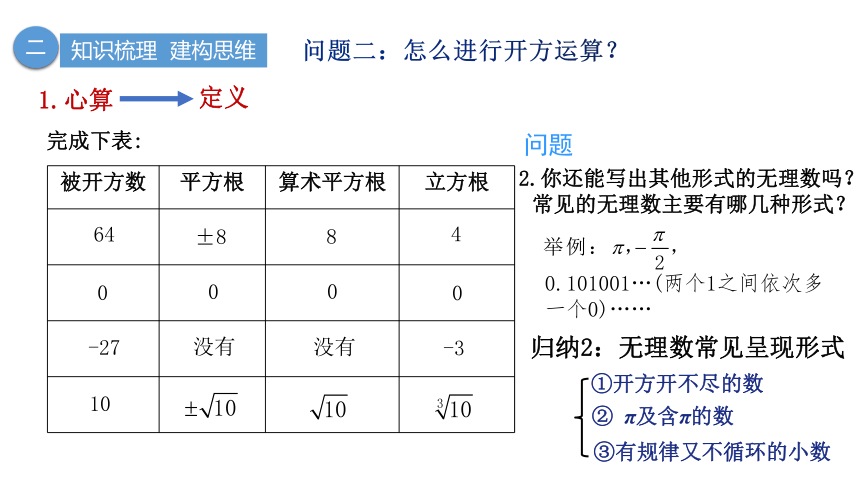
被开方数 平方根 算术平方根 立方根
2.你还能写出其他形式的无理数吗?
常见的无理数主要有哪几种形式?
64
-27
10
0
没有
没有
完成下表:
4
0
0
0
±8
8
-3
1.心算
定义
0.101001…(两个1之间依次多一个0)……)
归纳2:无理数常见呈现形式
③有规律又不循环的小数
①开方开不尽的数
② π及含π的数
问题二:怎么进行开方运算?
问题
知识梳理 建构思维
二
归纳3:数系的发展与实数的分类
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
正无理数
负无理数
有限小数及无限循环小数
无限不循环小数
问题二:怎么进行开方运算?
知识梳理 建构思维
二
,
属于有理数的有 ;
属于无理数的有 ;
属于负实数的有 ;
属于分数的有 .
问题二:怎么进行开方运算?
,0.262262226……
对实数进行分类时能化简的应先化简再判断;
是无理数不属于分数.
温馨提示:
归纳3:数系的发展与实数的分类
知识梳理 建构思维
二
问题
0.262262226……(两个6之间依次多一个2)中,)
被开方数 平方根 算术平方根 立方根
64
-27
10
0
没有
没有
完成下表:
4
0
0
0
±8
8
-3
问题二:怎么进行开方运算?
问题
3. 大概有多大呢?
2.估算
应用迁移 拓展思维
三
(2) 的整数部分是 ,小数部分是 .
2.估算
逼近法
问题
2
问题二:怎么进行开方运算?
(1) 界于哪两个相邻的整数之间?
可见 的整数部分为3,
它的小数部分是 .
应用迁移 拓展思维
三
分析:
分析:
如图3个网格都是由边长为1的小正方形组成.
(1)图①中阴影正方形的顶点在网络的格点上,这个阴影正方形的面积
为 ,则这个正方形的边长为 .
(2)图②中阴影正方形的顶点在网络的格点上,这个阴影正方形的面积
为 ,则这个正方形的边长为 .
问题
图①
图②
图③
问题二:怎么进行开方运算?
能否在数轴上准确地表示 呢?
应用迁移 拓展思维
三
分析:要在4×4网格中画出面积为10的正方形,网格总面积为16,可见减去面积为6,分为4个直角三角形,每个直角三角形面积均为1.5,且顶点在格点上,因此分割线为3×1网格的对角线.
问题
(3)根据以上两题的启发,你能在图③网格中画出面积为10,
并且顶点在格点上的正方形吗?
图③
问题二:怎么进行开方运算?
能否在数轴上准确地表示 呢?
应用迁移 拓展思维
三
(4)请在数轴上表示实数 并比较它们的大小
(用“<”连接).
0
1
-1
5
-2
-3
-4
3
4
2
3.“图算”
问题
图①
图②
图③
一一对应
实数
数轴上的点
在数轴上表示的实数,
右边的数总比左边的数大.
问题二:怎么进行开方运算?
数
形
表示
能否在数轴上准确地表示 呢?
(数形结合思想)
应用迁移 拓展思维
三
4.混合算
运算法则
有理数
实 数
计算下列各式:
实数运算顺序:
先算乘方和开方,再算乘除,最后算加减.如果遇到括号,则先进行括号里的运算.
问题二:怎么进行开方运算?
解 原式
解 原式
解 原式
应用迁移 拓展思维
三
平方根
立方根
实数
实数的运算
实数在数轴上的表示
什么是开方运算?
实数的概念与数系的发展
怎么进行开方运算?
开立方
“图算”
反思小结 深化思维
四
有理数
实数
正整数,0,正分数
中心问题
开立方
开平方
互逆
运算
乘方
开方
估算
心算
混合算
(数形结合思想)
同学们,再见
第六章 实数的复习
问题一 什么是开方运算?
问题二 怎么进行开方运算?
问题驱动 激活思维
一
中心问题:
运算 运算符号 运算中两数 结果
+
-
×
加
减
除
乘
加数
和
被减数,减数
因数
差
积
被除数,除数
商
互逆
互逆
目前为止我们学习了哪些运算?
乘方
开方
问题一:什么是开方运算?
知识梳理 建构思维
二
乘方 开方 运算 运算符号 运算中两数 结果 运算 运算 符号 运算中两数 结果
底数,指数
底数,指数
二次幂
三次幂
(已知底数和指数求幂)
问题一:什么是开方运算?
平方
立方
开平方
被开方数(a)
根指数(2)
平方根
(二次方根)
=a
x=
开立方
被开方数(a)
根指数(3)
立方根
(三次方根)
(已知幂和指数求底数)
开n次方运算:求一个数的n次方根的运算
互逆
知识梳理 建构思维
二
被开方数 平方根 算术平方根 立方根
问题二:怎么进行开方运算?
64
-27
0
没有
没有
完成下表:
4
0
0
0
±8
8
-3
1.任何数都有平方根,立方根吗?有几个?它们之间有什么关系?
1.心算
定义
问题
知识梳理 建构思维
二
三根比较 平方根 算术平方根 立方根
性质 正数
零
负数
是它本身的数
归纳1:平方根,算术平方根,立方根的特征
1.心算
定义
互为相反数(两个)
正数
正数(一个)
0
0
0
没有
没有
负数(一个)
0
0,1
0,±1
问题二:怎么进行开方运算?
知识梳理 建构思维
二
被开方数 平方根 算术平方根 立方根
2.你还能写出其他形式的无理数吗?
常见的无理数主要有哪几种形式?
64
-27
10
0
没有
没有
完成下表:
4
0
0
0
±8
8
-3
1.心算
定义
0.101001…(两个1之间依次多一个0)……)
归纳2:无理数常见呈现形式
③有规律又不循环的小数
①开方开不尽的数
② π及含π的数
问题二:怎么进行开方运算?
问题
知识梳理 建构思维
二
归纳3:数系的发展与实数的分类
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
正无理数
负无理数
有限小数及无限循环小数
无限不循环小数
问题二:怎么进行开方运算?
知识梳理 建构思维
二
,
属于有理数的有 ;
属于无理数的有 ;
属于负实数的有 ;
属于分数的有 .
问题二:怎么进行开方运算?
,0.262262226……
对实数进行分类时能化简的应先化简再判断;
是无理数不属于分数.
温馨提示:
归纳3:数系的发展与实数的分类
知识梳理 建构思维
二
问题
0.262262226……(两个6之间依次多一个2)中,)
被开方数 平方根 算术平方根 立方根
64
-27
10
0
没有
没有
完成下表:
4
0
0
0
±8
8
-3
问题二:怎么进行开方运算?
问题
3. 大概有多大呢?
2.估算
应用迁移 拓展思维
三
(2) 的整数部分是 ,小数部分是 .
2.估算
逼近法
问题
2
问题二:怎么进行开方运算?
(1) 界于哪两个相邻的整数之间?
可见 的整数部分为3,
它的小数部分是 .
应用迁移 拓展思维
三
分析:
分析:
如图3个网格都是由边长为1的小正方形组成.
(1)图①中阴影正方形的顶点在网络的格点上,这个阴影正方形的面积
为 ,则这个正方形的边长为 .
(2)图②中阴影正方形的顶点在网络的格点上,这个阴影正方形的面积
为 ,则这个正方形的边长为 .
问题
图①
图②
图③
问题二:怎么进行开方运算?
能否在数轴上准确地表示 呢?
应用迁移 拓展思维
三
分析:要在4×4网格中画出面积为10的正方形,网格总面积为16,可见减去面积为6,分为4个直角三角形,每个直角三角形面积均为1.5,且顶点在格点上,因此分割线为3×1网格的对角线.
问题
(3)根据以上两题的启发,你能在图③网格中画出面积为10,
并且顶点在格点上的正方形吗?
图③
问题二:怎么进行开方运算?
能否在数轴上准确地表示 呢?
应用迁移 拓展思维
三
(4)请在数轴上表示实数 并比较它们的大小
(用“<”连接).
0
1
-1
5
-2
-3
-4
3
4
2
3.“图算”
问题
图①
图②
图③
一一对应
实数
数轴上的点
在数轴上表示的实数,
右边的数总比左边的数大.
问题二:怎么进行开方运算?
数
形
表示
能否在数轴上准确地表示 呢?
(数形结合思想)
应用迁移 拓展思维
三
4.混合算
运算法则
有理数
实 数
计算下列各式:
实数运算顺序:
先算乘方和开方,再算乘除,最后算加减.如果遇到括号,则先进行括号里的运算.
问题二:怎么进行开方运算?
解 原式
解 原式
解 原式
应用迁移 拓展思维
三
平方根
立方根
实数
实数的运算
实数在数轴上的表示
什么是开方运算?
实数的概念与数系的发展
怎么进行开方运算?
开立方
“图算”
反思小结 深化思维
四
有理数
实数
正整数,0,正分数
中心问题
开立方
开平方
互逆
运算
乘方
开方
估算
心算
混合算
(数形结合思想)
同学们,再见
