初中数学人教版七年级下册 第五章 相交线与平行线 小结课件(16张PPT)
文档属性
| 名称 | 初中数学人教版七年级下册 第五章 相交线与平行线 小结课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 786.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 19:13:52 | ||
图片预览

文档简介
(共16张PPT)
第5章 小结
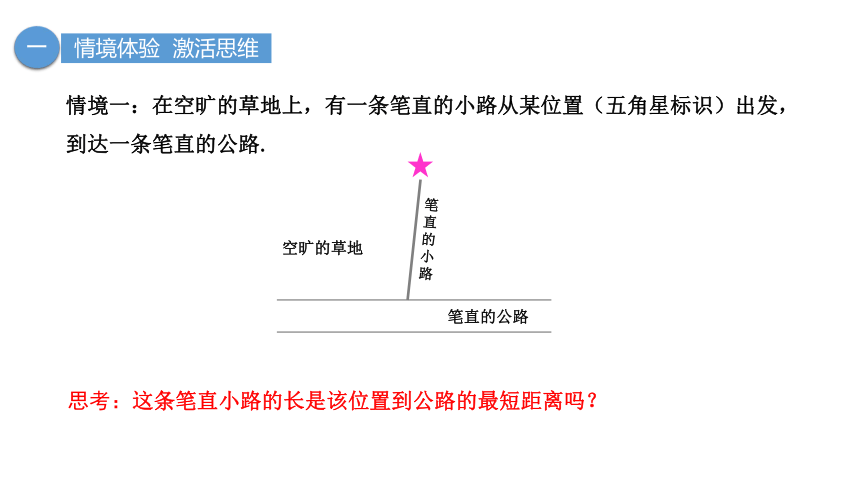
思考:这条笔直小路的长是该位置到公路的最短距离吗?
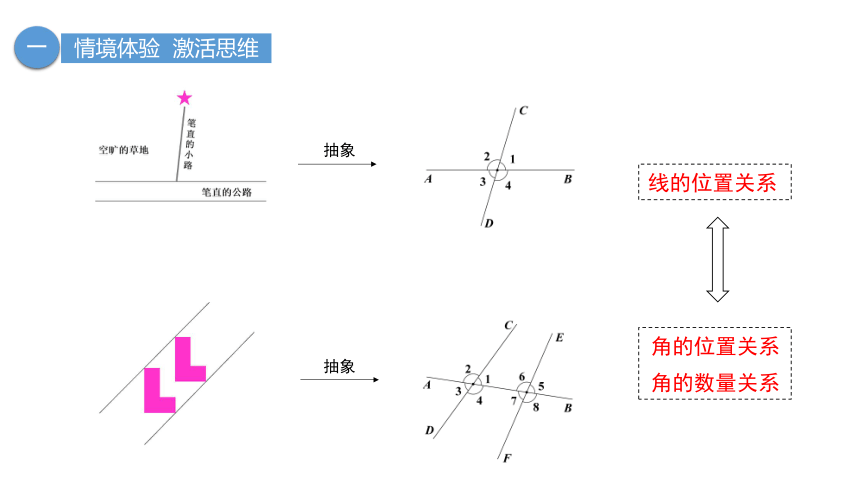
情境一:在空旷的草地上,有一条笔直的小路从某位置(五角星标识)出发,到达一条笔直的公路.
空旷的草地
笔直的公路
笔
直
的
小
路
情境体验 激活思维
一
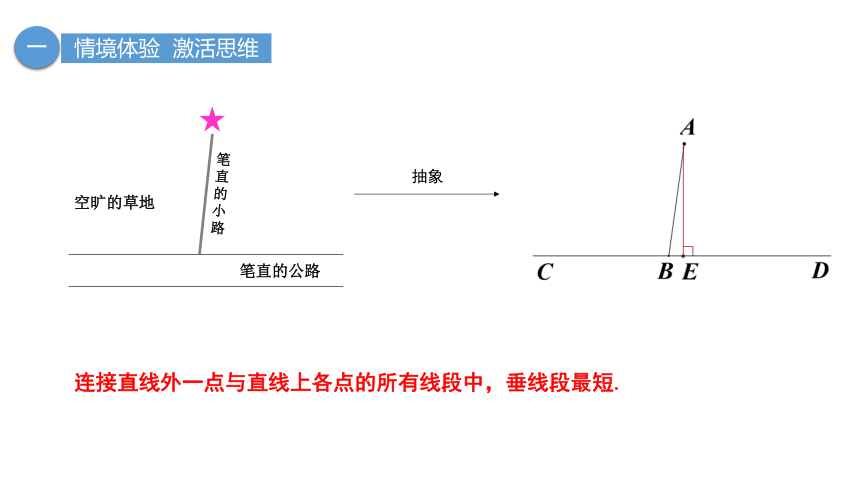
连接直线外一点与直线上各点的所有线段中,垂线段最短.
空旷的草地
笔直的公路
笔
直
的
小
路
情境体验 激活思维
一
抽象
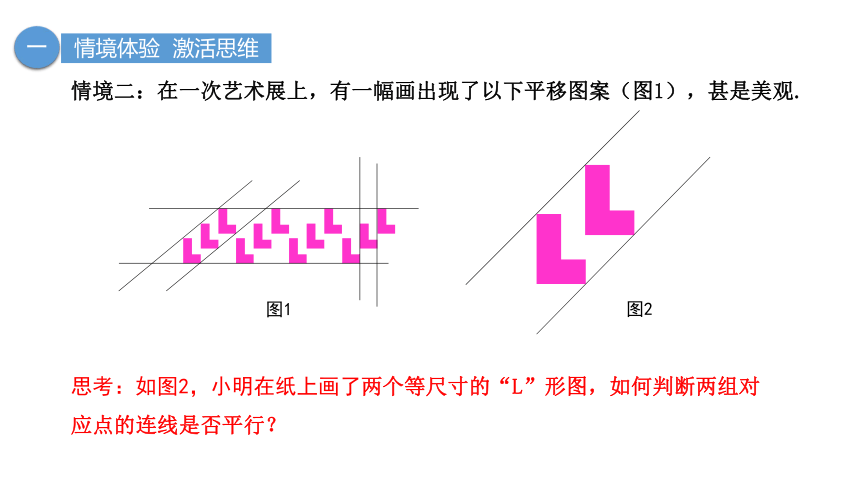
思考:如图2,小明在纸上画了两个等尺寸的“L”形图,如何判断两组对应点的连线是否平行?
情境二:在一次艺术展上,有一幅画出现了以下平移图案(图1),甚是美观.
图1
图2
情境体验 激活思维
一
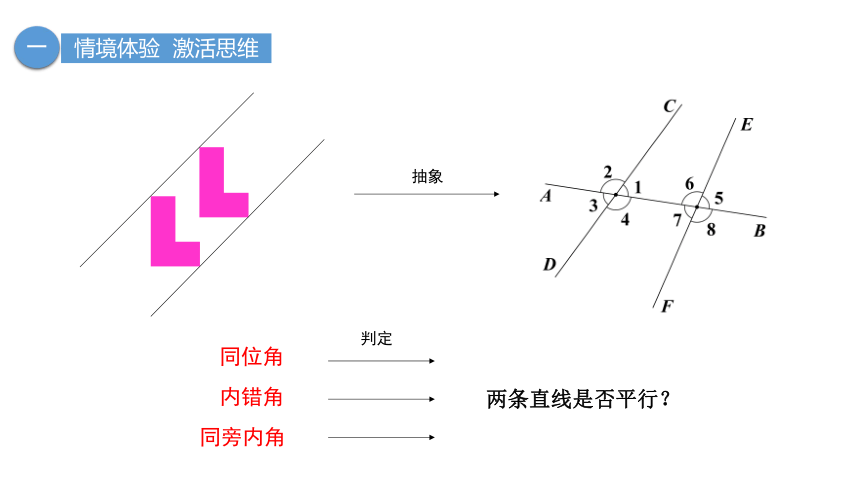
同位角
情境体验 激活思维
一
抽象
内错角
同旁内角
两条直线是否平行?
判定
角的位置关系
线的位置关系
角的数量关系
抽象
抽象
情境体验 激活思维
一
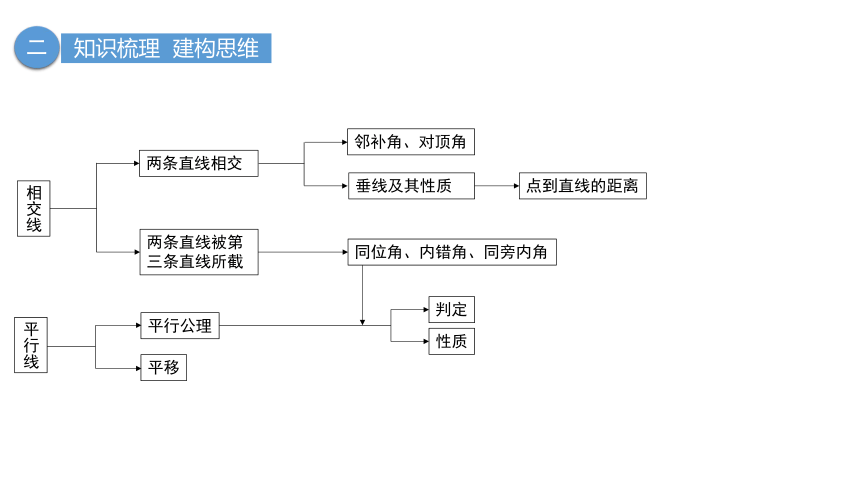
相交线
平行线
两条直线相交
两条直线被第三条直线所截
邻补角、对顶角
垂线及其性质
点到直线的距离
同位角、内错角、同旁内角
平行公理
平移
判定
性质
知识梳理 建构思维
二
1.如图,两条直线a,b相交,如果∠2=3∠1,那么∠3的度数是( )
A.30° B.45° C.60° D.135°
2.如图,点E在AC的延长线上,下列条件中不能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠A=∠DCE D.∠1+∠3+∠D=180°
知识梳理 建构思维
二
第1题
第2题
B
B
3.完成下面的证明.
如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.
求证:OE⊥OF.
证明:∵直线AB,CD相交于点O(已知),
∴∠AOD+∠BOD=180°(平角的定义).
∵ OE平分∠AOD,OF平分∠BOD(已知),
∴∠EOD= ∠AOD,∠DOF= ∠BOD(角平分线的定义).
∴∠EOF=∠EOD+∠DOF= °.
∴OE⊥OF ( ).
知识梳理 建构思维
二
90
垂直的定义
4.请指出命题“两条边分别平行的两个角相等”的题设和结论,并判断该命题是真命题还是假命题,如果是假命题,举出一个反例.
知识梳理 建构思维
二
反例
题设:有两个角,它们的两条边分别平行.
结论:这两个角相等.
例 如图,在三角形ABC中,CD⊥AB于点D,EF⊥AB于点F,交BC于点E,G是AC上一点,且满足∠ADG=∠B.
求证:∠1=∠2.
例
题
演
练
应用迁移 拓展思维
三
CD⊥AB, EF⊥AB
EF∥CD
∠ADG=∠B
DG∥BC
∠1=∠DCB
∠2=∠DCB
∠1=∠2
题设
结论
平行线的判定
平行线的性质
例 如图,在三角形ABC中,CD⊥AB于点D,EF⊥AB于点F,交BC于点E,G是AC上一点,且满足∠ADG=∠B.
求证:∠1=∠2.
例
题
演
练
应用迁移 拓展思维
三
证明:∵CD⊥AB, EF⊥AB(已知),
∴∠EFD+∠CDF=90°+90°=180°(垂直的意义),
∴EF∥CD(同旁内角互补,两直线平行),
∴∠1=∠DCB(两直线平行,同位角相等).
∵∠ADG=∠B (已知),
∴DG∥BC(同位角相等,两直线平行),
∴∠2=∠DCB(两直线平行,内错角相等).
∴∠1=∠2(等量代换).
生
长
拓
学
变式 如图,在例题图的基础上,请从以下语句:①CD⊥AB,EF⊥AB ;②∠ADG=∠B;③∠1=∠2. 选择两个为题设,其余一个为结论,写一个区别于例题的真命题,并写出证明过程.
应用迁移 拓展思维
三
题设:①和③,结论:②.
证明:∵CD⊥AB, EF⊥AB(已知),
∴∠EFD+∠CDF=90°+90°=180°(垂直的意义),
∴EF∥CD(同旁内角互补,两直线平行),
∴∠1=∠DCB(两直线平行,同位角相等).
∵∠1=∠2(已知),
∴∠2=∠DCB (等量代换),
∴DG∥BC(内错角相等,两直线平行),
∴∠ADG=∠B(两直线平行,同位角相等).
如图,该图案是由字母“MATH” 平移形成,视觉上具有立体感,整个图案具有艺术效果.
应用迁移 拓展思维
三
生
长
拓
学
请在方格纸上画一个格点图案,尝试利用平移的方法画出它具体立体感的图案,变换不同的长度和方向多试几次,你认为哪一种更具艺术效果呢?
相交线
平行线
两条直线相交
两条直线被第三条直线所截
邻补角、对顶角
垂线及其性质
点到直线的距离
同位角、内错角、同旁内角
平行公理
平移
判定
性质
角的位置关系
线的位置关系
角的数量关系
生活实际
抽象
应用
观察,猜想,归纳,推理
数学结论
反思总结 深化思维
四
同学们,再见
第5章 小结
思考:这条笔直小路的长是该位置到公路的最短距离吗?
情境一:在空旷的草地上,有一条笔直的小路从某位置(五角星标识)出发,到达一条笔直的公路.
空旷的草地
笔直的公路
笔
直
的
小
路
情境体验 激活思维
一
连接直线外一点与直线上各点的所有线段中,垂线段最短.
空旷的草地
笔直的公路
笔
直
的
小
路
情境体验 激活思维
一
抽象
思考:如图2,小明在纸上画了两个等尺寸的“L”形图,如何判断两组对应点的连线是否平行?
情境二:在一次艺术展上,有一幅画出现了以下平移图案(图1),甚是美观.
图1
图2
情境体验 激活思维
一
同位角
情境体验 激活思维
一
抽象
内错角
同旁内角
两条直线是否平行?
判定
角的位置关系
线的位置关系
角的数量关系
抽象
抽象
情境体验 激活思维
一
相交线
平行线
两条直线相交
两条直线被第三条直线所截
邻补角、对顶角
垂线及其性质
点到直线的距离
同位角、内错角、同旁内角
平行公理
平移
判定
性质
知识梳理 建构思维
二
1.如图,两条直线a,b相交,如果∠2=3∠1,那么∠3的度数是( )
A.30° B.45° C.60° D.135°
2.如图,点E在AC的延长线上,下列条件中不能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠A=∠DCE D.∠1+∠3+∠D=180°
知识梳理 建构思维
二
第1题
第2题
B
B
3.完成下面的证明.
如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.
求证:OE⊥OF.
证明:∵直线AB,CD相交于点O(已知),
∴∠AOD+∠BOD=180°(平角的定义).
∵ OE平分∠AOD,OF平分∠BOD(已知),
∴∠EOD= ∠AOD,∠DOF= ∠BOD(角平分线的定义).
∴∠EOF=∠EOD+∠DOF= °.
∴OE⊥OF ( ).
知识梳理 建构思维
二
90
垂直的定义
4.请指出命题“两条边分别平行的两个角相等”的题设和结论,并判断该命题是真命题还是假命题,如果是假命题,举出一个反例.
知识梳理 建构思维
二
反例
题设:有两个角,它们的两条边分别平行.
结论:这两个角相等.
例 如图,在三角形ABC中,CD⊥AB于点D,EF⊥AB于点F,交BC于点E,G是AC上一点,且满足∠ADG=∠B.
求证:∠1=∠2.
例
题
演
练
应用迁移 拓展思维
三
CD⊥AB, EF⊥AB
EF∥CD
∠ADG=∠B
DG∥BC
∠1=∠DCB
∠2=∠DCB
∠1=∠2
题设
结论
平行线的判定
平行线的性质
例 如图,在三角形ABC中,CD⊥AB于点D,EF⊥AB于点F,交BC于点E,G是AC上一点,且满足∠ADG=∠B.
求证:∠1=∠2.
例
题
演
练
应用迁移 拓展思维
三
证明:∵CD⊥AB, EF⊥AB(已知),
∴∠EFD+∠CDF=90°+90°=180°(垂直的意义),
∴EF∥CD(同旁内角互补,两直线平行),
∴∠1=∠DCB(两直线平行,同位角相等).
∵∠ADG=∠B (已知),
∴DG∥BC(同位角相等,两直线平行),
∴∠2=∠DCB(两直线平行,内错角相等).
∴∠1=∠2(等量代换).
生
长
拓
学
变式 如图,在例题图的基础上,请从以下语句:①CD⊥AB,EF⊥AB ;②∠ADG=∠B;③∠1=∠2. 选择两个为题设,其余一个为结论,写一个区别于例题的真命题,并写出证明过程.
应用迁移 拓展思维
三
题设:①和③,结论:②.
证明:∵CD⊥AB, EF⊥AB(已知),
∴∠EFD+∠CDF=90°+90°=180°(垂直的意义),
∴EF∥CD(同旁内角互补,两直线平行),
∴∠1=∠DCB(两直线平行,同位角相等).
∵∠1=∠2(已知),
∴∠2=∠DCB (等量代换),
∴DG∥BC(内错角相等,两直线平行),
∴∠ADG=∠B(两直线平行,同位角相等).
如图,该图案是由字母“MATH” 平移形成,视觉上具有立体感,整个图案具有艺术效果.
应用迁移 拓展思维
三
生
长
拓
学
请在方格纸上画一个格点图案,尝试利用平移的方法画出它具体立体感的图案,变换不同的长度和方向多试几次,你认为哪一种更具艺术效果呢?
相交线
平行线
两条直线相交
两条直线被第三条直线所截
邻补角、对顶角
垂线及其性质
点到直线的距离
同位角、内错角、同旁内角
平行公理
平移
判定
性质
角的位置关系
线的位置关系
角的数量关系
生活实际
抽象
应用
观察,猜想,归纳,推理
数学结论
反思总结 深化思维
四
同学们,再见
