第五章 相交线与平行线 数学活动课件(18张PPT)人教版数学七年级下册
文档属性
| 名称 | 第五章 相交线与平行线 数学活动课件(18张PPT)人教版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 27.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 19:39:50 | ||
图片预览

文档简介
(共18张PPT)
第五章 相交线与平行线
数学活动
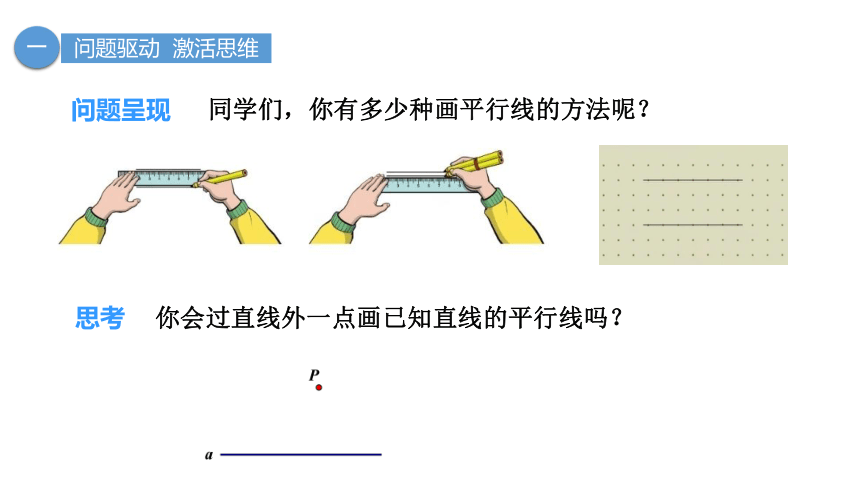
同学们,你有多少种画平行线的方法呢?
问题呈现
问题驱动 激活思维
一
思考 你会过直线外一点画已知直线的平行线吗?
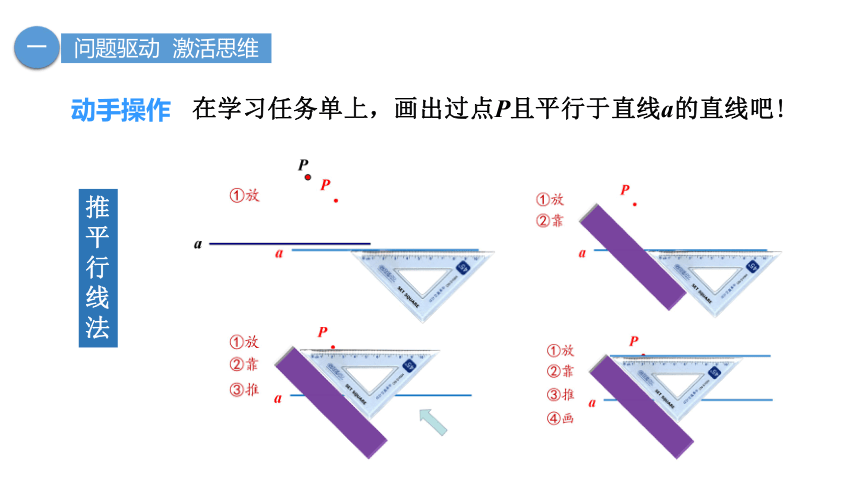
在学习任务单上,画出过点P且平行于直线a的直线吧!
动手操作
问题驱动 激活思维
一
推平行线法
问题驱动 激活思维
一
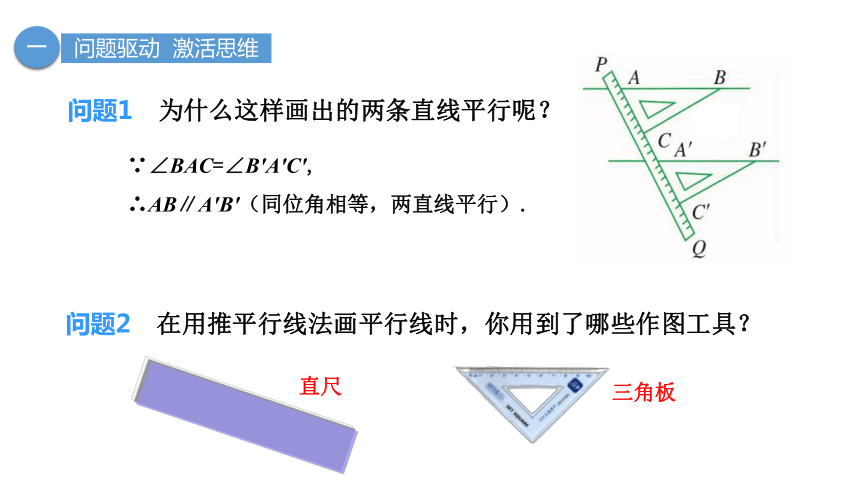
问题1 为什么这样画出的两条直线平行呢?
∵∠BAC=∠B′A′C′,
∴AB∥A′B′(同位角相等,两直线平行).
问题2 在用推平行线法画平行线时,你用到了哪些作图工具?
三角板
直尺
问题驱动 激活思维
一
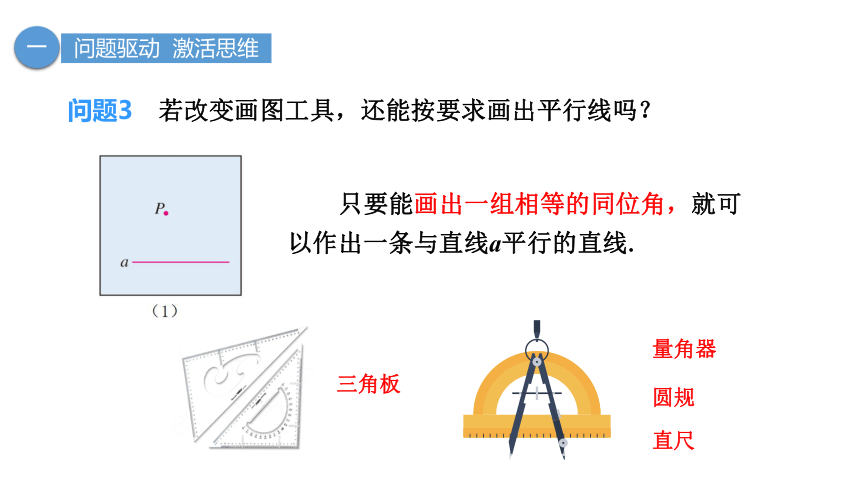
问题3 若改变画图工具,还能按要求画出平行线吗?
只要能画出一组相等的同位角,就可以作出一条与直线a平行的直线.
三角板
量角器
直尺
圆规
探究新知 建构思维
二
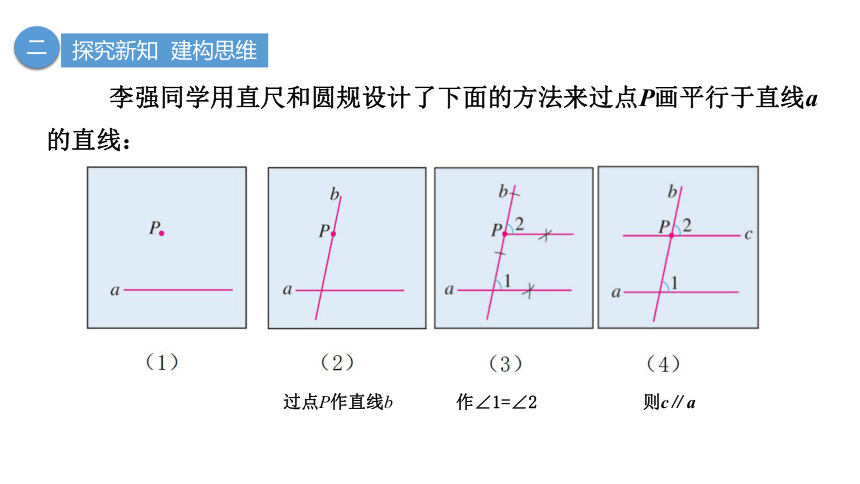
李强同学用直尺和圆规设计了下面的方法来过点P画平行于直线a的直线:
过点P作直线b
作∠1=∠2
则c∥a
探究新知 建构思维
二
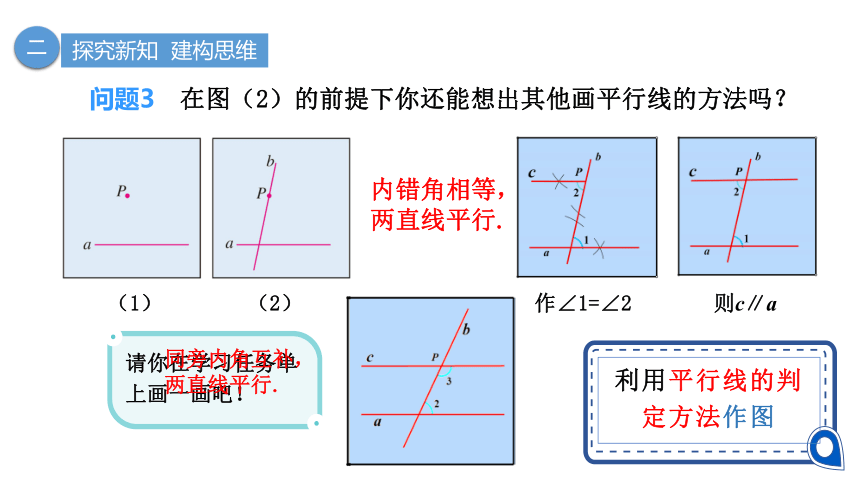
问题3 在图(2)的前提下你还能想出其他画平行线的方法吗?
(1)
(2)
请你在学习任务单上画一画吧!
内错角相等,两直线平行.
作∠1=∠2
则c∥a
同旁内角互补,两直线平行.
利用平行线的判定方法作图
探究新知 建构思维
二
问题4 除了利用平行线的判定方法作图,你还能想出其他画平行线的方法吗?
思考 观察这些图形,你能发现新的画平行线的方法吗?
可以构造含有平行边的图形得到平行线.
探究新知 建构思维
二
张明的画法如下:
问题5 观察图(4),猜想张明构造出了一个什么图形?
作PQ⊥a
作l⊥a,取RS=PQ.
连接PS,则b∥a.
长方形
探究新知 建构思维
二
同学们,你一定发现了很多其他构图的方法,记得与同伴分享哦!
问题6 根据张明的做法,想一想还能怎样构造平行线呢?
作PQ=AB,BQ=AP,则四边形ABQP是平行四边形.
则PQ∥AB.
利用平行四边形的特征构图
探究新知 建构思维
二
问题7 若没有画图工具,如何得出过点P且平行于直线a的直线?
思考1 你可以较容易地折出与直线a有怎样位置关系的折痕?
让折痕与直线a平行.
l
折出来
折痕垂直于直线a.
探究新知 建构思维
二
思考2 在这基础上再怎么折,可折出与直线a平行的折痕?
探究新知 建构思维
二
王玲想出了下面的方法折出平行线:
沿着过点P的折痕将直线a对折
打开,过点P将折痕对折,得到第二条折痕
第二条折痕与直线a平行
探究新知 建构思维
二
∵a⊥c,b⊥c,
∴a∥b.
结论 在同一平面内,垂直于同一条直线的两条直线互相平行.
利用平行线的
判定折纸
探究新知 建构思维
二
利用平行线的判定作图
A
利用平行四边形的特征构图
利用平行线的判定折纸
B
C
平行线的画法
过直线外一点画已知直线的平行线
探究新知 建构思维
二
方向:向上
距离:正方形的边长
方向:向右
距离:正方形 的边长
曲线平移
平面平移
问题10 类似地,你能用平移设计一些图案吗?
平面的平移
探究新知 建构思维
二
梳理小结 深化思维
三
数学活动
平行线的不同画法
利用平行线的判定作图
利用平行四边形的特征构图
利用平行线的判定折纸
设计美丽的图案
曲线平移成平面
平面平移成图案
观察猜想
动手操作
第五章 相交线与平行线
数学活动
同学们,你有多少种画平行线的方法呢?
问题呈现
问题驱动 激活思维
一
思考 你会过直线外一点画已知直线的平行线吗?
在学习任务单上,画出过点P且平行于直线a的直线吧!
动手操作
问题驱动 激活思维
一
推平行线法
问题驱动 激活思维
一
问题1 为什么这样画出的两条直线平行呢?
∵∠BAC=∠B′A′C′,
∴AB∥A′B′(同位角相等,两直线平行).
问题2 在用推平行线法画平行线时,你用到了哪些作图工具?
三角板
直尺
问题驱动 激活思维
一
问题3 若改变画图工具,还能按要求画出平行线吗?
只要能画出一组相等的同位角,就可以作出一条与直线a平行的直线.
三角板
量角器
直尺
圆规
探究新知 建构思维
二
李强同学用直尺和圆规设计了下面的方法来过点P画平行于直线a的直线:
过点P作直线b
作∠1=∠2
则c∥a
探究新知 建构思维
二
问题3 在图(2)的前提下你还能想出其他画平行线的方法吗?
(1)
(2)
请你在学习任务单上画一画吧!
内错角相等,两直线平行.
作∠1=∠2
则c∥a
同旁内角互补,两直线平行.
利用平行线的判定方法作图
探究新知 建构思维
二
问题4 除了利用平行线的判定方法作图,你还能想出其他画平行线的方法吗?
思考 观察这些图形,你能发现新的画平行线的方法吗?
可以构造含有平行边的图形得到平行线.
探究新知 建构思维
二
张明的画法如下:
问题5 观察图(4),猜想张明构造出了一个什么图形?
作PQ⊥a
作l⊥a,取RS=PQ.
连接PS,则b∥a.
长方形
探究新知 建构思维
二
同学们,你一定发现了很多其他构图的方法,记得与同伴分享哦!
问题6 根据张明的做法,想一想还能怎样构造平行线呢?
作PQ=AB,BQ=AP,则四边形ABQP是平行四边形.
则PQ∥AB.
利用平行四边形的特征构图
探究新知 建构思维
二
问题7 若没有画图工具,如何得出过点P且平行于直线a的直线?
思考1 你可以较容易地折出与直线a有怎样位置关系的折痕?
让折痕与直线a平行.
l
折出来
折痕垂直于直线a.
探究新知 建构思维
二
思考2 在这基础上再怎么折,可折出与直线a平行的折痕?
探究新知 建构思维
二
王玲想出了下面的方法折出平行线:
沿着过点P的折痕将直线a对折
打开,过点P将折痕对折,得到第二条折痕
第二条折痕与直线a平行
探究新知 建构思维
二
∵a⊥c,b⊥c,
∴a∥b.
结论 在同一平面内,垂直于同一条直线的两条直线互相平行.
利用平行线的
判定折纸
探究新知 建构思维
二
利用平行线的判定作图
A
利用平行四边形的特征构图
利用平行线的判定折纸
B
C
平行线的画法
过直线外一点画已知直线的平行线
探究新知 建构思维
二
方向:向上
距离:正方形的边长
方向:向右
距离:正方形 的边长
曲线平移
平面平移
问题10 类似地,你能用平移设计一些图案吗?
平面的平移
探究新知 建构思维
二
梳理小结 深化思维
三
数学活动
平行线的不同画法
利用平行线的判定作图
利用平行四边形的特征构图
利用平行线的判定折纸
设计美丽的图案
曲线平移成平面
平面平移成图案
观察猜想
动手操作
