5.2.2 平行线的判定 课件(15张PPT)人教版数学七年级下册
文档属性
| 名称 | 5.2.2 平行线的判定 课件(15张PPT)人教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 684.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第五章 相交线与平行线
5.2 平行线及其判定
5.2.2 平行线的判定
人教版数学 七年级下册
理解平行线的判定方法.
平行线的判定方法的应用.
理解平行线的判定方法(1)(2)(3).
学习目标
人教版数学 七年级下册教学PPT课件
怎么判断同一平面内的两条直线是否平行呢?
可以直接根据平行的定义
同一平面内,两条直线如果不相交,就一定平行.
想一想,这种方法有什么弊端?
由于直线可以无限延伸,所以检验它们是否相交往往有困难.
那么,有没有其他判定方法呢?
复习导入
人教版数学 七年级下册教学PPT课件
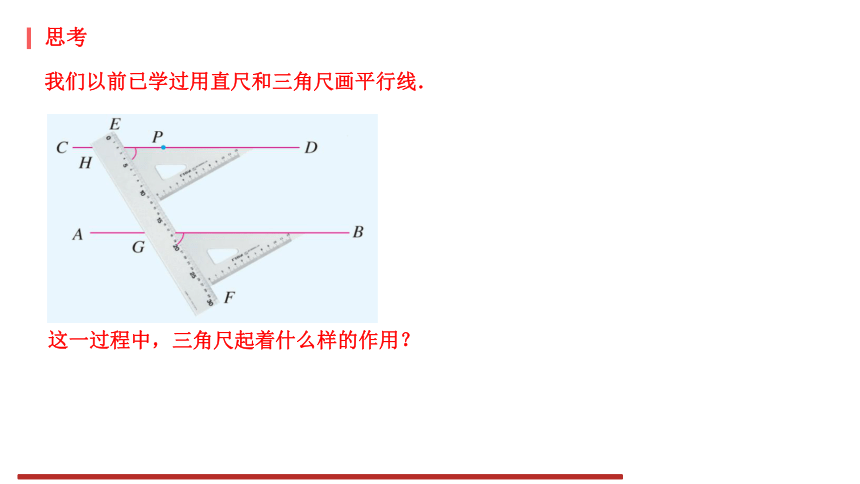
思考
这一过程中,三角尺起着什么样的作用?
我们以前已学过用直尺和三角尺画平行线.
人教版数学 七年级下册教学PPT课件
思考
可以看出,画直线AB的平行线CD,实际上是过点P画与∠2相等的∠1,
而∠2和∠1正是直线AB,CD被直线EF截得的同位角,
这说明,如果同位角相等,那么AB∥CD.
简化一下图形
人教版数学 七年级下册教学PPT课件
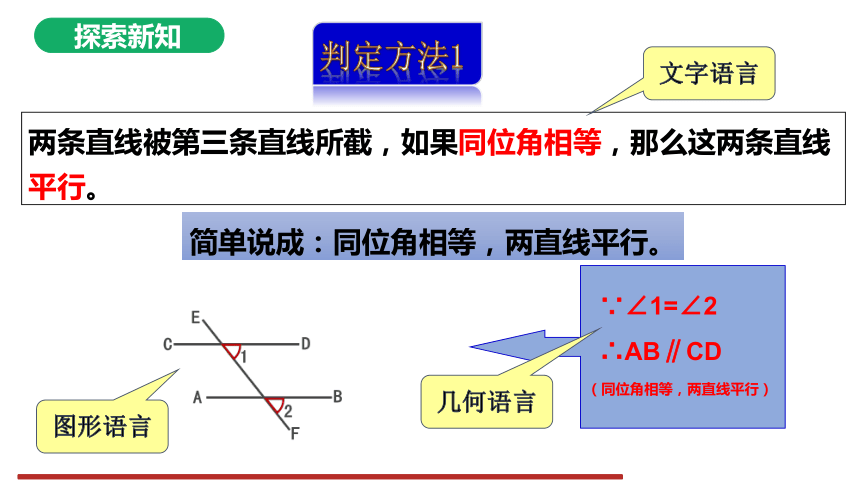
判定方法1
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
∵∠1=∠2
∴AB∥CD
(同位角相等,两直线平行)
文字语言
几何语言
图形语言
探索新知
人教版数学 七年级下册教学PPT课件
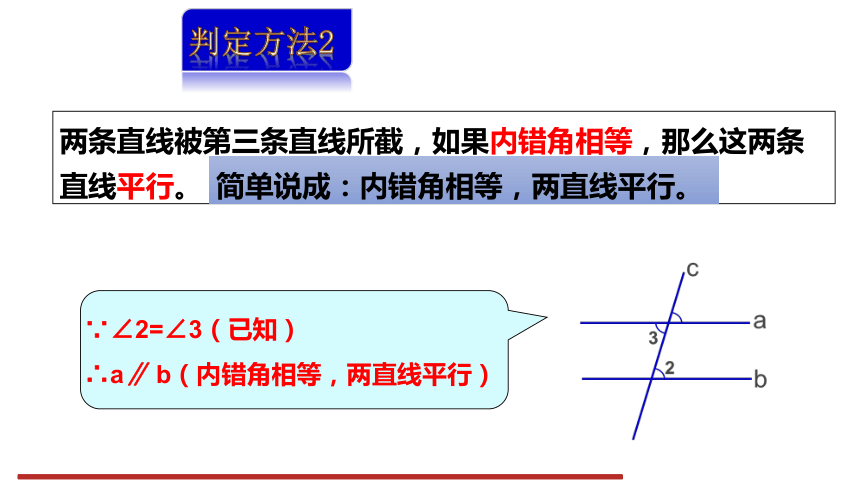
判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
∵∠2=∠3(已知)
∴a∥ b(内错角相等,两直线平行)
人教版数学 七年级下册教学PPT课件
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
∵∠2+∠4=180°(已知)
∴a∥ b(同旁内角互补,两直线平行)
人教版数学 七年级下册教学PPT课件
小例题
1.如图,已知∠1=∠2,∠3=∠4,试判断直线EF与GH是否平行,并说明理由。
解:EF与GH平行。
理由:∵∠1=∠2,∠2=∠5(已知)
∴∠1=∠5(等量代换)
又∵∠3=∠4 (已知)
∴∠1+∠3=∠4+∠5(等量加等量和相等)
即∠MEF=∠HGE
∴EF∥ HG(同位角相等,两直线平行)
人教版数学 七年级下册教学PPT课件
2.已知:如图,∠1=∠2,且BD平分∠ABC,则AB与CD的位置关系如何并说明理由?
解: AB∥ CD。
理由:∵BD平分∠ABC(已知)
∴∠2=∠DBA(角平分线的定义)
∵∠1=∠2(已知)
∴∠1=∠DBA(等量代换)
∴AB∥ CD(内错角相等,两直线平行)
小例题
人教版数学 七年级下册教学PPT课件
3.如图所示,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,那么AB与CD有怎样的位置关系?为什么?
解: AB∥ CD。
理由:∵OF平分∠EOD(已知)
∴∠FOD=∠EOD(角平分线的定义)
∵∠FOD=25°(已知)
∴∠EOD=50°
又∵∠OEB=130°(已知)
∴∠OEB+∠EOD=180°
∴AB∥ CD(同旁内角互补,两直线平行)
小例题
人教版数学 七年级下册教学PPT课件
随堂练习
人教版数学 七年级下册教学PPT课件
2.如图,(1)∠1=∠A,则GC∥AB,依据是_______________________;
内错角相等,两直线平行
(2)∠3=∠B,则 ,依据是_______________________;
同位角相等,两直线平行
(3)∠1=∠4,则 ,依据是_______________________;
内错角相等,两直线平行
(4)∠4=∠A,则 ,依据是______________________.
同位角相等,两直线平行
随堂练习
人教版数学 七年级下册教学PPT课件
1.平行线的定义:在同一平面内,不相交的直线叫做平行线.如图,直线AB与CD平行,记作:AB∥CD或CD∥AB,读作AB平行于CD或CD平行于AB.
注意:①在平行线的定义中,“同一平面”是前提,因为在空间存在既不平行又不相交的直线.
课堂小结
人教版数学 七年级下册教学PPT课件
②平行线指的是“两条直线”,而不是两条射线或线段,两条射线或线段平行,是指它们所在的两条直线平行.
③“不相交”就是说两条直线没有公共点.只有同时具备以上三个条件,才符合平行线的定义.
人教版数学 七年级下册教学PPT课件
第五章 相交线与平行线
5.2 平行线及其判定
5.2.2 平行线的判定
人教版数学 七年级下册
理解平行线的判定方法.
平行线的判定方法的应用.
理解平行线的判定方法(1)(2)(3).
学习目标
人教版数学 七年级下册教学PPT课件
怎么判断同一平面内的两条直线是否平行呢?
可以直接根据平行的定义
同一平面内,两条直线如果不相交,就一定平行.
想一想,这种方法有什么弊端?
由于直线可以无限延伸,所以检验它们是否相交往往有困难.
那么,有没有其他判定方法呢?
复习导入
人教版数学 七年级下册教学PPT课件
思考
这一过程中,三角尺起着什么样的作用?
我们以前已学过用直尺和三角尺画平行线.
人教版数学 七年级下册教学PPT课件
思考
可以看出,画直线AB的平行线CD,实际上是过点P画与∠2相等的∠1,
而∠2和∠1正是直线AB,CD被直线EF截得的同位角,
这说明,如果同位角相等,那么AB∥CD.
简化一下图形
人教版数学 七年级下册教学PPT课件
判定方法1
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
∵∠1=∠2
∴AB∥CD
(同位角相等,两直线平行)
文字语言
几何语言
图形语言
探索新知
人教版数学 七年级下册教学PPT课件
判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
∵∠2=∠3(已知)
∴a∥ b(内错角相等,两直线平行)
人教版数学 七年级下册教学PPT课件
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
∵∠2+∠4=180°(已知)
∴a∥ b(同旁内角互补,两直线平行)
人教版数学 七年级下册教学PPT课件
小例题
1.如图,已知∠1=∠2,∠3=∠4,试判断直线EF与GH是否平行,并说明理由。
解:EF与GH平行。
理由:∵∠1=∠2,∠2=∠5(已知)
∴∠1=∠5(等量代换)
又∵∠3=∠4 (已知)
∴∠1+∠3=∠4+∠5(等量加等量和相等)
即∠MEF=∠HGE
∴EF∥ HG(同位角相等,两直线平行)
人教版数学 七年级下册教学PPT课件
2.已知:如图,∠1=∠2,且BD平分∠ABC,则AB与CD的位置关系如何并说明理由?
解: AB∥ CD。
理由:∵BD平分∠ABC(已知)
∴∠2=∠DBA(角平分线的定义)
∵∠1=∠2(已知)
∴∠1=∠DBA(等量代换)
∴AB∥ CD(内错角相等,两直线平行)
小例题
人教版数学 七年级下册教学PPT课件
3.如图所示,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,那么AB与CD有怎样的位置关系?为什么?
解: AB∥ CD。
理由:∵OF平分∠EOD(已知)
∴∠FOD=∠EOD(角平分线的定义)
∵∠FOD=25°(已知)
∴∠EOD=50°
又∵∠OEB=130°(已知)
∴∠OEB+∠EOD=180°
∴AB∥ CD(同旁内角互补,两直线平行)
小例题
人教版数学 七年级下册教学PPT课件
随堂练习
人教版数学 七年级下册教学PPT课件
2.如图,(1)∠1=∠A,则GC∥AB,依据是_______________________;
内错角相等,两直线平行
(2)∠3=∠B,则 ,依据是_______________________;
同位角相等,两直线平行
(3)∠1=∠4,则 ,依据是_______________________;
内错角相等,两直线平行
(4)∠4=∠A,则 ,依据是______________________.
同位角相等,两直线平行
随堂练习
人教版数学 七年级下册教学PPT课件
1.平行线的定义:在同一平面内,不相交的直线叫做平行线.如图,直线AB与CD平行,记作:AB∥CD或CD∥AB,读作AB平行于CD或CD平行于AB.
注意:①在平行线的定义中,“同一平面”是前提,因为在空间存在既不平行又不相交的直线.
课堂小结
人教版数学 七年级下册教学PPT课件
②平行线指的是“两条直线”,而不是两条射线或线段,两条射线或线段平行,是指它们所在的两条直线平行.
③“不相交”就是说两条直线没有公共点.只有同时具备以上三个条件,才符合平行线的定义.
人教版数学 七年级下册教学PPT课件
