人教版数学七年级下册第五章相交线和平行线专项提升综合题
文档属性
| 名称 | 人教版数学七年级下册第五章相交线和平行线专项提升综合题 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学七年级下册第五章相交线和平行线专项提升综合题
一、单选题
1.如图,按各组角的位置判断不正确的是( )
A.∠1与∠4是同旁内角 B.∠3与∠4是内错角
C.∠5与∠6是同旁内角 D.∠2与∠5是同位角
2.如下图,∠1和∠2是( )
A.内错角 B.同旁内角 C.同位角 D.对项角
3.如图所示,点E在BC的延长线上,下列条件中不能判定AB//CD的是( )
A. B.
C. D.
4.在《生活中的平移现象》的数学讨论课上,小明和小红先将一块三角板描边得到,后沿着直尺方向平移,再描边得到,连接.如图,经测量发现的周长为,则四边形的周长为( )
A. B. C. D.
5.如图,,,,分别是,的平分线,于.下列结论:①;②;③;④平分;⑤.其中正确结论的个数是( )
A. B. C. D.
二、多选题
6.如图所示,下列四组条件中,能得到//的是( )
A. B.
C., D.
三、填空题
7.如图,直线a∥b,c与直线a、b分别相交于A、B两点,若∠1=50度,则∠2= 度.
8.如图,△ABC沿射线AC的方向平移,得到△CDE.若AE=6,则B,D两点的距离为 .
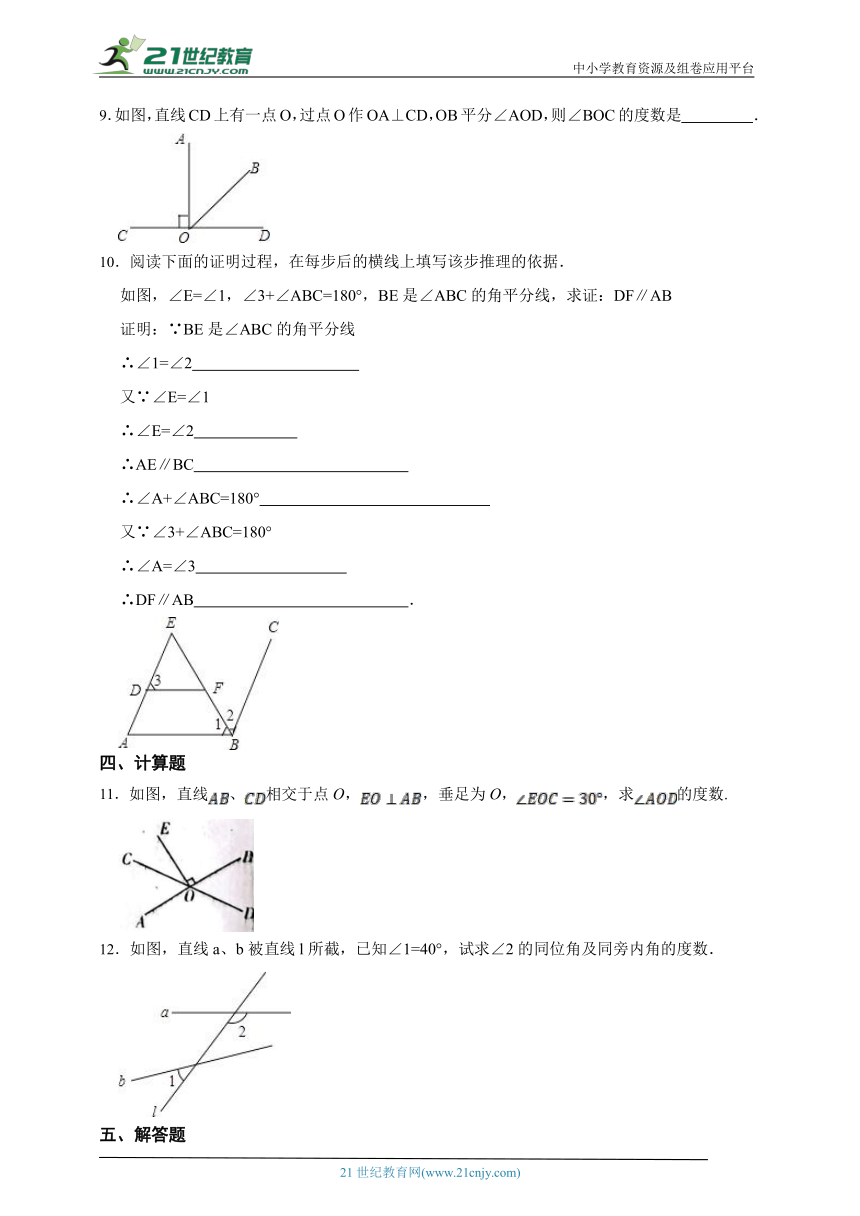
9.如图,直线CD上有一点O,过点O作OA⊥CD,OB平分∠AOD,则∠BOC的度数是 .
10.阅读下面的证明过程,在每步后的横线上填写该步推理的依据.
如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线,求证:DF∥AB
证明:∵BE是∠ABC的角平分线
∴∠1=∠2
又∵∠E=∠1
∴∠E=∠2
∴AE∥BC
∴∠A+∠ABC=180°
又∵∠3+∠ABC=180°
∴∠A=∠3
∴DF∥AB .
四、计算题
11.如图,直线、相交于点O,,垂足为O,,求的度数.
12.如图,直线a、b被直线l所截,已知∠1=40°,试求∠2的同位角及同旁内角的度数.
五、解答题
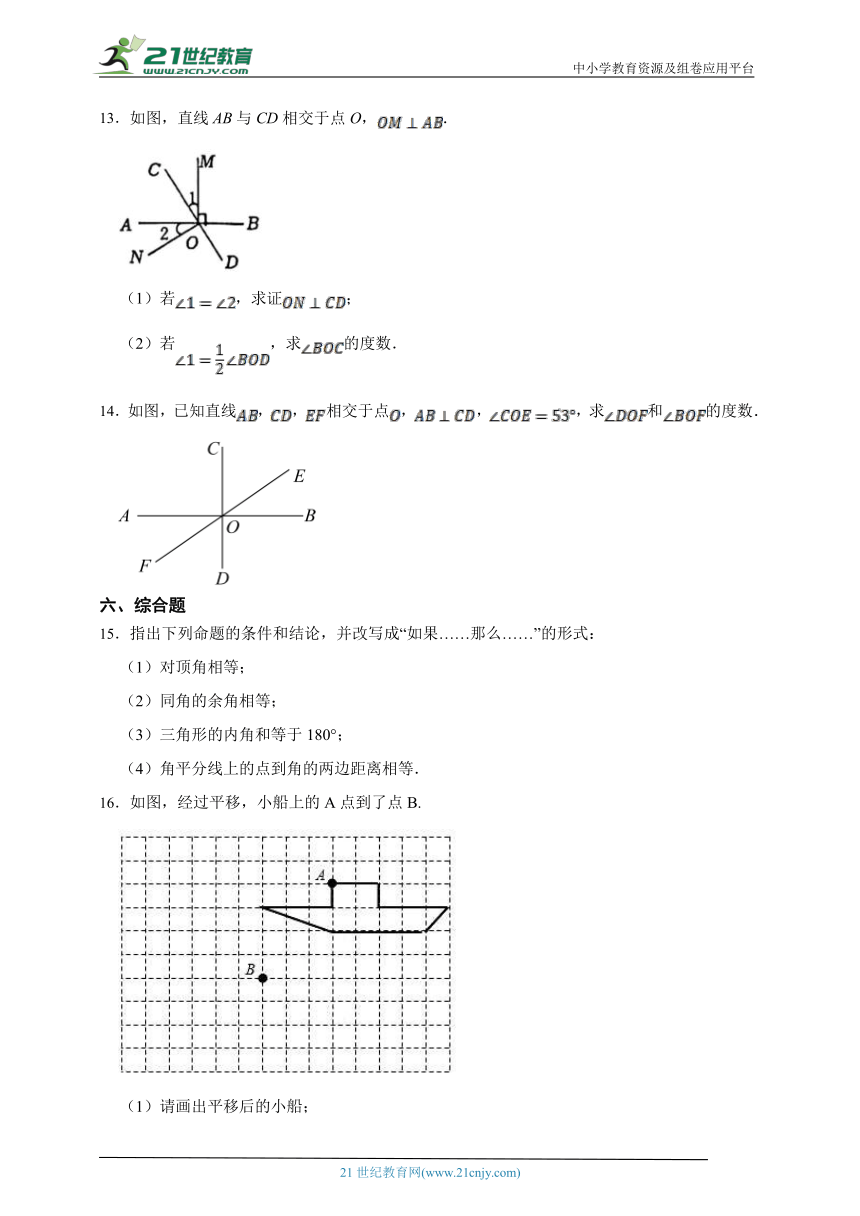
13.如图,直线AB与CD相交于点O,.
(1)若,求证;
(2)若,求的度数.
14.如图,已知直线,,相交于点,,,求和的度数.
六、综合题
15.指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
(1)对顶角相等;
(2)同角的余角相等;
(3)三角形的内角和等于180°;
(4)角平分线上的点到角的两边距离相等.
16.如图,经过平移,小船上的A点到了点B.
(1)请画出平移后的小船;
(2)该小船向 平移了 格,向 平移了 格.
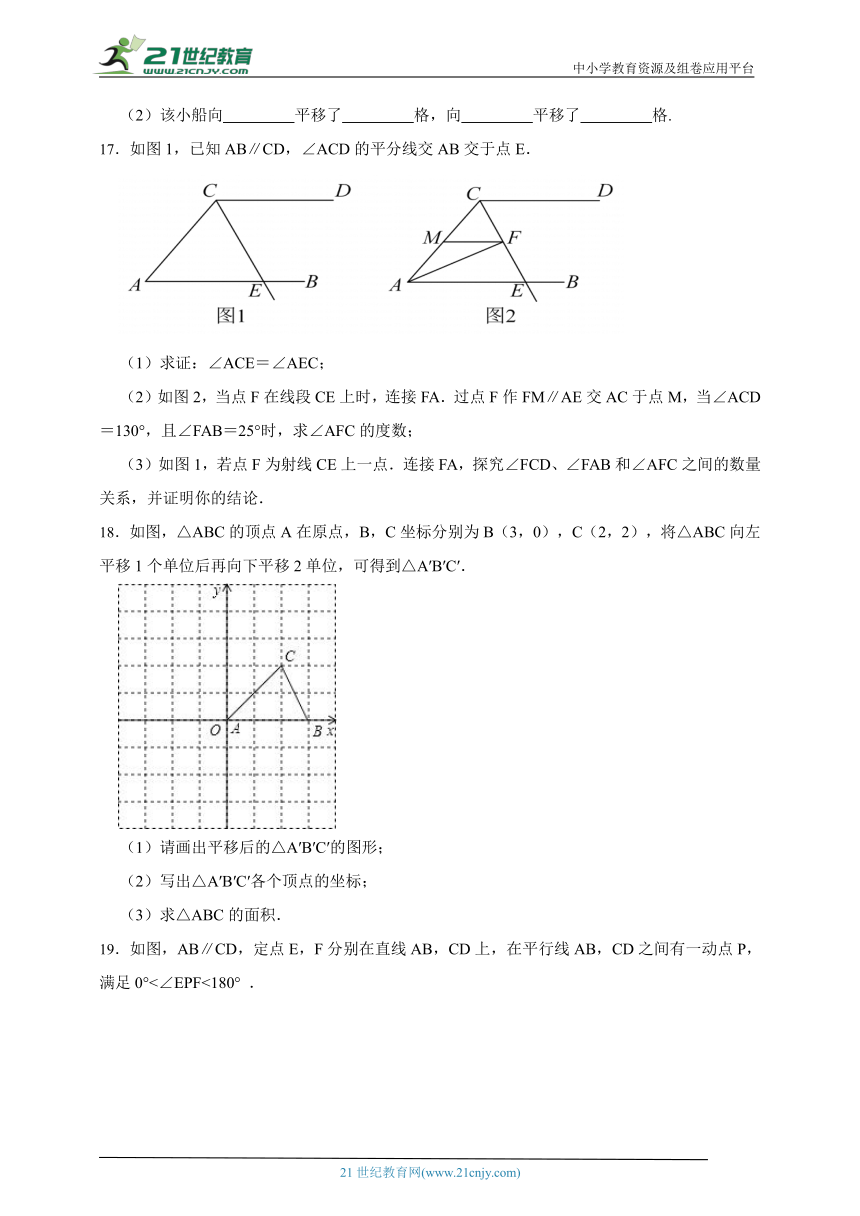
17.如图1,已知AB∥CD,∠ACD的平分线交AB交于点E.
(1)求证:∠ACE=∠AEC;
(2)如图2,当点F在线段CE上时,连接FA.过点F作FM∥AE交AC于点M,当∠ACD=130°,且∠FAB=25°时,求∠AFC的度数;
(3)如图1,若点F为射线CE上一点.连接FA,探究∠FCD、∠FAB和∠AFC之间的数量关系,并证明你的结论.
18.如图,△ABC的顶点A在原点,B,C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形;
(2)写出△A′B′C′各个顶点的坐标;
(3)求△ABC的面积.
19.如图,AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一动点P,满足0°<∠EPF<180° .
(1)试问∠AEP,∠EPF,∠PFC满足怎样的数量关系?
解:由于点P是平行线AB, CD之间的一动点,因此需要对点P的位置进行分类讨论:
如图1,当点P在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为
如图2,当点P在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为
(2)如图3,QE,QF分别平分∠PEB和∠PFD, 且点P在EF左侧.
①若∠EPF=60°,则∠EQF= .
②猜想∠EPF与∠EQF的数量关系,并说明理由;
③如图4,若∠BEQ与∠DFQ的平分线交于点Q1,∠BEQ1与∠DFQ1的平分线交于点Q2,∠BEQ2与∠DFQ2的平分线交于点Q;依次类推,则∠EPF与∠EQ2018F满足怎样的数量关系?(直接写出结果)
答案解析部分
1.【答案】C
【知识点】同位角;内错角;同旁内角
2.【答案】D
【知识点】对顶角及其性质
3.【答案】D
【知识点】平行线的判定与性质
4.【答案】B
【知识点】平移的性质;图形的平移
5.【答案】C
【知识点】角的运算;平行线的判定与性质;角平分线的定义
6.【答案】B,C
【知识点】平行线的判定
7.【答案】50
【知识点】平行线的性质
8.【答案】3
【知识点】平移的性质;图形的平移
9.【答案】135°
【知识点】垂线;角平分线的定义
10.【答案】角的平分线的定义;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;同位角相等,两直线平行
【知识点】平行线的判定与性质
11.【答案】解:
【知识点】余角、补角及其性质;垂线
12.【答案】解:
∵∠1=40°,
∴∠3=∠1=40°,4=180°﹣∠1=140°,
即∠2的同位角市140°,∠2的同旁内角是40°
【知识点】同位角;同旁内角
13.【答案】(1)证明:∵,∴,
∵,∴,∴
(2)解:∵,∴,∴,
∵,∴,∴
【知识点】角的运算;垂线
14.【答案】解:由对顶角性质可得:∠DOF=∠COE=53°,
∵CD⊥AB,
∴∠BOD=90°,
∴∠BOF=∠BOD+∠COE=90°+53°=143°,
∴∠DOF =53°,∠BOF=143°.
【知识点】角的运算;对顶角及其性质
15.【答案】(1)解:如果两个角是对顶角,那么这两个角相等,
条件:两个角是对顶角,结论:这两个角相等
(2)解:如果两个角都是同一个角的余角,那么这两个角相等.
条件:两个角都是同一个角的余角,
结论:这两个角相等
(3)解:如果三个角是一个三角形的内角,那么这三个内角和等于180°.
条件:三个角是一个三角形的内角,
结论:这三个内角和等于180°
(4)解:如果一个点在角平分线上,那么它到角两边的距离相等.
条件:一个点在角平分线上,
结论:这个点到角两边的距离相等
【知识点】定义、命题及定理的概念
16.【答案】(1)解:如图所示:
(2)下;4;左;3
【知识点】作图﹣平移
17.【答案】(1)证明:∵AB∥CD,
∴∠AEC=∠DCE,
∵CE平分∠ACD,
∴∠ACE=∠DCE,
∴∠ACE=∠AEC
(2)解:∵AB∥CD,FM∥AE,
∴∠CFM=∠DCF,∠AFM=∠FAB=25°,
∵∠ACD=130°,CE平分∠ACD
∴∠DCF=65°,
∴∠CFM=65°,
∴∠AFC=∠CFM+∠AFM=90°
(3)解:当点F在线段CE上时,过点F作FM∥AB,交AC于点M,连接AF,
∴FM∥CD,
∴∠FCD=∠MFC,
∵FM∥AB,
∴∠FAB=∠MFA,
∴∠FCD+∠FAB=∠MFC+∠MFA,
∴∠AFC=∠FCD+∠FAB.
当点F在线段CE的延长线上时,过点F作MF∥AB,连接AF,
∴FM∥CD,
∴∠FCD=∠MFC,
∵FM∥AB,
∴∠FAB=∠MFA,
∵∠MFC=∠MFA+∠AFC,
∴∠FCD=∠FAB+∠AFC.
综上,∠AFC=∠FCD+∠FAB或∠FCD=∠FAB+∠AFC.
【知识点】平行线的性质;角平分线的定义
18.【答案】(1)解:A′B′C′如图所示
(2)解:A′(﹣1,﹣2),B′(2,﹣2),C′(1,0)
(3)解:S△ABC= ×3×2=3
【知识点】作图﹣平移
19.【答案】(1)∠EPF=∠AEP+∠PFC;∠AEP+∠EPF+∠PFC=360°
(2)150°
【知识点】角的运算;平行线的判定与性质;角平分线的定义
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学七年级下册第五章相交线和平行线专项提升综合题
一、单选题
1.如图,按各组角的位置判断不正确的是( )
A.∠1与∠4是同旁内角 B.∠3与∠4是内错角
C.∠5与∠6是同旁内角 D.∠2与∠5是同位角
2.如下图,∠1和∠2是( )
A.内错角 B.同旁内角 C.同位角 D.对项角
3.如图所示,点E在BC的延长线上,下列条件中不能判定AB//CD的是( )
A. B.
C. D.
4.在《生活中的平移现象》的数学讨论课上,小明和小红先将一块三角板描边得到,后沿着直尺方向平移,再描边得到,连接.如图,经测量发现的周长为,则四边形的周长为( )
A. B. C. D.
5.如图,,,,分别是,的平分线,于.下列结论:①;②;③;④平分;⑤.其中正确结论的个数是( )
A. B. C. D.
二、多选题
6.如图所示,下列四组条件中,能得到//的是( )
A. B.
C., D.
三、填空题
7.如图,直线a∥b,c与直线a、b分别相交于A、B两点,若∠1=50度,则∠2= 度.
8.如图,△ABC沿射线AC的方向平移,得到△CDE.若AE=6,则B,D两点的距离为 .
9.如图,直线CD上有一点O,过点O作OA⊥CD,OB平分∠AOD,则∠BOC的度数是 .
10.阅读下面的证明过程,在每步后的横线上填写该步推理的依据.
如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线,求证:DF∥AB
证明:∵BE是∠ABC的角平分线
∴∠1=∠2
又∵∠E=∠1
∴∠E=∠2
∴AE∥BC
∴∠A+∠ABC=180°
又∵∠3+∠ABC=180°
∴∠A=∠3
∴DF∥AB .
四、计算题
11.如图,直线、相交于点O,,垂足为O,,求的度数.
12.如图,直线a、b被直线l所截,已知∠1=40°,试求∠2的同位角及同旁内角的度数.
五、解答题
13.如图,直线AB与CD相交于点O,.
(1)若,求证;
(2)若,求的度数.
14.如图,已知直线,,相交于点,,,求和的度数.
六、综合题
15.指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
(1)对顶角相等;
(2)同角的余角相等;
(3)三角形的内角和等于180°;
(4)角平分线上的点到角的两边距离相等.
16.如图,经过平移,小船上的A点到了点B.
(1)请画出平移后的小船;
(2)该小船向 平移了 格,向 平移了 格.
17.如图1,已知AB∥CD,∠ACD的平分线交AB交于点E.
(1)求证:∠ACE=∠AEC;
(2)如图2,当点F在线段CE上时,连接FA.过点F作FM∥AE交AC于点M,当∠ACD=130°,且∠FAB=25°时,求∠AFC的度数;
(3)如图1,若点F为射线CE上一点.连接FA,探究∠FCD、∠FAB和∠AFC之间的数量关系,并证明你的结论.
18.如图,△ABC的顶点A在原点,B,C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形;
(2)写出△A′B′C′各个顶点的坐标;
(3)求△ABC的面积.
19.如图,AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一动点P,满足0°<∠EPF<180° .
(1)试问∠AEP,∠EPF,∠PFC满足怎样的数量关系?
解:由于点P是平行线AB, CD之间的一动点,因此需要对点P的位置进行分类讨论:
如图1,当点P在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为
如图2,当点P在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为
(2)如图3,QE,QF分别平分∠PEB和∠PFD, 且点P在EF左侧.
①若∠EPF=60°,则∠EQF= .
②猜想∠EPF与∠EQF的数量关系,并说明理由;
③如图4,若∠BEQ与∠DFQ的平分线交于点Q1,∠BEQ1与∠DFQ1的平分线交于点Q2,∠BEQ2与∠DFQ2的平分线交于点Q;依次类推,则∠EPF与∠EQ2018F满足怎样的数量关系?(直接写出结果)
答案解析部分
1.【答案】C
【知识点】同位角;内错角;同旁内角
2.【答案】D
【知识点】对顶角及其性质
3.【答案】D
【知识点】平行线的判定与性质
4.【答案】B
【知识点】平移的性质;图形的平移
5.【答案】C
【知识点】角的运算;平行线的判定与性质;角平分线的定义
6.【答案】B,C
【知识点】平行线的判定
7.【答案】50
【知识点】平行线的性质
8.【答案】3
【知识点】平移的性质;图形的平移
9.【答案】135°
【知识点】垂线;角平分线的定义
10.【答案】角的平分线的定义;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等;同位角相等,两直线平行
【知识点】平行线的判定与性质
11.【答案】解:
【知识点】余角、补角及其性质;垂线
12.【答案】解:
∵∠1=40°,
∴∠3=∠1=40°,4=180°﹣∠1=140°,
即∠2的同位角市140°,∠2的同旁内角是40°
【知识点】同位角;同旁内角
13.【答案】(1)证明:∵,∴,
∵,∴,∴
(2)解:∵,∴,∴,
∵,∴,∴
【知识点】角的运算;垂线
14.【答案】解:由对顶角性质可得:∠DOF=∠COE=53°,
∵CD⊥AB,
∴∠BOD=90°,
∴∠BOF=∠BOD+∠COE=90°+53°=143°,
∴∠DOF =53°,∠BOF=143°.
【知识点】角的运算;对顶角及其性质
15.【答案】(1)解:如果两个角是对顶角,那么这两个角相等,
条件:两个角是对顶角,结论:这两个角相等
(2)解:如果两个角都是同一个角的余角,那么这两个角相等.
条件:两个角都是同一个角的余角,
结论:这两个角相等
(3)解:如果三个角是一个三角形的内角,那么这三个内角和等于180°.
条件:三个角是一个三角形的内角,
结论:这三个内角和等于180°
(4)解:如果一个点在角平分线上,那么它到角两边的距离相等.
条件:一个点在角平分线上,
结论:这个点到角两边的距离相等
【知识点】定义、命题及定理的概念
16.【答案】(1)解:如图所示:
(2)下;4;左;3
【知识点】作图﹣平移
17.【答案】(1)证明:∵AB∥CD,
∴∠AEC=∠DCE,
∵CE平分∠ACD,
∴∠ACE=∠DCE,
∴∠ACE=∠AEC
(2)解:∵AB∥CD,FM∥AE,
∴∠CFM=∠DCF,∠AFM=∠FAB=25°,
∵∠ACD=130°,CE平分∠ACD
∴∠DCF=65°,
∴∠CFM=65°,
∴∠AFC=∠CFM+∠AFM=90°
(3)解:当点F在线段CE上时,过点F作FM∥AB,交AC于点M,连接AF,
∴FM∥CD,
∴∠FCD=∠MFC,
∵FM∥AB,
∴∠FAB=∠MFA,
∴∠FCD+∠FAB=∠MFC+∠MFA,
∴∠AFC=∠FCD+∠FAB.
当点F在线段CE的延长线上时,过点F作MF∥AB,连接AF,
∴FM∥CD,
∴∠FCD=∠MFC,
∵FM∥AB,
∴∠FAB=∠MFA,
∵∠MFC=∠MFA+∠AFC,
∴∠FCD=∠FAB+∠AFC.
综上,∠AFC=∠FCD+∠FAB或∠FCD=∠FAB+∠AFC.
【知识点】平行线的性质;角平分线的定义
18.【答案】(1)解:A′B′C′如图所示
(2)解:A′(﹣1,﹣2),B′(2,﹣2),C′(1,0)
(3)解:S△ABC= ×3×2=3
【知识点】作图﹣平移
19.【答案】(1)∠EPF=∠AEP+∠PFC;∠AEP+∠EPF+∠PFC=360°
(2)150°
【知识点】角的运算;平行线的判定与性质;角平分线的定义
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
