第五章三角函数检测卷2023-2024学年高中数学人教A版必修第一册(含解析)
文档属性
| 名称 | 第五章三角函数检测卷2023-2024学年高中数学人教A版必修第一册(含解析) | 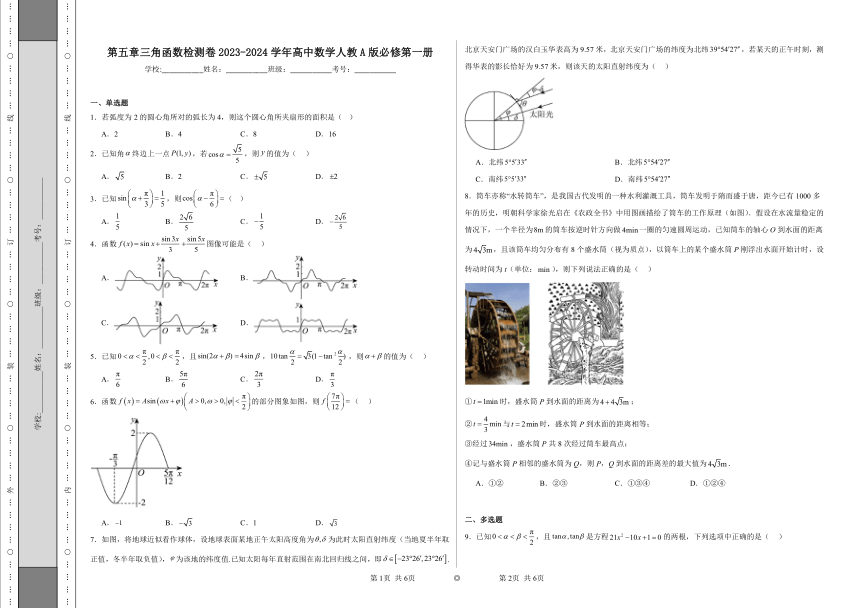 | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-23 13:27:26 | ||
图片预览





文档简介
第五章三角函数检测卷2023-2024学年高中数学人教A版必修第一册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若弧度为2的圆心角所对的弧长为4,则这个圆心角所夹扇形的面积是( )
A.2 B.4 C.8 D.16
2.已知角终边上一点,若,则的值为( )
A. B.2 C. D.
3.已知,则( )
A. B. C. D.
4.函数图像可能是( )
A. B.
C. D.
5.已知,且,,则的值为( )
A. B. C. D.
6.函数的部分图象如图,则( )
A. B. C.1 D.
7.如图,将地球近似看作球体,设地球表面某地正午太阳高度角为为此时太阳直射纬度(当地夏半年取正值,冬半年取负值),为该地的纬度值.已知太阳每年直射范围在南北回归线之间,即.北京天安门广场的汉白玉华表高为9.57米,北京天安门广场的纬度为北纬,若某天的正午时刻,测得华表的影长恰好为9.57米,则该天的太阳直射纬度为( )
A.北纬 B.北纬
C.南纬 D.南纬
8.筒车亦称“水转筒车”,是我国古代发明的一种水利灌溉工具,筒车发明于隋而盛于唐,距今已有1000多年的历史,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图).假设在水流量稳定的情况下,一个半径为的筒车按逆时针方向做一圈的匀速圆周运动,已知筒车的轴心O到水面的距离为,且该筒车均匀分布有8个盛水筒(视为质点),以筒车上的某个盛水筒P刚浮出水面开始计时,设转动时间为t(单位:),则下列说法正确的是( )
①时,盛水筒P到水面的距离为;
②与时,盛水筒P到水面的距离相等;
③经过,盛水筒P共8次经过筒车最高点;
④记与盛水筒P相邻的盛水筒为Q,则P,Q到水面的距离差的最大值为.
A.①② B.②③ C.①③④ D.①②④
二、多选题
9.已知,且是方程的两根,下列选项中正确的是( )
A. B.
C. D.
10.已知函数 ,则( )
A.
B.在定义域上单调递增
C.
D.不等式 f(x)≥1的解集为
11.计算下列各式,结果为的是( )
A.
B.
C.
D.
三、填空题
12.在中,若,,则 .
13.已知函数的部分图像如图所示,则 , .
14.声音是由于物体的振动产生的能引起听觉的波,我们听到的声音多为复合音.若一个复合音的数学模型是函数,则下列结论错误的序号是 ;
①的一个周期为; ②的最大值为;
③的图象关于直线对称; ④在区间上有3个零点.
四、解答题
15.已知函数.
(1)求的最小正周期和对称轴;
(2)若,求的值域.
16.已知
(1)化简;
(2)已知,求的值.
17.已知函数在区间上单调,其中为正整数,,且.
(1)求图象的一条对称轴;
(2)若,求的值.
18.如图,学校新校区有两块空闲的扇形绿化草地(圆心角为)和(圆心角为),为圆的直径.在劣弧和劣弧上分别取点和点,且为圆的直径,分别设计出两块社团活动区域,其中一块为矩形区域,另一块为矩形区域,已知圆的直径米,点在上、点在上、点和在上、点在上.
(1)经设计,当达到最小值时,取得最佳观赏效果.请给出最佳观赏效果的设计方案
(2)学校本周将在矩形区域进行社团活动展示,现需要在矩形区域内铺满地垫,并在矩形区域四周放置围栏.铺设的地垫每平方米20元,围栏每米10元,则场地布置的费用最高不超过多少元
(参考数据:)
19.对于分别定义在,上的函数,以及实数,若任取,存在,使得,则称函数与具有关系.其中称为的像.
(1)若,;,,判断与是否具有关系,并说明理由;
(2)若,;,,且与具有关系,求的像;
(3)若,;,,且与具有关系,求实数的取值范围.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据题意,结合扇形的弧长公式和面积公式,即可求解.
【详解】设扇形所在圆的半径为,
根据题意,可得α=2,l=4,所以,
所以.
故选:B.
2.D
【分析】利用余弦函数的定义列式计算即得.
【详解】由角终边上一点,得,因此,解得,
所以的值为.
故选:D
3.A
【分析】由利用诱导公式计算可得.
【详解】因为,
所以.
故选:A
4.D
【分析】根据函数图象的对称性排除AC,再结合函数值大小排除B,从而得正确结论.
【详解】从四个选项中可以看出,函数的周期性、奇偶性、函数值的正负无法排除任一个选项,
但是,因此的图象关于直线对称,可排除AC,
又,排除B,
故选:D.
5.A
【分析】将转化为,然后由两角和与差的正弦公式展开化简,由,利用二倍角公式化简最后求解即可.
【详解】因为,所以,
所以,
化简得:,
所以,
又由,可得,
所以,即,所以,
所以,又,所以,
所以.
故选:A
6.B
【分析】由图可知,分别求出后,由,得,结合的范围求出,最后得到函数表达式即可求解.
【详解】由图可知,解得,
又,所以,解得,
注意到,从而,
所以,所以.
故选:B.
7.C
【分析】首先根据题意理解太阳高度角、该地纬度、太阳直射纬度的概念,然后由太阳高度角可得结果.
【详解】由题可知,天安门广场的太阳高度角,
由华表的高和影长相等可知,所以.
所以该天太阳直射纬度为南纬
故选:C
8.A
【分析】建立直角坐标系,依题意作图,分析其中的几何关系判断①②,利用周期判断③,求出距离差的表达式结合三角变换求最值判断④即可.
【详解】依题意作图如下:
以水车的轴心为原点建立直角坐标系如图,由题可知水车旋转一周的时间为4min,
当刚露出水面时,与轴的夹角是,相邻盛水桶之间的夹角是,
当旋转时,旋转了,旋转到点,
此时点到水面的距离为,所以①正确;
②当时,旋转了周,即,此时的位置是点,
与轴正半轴的夹角是,
当时,旋转了,即点,与轴正半轴的夹角也是,
点与点到水面的距离相等,所以②正确;
③经过,则水车转过了个周期,所以盛水桶共9次经过最高点,故③错误;
④设在的上方,与轴负方向的夹角为,,
则与轴负方向的夹角为,
相邻两筒到水面的距离差为:
,
其中,,
当时取最大值为,故④错误;
故选:A.
9.AD
【分析】由方程解出,利用两角和与差的正弦余弦正切公式和同角三角函数的商数关系,求解各选项中的算式,验证选项.
【详解】是方程的两根,又,
解得,
,A选项正确;
,B选项错误;
,C选项错误;
,,则,有,
,
,D选项正确.
故选:AD.
10.AC
【分析】对A,直接代入计算即可比较大小;对B,根据正切型函数定义得到不等式,解出即可;对C,直接代入验证判断对称性;对D,根据正切型函数性质列出不等式,解出即可.
【详解】对于A,因为,所以,故A正确;
对于B,由,,得,
故函数的定义域为,因为,故B错误;
对于C,因为,所以点是函数图象的一个对称中心,则,故C正确;
对于D,,即,则,,
解得,所以不等式的解集为,故D错误.
故选:AC.
11.AC
【分析】由两角和与差的正弦,正切公式,二倍角的余弦公式对选项一一判断即可得出答案.
【详解】对于A,
,故A正确;
对于B,因为,
可得,
所以,故B错误;
对于C,,故C正确;
对于D,,故D错误.
故选:AC.
12.
【分析】利用三角形的内角范围与同角三角函数的平方关系,结合诱导公式与两角和的正弦公式即可求解.
【详解】因为在中,,
又,,
所以, ,
又,所以,
所以
.
故答案为:.
13. 2 /
【分析】由图象首先得,然后由点对应的正弦函数上的点求出,再由图象确定周期,得值.
【详解】由图形,
,,由图象知,而,所以,
由图象知最小正周期为,所以,
故答案为:2;.
14.①②③
【分析】对于①,代入周期的定义,即可判断;对于②,分别比较两个函数取得最大值的值,即可判断;对于③,代入对称性的公式,即可求解;对于④,根据零点的定义,解方程,即可判断.
【详解】对于①,,故①错误;
对于②,,当,时,取得最大值1,,
当,时,即,时,取得最大值,
所以两个函数不可能同时取得最大值,所以的最大值不是,故②错误;
对于③,,
所以函数的图象不关于直线对称,故③错误;
对于④,,
即,,
即或,解得:或或,
所以函数在区间上有3个零点,故④正确.
故答案为:①②③.
15.(1)最小正周期为,;
(2).
【分析】(1)利用余弦函数的周期公式、整体代入法计算对称轴即可;
(2)利用余弦函数的性质计算值域即可.
【详解】(1)最小正周期为,
令可得:,
所以的对称轴为.
(2)由可知,
由余弦函数的性质可知,,
即的值域为
16.(1)
(2)
【分析】(1)根据诱导公式直接化简;
(2)为待求表达式补上分母,然后分子分母同时除以即可.
【详解】(1)依题意得,
(2)依题意得,,所以,
于是
17.(1)
(2)
【分析】(1)由函数在区间上的单调性,根据题意和最小正周期的定义,求得,再结合,即可确定对称轴;
(2)根据函数对称轴及函数值确定的表达式,再结合最小正周期确定的可能取值,分类讨论,即可求解.
【详解】(1)解:因为函数在区间上单调,
所以函数的最小正周期,
又因为,所以,
即直线为图象的一条对称轴.
(2)解:由(1)最小正周期,可得,
因为,所以或或,
又因为为图象的一条对称轴,可得,
因为,可得或,
若,则,
即,
此时不存在整数,使得或或;
若,则,
即,
此时不存在整数,使得或,
当时,可得,此时,
因为,所以.
18.(1)答案见解析
(2)元
【分析】(1)设,设,则且,利用辅助角公式得到,即可求出的最小值,从而求出,即可得解;
(2)依题意可得,即可表示矩形的面积、周长,所以场地布置的费用,利用换元法求出,即可得解.
【详解】(1)设,
由得,,
设,则且,
即,其中,
由得,即或(舍去),
即的最小值为,此时,
又,解得,
所以当时,达到最小值时,取得最佳观赏效果,
即当时达到最小值时,取得最佳观赏效果.
(2)在矩形中,,
所以矩形的面积为,周长为,
所以场地布置的费用
,
令,则,
又,因为,所以,
所以,所以,
则,
又在上单调递增,
当时,元,
即当时场地布置的费用最高为元,所以场地布置的费用最高不超过元.
19.(1)不具有,理由见解析;
(2)或或;
(3)或,
【分析】(1)根据具有关系的定义及三角函数的值域判断即可;
(2)根据具有关系及三角函数的性质计算即可;
(3)利用三角函数的性质先确定,根据具有关系的定义得出,再根据二次函数的动轴定区间分类讨论计算即可.
【详解】(1)与不具有关系,
理由如下:时,,,所以,
则与不具有关系;
(2)由题意可知
,
所以,
又,所以,
解之得或或,
即的像为或或;
(3)对于,则,所以,
即,
因为与具有关系,
所以要满足题意需,使得即可.
令,
令,则,设,
①若,即时,,
则,
②若,即时,,
则,
③若,即时,,
则或,显然无解,
④若,即时,,
则或,显然无解,
综上所述:或,
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若弧度为2的圆心角所对的弧长为4,则这个圆心角所夹扇形的面积是( )
A.2 B.4 C.8 D.16
2.已知角终边上一点,若,则的值为( )
A. B.2 C. D.
3.已知,则( )
A. B. C. D.
4.函数图像可能是( )
A. B.
C. D.
5.已知,且,,则的值为( )
A. B. C. D.
6.函数的部分图象如图,则( )
A. B. C.1 D.
7.如图,将地球近似看作球体,设地球表面某地正午太阳高度角为为此时太阳直射纬度(当地夏半年取正值,冬半年取负值),为该地的纬度值.已知太阳每年直射范围在南北回归线之间,即.北京天安门广场的汉白玉华表高为9.57米,北京天安门广场的纬度为北纬,若某天的正午时刻,测得华表的影长恰好为9.57米,则该天的太阳直射纬度为( )
A.北纬 B.北纬
C.南纬 D.南纬
8.筒车亦称“水转筒车”,是我国古代发明的一种水利灌溉工具,筒车发明于隋而盛于唐,距今已有1000多年的历史,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图).假设在水流量稳定的情况下,一个半径为的筒车按逆时针方向做一圈的匀速圆周运动,已知筒车的轴心O到水面的距离为,且该筒车均匀分布有8个盛水筒(视为质点),以筒车上的某个盛水筒P刚浮出水面开始计时,设转动时间为t(单位:),则下列说法正确的是( )
①时,盛水筒P到水面的距离为;
②与时,盛水筒P到水面的距离相等;
③经过,盛水筒P共8次经过筒车最高点;
④记与盛水筒P相邻的盛水筒为Q,则P,Q到水面的距离差的最大值为.
A.①② B.②③ C.①③④ D.①②④
二、多选题
9.已知,且是方程的两根,下列选项中正确的是( )
A. B.
C. D.
10.已知函数 ,则( )
A.
B.在定义域上单调递增
C.
D.不等式 f(x)≥1的解集为
11.计算下列各式,结果为的是( )
A.
B.
C.
D.
三、填空题
12.在中,若,,则 .
13.已知函数的部分图像如图所示,则 , .
14.声音是由于物体的振动产生的能引起听觉的波,我们听到的声音多为复合音.若一个复合音的数学模型是函数,则下列结论错误的序号是 ;
①的一个周期为; ②的最大值为;
③的图象关于直线对称; ④在区间上有3个零点.
四、解答题
15.已知函数.
(1)求的最小正周期和对称轴;
(2)若,求的值域.
16.已知
(1)化简;
(2)已知,求的值.
17.已知函数在区间上单调,其中为正整数,,且.
(1)求图象的一条对称轴;
(2)若,求的值.
18.如图,学校新校区有两块空闲的扇形绿化草地(圆心角为)和(圆心角为),为圆的直径.在劣弧和劣弧上分别取点和点,且为圆的直径,分别设计出两块社团活动区域,其中一块为矩形区域,另一块为矩形区域,已知圆的直径米,点在上、点在上、点和在上、点在上.
(1)经设计,当达到最小值时,取得最佳观赏效果.请给出最佳观赏效果的设计方案
(2)学校本周将在矩形区域进行社团活动展示,现需要在矩形区域内铺满地垫,并在矩形区域四周放置围栏.铺设的地垫每平方米20元,围栏每米10元,则场地布置的费用最高不超过多少元
(参考数据:)
19.对于分别定义在,上的函数,以及实数,若任取,存在,使得,则称函数与具有关系.其中称为的像.
(1)若,;,,判断与是否具有关系,并说明理由;
(2)若,;,,且与具有关系,求的像;
(3)若,;,,且与具有关系,求实数的取值范围.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据题意,结合扇形的弧长公式和面积公式,即可求解.
【详解】设扇形所在圆的半径为,
根据题意,可得α=2,l=4,所以,
所以.
故选:B.
2.D
【分析】利用余弦函数的定义列式计算即得.
【详解】由角终边上一点,得,因此,解得,
所以的值为.
故选:D
3.A
【分析】由利用诱导公式计算可得.
【详解】因为,
所以.
故选:A
4.D
【分析】根据函数图象的对称性排除AC,再结合函数值大小排除B,从而得正确结论.
【详解】从四个选项中可以看出,函数的周期性、奇偶性、函数值的正负无法排除任一个选项,
但是,因此的图象关于直线对称,可排除AC,
又,排除B,
故选:D.
5.A
【分析】将转化为,然后由两角和与差的正弦公式展开化简,由,利用二倍角公式化简最后求解即可.
【详解】因为,所以,
所以,
化简得:,
所以,
又由,可得,
所以,即,所以,
所以,又,所以,
所以.
故选:A
6.B
【分析】由图可知,分别求出后,由,得,结合的范围求出,最后得到函数表达式即可求解.
【详解】由图可知,解得,
又,所以,解得,
注意到,从而,
所以,所以.
故选:B.
7.C
【分析】首先根据题意理解太阳高度角、该地纬度、太阳直射纬度的概念,然后由太阳高度角可得结果.
【详解】由题可知,天安门广场的太阳高度角,
由华表的高和影长相等可知,所以.
所以该天太阳直射纬度为南纬
故选:C
8.A
【分析】建立直角坐标系,依题意作图,分析其中的几何关系判断①②,利用周期判断③,求出距离差的表达式结合三角变换求最值判断④即可.
【详解】依题意作图如下:
以水车的轴心为原点建立直角坐标系如图,由题可知水车旋转一周的时间为4min,
当刚露出水面时,与轴的夹角是,相邻盛水桶之间的夹角是,
当旋转时,旋转了,旋转到点,
此时点到水面的距离为,所以①正确;
②当时,旋转了周,即,此时的位置是点,
与轴正半轴的夹角是,
当时,旋转了,即点,与轴正半轴的夹角也是,
点与点到水面的距离相等,所以②正确;
③经过,则水车转过了个周期,所以盛水桶共9次经过最高点,故③错误;
④设在的上方,与轴负方向的夹角为,,
则与轴负方向的夹角为,
相邻两筒到水面的距离差为:
,
其中,,
当时取最大值为,故④错误;
故选:A.
9.AD
【分析】由方程解出,利用两角和与差的正弦余弦正切公式和同角三角函数的商数关系,求解各选项中的算式,验证选项.
【详解】是方程的两根,又,
解得,
,A选项正确;
,B选项错误;
,C选项错误;
,,则,有,
,
,D选项正确.
故选:AD.
10.AC
【分析】对A,直接代入计算即可比较大小;对B,根据正切型函数定义得到不等式,解出即可;对C,直接代入验证判断对称性;对D,根据正切型函数性质列出不等式,解出即可.
【详解】对于A,因为,所以,故A正确;
对于B,由,,得,
故函数的定义域为,因为,故B错误;
对于C,因为,所以点是函数图象的一个对称中心,则,故C正确;
对于D,,即,则,,
解得,所以不等式的解集为,故D错误.
故选:AC.
11.AC
【分析】由两角和与差的正弦,正切公式,二倍角的余弦公式对选项一一判断即可得出答案.
【详解】对于A,
,故A正确;
对于B,因为,
可得,
所以,故B错误;
对于C,,故C正确;
对于D,,故D错误.
故选:AC.
12.
【分析】利用三角形的内角范围与同角三角函数的平方关系,结合诱导公式与两角和的正弦公式即可求解.
【详解】因为在中,,
又,,
所以, ,
又,所以,
所以
.
故答案为:.
13. 2 /
【分析】由图象首先得,然后由点对应的正弦函数上的点求出,再由图象确定周期,得值.
【详解】由图形,
,,由图象知,而,所以,
由图象知最小正周期为,所以,
故答案为:2;.
14.①②③
【分析】对于①,代入周期的定义,即可判断;对于②,分别比较两个函数取得最大值的值,即可判断;对于③,代入对称性的公式,即可求解;对于④,根据零点的定义,解方程,即可判断.
【详解】对于①,,故①错误;
对于②,,当,时,取得最大值1,,
当,时,即,时,取得最大值,
所以两个函数不可能同时取得最大值,所以的最大值不是,故②错误;
对于③,,
所以函数的图象不关于直线对称,故③错误;
对于④,,
即,,
即或,解得:或或,
所以函数在区间上有3个零点,故④正确.
故答案为:①②③.
15.(1)最小正周期为,;
(2).
【分析】(1)利用余弦函数的周期公式、整体代入法计算对称轴即可;
(2)利用余弦函数的性质计算值域即可.
【详解】(1)最小正周期为,
令可得:,
所以的对称轴为.
(2)由可知,
由余弦函数的性质可知,,
即的值域为
16.(1)
(2)
【分析】(1)根据诱导公式直接化简;
(2)为待求表达式补上分母,然后分子分母同时除以即可.
【详解】(1)依题意得,
(2)依题意得,,所以,
于是
17.(1)
(2)
【分析】(1)由函数在区间上的单调性,根据题意和最小正周期的定义,求得,再结合,即可确定对称轴;
(2)根据函数对称轴及函数值确定的表达式,再结合最小正周期确定的可能取值,分类讨论,即可求解.
【详解】(1)解:因为函数在区间上单调,
所以函数的最小正周期,
又因为,所以,
即直线为图象的一条对称轴.
(2)解:由(1)最小正周期,可得,
因为,所以或或,
又因为为图象的一条对称轴,可得,
因为,可得或,
若,则,
即,
此时不存在整数,使得或或;
若,则,
即,
此时不存在整数,使得或,
当时,可得,此时,
因为,所以.
18.(1)答案见解析
(2)元
【分析】(1)设,设,则且,利用辅助角公式得到,即可求出的最小值,从而求出,即可得解;
(2)依题意可得,即可表示矩形的面积、周长,所以场地布置的费用,利用换元法求出,即可得解.
【详解】(1)设,
由得,,
设,则且,
即,其中,
由得,即或(舍去),
即的最小值为,此时,
又,解得,
所以当时,达到最小值时,取得最佳观赏效果,
即当时达到最小值时,取得最佳观赏效果.
(2)在矩形中,,
所以矩形的面积为,周长为,
所以场地布置的费用
,
令,则,
又,因为,所以,
所以,所以,
则,
又在上单调递增,
当时,元,
即当时场地布置的费用最高为元,所以场地布置的费用最高不超过元.
19.(1)不具有,理由见解析;
(2)或或;
(3)或,
【分析】(1)根据具有关系的定义及三角函数的值域判断即可;
(2)根据具有关系及三角函数的性质计算即可;
(3)利用三角函数的性质先确定,根据具有关系的定义得出,再根据二次函数的动轴定区间分类讨论计算即可.
【详解】(1)与不具有关系,
理由如下:时,,,所以,
则与不具有关系;
(2)由题意可知
,
所以,
又,所以,
解之得或或,
即的像为或或;
(3)对于,则,所以,
即,
因为与具有关系,
所以要满足题意需,使得即可.
令,
令,则,设,
①若,即时,,
则,
②若,即时,,
则,
③若,即时,,
则或,显然无解,
④若,即时,,
则或,显然无解,
综上所述:或,
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
