鲁教版九年级数学下册第五单元5.6直线和圆的位置关系同步辅导(含答案)
文档属性
| 名称 | 鲁教版九年级数学下册第五单元5.6直线和圆的位置关系同步辅导(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 121.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-30 20:57:25 | ||
图片预览

文档简介
5.6直线和圆的位置关系同步辅导(含答案)
一、知识梳理:
1、直线与圆的位置关系:
直线和圆相交时,d r;直线和圆相且时,d r;直线和圆相离时,d r。
2、切线的性质:圆的切线垂直于 。
3、切线的判定:过 这条半径的直线是圆的切线。
4、内心:是 交点,到 的距离相等。
5、切线长定理: 。
6、Rt△ABC的三边是a,b,c则其内切圆的半径是 ;外接圆的半径是 。
二、典例精析
1、已知⊙O的直径是16cm,点O到同一平面内直线l的距离为9cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
2、已知⊙O半径为3,M为直线AB上一点,若MO=3,则直线AB与⊙O的位置关系为( )
A.相切 B.相交 C.相切或相离 D.相切或相交
3、如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )
A.2.3 B.2.4 C.2.5 D.2.6
(3题图) (4题图) (5题图) (6题图)
4、如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
A.40° B.55° C.65° D.70°
5、如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.
(1)求∠DOA的度数;
(2)求证:直线ED与⊙O相切.
6、如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD的周长等于10cm,则PA= cm.
三、对应练习
7、⊙O的半径为6,一条弦长,以3为半径的同心圆与这条弦的关系是( )
A.相切 B.相交 C.相离 D.相切或相交
8、已知⊙O的半径为5,直线l上有一点P满足PO=5,则直线l与⊙O的位置关系是( )
A.相切 B.相离 C.相离或相切 D.相切或相交
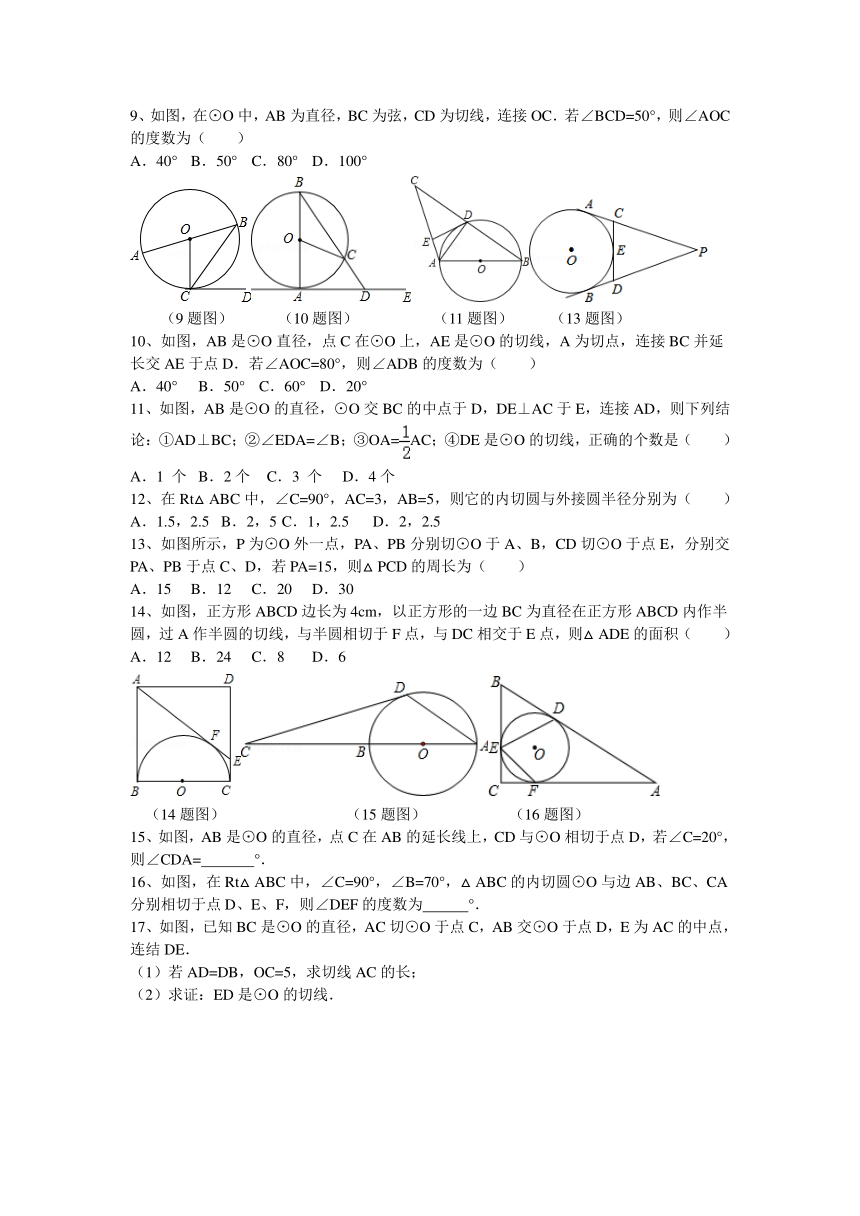
9、如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
A.40° B.50° C.80° D.100°
(9题图) (10题图) (11题图) (13题图)
10、如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
A.40° B.50° C.60° D.20°
11、如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线,正确的个数是( )
A.1 个 B.2个 C.3 个 D.4个
12、在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B.2,5 C.1,2.5 D.2,2.5
13、如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( )
A.15 B.12 C.20 D.30
14、如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12 B.24 C.8 D.6
(14题图) (15题图) (16题图)
15、如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA= °.
16、如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为 °.
17、如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE.
(1)若AD=DB,OC=5,求切线AC的长;
(2)求证:ED是⊙O的切线.
18、如图,已知R t△ABC,∠ABC=90°,以直角边AB为直径作O,交斜边AC于点D,连接BD.
(1)取BC的中点E,连接ED,试证明ED与⊙O相切.
(2)若AD=3,BD=4,求边BC的长.
19、如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE
(1)求证:△ABC∽△CBD;
(2)求证:直线DE是⊙O的切线.
20、如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.
(1)判断DE与⊙O的位置关系并说明理由;
(2)若AC=16,tanA=,求⊙O的半径.
参考答案
1、C.2、D.3、B.4、B.
5、(1)解;∵∠DBA=50°,∴∠DOA=2∠DBA=100°,
(2)证明:连接OE.在△EAO与△EDO中,,∴△EAO≌△EDO,
∴∠EDO=∠EAO,
∵∠BAC=90°,∴∠EDO=90°,∴DE与⊙O相切.
6、5 7、A. 8、D. 9、C. 10、B. 11、D. 12、C. 13、D.
14、D.15、125 16、80
17、(1)解:连接CD,
∵BC是⊙O的直径,∴∠BDC=90°,即CD⊥AB,
∵AD=DB,OC=5,∴CD是AB的垂直平分线,∴AC=BC=2OC=10;
(2)证明:连接OD,如图所示,
∵∠ADC=90°,E为AC的中点,∴DE=EC=AC,∴∠1=∠2,
∵OD=OC,∴∠3=∠4,
∵AC切⊙O于点C,∴AC⊥OC,∴∠1+∠3=∠2+∠4=90°,即DE⊥OD,
∴ED是⊙O的切线.
18、(1)证明:连接OD.
∵OD=OB,∴∠OBD=∠BDO;
∵AB是直径(已知),∴∠ADB=90°,∴∠ADB=∠BDC=90°;
在Rt△BDC中,E是BC的中点,∴BE=CE=DE,∴∠DBE=∠BDE;
又∵∠ABC=∠OBD+∠DBE=90°,∴∠ODE=∠BDO+∠BDE=90°;
∵点D在⊙O上,∴ED与⊙O相切;
(2)在Rt△ABD中,∵AD=3,BD=4,∴AB=5(勾股定理);
在Rt△BDC和Rt△ADB中,∠ADB=∠BDC=90°,∠ABC=90°,
∴∠ABD+∠DBC=90°,∠BCD+∠DBC=90°,∴∠ABD=∠BCD,∴△BDC∽△ADB,
∴=.即=,∴BC=.
(18题图) (19题图) (20题图)
19、(1)证明:∵AC为⊙O的直径,∴∠ADC=90°,∴∠BDC=90°,
又∵∠ACB=90°,∴∠ACB=∠BDC,又∵∠B=∠B,∴△BCD∽△BAC;
(2)连结DO,如图,
∵∠BDC=90°,E为BC的中点,∴DE=CE=BE,∴∠EDC=∠ECD,
又∵OD=OC,∴∠ODC=∠OCD,而∠OCD+∠DCE=∠ACB=90°,
∴∠EDC+∠ODC=90°,即∠EDO=90°,
∴DE⊥OD,∴DE与⊙O相切.
20、解:(1)DE与⊙O相切.理由如下:
连接DO,BD,如图,
∵∠BDE=∠A,∠A=∠ADO,∴∠ADO=∠EDB,
∵AB为⊙O的直径,∴∠ADB=90°,∴∠ADO+∠ODB=90°,
∴∠ODB+∠EDB=90°,即∠ODE=90°,
∴OD⊥DE,∴DE为⊙O的切线;
(2)∵∠BDE=∠A,∴∠ABD=∠EBD,
而BD⊥AC,∴△ABC为等腰三角形,∴AD=CD=AC=8,
在Rt△ABD中,∵tanA==,∴BD=×8=6,∴AB==10,∴⊙O的半径为5.
一、知识梳理:
1、直线与圆的位置关系:
直线和圆相交时,d r;直线和圆相且时,d r;直线和圆相离时,d r。
2、切线的性质:圆的切线垂直于 。
3、切线的判定:过 这条半径的直线是圆的切线。
4、内心:是 交点,到 的距离相等。
5、切线长定理: 。
6、Rt△ABC的三边是a,b,c则其内切圆的半径是 ;外接圆的半径是 。
二、典例精析
1、已知⊙O的直径是16cm,点O到同一平面内直线l的距离为9cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
2、已知⊙O半径为3,M为直线AB上一点,若MO=3,则直线AB与⊙O的位置关系为( )
A.相切 B.相交 C.相切或相离 D.相切或相交
3、如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )
A.2.3 B.2.4 C.2.5 D.2.6
(3题图) (4题图) (5题图) (6题图)
4、如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
A.40° B.55° C.65° D.70°
5、如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.
(1)求∠DOA的度数;
(2)求证:直线ED与⊙O相切.
6、如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD的周长等于10cm,则PA= cm.
三、对应练习
7、⊙O的半径为6,一条弦长,以3为半径的同心圆与这条弦的关系是( )
A.相切 B.相交 C.相离 D.相切或相交
8、已知⊙O的半径为5,直线l上有一点P满足PO=5,则直线l与⊙O的位置关系是( )
A.相切 B.相离 C.相离或相切 D.相切或相交
9、如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
A.40° B.50° C.80° D.100°
(9题图) (10题图) (11题图) (13题图)
10、如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
A.40° B.50° C.60° D.20°
11、如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线,正确的个数是( )
A.1 个 B.2个 C.3 个 D.4个
12、在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B.2,5 C.1,2.5 D.2,2.5
13、如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( )
A.15 B.12 C.20 D.30
14、如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12 B.24 C.8 D.6
(14题图) (15题图) (16题图)
15、如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA= °.
16、如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为 °.
17、如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE.
(1)若AD=DB,OC=5,求切线AC的长;
(2)求证:ED是⊙O的切线.
18、如图,已知R t△ABC,∠ABC=90°,以直角边AB为直径作O,交斜边AC于点D,连接BD.
(1)取BC的中点E,连接ED,试证明ED与⊙O相切.
(2)若AD=3,BD=4,求边BC的长.
19、如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE
(1)求证:△ABC∽△CBD;
(2)求证:直线DE是⊙O的切线.
20、如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.
(1)判断DE与⊙O的位置关系并说明理由;
(2)若AC=16,tanA=,求⊙O的半径.
参考答案
1、C.2、D.3、B.4、B.
5、(1)解;∵∠DBA=50°,∴∠DOA=2∠DBA=100°,
(2)证明:连接OE.在△EAO与△EDO中,,∴△EAO≌△EDO,
∴∠EDO=∠EAO,
∵∠BAC=90°,∴∠EDO=90°,∴DE与⊙O相切.
6、5 7、A. 8、D. 9、C. 10、B. 11、D. 12、C. 13、D.
14、D.15、125 16、80
17、(1)解:连接CD,
∵BC是⊙O的直径,∴∠BDC=90°,即CD⊥AB,
∵AD=DB,OC=5,∴CD是AB的垂直平分线,∴AC=BC=2OC=10;
(2)证明:连接OD,如图所示,
∵∠ADC=90°,E为AC的中点,∴DE=EC=AC,∴∠1=∠2,
∵OD=OC,∴∠3=∠4,
∵AC切⊙O于点C,∴AC⊥OC,∴∠1+∠3=∠2+∠4=90°,即DE⊥OD,
∴ED是⊙O的切线.
18、(1)证明:连接OD.
∵OD=OB,∴∠OBD=∠BDO;
∵AB是直径(已知),∴∠ADB=90°,∴∠ADB=∠BDC=90°;
在Rt△BDC中,E是BC的中点,∴BE=CE=DE,∴∠DBE=∠BDE;
又∵∠ABC=∠OBD+∠DBE=90°,∴∠ODE=∠BDO+∠BDE=90°;
∵点D在⊙O上,∴ED与⊙O相切;
(2)在Rt△ABD中,∵AD=3,BD=4,∴AB=5(勾股定理);
在Rt△BDC和Rt△ADB中,∠ADB=∠BDC=90°,∠ABC=90°,
∴∠ABD+∠DBC=90°,∠BCD+∠DBC=90°,∴∠ABD=∠BCD,∴△BDC∽△ADB,
∴=.即=,∴BC=.
(18题图) (19题图) (20题图)
19、(1)证明:∵AC为⊙O的直径,∴∠ADC=90°,∴∠BDC=90°,
又∵∠ACB=90°,∴∠ACB=∠BDC,又∵∠B=∠B,∴△BCD∽△BAC;
(2)连结DO,如图,
∵∠BDC=90°,E为BC的中点,∴DE=CE=BE,∴∠EDC=∠ECD,
又∵OD=OC,∴∠ODC=∠OCD,而∠OCD+∠DCE=∠ACB=90°,
∴∠EDC+∠ODC=90°,即∠EDO=90°,
∴DE⊥OD,∴DE与⊙O相切.
20、解:(1)DE与⊙O相切.理由如下:
连接DO,BD,如图,
∵∠BDE=∠A,∠A=∠ADO,∴∠ADO=∠EDB,
∵AB为⊙O的直径,∴∠ADB=90°,∴∠ADO+∠ODB=90°,
∴∠ODB+∠EDB=90°,即∠ODE=90°,
∴OD⊥DE,∴DE为⊙O的切线;
(2)∵∠BDE=∠A,∴∠ABD=∠EBD,
而BD⊥AC,∴△ABC为等腰三角形,∴AD=CD=AC=8,
在Rt△ABD中,∵tanA==,∴BD=×8=6,∴AB==10,∴⊙O的半径为5.
