鲁教版九年级数学下册第五单元5.8正多边形和圆(含答案)
文档属性
| 名称 | 鲁教版九年级数学下册第五单元5.8正多边形和圆(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 126.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-22 08:13:31 | ||
图片预览


文档简介
鲁教版九年级数学下册第五单元5.7正多边形和圆(含答案)
一、知识梳理
1、一个正n边形有 条对称轴,这些对称轴交于一点,它到各 的距离都相等,到 的距离也相等,这个点叫做正多边形的 。
2、中心角的度数是 。
3、正n边形的n条半径把正n边形分成n个全等的 ,边心距又把它分成全等的 。
二、典例精析
1、已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
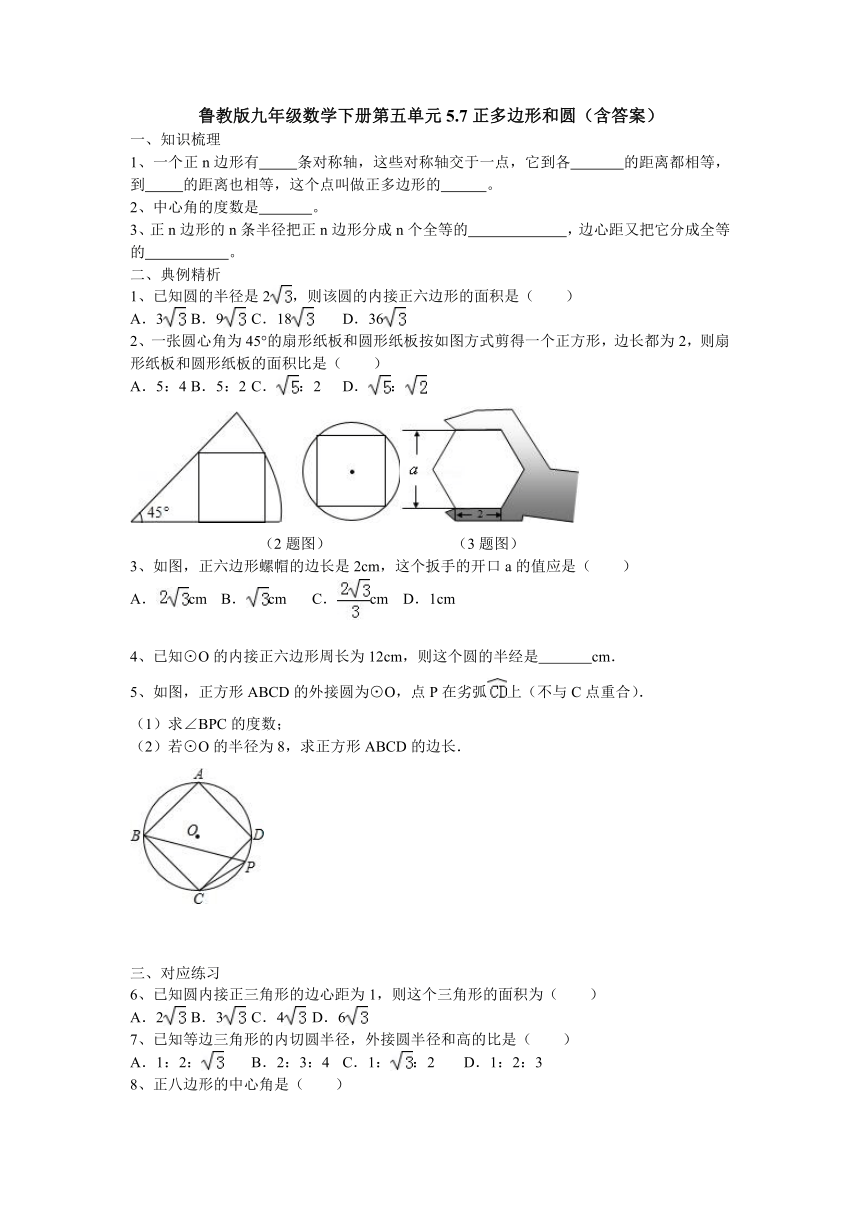
2、一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为2,则扇形纸板和圆形纸板的面积比是( )
A.5:4 B.5:2 C.:2 D.:
(2题图) (3题图)
3、如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )
A.cm B.cm C.cm D.1cm
4、已知⊙O的内接正六边形周长为12cm,则这个圆的半经是 cm.
5、如图,正方形ABCD的外接圆为⊙O,点P在劣弧上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
三、对应练习
6、已知圆内接正三角形的边心距为1,则这个三角形的面积为( )
A.2 B.3 C.4 D.6
7、已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2: B.2:3:4 C.1::2 D.1:2:3
8、正八边形的中心角是( )
A.45° B.135° C.360° D.1080°
9、若六边形的边心距为,则这个正六边形的半径为( )
A.1 B.2 C.4 D.
10、如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于 .
(10题图) (11题图) (12题图)
11、如图,正三角形ABC内接于⊙O,若AB=cm,求⊙O的半径.
12、(1)O是正△ABC的 ,它是△ABC的 圆与 圆的圆心.
(2)OB叫正△ABC的 ,它是正△ABC的 圆的半径.
(3)OD叫作正△ABC ,它是正△ABC的 圆的半径.
(4)∠BOC是正△ABC的 角;∠BOC= 度;∠BOD= 度.
13、如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形;
(2)已知△ABC的边长为4cm,求⊙O的半径.
14、如图,PA、PB、CD是⊙O的切线,切点分别为点A、B、E,若△PCD的周长为18cm,∠APB=60°,求⊙O的半径.
15、如图,已知AB是⊙O的直径,弦AC平分∠DAB,过点C作直线CD,使得CD⊥AD于D.
(1)求证:直线CD与⊙O相切;
(2)若AD=3,AC=,求直径AB的长.
16、如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于E.
(1)求证:BC是⊙O的切线.
(2)当△ABC满足什么条件时,以点O、B、E、D为顶点的四边形是正方形?
参考答案
1、C.2、A.3、A.4、2
5、解:(1)连接OB,OC,
∵四边形ABCD为正方形,∴∠BOC=90°,∴∠P=∠BOC=45°;
(2)过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,∴∠OBE=45°,∴OE=BE,
∵OE2+BE2=OB2,∴BE===4∴BC=2BE=2×4=8.
(5题图) (11题图) (13题图)
6、B.7、D.8、A.9、C.10、2π
11、解:过点O作OD⊥BC于点D,连接BO,
∵正三角形ABC内接于⊙O,∴点O即是三角形内心也是外心,
∴∠OBD=30°,BD=CD=BC=AB=,∴cos30°===,解得:BO=2,
即⊙O的半径为2cm.
12、中心 外接 内切 半径 外接 边心距 内切 中心角 120 60
13、(1)证明:∵∠APC=∠ABC,∠CPB=∠BAC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°.
∴∠ABC=∠BAC=∠ACB=60°.
∴△ABC是等边三角形.
(2)解:连接AO并延长其交BC于D,那么AD⊥BC,连接OB.
∵AD⊥BC,AB=AC∴∠BAD=∠BAC=30°
∴在直角三角形ABD中,AB=4,BD=2
根据勾股定理AD=2.
直角三角形OBD中,OD=AD﹣OA=AD﹣OB=2﹣OB,BD=2,
根据勾股定理可得:OB2=BD2+OD2
即OB2=(2﹣OB)2+4.解得:OB=.因此⊙O的半径是cm.
14、解:连接OA,OP,则OA⊥PA,
根据题意可得:CA=CE,DE=DB,PA=PB,
∵PC+CE=DE+PD=18,
∴PC+CA+DB+PD=18,
∴PA=×18=9(cm),
∵PA、PB是⊙O的切线,
∴∠APO=∠APB=30°,
在Rt△AOP中,PO=2AO,AO>0,
故OA2+92=(2AO)2,
解得:OA=2,
故⊙O的半径为:3cm.
(14题图) (15题图) (16题图)
15、(1)证明:连接OC
∵OA=OC∴∠OAC=∠OCA
∵AC平分∠DAB∴∠DAC=∠OAC∴∠DAC=∠OCA,∴OC∥AD
∵AD⊥CD,∴OC⊥CD.又∵OC是⊙O的半径,∴直线CD与⊙O相切于点C
(2)解:连接BC,则∠ACB=90°.
∵∠DAC=∠OAC,∠ADC=∠ACB=90°,∴△ADC∽△ACB,
∴,∴.
16、解:(1)连接OD、OE,
∵O为AB的中点,E为BC的中点,∴OE为△ABC的中位线,
∴OE∥AC,∴∠DOE=∠ODA,∠BOE=∠A,
∵OA=OD∴∠A=∠ODA,∴∠DOE=∠BOE
∵OD=OB,OE=OE,∴△ODE≌△OBE,∴∠ODE=∠OBE
∵DE是⊙O的切线,∴∠ODE=∠OBE=90°
∴OB⊥BC,∴BC是⊙O的切线.
(2)当为等腰三角形(AB=BC)时四边形OBDE是正方形,证明如下:
连接BD,
∵AB是⊙O的直径,∴BD⊥AC,
∵AB=BC,∴D为AC的中点,
∵E为BC的中点,∴DE为△ABC的中位线,∴DE∥AB,
∵DE为⊙O的切线,∴OD⊥DE,∴OD⊥AB,∴∠DOB=∠OBE=∠ODE=90°,
∵OD=OB,∴四边形OBED为正方形.
一、知识梳理
1、一个正n边形有 条对称轴,这些对称轴交于一点,它到各 的距离都相等,到 的距离也相等,这个点叫做正多边形的 。
2、中心角的度数是 。
3、正n边形的n条半径把正n边形分成n个全等的 ,边心距又把它分成全等的 。
二、典例精析
1、已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
2、一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为2,则扇形纸板和圆形纸板的面积比是( )
A.5:4 B.5:2 C.:2 D.:
(2题图) (3题图)
3、如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )
A.cm B.cm C.cm D.1cm
4、已知⊙O的内接正六边形周长为12cm,则这个圆的半经是 cm.
5、如图,正方形ABCD的外接圆为⊙O,点P在劣弧上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
三、对应练习
6、已知圆内接正三角形的边心距为1,则这个三角形的面积为( )
A.2 B.3 C.4 D.6
7、已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2: B.2:3:4 C.1::2 D.1:2:3
8、正八边形的中心角是( )
A.45° B.135° C.360° D.1080°
9、若六边形的边心距为,则这个正六边形的半径为( )
A.1 B.2 C.4 D.
10、如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于 .
(10题图) (11题图) (12题图)
11、如图,正三角形ABC内接于⊙O,若AB=cm,求⊙O的半径.
12、(1)O是正△ABC的 ,它是△ABC的 圆与 圆的圆心.
(2)OB叫正△ABC的 ,它是正△ABC的 圆的半径.
(3)OD叫作正△ABC ,它是正△ABC的 圆的半径.
(4)∠BOC是正△ABC的 角;∠BOC= 度;∠BOD= 度.
13、如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形;
(2)已知△ABC的边长为4cm,求⊙O的半径.
14、如图,PA、PB、CD是⊙O的切线,切点分别为点A、B、E,若△PCD的周长为18cm,∠APB=60°,求⊙O的半径.
15、如图,已知AB是⊙O的直径,弦AC平分∠DAB,过点C作直线CD,使得CD⊥AD于D.
(1)求证:直线CD与⊙O相切;
(2)若AD=3,AC=,求直径AB的长.
16、如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于E.
(1)求证:BC是⊙O的切线.
(2)当△ABC满足什么条件时,以点O、B、E、D为顶点的四边形是正方形?
参考答案
1、C.2、A.3、A.4、2
5、解:(1)连接OB,OC,
∵四边形ABCD为正方形,∴∠BOC=90°,∴∠P=∠BOC=45°;
(2)过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,∴∠OBE=45°,∴OE=BE,
∵OE2+BE2=OB2,∴BE===4∴BC=2BE=2×4=8.
(5题图) (11题图) (13题图)
6、B.7、D.8、A.9、C.10、2π
11、解:过点O作OD⊥BC于点D,连接BO,
∵正三角形ABC内接于⊙O,∴点O即是三角形内心也是外心,
∴∠OBD=30°,BD=CD=BC=AB=,∴cos30°===,解得:BO=2,
即⊙O的半径为2cm.
12、中心 外接 内切 半径 外接 边心距 内切 中心角 120 60
13、(1)证明:∵∠APC=∠ABC,∠CPB=∠BAC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°.
∴∠ABC=∠BAC=∠ACB=60°.
∴△ABC是等边三角形.
(2)解:连接AO并延长其交BC于D,那么AD⊥BC,连接OB.
∵AD⊥BC,AB=AC∴∠BAD=∠BAC=30°
∴在直角三角形ABD中,AB=4,BD=2
根据勾股定理AD=2.
直角三角形OBD中,OD=AD﹣OA=AD﹣OB=2﹣OB,BD=2,
根据勾股定理可得:OB2=BD2+OD2
即OB2=(2﹣OB)2+4.解得:OB=.因此⊙O的半径是cm.
14、解:连接OA,OP,则OA⊥PA,
根据题意可得:CA=CE,DE=DB,PA=PB,
∵PC+CE=DE+PD=18,
∴PC+CA+DB+PD=18,
∴PA=×18=9(cm),
∵PA、PB是⊙O的切线,
∴∠APO=∠APB=30°,
在Rt△AOP中,PO=2AO,AO>0,
故OA2+92=(2AO)2,
解得:OA=2,
故⊙O的半径为:3cm.
(14题图) (15题图) (16题图)
15、(1)证明:连接OC
∵OA=OC∴∠OAC=∠OCA
∵AC平分∠DAB∴∠DAC=∠OAC∴∠DAC=∠OCA,∴OC∥AD
∵AD⊥CD,∴OC⊥CD.又∵OC是⊙O的半径,∴直线CD与⊙O相切于点C
(2)解:连接BC,则∠ACB=90°.
∵∠DAC=∠OAC,∠ADC=∠ACB=90°,∴△ADC∽△ACB,
∴,∴.
16、解:(1)连接OD、OE,
∵O为AB的中点,E为BC的中点,∴OE为△ABC的中位线,
∴OE∥AC,∴∠DOE=∠ODA,∠BOE=∠A,
∵OA=OD∴∠A=∠ODA,∴∠DOE=∠BOE
∵OD=OB,OE=OE,∴△ODE≌△OBE,∴∠ODE=∠OBE
∵DE是⊙O的切线,∴∠ODE=∠OBE=90°
∴OB⊥BC,∴BC是⊙O的切线.
(2)当为等腰三角形(AB=BC)时四边形OBDE是正方形,证明如下:
连接BD,
∵AB是⊙O的直径,∴BD⊥AC,
∵AB=BC,∴D为AC的中点,
∵E为BC的中点,∴DE为△ABC的中位线,∴DE∥AB,
∵DE为⊙O的切线,∴OD⊥DE,∴OD⊥AB,∴∠DOB=∠OBE=∠ODE=90°,
∵OD=OB,∴四边形OBED为正方形.
