北京市第二十四中学人教A版高中数学必修四教案:1.3 三角函数的诱导公式
文档属性
| 名称 | 北京市第二十四中学人教A版高中数学必修四教案:1.3 三角函数的诱导公式 |  | |
| 格式 | zip | ||
| 文件大小 | 87.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-01 14:32:45 | ||
图片预览




文档简介
教学设计
课题名称
1.3三角函数的诱导公式
科目
数学
教学对象
高一(2)(4)
课时
3课时
设计者
董建钢
一、教材内容分析
诱导公式是三角函数中三角计算和三角恒等变换的基础,是化归与转化重要数学思想的体现,所以这节课的内容是学好三角函数的关键,十分重要.
二、教学目标
[课标要求]
[具体分析教学目标]
(1)知识技能:
借助单位圆,推导出正弦、余弦和正切的诱导公式,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题
(2)过程方法:
通过公式的应用,了解未知到已知、复杂到简单的转化过程,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力。
(3)情感、态度、价值观:
通过学习,培养学生思维的严谨性与科学性等思维品质以及孜孜以求的探索精神等良好的个性品质
三、学情分析
学生已学习了三角函数的定义和同角三角函数间的关系,虽然大多数概念掌握较好,但基本功掌握不扎实,运算能力不强,需教师逐步引入、循序渐进的引导。
四、教学过程
资源准备、教师活动、预计时间
学生活动、预计时间
设计意图
一、复习:
1. 三角函数的定义:在平面直角坐标系中,设点是任意角终边上异于原点的任意一点,那么
, ,
2. 终边相同的角同一个三角函数值之间的关系:
诱导公式1.
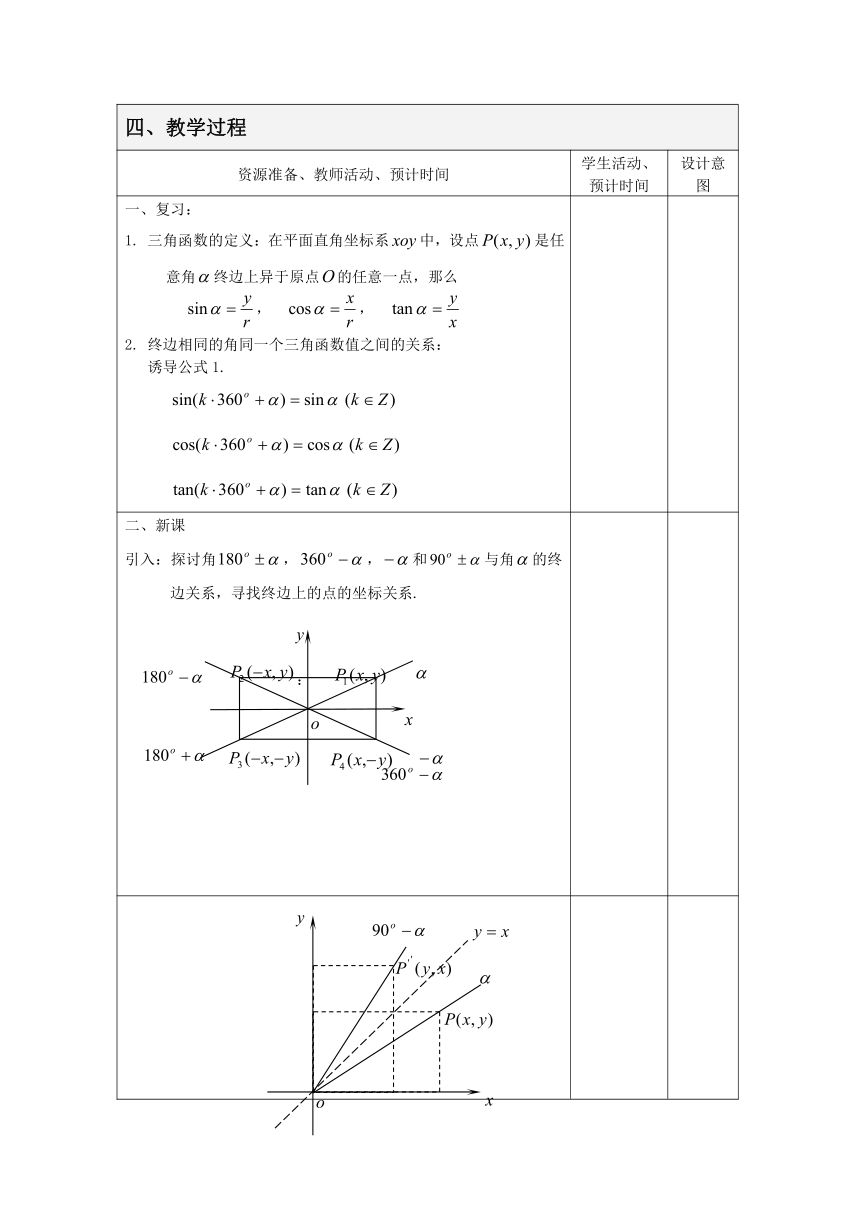
二、新课
引入:探讨角,,和与角的终边关系,寻找终边上的点的坐标关系.
1.由三角函数的定义得到:
因此有:诱导公式2.
,
诱导公式3.
,
诱导公式4.
,
诱导公式5.
,
诱导公式6.
,
诱导公式7.
,
三. 应用举例
例1. 求下列三角函数值
⑵ ⑶
例2. 已知,,
求的值。
例3. 化简
例4.已知,,则 __________.
例5.已知角的顶点在坐标原点,始边与轴正半轴重合,终边在直线上,则( )
A. B.2 C.0 D.
例6. 化简
例题小结:
在任意角的三角函数值的计算中,首先利用诱导公式①将任意的角 转化为之间的角;而后利用其它诱导公式②③④将之间的角转化为一个锐角的三角函数并计算.如遇负角可用诱导公式⑤转化为正角的三角函数进行;
在给值求值的计算中,先将所给的三角函数值的表达式化为最简形式,而后利用诱导公式化简所求三角函数式,最后根据同角三角函数间的关系和角所在的象限求值;
在三角函数式的化简过程中,根据诱导公式将所给的三角函数式化为同一个角的三角函数式化简.
练习1. 求值:
练习2. 求证:
练习3.诱导公式练习二
板书设计:
应用举例:
例1. 例2. 例3.
例4. 例5. 例6.
课堂小结:
诱导公式的含义:
任意角的三角函数 ∽角的三角函数 锐角的三角函数
方法归纳(见例题小结)
五、教学流程图
(一)、复习
(二)、新课引入
(三)、应用举例和练习
(四)、归纳小结和布置作业
六、教学评价设计
七、教学反思
教学设计
课题名称
1.3三角函数的诱导公式
科目
数学
教学对象
高一(2)(4)
课时
3课时
设计者
董建钢
一、教材内容分析
诱导公式是三角函数中三角计算和三角恒等变换的基础,是化归与转化重要数学思想的体现,所以这节课的内容是学好三角函数的关键,十分重要.
二、教学目标
[课标要求]
[具体分析教学目标]
(1)知识技能:
借助单位圆,推导出正弦、余弦和正切的诱导公式,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题
(2)过程方法:
通过公式的应用,了解未知到已知、复杂到简单的转化过程,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力。
(3)情感、态度、价值观:
通过学习,培养学生思维的严谨性与科学性等思维品质以及孜孜以求的探索精神等良好的个性品质
三、学情分析
学生已学习了三角函数的定义和同角三角函数间的关系,虽然大多数概念掌握较好,但基本功掌握不扎实,运算能力不强,需教师逐步引入、循序渐进的引导。
四、教学过程
资源准备、教师活动、预计时间
学生活动、预计时间
设计意图
一、复习:
1. 三角函数的定义:在平面直角坐标系中,设点是任意角终边上异于原点的任意一点,那么
, ,
2. 终边相同的角同一个三角函数值之间的关系:
诱导公式1.
二、新课
引入:探讨角,,和与角的终边关系,寻找终边上的点的坐标关系.
1.由三角函数的定义得到:
因此有:诱导公式2.
,
诱导公式3.
,
诱导公式4.
,
诱导公式5.
,
诱导公式6.
,
诱导公式7.
,
三. 应用举例
例1. 求下列三角函数值
⑵ ⑶
例2. 已知,,
求的值。
例3. 化简
例4.已知,,则 __________.
例5.已知角的顶点在坐标原点,始边与轴正半轴重合,终边在直线上,则( )
A. B.2 C.0 D.
例6. 化简
例题小结:
在任意角的三角函数值的计算中,首先利用诱导公式①将任意的角 转化为之间的角;而后利用其它诱导公式②③④将之间的角转化为一个锐角的三角函数并计算.如遇负角可用诱导公式⑤转化为正角的三角函数进行;
在给值求值的计算中,先将所给的三角函数值的表达式化为最简形式,而后利用诱导公式化简所求三角函数式,最后根据同角三角函数间的关系和角所在的象限求值;
在三角函数式的化简过程中,根据诱导公式将所给的三角函数式化为同一个角的三角函数式化简.
练习1. 求值:
练习2. 求证:
练习3.诱导公式练习二
板书设计:
应用举例:
例1. 例2. 例3.
例4. 例5. 例6.
课堂小结:
诱导公式的含义:
任意角的三角函数 ∽角的三角函数 锐角的三角函数
方法归纳(见例题小结)
五、教学流程图
(一)、复习
(二)、新课引入
(三)、应用举例和练习
(四)、归纳小结和布置作业
六、教学评价设计
七、教学反思
课题名称
1.3三角函数的诱导公式
科目
数学
教学对象
高一(2)(4)
课时
3课时
设计者
董建钢
一、教材内容分析
诱导公式是三角函数中三角计算和三角恒等变换的基础,是化归与转化重要数学思想的体现,所以这节课的内容是学好三角函数的关键,十分重要.
二、教学目标
[课标要求]
[具体分析教学目标]
(1)知识技能:
借助单位圆,推导出正弦、余弦和正切的诱导公式,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题
(2)过程方法:
通过公式的应用,了解未知到已知、复杂到简单的转化过程,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力。
(3)情感、态度、价值观:
通过学习,培养学生思维的严谨性与科学性等思维品质以及孜孜以求的探索精神等良好的个性品质
三、学情分析
学生已学习了三角函数的定义和同角三角函数间的关系,虽然大多数概念掌握较好,但基本功掌握不扎实,运算能力不强,需教师逐步引入、循序渐进的引导。
四、教学过程
资源准备、教师活动、预计时间
学生活动、预计时间
设计意图
一、复习:
1. 三角函数的定义:在平面直角坐标系中,设点是任意角终边上异于原点的任意一点,那么
, ,
2. 终边相同的角同一个三角函数值之间的关系:
诱导公式1.
二、新课
引入:探讨角,,和与角的终边关系,寻找终边上的点的坐标关系.
1.由三角函数的定义得到:
因此有:诱导公式2.
,
诱导公式3.
,
诱导公式4.
,
诱导公式5.
,
诱导公式6.
,
诱导公式7.
,
三. 应用举例
例1. 求下列三角函数值
⑵ ⑶
例2. 已知,,
求的值。
例3. 化简
例4.已知,,则 __________.
例5.已知角的顶点在坐标原点,始边与轴正半轴重合,终边在直线上,则( )
A. B.2 C.0 D.
例6. 化简
例题小结:
在任意角的三角函数值的计算中,首先利用诱导公式①将任意的角 转化为之间的角;而后利用其它诱导公式②③④将之间的角转化为一个锐角的三角函数并计算.如遇负角可用诱导公式⑤转化为正角的三角函数进行;
在给值求值的计算中,先将所给的三角函数值的表达式化为最简形式,而后利用诱导公式化简所求三角函数式,最后根据同角三角函数间的关系和角所在的象限求值;
在三角函数式的化简过程中,根据诱导公式将所给的三角函数式化为同一个角的三角函数式化简.
练习1. 求值:
练习2. 求证:
练习3.诱导公式练习二
板书设计:
应用举例:
例1. 例2. 例3.
例4. 例5. 例6.
课堂小结:
诱导公式的含义:
任意角的三角函数 ∽角的三角函数 锐角的三角函数
方法归纳(见例题小结)
五、教学流程图
(一)、复习
(二)、新课引入
(三)、应用举例和练习
(四)、归纳小结和布置作业
六、教学评价设计
七、教学反思
教学设计
课题名称
1.3三角函数的诱导公式
科目
数学
教学对象
高一(2)(4)
课时
3课时
设计者
董建钢
一、教材内容分析
诱导公式是三角函数中三角计算和三角恒等变换的基础,是化归与转化重要数学思想的体现,所以这节课的内容是学好三角函数的关键,十分重要.
二、教学目标
[课标要求]
[具体分析教学目标]
(1)知识技能:
借助单位圆,推导出正弦、余弦和正切的诱导公式,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题
(2)过程方法:
通过公式的应用,了解未知到已知、复杂到简单的转化过程,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力。
(3)情感、态度、价值观:
通过学习,培养学生思维的严谨性与科学性等思维品质以及孜孜以求的探索精神等良好的个性品质
三、学情分析
学生已学习了三角函数的定义和同角三角函数间的关系,虽然大多数概念掌握较好,但基本功掌握不扎实,运算能力不强,需教师逐步引入、循序渐进的引导。
四、教学过程
资源准备、教师活动、预计时间
学生活动、预计时间
设计意图
一、复习:
1. 三角函数的定义:在平面直角坐标系中,设点是任意角终边上异于原点的任意一点,那么
, ,
2. 终边相同的角同一个三角函数值之间的关系:
诱导公式1.
二、新课
引入:探讨角,,和与角的终边关系,寻找终边上的点的坐标关系.
1.由三角函数的定义得到:
因此有:诱导公式2.
,
诱导公式3.
,
诱导公式4.
,
诱导公式5.
,
诱导公式6.
,
诱导公式7.
,
三. 应用举例
例1. 求下列三角函数值
⑵ ⑶
例2. 已知,,
求的值。
例3. 化简
例4.已知,,则 __________.
例5.已知角的顶点在坐标原点,始边与轴正半轴重合,终边在直线上,则( )
A. B.2 C.0 D.
例6. 化简
例题小结:
在任意角的三角函数值的计算中,首先利用诱导公式①将任意的角 转化为之间的角;而后利用其它诱导公式②③④将之间的角转化为一个锐角的三角函数并计算.如遇负角可用诱导公式⑤转化为正角的三角函数进行;
在给值求值的计算中,先将所给的三角函数值的表达式化为最简形式,而后利用诱导公式化简所求三角函数式,最后根据同角三角函数间的关系和角所在的象限求值;
在三角函数式的化简过程中,根据诱导公式将所给的三角函数式化为同一个角的三角函数式化简.
练习1. 求值:
练习2. 求证:
练习3.诱导公式练习二
板书设计:
应用举例:
例1. 例2. 例3.
例4. 例5. 例6.
课堂小结:
诱导公式的含义:
任意角的三角函数 ∽角的三角函数 锐角的三角函数
方法归纳(见例题小结)
五、教学流程图
(一)、复习
(二)、新课引入
(三)、应用举例和练习
(四)、归纳小结和布置作业
六、教学评价设计
七、教学反思
