15.2第1课时利用平面直角坐标系解决几何问题(教学课件)-七年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 15.2第1课时利用平面直角坐标系解决几何问题(教学课件)-七年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 11:45:00 | ||
图片预览








文档简介
(共30张PPT)
15.2 利用平面直角坐标系解决几何问题
(第1课时)
2023-2024学年沪教版七年级下册数学课件
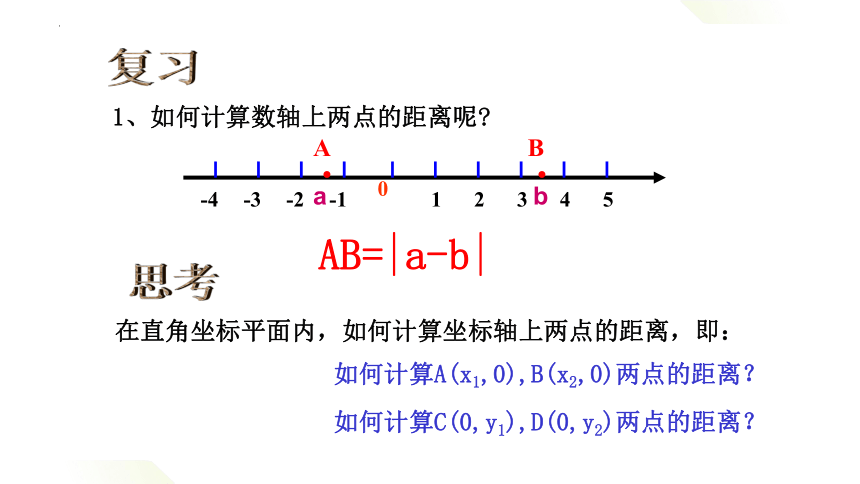
复习
1、如何计算数轴上两点的距离呢
0
1
2
3
4
5
-4
-3
-2
-1
·
B
·
A
a
b
AB=|a-b|
思考
在直角坐标平面内,如何计算坐标轴上两点的距离,即:
如何计算A(x1,0),B(x2,0)两点的距离?
如何计算C(0,y1),D(0,y2)两点的距离?
2、平行于坐标轴的直线上两点的坐标有什么特点
复行于x 轴的直线上两点A(x1,y1)、B(x2,y2)
的坐标特点:
② 平行于y 轴的直线上两点C(x3,y3)、D(x4,y4)
的坐标特点:
纵坐标相同,即:y1=y2。
横坐标相同,即:x3=x4。
思考
在直角坐标平面内,已知 x 轴上的两个点 A(x,0)和B(x2,0),Y轴上的两个点 C(0,)和 D(0,y,如何计算 A、B两点的距离以及 C、D 两点的距离呢
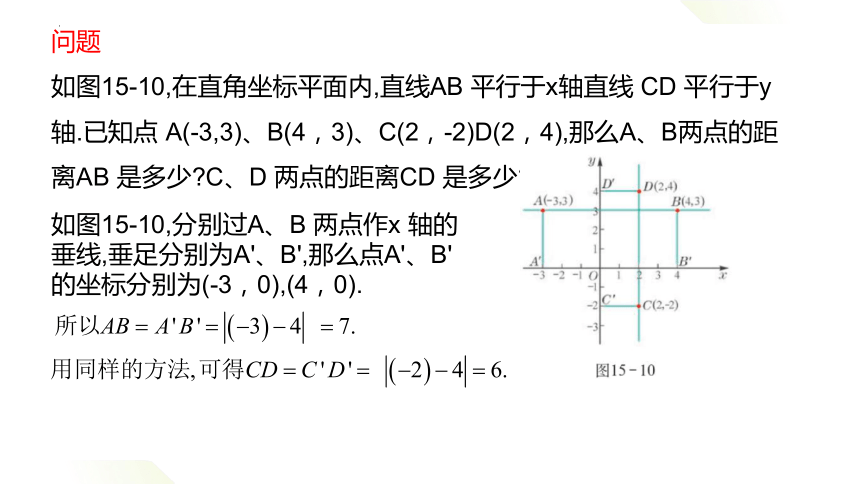
问题
如图15-10,在直角坐标平面内,直线AB 平行于x轴直线 CD 平行于y轴.已知点 A(-3,3)、B(4,3)、C(2,-2)D(2,4),那么A、B两点的距离AB 是多少 C、D 两点的距离CD 是多少
如图15-10,分别过A、B 两点作x 轴的垂线,垂足分别为A'、B',那么点A'、B'的坐标分别为(-3,0),(4,0).
在直角坐标平面内,
平行于坐标轴的直线上两点的距离计算公式:
① 平行于x 轴的直线上两点A(x1,y)、B(x2,y)的距离:
② 平行于y 轴的直线上两点C(x,y1)、D(x,y2)的距离:
概括
AB = |x1-x2|
CD = |y1-y2|
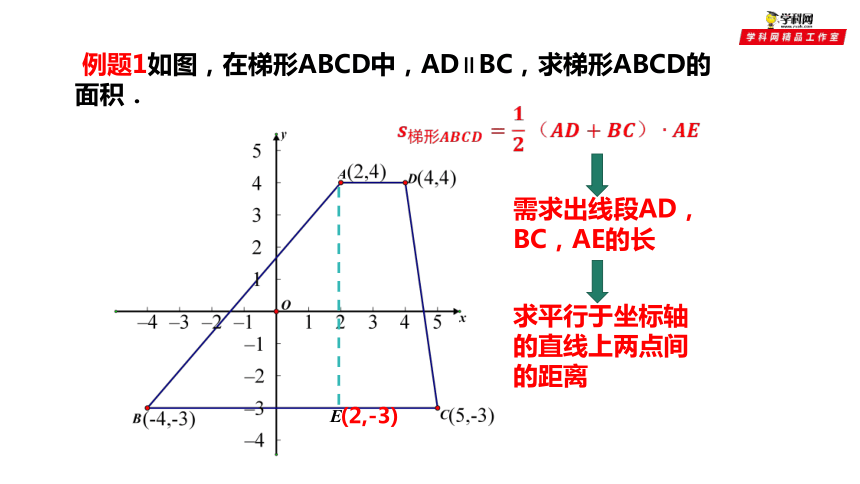
例题1如图,在梯形ABCD中,AD∥BC,求梯形ABCD的面积.
E
求平行于坐标轴的直线上两点间的距离
需求出线段AD,BC,AE的长
(2,-3)
解 画出梯形的高AE. 点A、B、C、D、E 的坐标分别为(2,4)、(-4,-3)、(5,-3)、(4,4)、(2,-3),因此
BC=|-4-5|=9,
AD=|2-4|=2,
AE= |4-(-3)|=7.
所以梯形ABCD的面积
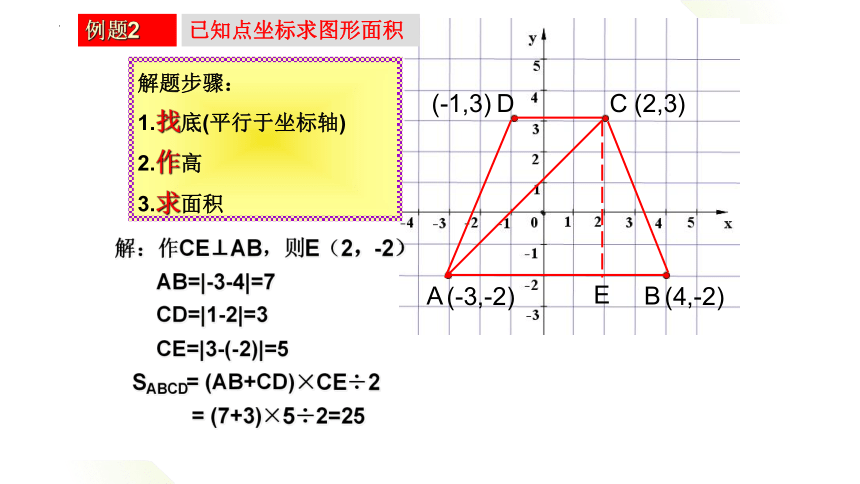
例题2
(1)如图,平面直角坐标系中有一个三角形,写出各点坐标,并求S△ABC
(4,-2)
(-3,-2)
(2,3)
已知点坐标求图形面积
E
(-1,3)
A
B
C
D
(2)如图,在梯形ABCD中,AB//CD, 求SABCD
解:作CE⊥AB,则E(2,-2)
AB=|-3-4|=7
CD=|1-2|=3
CE=|3-(-2)|=5
SABCD= (AB+CD)×CE÷2
= (7+3)×5÷2=25
解题步骤:
1.找底(平行于坐标轴)
2.作高
3.求面积
1.已知点A(1,2a+1),B(-a,a-3),若线段AB∥x轴,则三角形AOB的面积为( ____ )
A.21
B.28
C.14
D.10.5
【解析】解:∵AB∥x轴,
∴2a+1=a-3.解得a=-4.
∴A(1,-7),B(4,-7).
∴AB=3.
D
∴△AOB的面积为: ×3×7=10.5,
故选:D.
2.已知点A(1,3)与点B(x,y)在同一条平行于x轴的直线上,点B与A相距3个单位长度,则点B的坐标是( ____ )
A.(1,6)
B.(4,3)
C.(1,6)或(1,0)
D.(4,3)或(-2,3)
【解析】解:∵点A(1,3)与点B(x,y)在同一条平行于x轴的直线上,且点B与A相距3个单位长度,
∴y=3,|x-1|=3.
∴y=3,x=4或者x=-2.
D
∴点B的坐标为(4,3)或(-2,3).
故选:D.
3.我们规定:在平面直角坐标系xOy中,任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1-x2|+|y1-y2|,例如图中,点M(-2,3)与N(1,-1)之间的折线距离为d(M,N)=|-2-1|+|3-(-1)|=3+4=7.已知点P(-3,4),若点Q的坐标为(1,t),且d(P,Q)=8,则t的值为
( ____ )
A.0
B.-1
C.-1或7
D
D.0或8
【解析】解:∵点P(-3,4),点Q(1,t),d(P,Q)=8,
∴|-3-1|+|4-t|=8,
解得,t=0或t=8,
故选:D.
4.如图,点A(5,0),点B(4,3),点C(0,2),则四边形OABC的面积是 ______ .
【解析】解:连接OB,如图,
四边形OABC的面积=S△OBC+S△OAB
= ×2×4+ ×5×3
=11.5.
故答案为:11.5.
11.5
5.在平面直角坐标系中,我们把横纵坐标均为整数的点称为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.例如:图中△ABC的与四边形DEFG均为格点多边形.图中每个小正方形边长均为1.
(1)△ABC的面积为 ____ ,四边形DEFG的面积为 _____ .
(2)格点多边形的面积记为S,其内部的格点数记为N,边界上的格点记为L,已知格点多边形的面积可表示为S=N+aL+b(a,b为常数).由(1)中所求图形的面积求a,b的值.
(3)若某格点多边形对应的N=14,L=7,则S= ____ .
1
3.5
16
【解析】解:(1)△ABC的面积为 2×1=1,
四边形DEFG的面积为 ×(1+4)×2- ×1×1- ×2×1=3.5,
故答案为:1,3.5;
(2)由(1)可得,图中格点三角形ABC的面积为1,格点四边形DEFG的面积为3.5,
∵格点多边形的面积S=N+aL+b,
∴结合图中的格点三角形ABC及格点四边形DEFG可得, ,
∴ ;
(3)由(2)知,S=N+ L-1,
将N=14,L=7代入S=N+ L-1,得S=14+ -1= .
故答案为: .
6.阅读材料:
两点间的距离公式:如果平面直角坐标系内有两点A(x1,y1)、B(x2,y2),那么A、B两点的距离AB= ,则AB2=(x1-x2)2+(y1-y2)2.
例如:
若点A(4,1),B(3,2),则AB= ,
若点A(a,1),B(3,2),且AB= ,则 .
根据实数章节所学的开方运算即可求出满足条件的a的值.
根据上面材料完成下列各题:
(1)若点A(-2,3),B(1,2),则A、B两点间的距离是 .
(2)若点A(-2,3),点B在x轴上,且A、B两点间的距离是5,求B点坐标.
【解析】解:(1)∵A(-2,3),B(1,2),
∴AB= ,
故答案为: ;
(2)设B(m,n),
∵点B在轴上,
∴n=0,
∴B(m,0),
∵A(-2,3),且A、B两点间的距离是5,
∴52=(-2-m)2+(3-0)2,
整理得(-2-m)2=16,
∵± =±4,
∴-2-m=4或-2-m=-4,
∴m=-6或m=2,
∴B(-6,0)或B(2,0).
7.已知点A(-2,1),B(0,1),C(-2,4).
(1)求△ABC的面积;
(2)若点D在x轴上方,且S△ABD=S△ABC,请写出符合条件的点D的坐标,这样的点有什么特点?____
【解析】解:(1)如图:
____
∵点A(-2,1),B(0,1),C(-2,4),
∴∠CAB=90°,AB=0-(-2)=0+2=2,AC=4-1=3,
∴△ABC的面积= AC AB= ×3×2=3,
∴△ABC的面积为3;
(2)∵S△ABD=S△ABC,
∴点D到AB的距离=AC=3,
∵点D在x轴上方,
∴点D在直线y=4上,
∴符合条件的点D都在直线y=4上,这样的点的纵坐标都为4.
8.如图,在平面直角坐标系中,点A的坐标(0,a),点B的坐标(b,0),点C坐标(2,a),且a、b满足 ,CD⊥CB且CD=CB.
(1)点D的坐标为 ________ ,△ACD中的面积为 ____ .
(2)小明同学在学习求坐标平面内三角形面积时学到一个新方法如下:平面直角坐标系中有△P1P2P3,其三个顶点P1(x1,y1)、P2(x2,y2)、P3(x3,y3),按逆时针方向排列,则△P1P2P3的面积S可用下面式子计算,
(4,3)
1
,请用此方法计算△ABD的面积.
【解析】解:(1)∵ ,
又∵|a-2|≥0, ,
∴a-2=0且a-b+1=0,
∴a=2,b=3,
∴点A的坐标为(0,2),点B的坐标为(3,0),点C的坐标为(2,2),
∴AC=2,AC∥x轴,
如图,过点C作CE⊥x轴于点E,过点D作DH⊥AC交AC延长线于点H,
____
∴∠CEB=∠CHD=∠ECH=90°,CE=2,BE=1,
∵CD⊥CB,
∴∠BCD=90°,
∴∠BCD=∠ECH,
∴∠BCD-∠BCH=∠ECH-∠BCH,
∴∠HCD=∠ECB,
在△CEB和△CHD中,
,
∴△CEB≌△CHD(AAS),
∴CE=CH=2,BE=DH=1,
∴AH=4,
∴点D的坐标为(4,3),
∴ .
故答案为:(4,3),1;
(2)∵A(0,2),B(3,0),D(4,3),
∴x1=0,y1=2,x2=3,y2=0,x3=4,y3=3,
∵ ,
∴S= = .
故△ABD的面积为 .
谢谢
15.2 利用平面直角坐标系解决几何问题
(第1课时)
2023-2024学年沪教版七年级下册数学课件
复习
1、如何计算数轴上两点的距离呢
0
1
2
3
4
5
-4
-3
-2
-1
·
B
·
A
a
b
AB=|a-b|
思考
在直角坐标平面内,如何计算坐标轴上两点的距离,即:
如何计算A(x1,0),B(x2,0)两点的距离?
如何计算C(0,y1),D(0,y2)两点的距离?
2、平行于坐标轴的直线上两点的坐标有什么特点
复行于x 轴的直线上两点A(x1,y1)、B(x2,y2)
的坐标特点:
② 平行于y 轴的直线上两点C(x3,y3)、D(x4,y4)
的坐标特点:
纵坐标相同,即:y1=y2。
横坐标相同,即:x3=x4。
思考
在直角坐标平面内,已知 x 轴上的两个点 A(x,0)和B(x2,0),Y轴上的两个点 C(0,)和 D(0,y,如何计算 A、B两点的距离以及 C、D 两点的距离呢
问题
如图15-10,在直角坐标平面内,直线AB 平行于x轴直线 CD 平行于y轴.已知点 A(-3,3)、B(4,3)、C(2,-2)D(2,4),那么A、B两点的距离AB 是多少 C、D 两点的距离CD 是多少
如图15-10,分别过A、B 两点作x 轴的垂线,垂足分别为A'、B',那么点A'、B'的坐标分别为(-3,0),(4,0).
在直角坐标平面内,
平行于坐标轴的直线上两点的距离计算公式:
① 平行于x 轴的直线上两点A(x1,y)、B(x2,y)的距离:
② 平行于y 轴的直线上两点C(x,y1)、D(x,y2)的距离:
概括
AB = |x1-x2|
CD = |y1-y2|
例题1如图,在梯形ABCD中,AD∥BC,求梯形ABCD的面积.
E
求平行于坐标轴的直线上两点间的距离
需求出线段AD,BC,AE的长
(2,-3)
解 画出梯形的高AE. 点A、B、C、D、E 的坐标分别为(2,4)、(-4,-3)、(5,-3)、(4,4)、(2,-3),因此
BC=|-4-5|=9,
AD=|2-4|=2,
AE= |4-(-3)|=7.
所以梯形ABCD的面积
例题2
(1)如图,平面直角坐标系中有一个三角形,写出各点坐标,并求S△ABC
(4,-2)
(-3,-2)
(2,3)
已知点坐标求图形面积
E
(-1,3)
A
B
C
D
(2)如图,在梯形ABCD中,AB//CD, 求SABCD
解:作CE⊥AB,则E(2,-2)
AB=|-3-4|=7
CD=|1-2|=3
CE=|3-(-2)|=5
SABCD= (AB+CD)×CE÷2
= (7+3)×5÷2=25
解题步骤:
1.找底(平行于坐标轴)
2.作高
3.求面积
1.已知点A(1,2a+1),B(-a,a-3),若线段AB∥x轴,则三角形AOB的面积为( ____ )
A.21
B.28
C.14
D.10.5
【解析】解:∵AB∥x轴,
∴2a+1=a-3.解得a=-4.
∴A(1,-7),B(4,-7).
∴AB=3.
D
∴△AOB的面积为: ×3×7=10.5,
故选:D.
2.已知点A(1,3)与点B(x,y)在同一条平行于x轴的直线上,点B与A相距3个单位长度,则点B的坐标是( ____ )
A.(1,6)
B.(4,3)
C.(1,6)或(1,0)
D.(4,3)或(-2,3)
【解析】解:∵点A(1,3)与点B(x,y)在同一条平行于x轴的直线上,且点B与A相距3个单位长度,
∴y=3,|x-1|=3.
∴y=3,x=4或者x=-2.
D
∴点B的坐标为(4,3)或(-2,3).
故选:D.
3.我们规定:在平面直角坐标系xOy中,任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1-x2|+|y1-y2|,例如图中,点M(-2,3)与N(1,-1)之间的折线距离为d(M,N)=|-2-1|+|3-(-1)|=3+4=7.已知点P(-3,4),若点Q的坐标为(1,t),且d(P,Q)=8,则t的值为
( ____ )
A.0
B.-1
C.-1或7
D
D.0或8
【解析】解:∵点P(-3,4),点Q(1,t),d(P,Q)=8,
∴|-3-1|+|4-t|=8,
解得,t=0或t=8,
故选:D.
4.如图,点A(5,0),点B(4,3),点C(0,2),则四边形OABC的面积是 ______ .
【解析】解:连接OB,如图,
四边形OABC的面积=S△OBC+S△OAB
= ×2×4+ ×5×3
=11.5.
故答案为:11.5.
11.5
5.在平面直角坐标系中,我们把横纵坐标均为整数的点称为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.例如:图中△ABC的与四边形DEFG均为格点多边形.图中每个小正方形边长均为1.
(1)△ABC的面积为 ____ ,四边形DEFG的面积为 _____ .
(2)格点多边形的面积记为S,其内部的格点数记为N,边界上的格点记为L,已知格点多边形的面积可表示为S=N+aL+b(a,b为常数).由(1)中所求图形的面积求a,b的值.
(3)若某格点多边形对应的N=14,L=7,则S= ____ .
1
3.5
16
【解析】解:(1)△ABC的面积为 2×1=1,
四边形DEFG的面积为 ×(1+4)×2- ×1×1- ×2×1=3.5,
故答案为:1,3.5;
(2)由(1)可得,图中格点三角形ABC的面积为1,格点四边形DEFG的面积为3.5,
∵格点多边形的面积S=N+aL+b,
∴结合图中的格点三角形ABC及格点四边形DEFG可得, ,
∴ ;
(3)由(2)知,S=N+ L-1,
将N=14,L=7代入S=N+ L-1,得S=14+ -1= .
故答案为: .
6.阅读材料:
两点间的距离公式:如果平面直角坐标系内有两点A(x1,y1)、B(x2,y2),那么A、B两点的距离AB= ,则AB2=(x1-x2)2+(y1-y2)2.
例如:
若点A(4,1),B(3,2),则AB= ,
若点A(a,1),B(3,2),且AB= ,则 .
根据实数章节所学的开方运算即可求出满足条件的a的值.
根据上面材料完成下列各题:
(1)若点A(-2,3),B(1,2),则A、B两点间的距离是 .
(2)若点A(-2,3),点B在x轴上,且A、B两点间的距离是5,求B点坐标.
【解析】解:(1)∵A(-2,3),B(1,2),
∴AB= ,
故答案为: ;
(2)设B(m,n),
∵点B在轴上,
∴n=0,
∴B(m,0),
∵A(-2,3),且A、B两点间的距离是5,
∴52=(-2-m)2+(3-0)2,
整理得(-2-m)2=16,
∵± =±4,
∴-2-m=4或-2-m=-4,
∴m=-6或m=2,
∴B(-6,0)或B(2,0).
7.已知点A(-2,1),B(0,1),C(-2,4).
(1)求△ABC的面积;
(2)若点D在x轴上方,且S△ABD=S△ABC,请写出符合条件的点D的坐标,这样的点有什么特点?____
【解析】解:(1)如图:
____
∵点A(-2,1),B(0,1),C(-2,4),
∴∠CAB=90°,AB=0-(-2)=0+2=2,AC=4-1=3,
∴△ABC的面积= AC AB= ×3×2=3,
∴△ABC的面积为3;
(2)∵S△ABD=S△ABC,
∴点D到AB的距离=AC=3,
∵点D在x轴上方,
∴点D在直线y=4上,
∴符合条件的点D都在直线y=4上,这样的点的纵坐标都为4.
8.如图,在平面直角坐标系中,点A的坐标(0,a),点B的坐标(b,0),点C坐标(2,a),且a、b满足 ,CD⊥CB且CD=CB.
(1)点D的坐标为 ________ ,△ACD中的面积为 ____ .
(2)小明同学在学习求坐标平面内三角形面积时学到一个新方法如下:平面直角坐标系中有△P1P2P3,其三个顶点P1(x1,y1)、P2(x2,y2)、P3(x3,y3),按逆时针方向排列,则△P1P2P3的面积S可用下面式子计算,
(4,3)
1
,请用此方法计算△ABD的面积.
【解析】解:(1)∵ ,
又∵|a-2|≥0, ,
∴a-2=0且a-b+1=0,
∴a=2,b=3,
∴点A的坐标为(0,2),点B的坐标为(3,0),点C的坐标为(2,2),
∴AC=2,AC∥x轴,
如图,过点C作CE⊥x轴于点E,过点D作DH⊥AC交AC延长线于点H,
____
∴∠CEB=∠CHD=∠ECH=90°,CE=2,BE=1,
∵CD⊥CB,
∴∠BCD=90°,
∴∠BCD=∠ECH,
∴∠BCD-∠BCH=∠ECH-∠BCH,
∴∠HCD=∠ECB,
在△CEB和△CHD中,
,
∴△CEB≌△CHD(AAS),
∴CE=CH=2,BE=DH=1,
∴AH=4,
∴点D的坐标为(4,3),
∴ .
故答案为:(4,3),1;
(2)∵A(0,2),B(3,0),D(4,3),
∴x1=0,y1=2,x2=3,y2=0,x3=4,y3=3,
∵ ,
∴S= = .
故△ABD的面积为 .
谢谢
