15.2第2课时直角坐标平面内点的平移(教学课件)-七年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 15.2第2课时直角坐标平面内点的平移(教学课件)-七年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 11:47:15 | ||
图片预览










文档简介
(共40张PPT)
15.2 直角坐标平面内点的平移(第2课时)
2023-2024学年沪教版七年级下册数学课件
在直角坐标平面内:
平行于x轴(垂直于y轴)的直线上的两点A(x1,y),B(x2,y)的距离
平行于y轴(垂直于x轴)的直线上的两点C(x,y1),D(x,y2)的距离
知识回顾
AB = |x1-x2|
CD = |y1-y2|
在直角坐标平面内,
平行于坐标轴的直线上两点的距离计算公式:
① 平行于x 轴的直线上两点A(x1,y)、B(x2,y)的距离:
② 平行于y 轴的直线上两点C(x,y1)、D(x,y2)的距离:
概括
AB = |x1-x2|
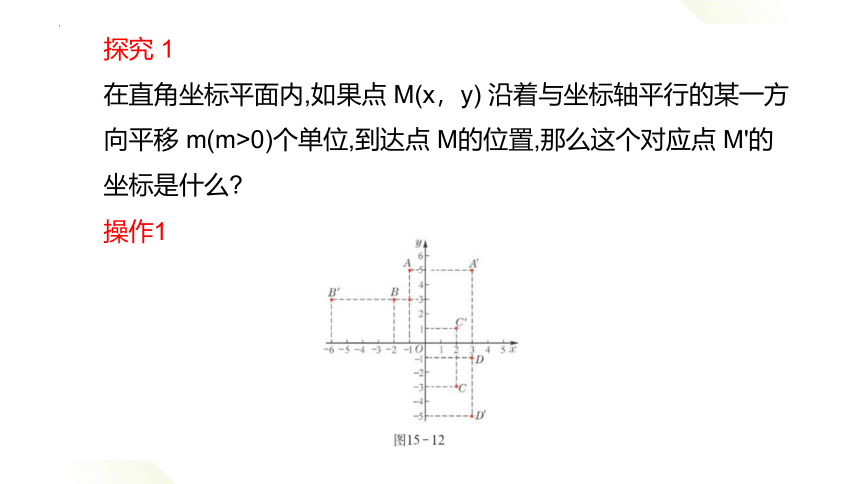
探究 1
在直角坐标平面内,如果点 M(x,y) 沿着与坐标轴平行的某一方向平移 m(m>0)个单位,到达点 M的位置,那么这个对应点 M'的坐标是什么
操作1
如图15-12,将点 A(-1,5) 向右平移4个单位,到达点A'的位置,这个点A'的坐标是(3,5);
将点 B(-2,3)向左平移4个单位,到达点 B的位置,这个点 B'的坐标是(-6,3);
将点 C(2,-3)向上平移4个单位,到达点 C的位置,这个点 C'的坐标是(2,1);
将点 D(3,-1)向下平移4个单位,到达点 D的位置,这个点 D的坐标是(3,-5).
向上平移所对应的点的坐标为( , )
向右平移所对应的点的坐标为( , )
在平面直角坐标系中,
一般地,如果点M(x,y)沿着与x轴或y轴平行的方向平移m(m>0)个单位,那么
x+m y
x y+m
概括
向左平移所对应的点的坐标为( , )
向下平移所对应的点的坐标为( , )
x-m y
x y-m
口诀:横移纵不变, 纵移横不变,
右加左减 , 上加下减。
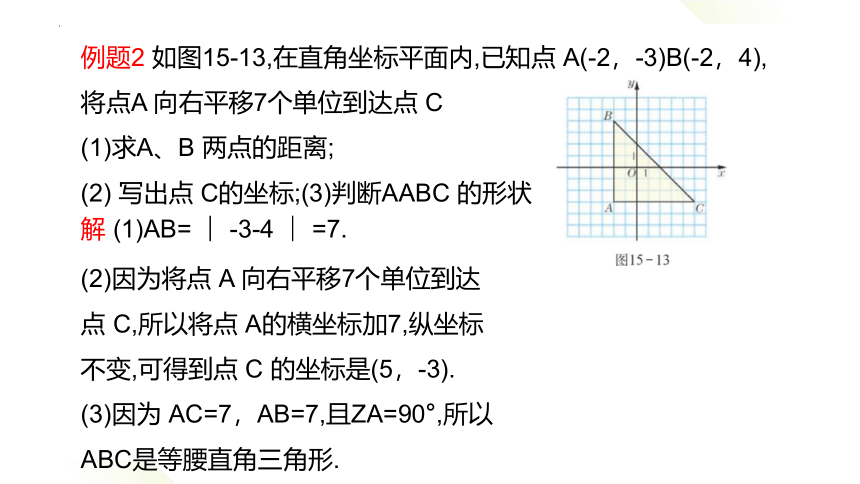
例题2 如图15-13,在直角坐标平面内,已知点 A(-2,-3)B(-2,4),将点A 向右平移7个单位到达点 C
(1)求A、B 两点的距离;
(2) 写出点 C的坐标;(3)判断AABC 的形状
解 (1)AB= | -3-4 | =7.
(2)因为将点 A 向右平移7个单位到达点 C,所以将点 A的横坐标加7,纵坐标不变,可得到点 C 的坐标是(5,-3).
(3)因为 AC=7,AB=7,且ZA=90°,所以ABC是等腰直角三角形.
在平面直角坐标系内,
如果把一个图形上的各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个长度单位;
如果把各点的纵坐标都加(或减去)一个正数a,相应的图形就是把原图形向上(或向下)平移a个单位长度.
归纳
1.已知 和|b+24|互为相反数,则点(a,b)向上平移3个单位长度,再向右平移7个单位长度后的坐标是( ____ )
A.(11,-17) B.(8,31)
C.(15,-21) D.(15,-31)
【解析】解:∵ +|b+24|=0, ≥0,|b+24|≥0,
∴a=8,b=-24,
∴(8,-24)向上平移3个单位长度,再向右平移7个单位长度后的坐标是(15,-21),
C
2.点A(2a-4,a+5)向下平移2个单位到点B,若B在x轴上,则点A的坐标是( ____ )
A.(2,8)
B.(0,8)
C.(-10,2)
D.(-10,0)
【解析】解:∵点A(2a-4,a+5)向下平移2个单位,得到B,B在x轴上,
∴a+5-2=0,
解得a=-3,
∴A(-10,2).
C
3.已知点A(-1,-2),B(3,4),将线段AB平移得到线段CD.若点A的对应点C在x轴上,点B的对应点D在y轴上,则点C的坐标是( ____ )
A.(-4,0)
B.(1,-5)
C.(2,-4)
D.(-3,1)
【解析】解:∵点A(-1,-2),B(3,4),将线段AB平移得到线段CD,点A的对应点C在x轴上,点B对应点D在y轴上,
∴点A的纵坐标加2,点B的横坐标减3,
∴点A的对应点C的坐标是(-1-3,-2+2),即(-4,0).
A
4.如图,等边△ABC的顶点A(1,1),B(3,1),规定把△ABC“先沿x轴翻折,再向右平移1个单位”为一次变换,这样连续经过2022次变换后,等边△ABC的顶点C的坐标为( ____ )
A.(2023, +1)
B.(2023,- -1)
C.(2024, +1)
D.(2024,- -1)
【解析】解:∵△ABC为等边三角形,A(1,1),B(3,1),
C
∴C(2, +1),
∵沿x轴翻折,再向右平移1个单位为一次变换,
∴第一次变换后:C(3,- -1),
第二次变换后:C(4, +1),
第三次变换后:C(5,- -1),
……,
由此变换规律为:
横坐标:每次变换后加一,
纵坐标:奇数次变换为- -1,偶数次变换后为 +1,
∴2022次变换后,纵坐标为 +1,横坐标为2+2022=2024,
∴C(2024, +1),
故选:C.
5.(1)①点P(-3,5)向上平移6个单位后的坐标是 ___________ ,落在第 ____ 象限.
②点P(-3,5)向下平移6个单位后的坐标是 ___________ ,落在第 ____ 象限.
③点P(-3,5)向 ____ 平移 ____ 个单位后,正好落在x轴上,坐标是 _________ .
④点P(-3,5)向左平移4个单位后的坐标是 _________ ,落在第 ____ 象限.
⑤点P(-3,5)向右平移4个单位后的坐标是 ________ ,落在第 ____ 象限.
⑥点P(-3,5)向 ____ 平移 ____ 个单位后,正好落在y轴上,坐标是
(-3,11)
二
(-3,-1)
三
下
5
(-3,0)
(-7,5)
二
(1,5)
一
右
3
________ .
(2)把点P(3,-2)先向左平移5个单位,再向上平移5个单位后得到点P',则点P'的坐标是 _________ .
【解析】解:(1)①点P(-3,5)向上平移6个单位后的坐标是(-3,11),落在第二象限.
②点P(-3,5)向下平移6个单位后的坐标是(-3,-1),落在第三象限.
③点P(-3,5)向下平移5个单位后,正好落在x轴上,坐标是(-3,0).
④点P(-3,5)向左平移4个单位后的坐标是(-7,5),落在第二象限.
⑤点P(-3,5)向右平移4个单位后的坐标是(1,5),落在第一象限.
⑥点P(-3,5)向右平移3个单位后,正好落在y轴上,坐标是(0,5).
(0,5)
(-2,3)
(2)把点P(3,-2)先向左平移5个单位,再向上平移5个单位后得到点P',则点P'的坐标是(-2,3).
故答案为:(1)①(-3,11),二;
②(-3,-1),三;
③下;5;(-3,0);
④(-7,5),二;
⑤(1,5),一;
⑥右,3,(0,5);
(2)(-2,3).
6.如图,点A(-4,0),B(-1,0),将线段AB平移后得到线段CD,点A的对应点C恰好落在y轴上,且四边形ABDC的面积为9,则D点坐标为 ________ .
【解析】解:∵A(-4,0),B(-1,0),
∴AB=3,AO=4,
设C纵坐标为a,
∵四边形ABDC的面积为9,
∴3a=9,
∴a=3,
∵C(0,3),
(3,3)
∴平移的方式为:右移4个单位、上移3个单位,
则D点坐标为(-1+4,0+3),即(3,3),
故答案为:(3,3).
7.A,B,C三点是同一个平面直角坐标系内不同的三点,A点在坐标轴上,点A向上平移三个单位长度,再向左平移4个单位长度就到了B点;直线BC∥y轴,且B和C点到x轴的距离相等;C点的横坐标、纵坐标互为相反数;则A点的坐标是 ___________________ .
【解析】解:当A点在x轴上时,设A(a,0),
∵点A向左平移4个单位长度,再向上平移3个单位长度就到了B点,
∴B(a-4,3),
∵直线BC∥y轴,
∴C点的横坐标是a-4,
∵C点的横坐标、纵坐标互为相反数,
(7,0)或(0,-7)
∴C(a-4,a-4),
∵点B和点C到x轴的距离相等,
∴3=|4-a|,
∴a=1或a=7,
∴A(1,0)或A(7,0),
当A(1,0)时,B(-3,3),C(-3,-3),不合题意;
当A点在y轴上时,设A(0,a),
∵点A向左平移4个单位长度,再向上平移3个单位长度就到了B点,
∴B(-4,3+a),
∵直线BC∥y轴,
∴C点的横坐标是-4,
∵C点的横坐标、纵坐标互为相反数,
∴C(-4,4),
∵点B和点C到x轴的距离相等,
∴|3+a|=4,
∴a=1或a=-7,
∴A(0,1)或A(0,-7),
当A(0,1)时,B(-4,4),C(-4,4),不合题意;
综上所述:A点的坐标为(7,0)或(0,-7).
故答案为:(7,0)或(0,-7).
8.将点A(m-2, )向左平移a(a>0)个单位长度,向上平移b(b>0)个单位长度,得到点A1(2m-3,2m+1),则m的取值范围是 _________ .
【解析】解:由题意 ,
∴ ,
∵a>0,b>0,
-5<m<1
∴ ,
解得-5<m<1,
故答案为:-5<m<1.
9.如图,将△ABC先向上平移8个单位得到△A1B1C1,再将△A1B1C1向右平移6个单位得到A2B2C2,写出各个三角形顶点的坐标.
A ___________ ;B ___________ ;C ___________ .
A1 _________ ;B1 _________ ;C1 _________ .
A2 ________ ;B2 _________ ;C2 ________ .
(-5,-5)
(-7,-4)
(-4,-3)
(-5,3)
(-7,4)
(-4,5)
(1,3)
(-1,4)
(2,5)
【解析】解:由图可得,A(-5,-5),B(-7,-4),C(-4,-3).
∵将△ABC向上平移8个单位得到△A1B1C1,
∴A1(-5,3),B1(-7,4),C1(-4,5),
∵将△A1B1C1向右平移6个单位得到A2B2C2,
∴A2(1,3),B2(-1,4),C2(2,5).
故答案为:(-5,-5);(-7,-4);(-4,-3);(-5,3);(-7,4);(-4,5);(1,3);(-1,4);(2,5).
10.在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A的坐标是(-3,4),现将△ABC平移,使得点A变换为点A',点B'、C'分别是点B、C的对应点.
(1)请画出平移后的三角形A'B'C'(不写画法);
(2)点B'的坐标为 _________ ;点C'的坐标为 _________ ;
(3)若△ABC内部一点P的坐标为(a,b),则点P的对应点P'的坐标为 ______________ .
(3,-2)
(5,-5)
(a+9,b-3)
【解析】解:(1)如图,△A'B'C'即为所求.
___
(2)由图可得,B'(3,-2),C'(5,-5).
故答案为:(3,-2);(5,-5).
(3)∵△ABC是向右平移9个单位,向下平移3个单位得到的△A'B'C',
∴P'(a+9,b-3).
故答案为:(a+9,b-3).
11.如图,点A(0,2)、B(4,0),平移线段AB,将点A平移到点C(-3,0),点B平移到点D,CD交y轴于点E.
(1)求点D的坐标;
(2)P为x轴上一动点,若S△ABP=5,求点P的坐标.
【解析】解:(1)∵A(0,2),将线段AB平移,使A平移到C(-3,0),
∴平移规律为向左3个单位,向下2个单位,
∵B(4,0),4-3=1,0-2=-2,
∴点D的坐标为(1,-2);
(2)设P点坐标为(x,0),则BP=|x-4|,
∵S△ABP=5,
∴ ×|x-4|×2=5,
解得x=-1或9,
∴P点坐标为(-1,0)或(9,0).
12.平行四边形的三个顶点坐标分别是(-2,0),(-2,4),(4,-1),请直接画出平行四边形并写出第四个顶点的坐标.
【解析】解:如图,设点(-2,0)为点A,点(-2,4)为点B,点(4,-1)为点C,
连接AB,AC,BC,
可得AB=4,
当以BC为对角线时,在点C的正上方取点D',使CD'∥AB且CD'=AB,
即可得平行四边形ABD'C如图所示;
当以AC为对角线时,在点C的正下方取点D'',使CD''∥AB且CD''=AB,
即可得平行四边形ABCD''如图所示.
则平行四边形ABD'C和平行四边形ABCD''即为所求.
∴第四个顶点的坐标为(4,3)或(4,-5).
13.对于平面直角坐标系xOy中的图形G和点P,给出如下定义:将图形G沿上、下、左、右四个方向中的任意一个方向平移一次,平移距离小于或者等于1个单位长度,平移后的图形记为G′,若点P在图形G'上,则称点P为图形G的稳定点.例如,当图形G为点(-2,3)时,点M(-1,3),N(-2,3.5)都是图形G的稳定点(点M(-1,3)在图形G向右平移一个单位长度得到的图形G′上;点N(-2,3.5)在图形G向上平移0.5单位长度得到的图形G′上).
(1)已知点A(-1,0),B(3,0).
①在点P1(-2,0),P2(4,0),P3(1, ),P4( )中,线段AB的稳定点是 .
②若将线段AB向上平移t个单位长度,使得点E(0,2)或者点F(0,7)为线段AB的稳定点,写出t的取值范围 .
(2)边长为a的正方形,一个顶点是原点O,相邻两边分别在x轴、y轴的正半轴上,这个正方形及其内部记为图形G.若以(0,3),(5,0)为端点的线段上的所有点都是这个图形G的稳定点,直接写出a的最小值 .
【解析】解:(1)①如图1中,
___
观察图象,根据图形G的稳定点的定义可知:P1,P2,P3 是线段AB的稳定点.
故答案为:P1,P2,P3;
②如图2中,
__
观察图象可知当1≤t≤3或6≤t≤8时,点E(0,2)或者点F(0,7)
为线段AB的稳定点.
故答案为:1≤t≤3或6≤t≤8;
(2)如图3中,正方形OABC的边长为a,P(0,3),Q(5,0),
___
观察图象可知当a≥4时,线段PQ上的点都是图形G的稳定点.
∴a的最小值为4,
故答案为4.
谢谢
15.2 直角坐标平面内点的平移(第2课时)
2023-2024学年沪教版七年级下册数学课件
在直角坐标平面内:
平行于x轴(垂直于y轴)的直线上的两点A(x1,y),B(x2,y)的距离
平行于y轴(垂直于x轴)的直线上的两点C(x,y1),D(x,y2)的距离
知识回顾
AB = |x1-x2|
CD = |y1-y2|
在直角坐标平面内,
平行于坐标轴的直线上两点的距离计算公式:
① 平行于x 轴的直线上两点A(x1,y)、B(x2,y)的距离:
② 平行于y 轴的直线上两点C(x,y1)、D(x,y2)的距离:
概括
AB = |x1-x2|
探究 1
在直角坐标平面内,如果点 M(x,y) 沿着与坐标轴平行的某一方向平移 m(m>0)个单位,到达点 M的位置,那么这个对应点 M'的坐标是什么
操作1
如图15-12,将点 A(-1,5) 向右平移4个单位,到达点A'的位置,这个点A'的坐标是(3,5);
将点 B(-2,3)向左平移4个单位,到达点 B的位置,这个点 B'的坐标是(-6,3);
将点 C(2,-3)向上平移4个单位,到达点 C的位置,这个点 C'的坐标是(2,1);
将点 D(3,-1)向下平移4个单位,到达点 D的位置,这个点 D的坐标是(3,-5).
向上平移所对应的点的坐标为( , )
向右平移所对应的点的坐标为( , )
在平面直角坐标系中,
一般地,如果点M(x,y)沿着与x轴或y轴平行的方向平移m(m>0)个单位,那么
x+m y
x y+m
概括
向左平移所对应的点的坐标为( , )
向下平移所对应的点的坐标为( , )
x-m y
x y-m
口诀:横移纵不变, 纵移横不变,
右加左减 , 上加下减。
例题2 如图15-13,在直角坐标平面内,已知点 A(-2,-3)B(-2,4),将点A 向右平移7个单位到达点 C
(1)求A、B 两点的距离;
(2) 写出点 C的坐标;(3)判断AABC 的形状
解 (1)AB= | -3-4 | =7.
(2)因为将点 A 向右平移7个单位到达点 C,所以将点 A的横坐标加7,纵坐标不变,可得到点 C 的坐标是(5,-3).
(3)因为 AC=7,AB=7,且ZA=90°,所以ABC是等腰直角三角形.
在平面直角坐标系内,
如果把一个图形上的各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个长度单位;
如果把各点的纵坐标都加(或减去)一个正数a,相应的图形就是把原图形向上(或向下)平移a个单位长度.
归纳
1.已知 和|b+24|互为相反数,则点(a,b)向上平移3个单位长度,再向右平移7个单位长度后的坐标是( ____ )
A.(11,-17) B.(8,31)
C.(15,-21) D.(15,-31)
【解析】解:∵ +|b+24|=0, ≥0,|b+24|≥0,
∴a=8,b=-24,
∴(8,-24)向上平移3个单位长度,再向右平移7个单位长度后的坐标是(15,-21),
C
2.点A(2a-4,a+5)向下平移2个单位到点B,若B在x轴上,则点A的坐标是( ____ )
A.(2,8)
B.(0,8)
C.(-10,2)
D.(-10,0)
【解析】解:∵点A(2a-4,a+5)向下平移2个单位,得到B,B在x轴上,
∴a+5-2=0,
解得a=-3,
∴A(-10,2).
C
3.已知点A(-1,-2),B(3,4),将线段AB平移得到线段CD.若点A的对应点C在x轴上,点B的对应点D在y轴上,则点C的坐标是( ____ )
A.(-4,0)
B.(1,-5)
C.(2,-4)
D.(-3,1)
【解析】解:∵点A(-1,-2),B(3,4),将线段AB平移得到线段CD,点A的对应点C在x轴上,点B对应点D在y轴上,
∴点A的纵坐标加2,点B的横坐标减3,
∴点A的对应点C的坐标是(-1-3,-2+2),即(-4,0).
A
4.如图,等边△ABC的顶点A(1,1),B(3,1),规定把△ABC“先沿x轴翻折,再向右平移1个单位”为一次变换,这样连续经过2022次变换后,等边△ABC的顶点C的坐标为( ____ )
A.(2023, +1)
B.(2023,- -1)
C.(2024, +1)
D.(2024,- -1)
【解析】解:∵△ABC为等边三角形,A(1,1),B(3,1),
C
∴C(2, +1),
∵沿x轴翻折,再向右平移1个单位为一次变换,
∴第一次变换后:C(3,- -1),
第二次变换后:C(4, +1),
第三次变换后:C(5,- -1),
……,
由此变换规律为:
横坐标:每次变换后加一,
纵坐标:奇数次变换为- -1,偶数次变换后为 +1,
∴2022次变换后,纵坐标为 +1,横坐标为2+2022=2024,
∴C(2024, +1),
故选:C.
5.(1)①点P(-3,5)向上平移6个单位后的坐标是 ___________ ,落在第 ____ 象限.
②点P(-3,5)向下平移6个单位后的坐标是 ___________ ,落在第 ____ 象限.
③点P(-3,5)向 ____ 平移 ____ 个单位后,正好落在x轴上,坐标是 _________ .
④点P(-3,5)向左平移4个单位后的坐标是 _________ ,落在第 ____ 象限.
⑤点P(-3,5)向右平移4个单位后的坐标是 ________ ,落在第 ____ 象限.
⑥点P(-3,5)向 ____ 平移 ____ 个单位后,正好落在y轴上,坐标是
(-3,11)
二
(-3,-1)
三
下
5
(-3,0)
(-7,5)
二
(1,5)
一
右
3
________ .
(2)把点P(3,-2)先向左平移5个单位,再向上平移5个单位后得到点P',则点P'的坐标是 _________ .
【解析】解:(1)①点P(-3,5)向上平移6个单位后的坐标是(-3,11),落在第二象限.
②点P(-3,5)向下平移6个单位后的坐标是(-3,-1),落在第三象限.
③点P(-3,5)向下平移5个单位后,正好落在x轴上,坐标是(-3,0).
④点P(-3,5)向左平移4个单位后的坐标是(-7,5),落在第二象限.
⑤点P(-3,5)向右平移4个单位后的坐标是(1,5),落在第一象限.
⑥点P(-3,5)向右平移3个单位后,正好落在y轴上,坐标是(0,5).
(0,5)
(-2,3)
(2)把点P(3,-2)先向左平移5个单位,再向上平移5个单位后得到点P',则点P'的坐标是(-2,3).
故答案为:(1)①(-3,11),二;
②(-3,-1),三;
③下;5;(-3,0);
④(-7,5),二;
⑤(1,5),一;
⑥右,3,(0,5);
(2)(-2,3).
6.如图,点A(-4,0),B(-1,0),将线段AB平移后得到线段CD,点A的对应点C恰好落在y轴上,且四边形ABDC的面积为9,则D点坐标为 ________ .
【解析】解:∵A(-4,0),B(-1,0),
∴AB=3,AO=4,
设C纵坐标为a,
∵四边形ABDC的面积为9,
∴3a=9,
∴a=3,
∵C(0,3),
(3,3)
∴平移的方式为:右移4个单位、上移3个单位,
则D点坐标为(-1+4,0+3),即(3,3),
故答案为:(3,3).
7.A,B,C三点是同一个平面直角坐标系内不同的三点,A点在坐标轴上,点A向上平移三个单位长度,再向左平移4个单位长度就到了B点;直线BC∥y轴,且B和C点到x轴的距离相等;C点的横坐标、纵坐标互为相反数;则A点的坐标是 ___________________ .
【解析】解:当A点在x轴上时,设A(a,0),
∵点A向左平移4个单位长度,再向上平移3个单位长度就到了B点,
∴B(a-4,3),
∵直线BC∥y轴,
∴C点的横坐标是a-4,
∵C点的横坐标、纵坐标互为相反数,
(7,0)或(0,-7)
∴C(a-4,a-4),
∵点B和点C到x轴的距离相等,
∴3=|4-a|,
∴a=1或a=7,
∴A(1,0)或A(7,0),
当A(1,0)时,B(-3,3),C(-3,-3),不合题意;
当A点在y轴上时,设A(0,a),
∵点A向左平移4个单位长度,再向上平移3个单位长度就到了B点,
∴B(-4,3+a),
∵直线BC∥y轴,
∴C点的横坐标是-4,
∵C点的横坐标、纵坐标互为相反数,
∴C(-4,4),
∵点B和点C到x轴的距离相等,
∴|3+a|=4,
∴a=1或a=-7,
∴A(0,1)或A(0,-7),
当A(0,1)时,B(-4,4),C(-4,4),不合题意;
综上所述:A点的坐标为(7,0)或(0,-7).
故答案为:(7,0)或(0,-7).
8.将点A(m-2, )向左平移a(a>0)个单位长度,向上平移b(b>0)个单位长度,得到点A1(2m-3,2m+1),则m的取值范围是 _________ .
【解析】解:由题意 ,
∴ ,
∵a>0,b>0,
-5<m<1
∴ ,
解得-5<m<1,
故答案为:-5<m<1.
9.如图,将△ABC先向上平移8个单位得到△A1B1C1,再将△A1B1C1向右平移6个单位得到A2B2C2,写出各个三角形顶点的坐标.
A ___________ ;B ___________ ;C ___________ .
A1 _________ ;B1 _________ ;C1 _________ .
A2 ________ ;B2 _________ ;C2 ________ .
(-5,-5)
(-7,-4)
(-4,-3)
(-5,3)
(-7,4)
(-4,5)
(1,3)
(-1,4)
(2,5)
【解析】解:由图可得,A(-5,-5),B(-7,-4),C(-4,-3).
∵将△ABC向上平移8个单位得到△A1B1C1,
∴A1(-5,3),B1(-7,4),C1(-4,5),
∵将△A1B1C1向右平移6个单位得到A2B2C2,
∴A2(1,3),B2(-1,4),C2(2,5).
故答案为:(-5,-5);(-7,-4);(-4,-3);(-5,3);(-7,4);(-4,5);(1,3);(-1,4);(2,5).
10.在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A的坐标是(-3,4),现将△ABC平移,使得点A变换为点A',点B'、C'分别是点B、C的对应点.
(1)请画出平移后的三角形A'B'C'(不写画法);
(2)点B'的坐标为 _________ ;点C'的坐标为 _________ ;
(3)若△ABC内部一点P的坐标为(a,b),则点P的对应点P'的坐标为 ______________ .
(3,-2)
(5,-5)
(a+9,b-3)
【解析】解:(1)如图,△A'B'C'即为所求.
___
(2)由图可得,B'(3,-2),C'(5,-5).
故答案为:(3,-2);(5,-5).
(3)∵△ABC是向右平移9个单位,向下平移3个单位得到的△A'B'C',
∴P'(a+9,b-3).
故答案为:(a+9,b-3).
11.如图,点A(0,2)、B(4,0),平移线段AB,将点A平移到点C(-3,0),点B平移到点D,CD交y轴于点E.
(1)求点D的坐标;
(2)P为x轴上一动点,若S△ABP=5,求点P的坐标.
【解析】解:(1)∵A(0,2),将线段AB平移,使A平移到C(-3,0),
∴平移规律为向左3个单位,向下2个单位,
∵B(4,0),4-3=1,0-2=-2,
∴点D的坐标为(1,-2);
(2)设P点坐标为(x,0),则BP=|x-4|,
∵S△ABP=5,
∴ ×|x-4|×2=5,
解得x=-1或9,
∴P点坐标为(-1,0)或(9,0).
12.平行四边形的三个顶点坐标分别是(-2,0),(-2,4),(4,-1),请直接画出平行四边形并写出第四个顶点的坐标.
【解析】解:如图,设点(-2,0)为点A,点(-2,4)为点B,点(4,-1)为点C,
连接AB,AC,BC,
可得AB=4,
当以BC为对角线时,在点C的正上方取点D',使CD'∥AB且CD'=AB,
即可得平行四边形ABD'C如图所示;
当以AC为对角线时,在点C的正下方取点D'',使CD''∥AB且CD''=AB,
即可得平行四边形ABCD''如图所示.
则平行四边形ABD'C和平行四边形ABCD''即为所求.
∴第四个顶点的坐标为(4,3)或(4,-5).
13.对于平面直角坐标系xOy中的图形G和点P,给出如下定义:将图形G沿上、下、左、右四个方向中的任意一个方向平移一次,平移距离小于或者等于1个单位长度,平移后的图形记为G′,若点P在图形G'上,则称点P为图形G的稳定点.例如,当图形G为点(-2,3)时,点M(-1,3),N(-2,3.5)都是图形G的稳定点(点M(-1,3)在图形G向右平移一个单位长度得到的图形G′上;点N(-2,3.5)在图形G向上平移0.5单位长度得到的图形G′上).
(1)已知点A(-1,0),B(3,0).
①在点P1(-2,0),P2(4,0),P3(1, ),P4( )中,线段AB的稳定点是 .
②若将线段AB向上平移t个单位长度,使得点E(0,2)或者点F(0,7)为线段AB的稳定点,写出t的取值范围 .
(2)边长为a的正方形,一个顶点是原点O,相邻两边分别在x轴、y轴的正半轴上,这个正方形及其内部记为图形G.若以(0,3),(5,0)为端点的线段上的所有点都是这个图形G的稳定点,直接写出a的最小值 .
【解析】解:(1)①如图1中,
___
观察图象,根据图形G的稳定点的定义可知:P1,P2,P3 是线段AB的稳定点.
故答案为:P1,P2,P3;
②如图2中,
__
观察图象可知当1≤t≤3或6≤t≤8时,点E(0,2)或者点F(0,7)
为线段AB的稳定点.
故答案为:1≤t≤3或6≤t≤8;
(2)如图3中,正方形OABC的边长为a,P(0,3),Q(5,0),
___
观察图象可知当a≥4时,线段PQ上的点都是图形G的稳定点.
∴a的最小值为4,
故答案为4.
谢谢
