22.8平面向量的加法(第1课时)(教学课件)-八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 22.8平面向量的加法(第1课时)(教学课件)-八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 22章 四边形
22.8 平面向量的加法(第1课时)
学习目标
(1)初步掌握向量加法的三角形法则。
(2)学会用作图的方法求两个向量的和向量。
(3)知道向量的加法满足交换律与结合律;并会用它们进行向量的运算。
(4)知道零向量的意义及零向量的特征。
问:长度、面积、体积在确定度量单位后,它们只有大小,可以用一个数来表示.这些量中的同一类量,都可以进行加减运算,而向量不仅有大小,还有方向,两个向量可以相加吗?
这些量称为”数量”又称为“标量”
情景引入
问题1:小明从A地出发向东行走5千米到达B地,再向北又走了5千米到达C地.那么小明这时在A地的什么方向上?到A地的距离是多少?
问1:小明从A地到达B地是不是一次位置移动?从A移动到B的方向是什么?大小又是多少?
是,以A为起点,方向是向东,大小是5千米.
问2:从B地移动到C地是不是又是一次位置移动?方向是什么?大小又是多少?
是,以B为起点,方向是向北,大小是5千米.
根据移动的方向和距离,我们可以把上面的两次移动用向量 和向量 来表示.
如何画有向线段?
(1)定比例尺;(2)取定起点并以它为端点按指定方向画射线;(3)按比例尺截取线段;(4)在线段另一端点画上箭头.
取1:250 000的比例尺,可以画出有向线段来表示向量 和 ,再把起点A和终点C用有向线段连起来,画出有向线段 .
5千米按比例尺截取线段的长度如何计算?
5千米长度如何在纸上表示?
问3:那么这个向量 表示什么?
表示以A为起点,A地到C地的一次位置移动.
问4:如何计算 的大小和方向?
由图可知:△ABC是直角三角形,∠B=90°AB=BC=5(千米),于是可得∠A=45°,AC= (千米),所以,向量 :东北方向,7千米.
从A地到B地,再从B地到C地这两次位置移动合在一起,其结果就是从A地到C地进行了一次位置移动,用向量来表示,就说“向量 与 合在一起是向量 ”,这时称 为 和 的和向量,可表示为 + = .
小明从A地出发向东行走5千米到达B地,再向北又走了5千米到达C地.那么小明这时在A地的什么方向上?A地的距离是多少?
A
B
C
北
东
向东行走5千米
向北行走5千米
定义:求两个向量的和向量的运算叫做向量的加法.
问题2:已知向量 和 ,怎样求这两个向量的和向量?
问:从问题1中我们可以得到启示,当我们把两个位置向量首尾相接时,它们的和向量很容易确定.但是我们如何把这两个向量首尾相接呢?
可以通过平移的方法.
如果 与 是不平行的向量,那么,在平面内任取一点O,作向量 ,使 = ,再作向量 ,以O为起点、B为终点画有向线段 ,则有向线段 所表示的向量 是向量 与向量 的和向量.用算式表示为:
O
B
A
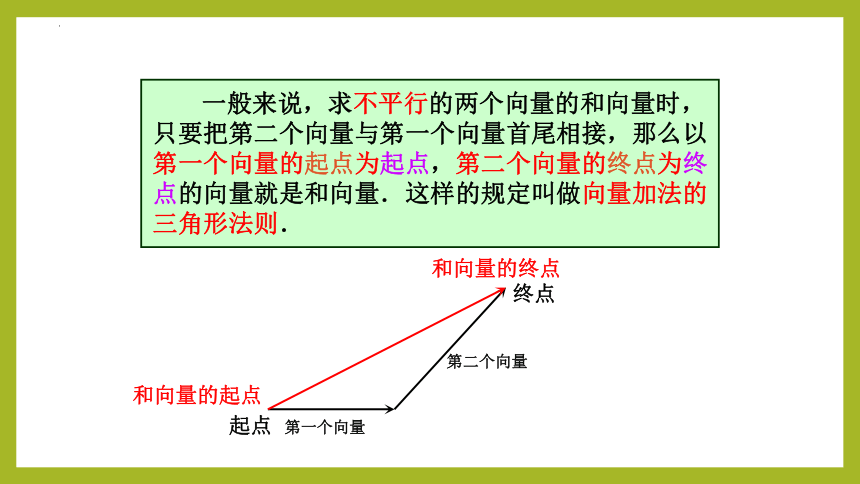
一般来说,求不平行的两个向量的和向量时,只要把第二个向量与第一个向量首尾相接,那么以第一个向量的起点为起点,第二个向量的终点为终点的向量就是和向量.这样的规定叫做向量加法的三角形法则.
起点
第一个向量
终点
和向量的起点
和向量的终点
第二个向量
运用三角形法则的一般步骤:
1、画出表示第一个向量的有向线段;
2、以第一条有向线段的终点作为第二条有向线段的起点(即首尾相接);
3、以第一条有向线段的起点为起点,第二条有向线段的终点为终点画有向线段.
问:如果不作图,你能否直接求出
能,第一条有向线段的终点恰好是第二条有向线段的起点(即首尾相接)
A
A
探究新知
问:如果给出两个平行的向量 和 ,那么如何求他们的和向量?
两个平行向量也可像上面作图一样,此时,向量 、
、 在一条直线上,我们仍规定 .
O A
B
O A
B
∴所求
∴所求
问:当 与 有特殊的关系时,它们的和向量是什么?
当 与 是相等向量时, + = + =2 .
当 与 是互为相反向量时, + = + = .
0
0是向量吗?
互为相反向量的两个向量的和是特殊的向量.
我们把长度为零的向量叫做零向量,记作 .规定 的方向可以是任意的(或者说不确定的); .于是,
问:0和 的区别是什么?
零向量有大小和方向,零只有大小;零向量的模是零.
对于任意的向量,都有 , .
1.两个向量相加,结果一定还是向量;
2.零向量 和实数0的区别在于,零向量不仅表示大小是零,它还有方向,它的方向是任意的.
例题1
如图,已知向量 和 .求作:
(1) (2)
解:(1)在平面内任取一点A,作向量 , ,再作
∴所求 .
A
B
C
例题1
如图,已知向量 和 .求作:
(1) (2)
解:(2)在平面内任取一点D,作向量 , ,再作
∴所求 .
此题运用向量加法的三角形法则.还有其他做法吗?
D
E
F
例题1
如图,已知向量 和 .求作:
(1) (2)
解法2:(2)以AB,BC为邻边,作平行四边形ABCD,再作向量 、 .
∴所求 .
为什么?
∵ABCD是平行四边形,
∴AD//BC,AD=BC;DC//AB;DC=AB.
∴
得
由此我们发现: = ,向量的加法满足交换律.
A
B
C
D
例题2
如图,已知向量 ,求作:
(1) ;
(2)
解:(1)在平面内任取一点O,作向量 , ,得 ;再作 ,然后作向量 ,则
.
请同学先试一试!
(2)作向量 ,得 ,则 .
由此我们发现: ,向量的加法满足结合律.
O
A
B
C
你能先在题1的图形上找到 的和向量吗?
由向量加法的交换律和结合律,可知三个向量相加,运算时可先将其中任意两个向量相加,所得的和向量再与第三个向量相加.
三个向量 、 、 相加,可表示为
.
课本练习
2.如图,已知平行四边形ABCD,在图中作出下列两个向量的和向量.
(1) , ;(2) .
(1)
(2)
∴ 是所求作的向量
如何首尾相接?
∴ 是所求作的向量
运用向量加法的交换律
∴ 是所求作的向量
E
3、填空:
1.下列判断中,不正确的是( ____ )
A. = B. =
C.如果| |=| |,那么 D. +( )=( )
【解析】
解:∵ = , , ,
∴A、B、D正确,
C
随堂检测
∵| |=| |,
∴ 或 ,
故C错误,
故选:C.
2.在矩形ABCD中, , ,则向量 的长度为( ____ )
A.2 B.4 C. D.
【解析】解:在矩形ABCD中, , ,
∴AB= ,BC=1,
∴AC= =2,
A
∵ ,
∴向量 的长度为2,
故选:A.
3.已知正方形ABCD的边长为1,设 ,那么 的模为( ____ )
A. B. C. D.2
【解析】解:在正方形ABCD中,AB=BC=1,∠B=90°,则由勾股定理,得AC= = .
C
所以 = .
故选:C.
4.如果 是非零向量,那么下列等式正确的是( ____ )
A. = B.| |=| |
C. + =0 D.| |+| |=0
【解析】解:∵ 是非零向量,
∴| |=| |,
故选:B.
B
5.点C是线段AB的中点,则 等于( ____ )
A. B. C.0 D.
【解析】解:∵点C是线段AB的中点,
∴AC=CB.
∴ = .
D
∴ = + = .
故选:D.
6.已知正方形ABCD的边长为1,设 ,那么 的模为( ____ )
A. B.1 C. D.2
【解析】解:在正方形ABCD中,AB=BC=1,∠B=90°,则由勾股定理,得AC= = .
所以 = .
C
故选:C.
7.下列等式中错误的是( ____ )
A. + = B. + = + =
C. +(- )=0 D.( )+ =( )+
【解析】解:A、 + = ,正确.本选项不符合题意;
B、 + = + = ,正确.本选项不符合题意;
C、 + = ,错误,本选项符合题意;
C
D、( + )+ =( + )+ ,正确,本选项不符合题意.
故选:C.
8.已知 , 非零向量,且| + |=| |+| |,则一定有( ____ )
A. = B. ∥ ,且 , 方向相同
C. =- D. ∥ ,且 , 方向相反
【解析】解:∵ , 非零向量,且| + |=| |+| |,
∴平方得| |2+| |2+2 =| |2+| |2+2| | | |,
B
即 =| | | |,
∴| | | |cos< , >=| | | |,
则cos< , >=1,即 ∥ ,且 , 方向相同.
故选:B.
9.在 ABCD中, + 等于( ____ )
A. B. C. D.
【解析】解:在 ABCD中,∵AD∥BC,AD=BC,
∴ = .
∴ + = + = .
B
故选:B.
10.| |= ____ .
【解析】解:| |
=| |
=0.
故答案为:0.
0
11.已知:四边形ABCD,AC与BD交与点O,AO=OC,BO=OD.
求证:四边形ABCD是平行四边形.
A
B
C
D
O
∵AO=OC、BO=OD
得AD∥BC、AD=BC
∴四边形ABCD是平行四边形
证明:作向量AO、OC、BO、OD
又 AO与OC同向、BO与OD同向
∴AO=OC、BO=OD
∵AO+OD=AD, BO+OC=BC
∴AD=BC
课堂小结
1、三角形法则画向量的加法.
2、向量的加法也有交换律和结合律.
3、零向量和零是有区别的.
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 22章 四边形
22.8 平面向量的加法(第1课时)
学习目标
(1)初步掌握向量加法的三角形法则。
(2)学会用作图的方法求两个向量的和向量。
(3)知道向量的加法满足交换律与结合律;并会用它们进行向量的运算。
(4)知道零向量的意义及零向量的特征。
问:长度、面积、体积在确定度量单位后,它们只有大小,可以用一个数来表示.这些量中的同一类量,都可以进行加减运算,而向量不仅有大小,还有方向,两个向量可以相加吗?
这些量称为”数量”又称为“标量”
情景引入
问题1:小明从A地出发向东行走5千米到达B地,再向北又走了5千米到达C地.那么小明这时在A地的什么方向上?到A地的距离是多少?
问1:小明从A地到达B地是不是一次位置移动?从A移动到B的方向是什么?大小又是多少?
是,以A为起点,方向是向东,大小是5千米.
问2:从B地移动到C地是不是又是一次位置移动?方向是什么?大小又是多少?
是,以B为起点,方向是向北,大小是5千米.
根据移动的方向和距离,我们可以把上面的两次移动用向量 和向量 来表示.
如何画有向线段?
(1)定比例尺;(2)取定起点并以它为端点按指定方向画射线;(3)按比例尺截取线段;(4)在线段另一端点画上箭头.
取1:250 000的比例尺,可以画出有向线段来表示向量 和 ,再把起点A和终点C用有向线段连起来,画出有向线段 .
5千米按比例尺截取线段的长度如何计算?
5千米长度如何在纸上表示?
问3:那么这个向量 表示什么?
表示以A为起点,A地到C地的一次位置移动.
问4:如何计算 的大小和方向?
由图可知:△ABC是直角三角形,∠B=90°AB=BC=5(千米),于是可得∠A=45°,AC= (千米),所以,向量 :东北方向,7千米.
从A地到B地,再从B地到C地这两次位置移动合在一起,其结果就是从A地到C地进行了一次位置移动,用向量来表示,就说“向量 与 合在一起是向量 ”,这时称 为 和 的和向量,可表示为 + = .
小明从A地出发向东行走5千米到达B地,再向北又走了5千米到达C地.那么小明这时在A地的什么方向上?A地的距离是多少?
A
B
C
北
东
向东行走5千米
向北行走5千米
定义:求两个向量的和向量的运算叫做向量的加法.
问题2:已知向量 和 ,怎样求这两个向量的和向量?
问:从问题1中我们可以得到启示,当我们把两个位置向量首尾相接时,它们的和向量很容易确定.但是我们如何把这两个向量首尾相接呢?
可以通过平移的方法.
如果 与 是不平行的向量,那么,在平面内任取一点O,作向量 ,使 = ,再作向量 ,以O为起点、B为终点画有向线段 ,则有向线段 所表示的向量 是向量 与向量 的和向量.用算式表示为:
O
B
A
一般来说,求不平行的两个向量的和向量时,只要把第二个向量与第一个向量首尾相接,那么以第一个向量的起点为起点,第二个向量的终点为终点的向量就是和向量.这样的规定叫做向量加法的三角形法则.
起点
第一个向量
终点
和向量的起点
和向量的终点
第二个向量
运用三角形法则的一般步骤:
1、画出表示第一个向量的有向线段;
2、以第一条有向线段的终点作为第二条有向线段的起点(即首尾相接);
3、以第一条有向线段的起点为起点,第二条有向线段的终点为终点画有向线段.
问:如果不作图,你能否直接求出
能,第一条有向线段的终点恰好是第二条有向线段的起点(即首尾相接)
A
A
探究新知
问:如果给出两个平行的向量 和 ,那么如何求他们的和向量?
两个平行向量也可像上面作图一样,此时,向量 、
、 在一条直线上,我们仍规定 .
O A
B
O A
B
∴所求
∴所求
问:当 与 有特殊的关系时,它们的和向量是什么?
当 与 是相等向量时, + = + =2 .
当 与 是互为相反向量时, + = + = .
0
0是向量吗?
互为相反向量的两个向量的和是特殊的向量.
我们把长度为零的向量叫做零向量,记作 .规定 的方向可以是任意的(或者说不确定的); .于是,
问:0和 的区别是什么?
零向量有大小和方向,零只有大小;零向量的模是零.
对于任意的向量,都有 , .
1.两个向量相加,结果一定还是向量;
2.零向量 和实数0的区别在于,零向量不仅表示大小是零,它还有方向,它的方向是任意的.
例题1
如图,已知向量 和 .求作:
(1) (2)
解:(1)在平面内任取一点A,作向量 , ,再作
∴所求 .
A
B
C
例题1
如图,已知向量 和 .求作:
(1) (2)
解:(2)在平面内任取一点D,作向量 , ,再作
∴所求 .
此题运用向量加法的三角形法则.还有其他做法吗?
D
E
F
例题1
如图,已知向量 和 .求作:
(1) (2)
解法2:(2)以AB,BC为邻边,作平行四边形ABCD,再作向量 、 .
∴所求 .
为什么?
∵ABCD是平行四边形,
∴AD//BC,AD=BC;DC//AB;DC=AB.
∴
得
由此我们发现: = ,向量的加法满足交换律.
A
B
C
D
例题2
如图,已知向量 ,求作:
(1) ;
(2)
解:(1)在平面内任取一点O,作向量 , ,得 ;再作 ,然后作向量 ,则
.
请同学先试一试!
(2)作向量 ,得 ,则 .
由此我们发现: ,向量的加法满足结合律.
O
A
B
C
你能先在题1的图形上找到 的和向量吗?
由向量加法的交换律和结合律,可知三个向量相加,运算时可先将其中任意两个向量相加,所得的和向量再与第三个向量相加.
三个向量 、 、 相加,可表示为
.
课本练习
2.如图,已知平行四边形ABCD,在图中作出下列两个向量的和向量.
(1) , ;(2) .
(1)
(2)
∴ 是所求作的向量
如何首尾相接?
∴ 是所求作的向量
运用向量加法的交换律
∴ 是所求作的向量
E
3、填空:
1.下列判断中,不正确的是( ____ )
A. = B. =
C.如果| |=| |,那么 D. +( )=( )
【解析】
解:∵ = , , ,
∴A、B、D正确,
C
随堂检测
∵| |=| |,
∴ 或 ,
故C错误,
故选:C.
2.在矩形ABCD中, , ,则向量 的长度为( ____ )
A.2 B.4 C. D.
【解析】解:在矩形ABCD中, , ,
∴AB= ,BC=1,
∴AC= =2,
A
∵ ,
∴向量 的长度为2,
故选:A.
3.已知正方形ABCD的边长为1,设 ,那么 的模为( ____ )
A. B. C. D.2
【解析】解:在正方形ABCD中,AB=BC=1,∠B=90°,则由勾股定理,得AC= = .
C
所以 = .
故选:C.
4.如果 是非零向量,那么下列等式正确的是( ____ )
A. = B.| |=| |
C. + =0 D.| |+| |=0
【解析】解:∵ 是非零向量,
∴| |=| |,
故选:B.
B
5.点C是线段AB的中点,则 等于( ____ )
A. B. C.0 D.
【解析】解:∵点C是线段AB的中点,
∴AC=CB.
∴ = .
D
∴ = + = .
故选:D.
6.已知正方形ABCD的边长为1,设 ,那么 的模为( ____ )
A. B.1 C. D.2
【解析】解:在正方形ABCD中,AB=BC=1,∠B=90°,则由勾股定理,得AC= = .
所以 = .
C
故选:C.
7.下列等式中错误的是( ____ )
A. + = B. + = + =
C. +(- )=0 D.( )+ =( )+
【解析】解:A、 + = ,正确.本选项不符合题意;
B、 + = + = ,正确.本选项不符合题意;
C、 + = ,错误,本选项符合题意;
C
D、( + )+ =( + )+ ,正确,本选项不符合题意.
故选:C.
8.已知 , 非零向量,且| + |=| |+| |,则一定有( ____ )
A. = B. ∥ ,且 , 方向相同
C. =- D. ∥ ,且 , 方向相反
【解析】解:∵ , 非零向量,且| + |=| |+| |,
∴平方得| |2+| |2+2 =| |2+| |2+2| | | |,
B
即 =| | | |,
∴| | | |cos< , >=| | | |,
则cos< , >=1,即 ∥ ,且 , 方向相同.
故选:B.
9.在 ABCD中, + 等于( ____ )
A. B. C. D.
【解析】解:在 ABCD中,∵AD∥BC,AD=BC,
∴ = .
∴ + = + = .
B
故选:B.
10.| |= ____ .
【解析】解:| |
=| |
=0.
故答案为:0.
0
11.已知:四边形ABCD,AC与BD交与点O,AO=OC,BO=OD.
求证:四边形ABCD是平行四边形.
A
B
C
D
O
∵AO=OC、BO=OD
得AD∥BC、AD=BC
∴四边形ABCD是平行四边形
证明:作向量AO、OC、BO、OD
又 AO与OC同向、BO与OD同向
∴AO=OC、BO=OD
∵AO+OD=AD, BO+OC=BC
∴AD=BC
课堂小结
1、三角形法则画向量的加法.
2、向量的加法也有交换律和结合律.
3、零向量和零是有区别的.
