20.1.1.1平均数和加权平均数(同步课件)-八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 20.1.1.1平均数和加权平均数(同步课件)-八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 32.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第20章
数据的分析
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
20.1.1.1
平均数和
加权平均数
情景引入
李老师想估测从家到学校的路程,先在百米跑道上测试,从起点到终点蹬了22圈.然后记录了10次从家到学校蹬自行车的圈数,结果如下:
427 439 428 438 436 440 432 435 436 439
(1)根据这些数据,估测李老师从家到学校的路程.
情景引入
(2)如果只记录一次蹬自行车的圈数,用这个数据去计算路程,你认为合适吗?为什么要进行多次测量?
解:不合适,误差比较大.进行多次测量取平均值可以减小误差,使估测的结果更准确.
今天我们就共同来研究如何运用平均数来解决实际生活中的一些问题.
平均数
新知探究
一般地,对于n个数x1, x2, …, xn,我们把
叫做这n个数的算术平均数,简称平均数.
典例精析
例1
某次数学考试中,一个学习小组的四位同学A、B、C、D的平均分是80分,为了让该小组成员之间能更好地互帮互学,老师调入E同学,调入后,他们五人本次的平均分变为85分,则E同学本次考试的成绩是
分.
105
解:设E同学本次考试的成绩是x分.
则80×4+x=85×5
解得x=105.
典例精析
例2
某校八年级一班有学生50人,八年级二班有学生45人,期末数学测试中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,这两个班95名学生的平均分是多少?
解:(81.5×50 +83.4×45)÷95
=7828÷95
=82.4
答:这两个班95名学生的平均分是82.4分.
典例精析
例3
某次体操比赛,六位评委对某选手的打分如下(单位:分)9.5,9.3,9.1,9.5,9.4,9.3
(1)求这六个分数的平均分.
(2)如果规定:去掉一个最高分和一个最低分,余下分数的平均值作为选手的最后得分,那么该选手的最后得分是多少?
解:(1)=9.35(分)
答:这六个分数的平均分是9.35分.
(2)=9.375(分)
答:该选手的最后得分是9.375分.
典例精析
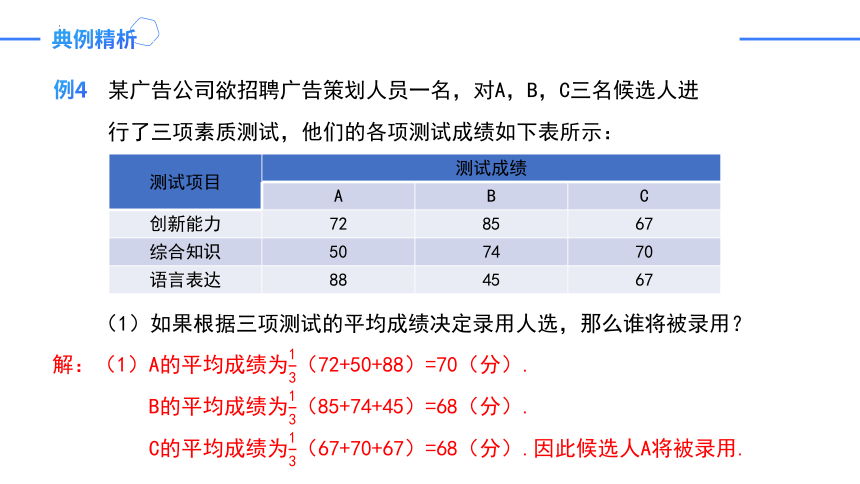
例4
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用?
某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
解:(1)A的平均成绩为(72+50+88)=70(分).
B的平均成绩为(85+74+45)=68(分).
C的平均成绩为(67+70+67)=68(分).因此候选人A将被录用.
测试项目 测试成绩 A B C
创新能力 72 85 67
综合知识 50 74 70
语言表达 88 45 67
典例精析
例4
测试项目 测试成绩 A B C
创新能力 72 85 67
综合知识 50 74 70
语言表达 88 45 67
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4:3:1的比例确定各人测试成绩,此时谁将被录用?
解:(2)A的测试成绩为=65.75(分).
B的测试成绩为=75.875(分).
C的测试成绩为=68.125(分).
因此候选人B将被录用.
典例精析
例4
测试项目 测试成绩 A B C
创新能力 72 85 67
综合知识 50 74 70
语言表达 88 45 67
思考
同样是算平均成绩,为什么会出现不同的结果?
因为测试项目的重要程度不一样!
数据的权能够反映数据的相对重要程度!
同样一张应试者的应聘成绩单,由于各个数据所赋的权数不同,造成的录取结果截然不同.
加权平均数
典例精析
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权.
典例精析
例5
某校规定学生的体育成绩由三部分组成:早锻炼及体育课外活动表现占成绩的20%,体育理论测试占30%,体育技能测试占50%,小颖的上述三项成绩依次是92分、80分、84分,则小颖这学期的体育成绩是多少?
解:小颖这学期的体育成绩是
=84.4(分)
答:小颖这学期的体育成绩是84.4分.
典例精析
例6
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
请决出两人的名次.
选手 演讲内容 演讲能力 演讲效果
A 96 92 95
B 92 90 88
典例精析
例6
选手 演讲内容 演讲能力 演讲效果
A 96 92 88
B 92 90 95
权 50% 40% 10%
解:选手A的最后得分是
选手B的最后得分是
由上可知选手A获得第一名,选手B获得第二名.
归纳总结
平均数与加权平均数
算术平均数:
加权平均数:
当堂检测
1.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A. 255分
B. 84分
C. 84.5分
D. 86分
D
当堂检测
2.一组数据为10,8,9,12,13,10,8,则这组数据的平均数是_________.
3.如果一组数据5,-2,0,6,4,x的平均数是3,那么x等于_____ .
10
5
4.某大桥连续7天的车流量分别为8.0、8.3、9.1、8.5、8.2、8.4、9.0(单位:千辆/日),这七天车流量的平均数为 _____ 千辆/日.
8.5
当堂检测
5.某市9月份30天中的空气污染指数统计如表所示(当w≤50时,空气质量为优;当50<w≤100时,空气质量为良;当100<w≤150时,空气质量为轻微污染)
试计算9月份空气污染的平均指数;再指出这个市在9月份的空气质量属于哪个级别.
解:利用计算器计算,得
所以这个市9月份空气平均污染指数是89.7,空气质量为良.
(w)污染指数 42 45 61 65 72 86 88 90 91
天数 2 1 3 1 1 2 3 1 2
(w)污染指数 93 100 103 104 109 113 115 117 141
天数 2 1 2 1 2 1 1 3 1
当堂检测
6.一家公司打算招聘一名英文翻译,对甲、乙两位应试者进行了听、说、读、写、的英语水平测试,他们的各项成绩如表所示:
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
如果公司想招一名笔译能力较强的翻译, 听、说、读、写的成绩按照2:1:3:4的比确定. 谁能被录用?
因为乙的成绩比甲高,所以应该录取乙.
解: ,
第20章
数据的分析
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
20.1.1.1
平均数和
加权平均数
情景引入
李老师想估测从家到学校的路程,先在百米跑道上测试,从起点到终点蹬了22圈.然后记录了10次从家到学校蹬自行车的圈数,结果如下:
427 439 428 438 436 440 432 435 436 439
(1)根据这些数据,估测李老师从家到学校的路程.
情景引入
(2)如果只记录一次蹬自行车的圈数,用这个数据去计算路程,你认为合适吗?为什么要进行多次测量?
解:不合适,误差比较大.进行多次测量取平均值可以减小误差,使估测的结果更准确.
今天我们就共同来研究如何运用平均数来解决实际生活中的一些问题.
平均数
新知探究
一般地,对于n个数x1, x2, …, xn,我们把
叫做这n个数的算术平均数,简称平均数.
典例精析
例1
某次数学考试中,一个学习小组的四位同学A、B、C、D的平均分是80分,为了让该小组成员之间能更好地互帮互学,老师调入E同学,调入后,他们五人本次的平均分变为85分,则E同学本次考试的成绩是
分.
105
解:设E同学本次考试的成绩是x分.
则80×4+x=85×5
解得x=105.
典例精析
例2
某校八年级一班有学生50人,八年级二班有学生45人,期末数学测试中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,这两个班95名学生的平均分是多少?
解:(81.5×50 +83.4×45)÷95
=7828÷95
=82.4
答:这两个班95名学生的平均分是82.4分.
典例精析
例3
某次体操比赛,六位评委对某选手的打分如下(单位:分)9.5,9.3,9.1,9.5,9.4,9.3
(1)求这六个分数的平均分.
(2)如果规定:去掉一个最高分和一个最低分,余下分数的平均值作为选手的最后得分,那么该选手的最后得分是多少?
解:(1)=9.35(分)
答:这六个分数的平均分是9.35分.
(2)=9.375(分)
答:该选手的最后得分是9.375分.
典例精析
例4
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用?
某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
解:(1)A的平均成绩为(72+50+88)=70(分).
B的平均成绩为(85+74+45)=68(分).
C的平均成绩为(67+70+67)=68(分).因此候选人A将被录用.
测试项目 测试成绩 A B C
创新能力 72 85 67
综合知识 50 74 70
语言表达 88 45 67
典例精析
例4
测试项目 测试成绩 A B C
创新能力 72 85 67
综合知识 50 74 70
语言表达 88 45 67
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4:3:1的比例确定各人测试成绩,此时谁将被录用?
解:(2)A的测试成绩为=65.75(分).
B的测试成绩为=75.875(分).
C的测试成绩为=68.125(分).
因此候选人B将被录用.
典例精析
例4
测试项目 测试成绩 A B C
创新能力 72 85 67
综合知识 50 74 70
语言表达 88 45 67
思考
同样是算平均成绩,为什么会出现不同的结果?
因为测试项目的重要程度不一样!
数据的权能够反映数据的相对重要程度!
同样一张应试者的应聘成绩单,由于各个数据所赋的权数不同,造成的录取结果截然不同.
加权平均数
典例精析
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权.
典例精析
例5
某校规定学生的体育成绩由三部分组成:早锻炼及体育课外活动表现占成绩的20%,体育理论测试占30%,体育技能测试占50%,小颖的上述三项成绩依次是92分、80分、84分,则小颖这学期的体育成绩是多少?
解:小颖这学期的体育成绩是
=84.4(分)
答:小颖这学期的体育成绩是84.4分.
典例精析
例6
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
请决出两人的名次.
选手 演讲内容 演讲能力 演讲效果
A 96 92 95
B 92 90 88
典例精析
例6
选手 演讲内容 演讲能力 演讲效果
A 96 92 88
B 92 90 95
权 50% 40% 10%
解:选手A的最后得分是
选手B的最后得分是
由上可知选手A获得第一名,选手B获得第二名.
归纳总结
平均数与加权平均数
算术平均数:
加权平均数:
当堂检测
1.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
A. 255分
B. 84分
C. 84.5分
D. 86分
D
当堂检测
2.一组数据为10,8,9,12,13,10,8,则这组数据的平均数是_________.
3.如果一组数据5,-2,0,6,4,x的平均数是3,那么x等于_____ .
10
5
4.某大桥连续7天的车流量分别为8.0、8.3、9.1、8.5、8.2、8.4、9.0(单位:千辆/日),这七天车流量的平均数为 _____ 千辆/日.
8.5
当堂检测
5.某市9月份30天中的空气污染指数统计如表所示(当w≤50时,空气质量为优;当50<w≤100时,空气质量为良;当100<w≤150时,空气质量为轻微污染)
试计算9月份空气污染的平均指数;再指出这个市在9月份的空气质量属于哪个级别.
解:利用计算器计算,得
所以这个市9月份空气平均污染指数是89.7,空气质量为良.
(w)污染指数 42 45 61 65 72 86 88 90 91
天数 2 1 3 1 1 2 3 1 2
(w)污染指数 93 100 103 104 109 113 115 117 141
天数 2 1 2 1 2 1 1 3 1
当堂检测
6.一家公司打算招聘一名英文翻译,对甲、乙两位应试者进行了听、说、读、写、的英语水平测试,他们的各项成绩如表所示:
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
如果公司想招一名笔译能力较强的翻译, 听、说、读、写的成绩按照2:1:3:4的比确定. 谁能被录用?
因为乙的成绩比甲高,所以应该录取乙.
解: ,
