第19章一次函数复盘提升(单元复习课件)-八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 第19章一次函数复盘提升(单元复习课件)-八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 38.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 13:54:06 | ||
图片预览






文档简介
(共31张PPT)
第19章
一次函数
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
单元复盘提升
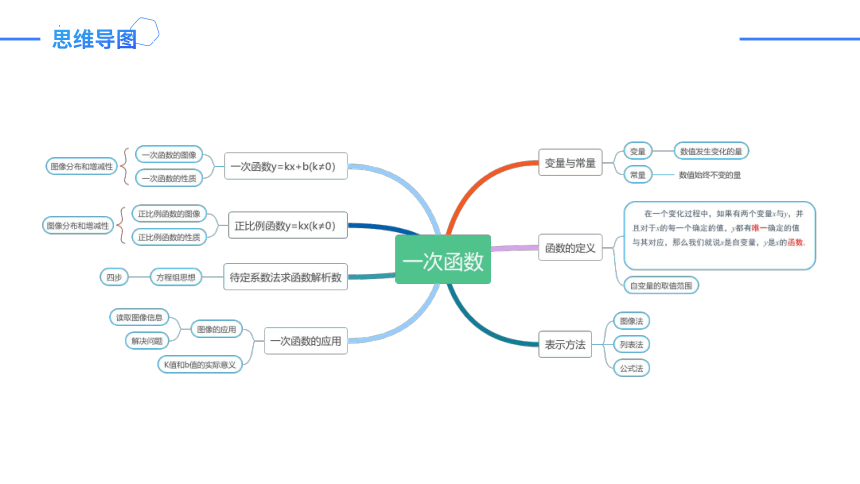
思维导图
知识串讲
1. 常量与变量
叫变量,
叫常量.
数值发生变化的量
数值始终不变的量
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
一、函数
2.函数定义:
知识串讲
3.函数的图象:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法
解析式法
图象法
5.函数的三种表示方法:
4.描点法画图象的步骤:列表、描点、连线
知识串讲
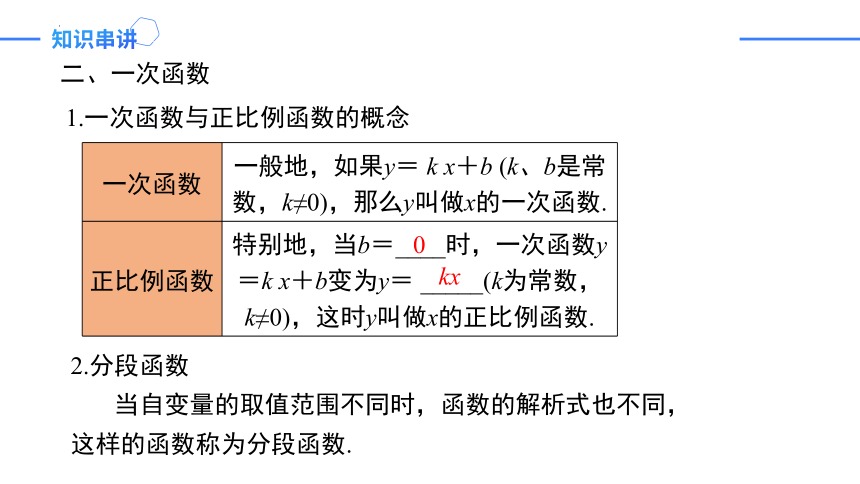
一次函数 一般地,如果y= k x+b (k、b是常数,k≠0),那么y叫做x的一次函数.
正比例函数 特别地,当b=____时,一次函数y=k x+b变为y= _____(k为常数,k≠0),这时y叫做x的正比例函数.
0
kx
二、一次函数
1.一次函数与正比例函数的概念
2.分段函数
当自变量的取值范围不同时,函数的解析式也不同,
这样的函数称为分段函数.
知识串讲
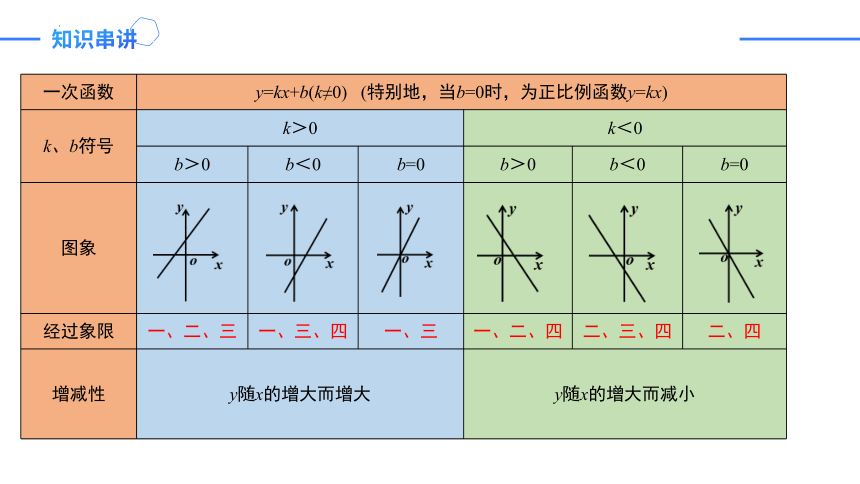
一次函数 y=kx+b(k≠0) (特别地,当b=0时,为正比例函数y=kx) k、b符号 k>0 k<0 b>0 b<0 b=0 b>0 b<0 b=0
图象
经过象限 一、二、三 一、三、四 一、三 一、二、四 二、三、四 二、四
增减性 y随x的增大而增大 y随x的增大而减小 知识串讲
求一次函数解析式的一般步骤:
(1)先设出函数解析式;
(2)根据条件列关于待定系数的方程(组);
(3)解方程(组)求出解析式中未知的系数;
(4)把求出的系数代入设的解析式,从而具体写出这个解析式.这种求解析式的方法叫待定系数法.
4.用待定系数法求一次函数的解析式
知识串讲
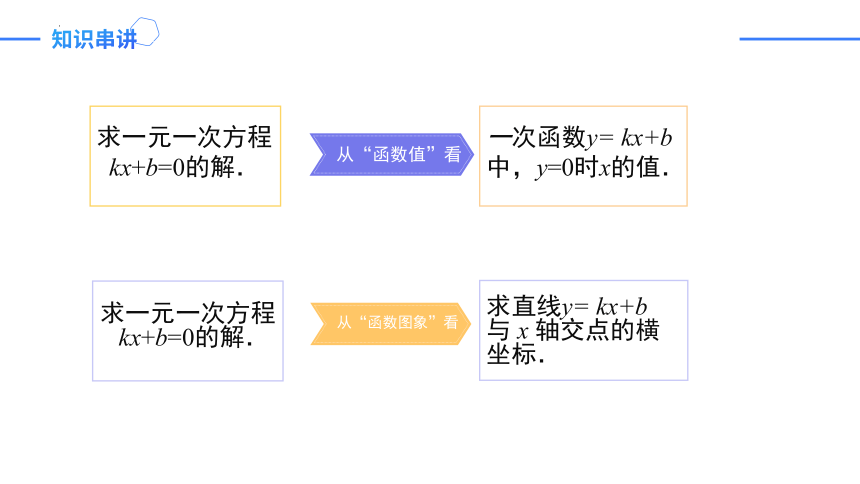
求一元一次方程
kx+b=0的解.
求一元一次方程
kx+b=0的解.
从“函数值”看
添加小标题
从“函数图象”看
一次函数y= kx+b
中,y=0时x的值.
求直线y= kx+b
与 x 轴交点的横
坐标.
知识串讲
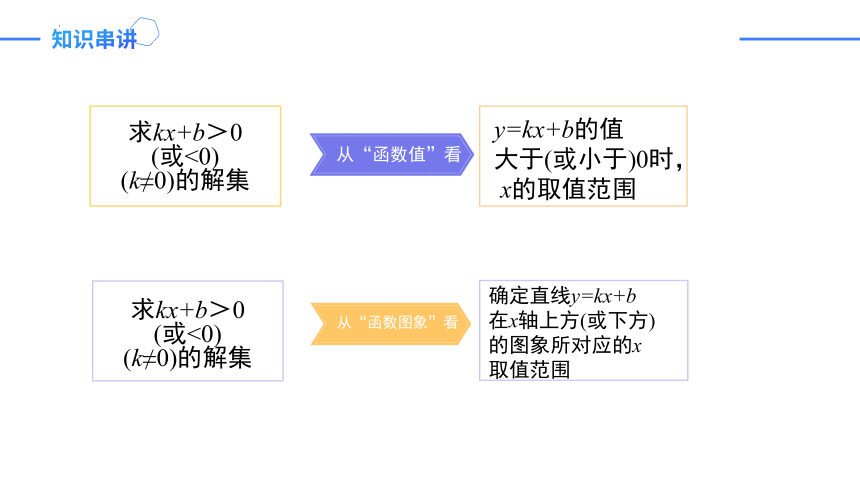
求kx+b>0
(或<0)
(k≠0)的解集
求kx+b>0
(或<0)
(k≠0)的解集
从“函数值”看
添加小标题
从“函数图象”看
y=kx+b的值
大于(或小于)0时,
x的取值范围
确定直线y=kx+b
在x轴上方(或下方)
的图象所对应的x
取值范围
知识串讲
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
方程组的解 对应两条直线交点的坐标.
考点梳理
考点一:函数的有关概念及图象
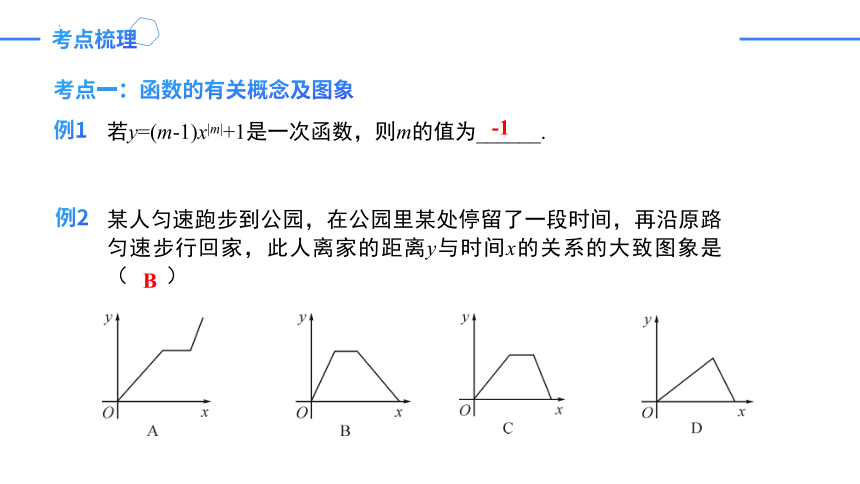
例1
若y=(m-1)x|m|+1是一次函数,则m的值为______.
-1
某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )
B
例2
考点梳理
例3
y是x的正比例函数,当x=2时,y=4,那么当x=-1时,y的值为 ( )
A.2 B.1
C.-2 D.-1
C
例4
正比例函数y=kx的图象如图所示,则k的值为( )
B
刻意练习
练1
在平面直角坐标系中,点M,N在同一个正比例函数图象上的是 ( )
A.M(2,-3),N(-4,6)
B.M(-2,3),N(4,6)
C.M(-2,-3),N(4,-6)
D.M(2,3),N(-4,6)
A
刻意练习
练2
小眀家和学校同处在一条南北向笔直的大道上,他骑单车上学,当骑了一段路时,小明想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与离家距离的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的距离是 米.
(2)小明在书店停留了 分钟.
(3)本次上学途中,小明一共用了 分钟,共骑了 米.
(4)在整个上学的途中 (填具体时间段)小明骑车速度最快,最快的速度 米/分.
(5)观察图象,除上述信息外,你还能得到什么信息?写出一条即可 .
1500
4
14
2700
450
小明家离书店600米
书店离学校900米
分钟
第12到14分钟
考点梳理
考点二:一次函数的图象与性质
例1
(1)正比例函数y=2x的图象经过第_______象限,y随x的增大而______;
(2)已知y=(2m-1)xm -3是正比例函数,且y随x的增大而减小,则m的值是_____.
一、三
增大
-2
如图,三个正比例函数的图象分别对应解析式:
①y=ax;②y=bx;③y=cx.将a,b,c从小到大
排列并用“<”连接为________.
a例2
刻意练习
练1
函数y=3x的图象经过 ( )
A.第一、三象限 B.第二、四象限
C.第一、二象限 D.第三、四象限
A
已知,函数 与在同一坐标系中的大致图象是 ( )
A
B
C
D
C
练2
刻意练习
练3
一次函数y=-5x+2的图象不经过第______象限.
点(-1,y1),(2,y2)是直线y=2x+1上两点,则y1____y2.
三
<
练4
练5
填空:
有下列函数:① , ② ,③ , ④ . 其中函数图象过原点的是_____;
函数y随x的增大而增大的是________;
函数y随x的增大而减小的是_____;
图象在第一、二、三象限的是______.
②
③
①②③
④
x
y
2
=
考点梳理
考点三:一次函数与方程、不等式
例1
一元一次方程 ax-b=0 的解为 x=5,则函数 y=ax-b 与 x 轴的交点坐标是( ).
A.(0,5) B.(0 ,-5)
C
C.(5,0) D.(-5 ,0)
已知一次函数 y=ax+b 与 x 轴、y 轴的交点坐标分别是(-2,0)、(0,4),则关于 x 的不等式 ax+b>0 的解集是( ).
A.x>-2 B. x<-2
A
C.x>4 D.x<4
例2
考点梳理
例3
已知一次函数 y=ax+b 与 y=mx+n 的图象如图所示,那么根据图象可以得出二元一次方程组 的解是________.
x=-1
y=0
(-1,0)
y=ax+b
y=mx+n
x
y
O
刻意练习
练1
用图象法解某二元一次方程组时,在同一直角坐标系中画出相应的两个一次函数的图象,则所解的二元一次方程组是( ).
x+y-2=0
3x-2y-1=0
A.
2x-y-1=0
3x-2y-1=0
B.
2x-y-1=0
3x+2y-5=0
C.
x+y-2=0
2x-y-1=0
D.
D
考点梳理
练2
如图,一次函数y=2x+1的图象与坐标轴分别交于A、B两点,O为坐标原点,则△AOB的面积是( ).
A. B. C. 2 D.4
A
解析:依据题意可知,当x=0时,y=1; y=0时,x=-. 所以A(-,0),B(0,1),则有OA=,OB=1. 则△AOB的面积是.
考点梳理
考点四:一次函数的应用
例1
某家电集团生产某种型号的新家电,前期投资200万元,每生产1台这种新家电,后期还需其他投资0.3万元,已知每台新家电可实现产值0.5万元.
(1)分别求出总投资额y1(万元)和总利润y2(万元)关于新家电的总产量x(台)的函数解析式;
(2)当新家电的总产量为900台时,该公司的盈亏情况如何?
解:(1)根据题意可得: y1=0.3x+200,
y2=0.5x-(0.3x+200)=0.2x-200.
(2)把 x=900 代入 y2=0.2x-200,可得y2=-20<0.
所以当新家电的总产量为 900 台时,公司会亏损,亏损的金额为 20 万元.
考点梳理
考点四:一次函数的应用
例1
某家电集团生产某种型号的新家电,前期投资200万元,每生产1台这种新家电,后期还需其他投资0.3万元,已知每台新家电可实现产值0.5万元.
(3)请你利用(1)中y2和x的函数解析式,分析该公司的盈亏情况.
解:(3)由(1)得 y2=0.2x-200,令 y2<0,解得x<1000.
说明总产量小于1000台时,公司会亏损.
令y2>0,解得x>1000.
说明总产量大于1000台时,公司会盈利.
令y2=0,解得x=1000.
说明总产量等于1000台时,公司既不盈利也不亏损.
考点梳理
例2
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
解:根据图象信息:
货车的速度V货=300÷5=60(千米/时),
由图象可知货车比轿车迟到0.5小时,
∴此时货车距乙地的路程为0.5×60=30(千米);
考点梳理
例2
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,请根据图象解答下列问题:
(2)求线段CD对应的函数解析式.
解:设CD段函数解析式为
y=kx+b(k≠0)(2.5≤x≤4.5).
∵C(2.5,80),D(4.5,300)在其图象上,
∴2.5k+b=80,4.5k+b=300,
解得k=110,b=-195.
∴CD段函数解析式为:
y=110x-195(2.5≤x≤4.5);
考点梳理
例2
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,请根据图象解答下列问题:
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).
解:设轿车从甲地出发x小时后再与货车相遇,
∵v货车=60千米/时,
v轿车=300-804.5-2.5=110(千米/时)
∴110(x-4.5)+60x=300,
解得x≈4.68(小时).
答:轿车从甲地出发约4.68小时后再与货车相遇.
刻意练习
练1
在“美丽家乡,清洁乡村”活动中,李家村村长提出两种购买垃圾桶的方案,方案一:买分类垃圾桶,需要费用 3000 元,以后每月的垃圾处理费用为 250 元;方案二:买不分类垃圾桶,需要费用 1000 元,以后每月的垃圾处理费用为 500 元.设方案一的购买费和垃圾处理费共 y1 元,方案二的购买费和垃圾处理费共 y2 元,交费时间为 x 个月.
(1)直接写出 y1、y2 与 x 的函数解析式;
解:(1) 由题意可得:y1=250x+3000(x≥0);y2=500x+1000(x≥0).
刻意练习
练1
(2)在同一平面直角坐标系中,画出函数 y2、y2 的图象;
(2)对于 y1=250x+3000(x≥0),当 x=0 时,y1=3000;
当 x=4 时,y1=4000 .
过点(0,3000)、(4,4000)在第一象限内画射线,
即是函数 y1=250x+3000(x≥0)的图象.
对于 y2=500x+1000(x≥0) ,当 x=0 时,y2=1000;
当 x=4 时,y1=3000 .
过点(0,1000)、(4,3000)在第一象限内画射线,
即是函数 y2=500x+1000(x≥0)的图象.
刻意练习
练1
y1=250x+3000(x≥0),过点(0,3000)、(4,4000); y2=500x+1000(x≥0),过点(0,1000)、(4,3000).
刻意练习
练1
解得 x=8
y=5000
(3)解方程组 y=250x+3000
y=500x+1000
所以函数 y1=250x+3000(x≥0)、y2=500x+1000(x≥0)的图象的交点坐标为(8,5000).观察图象可得:
当x>8时,y1当x=8时,y1=y2,两种方案费用一样;
当0≤x<8时,y1>y2,方案二更省钱.
(3)在垃圾桶使用寿命相同的情况下,哪种方案更省钱?
第19章
一次函数
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
单元复盘提升
思维导图
知识串讲
1. 常量与变量
叫变量,
叫常量.
数值发生变化的量
数值始终不变的量
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
一、函数
2.函数定义:
知识串讲
3.函数的图象:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法
解析式法
图象法
5.函数的三种表示方法:
4.描点法画图象的步骤:列表、描点、连线
知识串讲
一次函数 一般地,如果y= k x+b (k、b是常数,k≠0),那么y叫做x的一次函数.
正比例函数 特别地,当b=____时,一次函数y=k x+b变为y= _____(k为常数,k≠0),这时y叫做x的正比例函数.
0
kx
二、一次函数
1.一次函数与正比例函数的概念
2.分段函数
当自变量的取值范围不同时,函数的解析式也不同,
这样的函数称为分段函数.
知识串讲
一次函数 y=kx+b(k≠0) (特别地,当b=0时,为正比例函数y=kx) k、b符号 k>0 k<0 b>0 b<0 b=0 b>0 b<0 b=0
图象
经过象限 一、二、三 一、三、四 一、三 一、二、四 二、三、四 二、四
增减性 y随x的增大而增大 y随x的增大而减小 知识串讲
求一次函数解析式的一般步骤:
(1)先设出函数解析式;
(2)根据条件列关于待定系数的方程(组);
(3)解方程(组)求出解析式中未知的系数;
(4)把求出的系数代入设的解析式,从而具体写出这个解析式.这种求解析式的方法叫待定系数法.
4.用待定系数法求一次函数的解析式
知识串讲
求一元一次方程
kx+b=0的解.
求一元一次方程
kx+b=0的解.
从“函数值”看
添加小标题
从“函数图象”看
一次函数y= kx+b
中,y=0时x的值.
求直线y= kx+b
与 x 轴交点的横
坐标.
知识串讲
求kx+b>0
(或<0)
(k≠0)的解集
求kx+b>0
(或<0)
(k≠0)的解集
从“函数值”看
添加小标题
从“函数图象”看
y=kx+b的值
大于(或小于)0时,
x的取值范围
确定直线y=kx+b
在x轴上方(或下方)
的图象所对应的x
取值范围
知识串讲
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
方程组的解 对应两条直线交点的坐标.
考点梳理
考点一:函数的有关概念及图象
例1
若y=(m-1)x|m|+1是一次函数,则m的值为______.
-1
某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )
B
例2
考点梳理
例3
y是x的正比例函数,当x=2时,y=4,那么当x=-1时,y的值为 ( )
A.2 B.1
C.-2 D.-1
C
例4
正比例函数y=kx的图象如图所示,则k的值为( )
B
刻意练习
练1
在平面直角坐标系中,点M,N在同一个正比例函数图象上的是 ( )
A.M(2,-3),N(-4,6)
B.M(-2,3),N(4,6)
C.M(-2,-3),N(4,-6)
D.M(2,3),N(-4,6)
A
刻意练习
练2
小眀家和学校同处在一条南北向笔直的大道上,他骑单车上学,当骑了一段路时,小明想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与离家距离的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的距离是 米.
(2)小明在书店停留了 分钟.
(3)本次上学途中,小明一共用了 分钟,共骑了 米.
(4)在整个上学的途中 (填具体时间段)小明骑车速度最快,最快的速度 米/分.
(5)观察图象,除上述信息外,你还能得到什么信息?写出一条即可 .
1500
4
14
2700
450
小明家离书店600米
书店离学校900米
分钟
第12到14分钟
考点梳理
考点二:一次函数的图象与性质
例1
(1)正比例函数y=2x的图象经过第_______象限,y随x的增大而______;
(2)已知y=(2m-1)xm -3是正比例函数,且y随x的增大而减小,则m的值是_____.
一、三
增大
-2
如图,三个正比例函数的图象分别对应解析式:
①y=ax;②y=bx;③y=cx.将a,b,c从小到大
排列并用“<”连接为________.
a
刻意练习
练1
函数y=3x的图象经过 ( )
A.第一、三象限 B.第二、四象限
C.第一、二象限 D.第三、四象限
A
已知,函数 与在同一坐标系中的大致图象是 ( )
A
B
C
D
C
练2
刻意练习
练3
一次函数y=-5x+2的图象不经过第______象限.
点(-1,y1),(2,y2)是直线y=2x+1上两点,则y1____y2.
三
<
练4
练5
填空:
有下列函数:① , ② ,③ , ④ . 其中函数图象过原点的是_____;
函数y随x的增大而增大的是________;
函数y随x的增大而减小的是_____;
图象在第一、二、三象限的是______.
②
③
①②③
④
x
y
2
=
考点梳理
考点三:一次函数与方程、不等式
例1
一元一次方程 ax-b=0 的解为 x=5,则函数 y=ax-b 与 x 轴的交点坐标是( ).
A.(0,5) B.(0 ,-5)
C
C.(5,0) D.(-5 ,0)
已知一次函数 y=ax+b 与 x 轴、y 轴的交点坐标分别是(-2,0)、(0,4),则关于 x 的不等式 ax+b>0 的解集是( ).
A.x>-2 B. x<-2
A
C.x>4 D.x<4
例2
考点梳理
例3
已知一次函数 y=ax+b 与 y=mx+n 的图象如图所示,那么根据图象可以得出二元一次方程组 的解是________.
x=-1
y=0
(-1,0)
y=ax+b
y=mx+n
x
y
O
刻意练习
练1
用图象法解某二元一次方程组时,在同一直角坐标系中画出相应的两个一次函数的图象,则所解的二元一次方程组是( ).
x+y-2=0
3x-2y-1=0
A.
2x-y-1=0
3x-2y-1=0
B.
2x-y-1=0
3x+2y-5=0
C.
x+y-2=0
2x-y-1=0
D.
D
考点梳理
练2
如图,一次函数y=2x+1的图象与坐标轴分别交于A、B两点,O为坐标原点,则△AOB的面积是( ).
A. B. C. 2 D.4
A
解析:依据题意可知,当x=0时,y=1; y=0时,x=-. 所以A(-,0),B(0,1),则有OA=,OB=1. 则△AOB的面积是.
考点梳理
考点四:一次函数的应用
例1
某家电集团生产某种型号的新家电,前期投资200万元,每生产1台这种新家电,后期还需其他投资0.3万元,已知每台新家电可实现产值0.5万元.
(1)分别求出总投资额y1(万元)和总利润y2(万元)关于新家电的总产量x(台)的函数解析式;
(2)当新家电的总产量为900台时,该公司的盈亏情况如何?
解:(1)根据题意可得: y1=0.3x+200,
y2=0.5x-(0.3x+200)=0.2x-200.
(2)把 x=900 代入 y2=0.2x-200,可得y2=-20<0.
所以当新家电的总产量为 900 台时,公司会亏损,亏损的金额为 20 万元.
考点梳理
考点四:一次函数的应用
例1
某家电集团生产某种型号的新家电,前期投资200万元,每生产1台这种新家电,后期还需其他投资0.3万元,已知每台新家电可实现产值0.5万元.
(3)请你利用(1)中y2和x的函数解析式,分析该公司的盈亏情况.
解:(3)由(1)得 y2=0.2x-200,令 y2<0,解得x<1000.
说明总产量小于1000台时,公司会亏损.
令y2>0,解得x>1000.
说明总产量大于1000台时,公司会盈利.
令y2=0,解得x=1000.
说明总产量等于1000台时,公司既不盈利也不亏损.
考点梳理
例2
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
解:根据图象信息:
货车的速度V货=300÷5=60(千米/时),
由图象可知货车比轿车迟到0.5小时,
∴此时货车距乙地的路程为0.5×60=30(千米);
考点梳理
例2
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,请根据图象解答下列问题:
(2)求线段CD对应的函数解析式.
解:设CD段函数解析式为
y=kx+b(k≠0)(2.5≤x≤4.5).
∵C(2.5,80),D(4.5,300)在其图象上,
∴2.5k+b=80,4.5k+b=300,
解得k=110,b=-195.
∴CD段函数解析式为:
y=110x-195(2.5≤x≤4.5);
考点梳理
例2
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,请根据图象解答下列问题:
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).
解:设轿车从甲地出发x小时后再与货车相遇,
∵v货车=60千米/时,
v轿车=300-804.5-2.5=110(千米/时)
∴110(x-4.5)+60x=300,
解得x≈4.68(小时).
答:轿车从甲地出发约4.68小时后再与货车相遇.
刻意练习
练1
在“美丽家乡,清洁乡村”活动中,李家村村长提出两种购买垃圾桶的方案,方案一:买分类垃圾桶,需要费用 3000 元,以后每月的垃圾处理费用为 250 元;方案二:买不分类垃圾桶,需要费用 1000 元,以后每月的垃圾处理费用为 500 元.设方案一的购买费和垃圾处理费共 y1 元,方案二的购买费和垃圾处理费共 y2 元,交费时间为 x 个月.
(1)直接写出 y1、y2 与 x 的函数解析式;
解:(1) 由题意可得:y1=250x+3000(x≥0);y2=500x+1000(x≥0).
刻意练习
练1
(2)在同一平面直角坐标系中,画出函数 y2、y2 的图象;
(2)对于 y1=250x+3000(x≥0),当 x=0 时,y1=3000;
当 x=4 时,y1=4000 .
过点(0,3000)、(4,4000)在第一象限内画射线,
即是函数 y1=250x+3000(x≥0)的图象.
对于 y2=500x+1000(x≥0) ,当 x=0 时,y2=1000;
当 x=4 时,y1=3000 .
过点(0,1000)、(4,3000)在第一象限内画射线,
即是函数 y2=500x+1000(x≥0)的图象.
刻意练习
练1
y1=250x+3000(x≥0),过点(0,3000)、(4,4000); y2=500x+1000(x≥0),过点(0,1000)、(4,3000).
刻意练习
练1
解得 x=8
y=5000
(3)解方程组 y=250x+3000
y=500x+1000
所以函数 y1=250x+3000(x≥0)、y2=500x+1000(x≥0)的图象的交点坐标为(8,5000).观察图象可得:
当x>8时,y1
当0≤x<8时,y1>y2,方案二更省钱.
(3)在垃圾桶使用寿命相同的情况下,哪种方案更省钱?
