冀教版六年级下册数学第一单元第3课时用正负数表示事物变化课件(共21张PPT)
文档属性
| 名称 | 冀教版六年级下册数学第一单元第3课时用正负数表示事物变化课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
第一单元 第4课时
用正负数表示事物的变化
激趣导入
同学们,今天的数学课我们将进入实验室,测量并记录水的温度。
怎样测量水的温度?
把温度计的玻璃泡完全浸没在水中,等温度计的示数稳定后读出相应的温度。
注意:(1)读数时玻璃泡不能离开水面。
(2)观察者的视线要与温度计中的液柱表面相平。
新知讲解
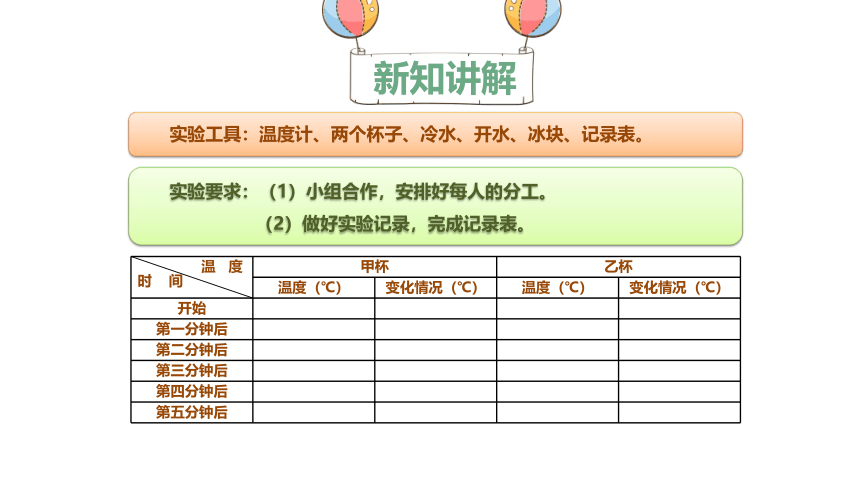
实验工具:温度计、两个杯子、冷水、开水、冰块、记录表。
实验要求:(1)小组合作,安排好每人的分工。
(2)做好实验记录,完成记录表。
温 度时 间 甲杯 乙杯
温度(℃) 变化情况(℃) 温度(℃) 变化情况(℃)
开始
第一分钟后
第二分钟后
第三分钟后
第四分钟后
第五分钟后
新知讲解
实验过程
(1)取两个杯子,各加半杯冷水,分别测量并记录水的温度。
我们组测得的温度是32度。
我们组测得的温度也是32度。
新知讲解
(2)往甲杯中加开水,往乙杯中加冰块。
实验过程
我猜乙杯的温度会低于32度。
我猜甲杯的温度会高于32度
新知讲解
实验过程
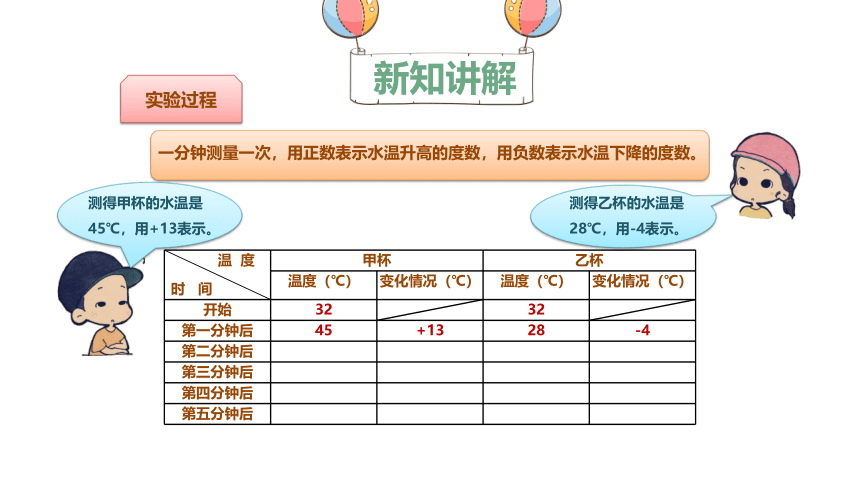
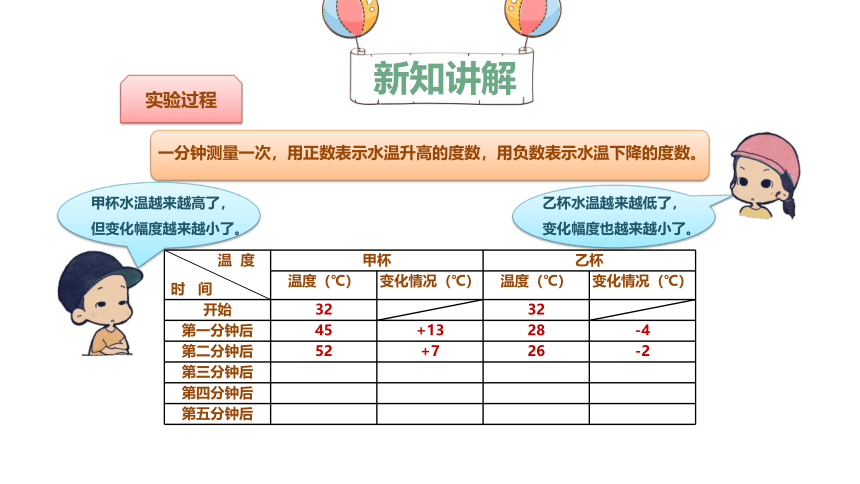
一分钟测量一次,用正数表示水温升高的度数,用负数表示水温下降的度数。
温 度 时 间 甲杯 乙杯
温度(℃) 变化情况(℃) 温度(℃) 变化情况(℃)
开始 32 32
第一分钟后 45 +13 28 -4
第二分钟后
第三分钟后
第四分钟后
第五分钟后
测得乙杯的水温是28℃,用-4表示。
测得甲杯的水温是45℃,用+13表示。
新知讲解
实验过程
一分钟测量一次,用正数表示水温升高的度数,用负数表示水温下降的度数。
温 度 时 间 甲杯 乙杯
温度(℃) 变化情况(℃) 温度(℃) 变化情况(℃)
开始 32 32
第一分钟后 45 +13 28 -4
第二分钟后 52 +7 26 -2
第三分钟后
第四分钟后
第五分钟后
乙杯水温越来越低了,变化幅度也越来越小了。
甲杯水温越来越高了,但变化幅度越来越小了。
新知讲解
实验过程
一分钟测量一次,用正数表示水温升高的度数,用负数表示水温下降的度数。
温 度 时 间 甲杯 乙杯
温度(℃) 变化情况(℃) 温度(℃) 变化情况(℃)
开始 32 32
第一分钟后 45 +13 28 -4
第二分钟后 52 +7 26 -2
第三分钟后 58 +6 25 -1
第四分钟后 60 +2 25 0
第五分钟后 60 0 25 0
乙杯水温到第三分钟时不变了,变化情况为0.
甲杯水温到第四分钟时不变了,变化情况为0。
新知讲解
通过实验,你发现了什么现象?
甲杯的温度越来越高,最后不再变化。代表变化情况的数值为正数,越来越小,最后变成0。
乙杯的温度越来越低,最后不再变化。代表变化情况的数值为负数,越来越大,最后变成0。
新知讲解
1、文文两个月前身高117厘米,文文现在的身高是121厘米,这两个月文文的身高增加了4厘米。
2、早晨气温是8℃,中午上升到12℃,气温上升了4℃。
3、小红的体重是43千克,一个星期后小红的体重是41千克,小红的体重减少了2千克。
4、某路公交车原有12人,到第一站下了若干人,公交车上现在有10人,那么第一站下了2人。
想一想
这四个例子的变化用正负数如何表示呢?
新知讲解
1、文文两个月前身高117厘米,文文现在的身高是121厘米,这两个月文文的身高的变化值是( )。
2、早晨气温是8℃,中午上升到12℃,气温的变化值是( )。
3、小红的体重是43千克,一个星期后小红的体重是41千克,小红的体重的变化值是( )。
4、某路公交车原有12人,到第一站下了若干人,公交车上现在有10人,那么第一站人数变化值是( )。
-2
4
4
-2
这样表示是不是更一目了然呢?
课堂小结
1.用正、负数表示事物的变化时,首先要确定好标准,高于标准的用正数表示,低于标准的用负数表示。
2.用正、负数不仅可以表示水温变化,还可以表示生活中其他一些事物的变化。用正、负数表示事物的变化情况是指在上一次数据的基础上升高或降低的数值。
升降温问题
1.某天早上7时气温是8度,到中午12时上升了4度;从中午到晚上8时下降了2度。中午12时和晚上8时的气温各是多少度?
时间 早上7时 中午12时 晚上8时
变化(℃)
气温(℃)
+4
8
8+4=12
12
-2
12-2=10
10
答:中午12时的气温是12℃,晚上8时的气温是10℃。
2.(1)电梯从1层上升到5层,又从5层下降到1层,然后又上升到3层,再下降到1层,请把这个过程记录在下表中。
(2)电梯从1层上升到6层,然后又下降了2层,现在电梯在几层?
顺序 第一次 第二次 第三次 第四次
移动层数
+4
-4
+2
-2
6-2=4(层)
答:现在电梯在4层。
5-1=4(层)
3-1=2(层)
升降电梯问题
爬行问题
3.蜗牛从10米深的井底往上爬,它每天白天向上爬4米,晚上向下滑2米。想一想:蜗牛第几天可以爬到地面?
第一天 第二天 第三天 第四天
白天 晚上 白天 晚上 白天 晚上 白天
爬行情况 +4米 -2米
+2米
距离井底的高度
4-2+4-2+4-2+4=10(米)
答:第四天可以爬到地面。
+4米 -2米 +4米 -2米 +4米
+2米 +2米 +4米
2米 4米 6米 10米
4.小明从学校门口出发,在学校门口的马路上来回走动,下面是小明记录的自己走动的情况。(假设学校面向南,向东走为正,向西走为负)
走动第五次后,小明在学校门口的什么方向?距离学校门口多少米?
第几次 1 2 3 4 5
走动的情况(米) +100 -25 +115 +65 -275
小明在学校门口正西方向 距学校门口20米
移动问题
出租车司机老王某天上午营运全是在东西走向的解放路上进行,如果规定向东为正,向西为负,他这天上午行车里程(单位:km)如下:
﹢8,﹢4,﹣10,﹣3,﹢6,﹣5,﹣2,﹣7,﹢4,﹢6,﹣9,﹣11。
(1)将第几名乘客送到目的地时,老王刚好回到上午出发点?
(2)将最后一名乘客送到目的地时,老王距上午出发点多远?
(3)若汽车耗油量为0.07L/km,这天上午老王耗油多少升?
(1)第6名;
(2)19km;
(3)5.25L
移动问题
5.下面是几个城市与北京的时差情况统计表。
(1)如果现在北京时间是3月1日上午7:00,那么东京时间是多少?
城市 纽约 巴黎 东京
与北京的时差(时) -13 -7 +1
(2)李叔叔想在北京时间下午3:00给在纽约的弟弟打电话,你认为合适吗?为什么?
时差问题
3月1日7点
2月28日24点
2月28日18点
3月1日8点
0
-7
-13
+1
不合适,此时纽约时间为当日凌晨2点
6.下面是一辆汽车从起点站开出后,途中经过4个停靠站,载客数量的变化情况。
车上原有( )人,中间第一站( )车5人,第2站( )车4人,第3站( )车7人,第4站( )9人,此时车上还剩( )人。
起点站 中间第1站 中间第2站 中间第3站 中间第4站
上下车人数(人) +28 -5 +4 -7 -9
28
上下车问题
下
上
下
下
11
7.某水果超市新进一批水果,每天的售货量和进货量如下(进货为正,售货为负),请你根据表格计算出每天的存货量,并求出最初的进货量(2月24日只有进货)
日期 2月24日 2月25日 2月26日 2月27日 2月28日
进货量和售货量(箱) +15 +18 +22 +10
-20 -25 -25 -12
存货量(箱) 8
倒推法
10
25
20
13
+25
谢谢观看~
第一单元 第4课时
用正负数表示事物的变化
激趣导入
同学们,今天的数学课我们将进入实验室,测量并记录水的温度。
怎样测量水的温度?
把温度计的玻璃泡完全浸没在水中,等温度计的示数稳定后读出相应的温度。
注意:(1)读数时玻璃泡不能离开水面。
(2)观察者的视线要与温度计中的液柱表面相平。
新知讲解
实验工具:温度计、两个杯子、冷水、开水、冰块、记录表。
实验要求:(1)小组合作,安排好每人的分工。
(2)做好实验记录,完成记录表。
温 度时 间 甲杯 乙杯
温度(℃) 变化情况(℃) 温度(℃) 变化情况(℃)
开始
第一分钟后
第二分钟后
第三分钟后
第四分钟后
第五分钟后
新知讲解
实验过程
(1)取两个杯子,各加半杯冷水,分别测量并记录水的温度。
我们组测得的温度是32度。
我们组测得的温度也是32度。
新知讲解
(2)往甲杯中加开水,往乙杯中加冰块。
实验过程
我猜乙杯的温度会低于32度。
我猜甲杯的温度会高于32度
新知讲解
实验过程
一分钟测量一次,用正数表示水温升高的度数,用负数表示水温下降的度数。
温 度 时 间 甲杯 乙杯
温度(℃) 变化情况(℃) 温度(℃) 变化情况(℃)
开始 32 32
第一分钟后 45 +13 28 -4
第二分钟后
第三分钟后
第四分钟后
第五分钟后
测得乙杯的水温是28℃,用-4表示。
测得甲杯的水温是45℃,用+13表示。
新知讲解
实验过程
一分钟测量一次,用正数表示水温升高的度数,用负数表示水温下降的度数。
温 度 时 间 甲杯 乙杯
温度(℃) 变化情况(℃) 温度(℃) 变化情况(℃)
开始 32 32
第一分钟后 45 +13 28 -4
第二分钟后 52 +7 26 -2
第三分钟后
第四分钟后
第五分钟后
乙杯水温越来越低了,变化幅度也越来越小了。
甲杯水温越来越高了,但变化幅度越来越小了。
新知讲解
实验过程
一分钟测量一次,用正数表示水温升高的度数,用负数表示水温下降的度数。
温 度 时 间 甲杯 乙杯
温度(℃) 变化情况(℃) 温度(℃) 变化情况(℃)
开始 32 32
第一分钟后 45 +13 28 -4
第二分钟后 52 +7 26 -2
第三分钟后 58 +6 25 -1
第四分钟后 60 +2 25 0
第五分钟后 60 0 25 0
乙杯水温到第三分钟时不变了,变化情况为0.
甲杯水温到第四分钟时不变了,变化情况为0。
新知讲解
通过实验,你发现了什么现象?
甲杯的温度越来越高,最后不再变化。代表变化情况的数值为正数,越来越小,最后变成0。
乙杯的温度越来越低,最后不再变化。代表变化情况的数值为负数,越来越大,最后变成0。
新知讲解
1、文文两个月前身高117厘米,文文现在的身高是121厘米,这两个月文文的身高增加了4厘米。
2、早晨气温是8℃,中午上升到12℃,气温上升了4℃。
3、小红的体重是43千克,一个星期后小红的体重是41千克,小红的体重减少了2千克。
4、某路公交车原有12人,到第一站下了若干人,公交车上现在有10人,那么第一站下了2人。
想一想
这四个例子的变化用正负数如何表示呢?
新知讲解
1、文文两个月前身高117厘米,文文现在的身高是121厘米,这两个月文文的身高的变化值是( )。
2、早晨气温是8℃,中午上升到12℃,气温的变化值是( )。
3、小红的体重是43千克,一个星期后小红的体重是41千克,小红的体重的变化值是( )。
4、某路公交车原有12人,到第一站下了若干人,公交车上现在有10人,那么第一站人数变化值是( )。
-2
4
4
-2
这样表示是不是更一目了然呢?
课堂小结
1.用正、负数表示事物的变化时,首先要确定好标准,高于标准的用正数表示,低于标准的用负数表示。
2.用正、负数不仅可以表示水温变化,还可以表示生活中其他一些事物的变化。用正、负数表示事物的变化情况是指在上一次数据的基础上升高或降低的数值。
升降温问题
1.某天早上7时气温是8度,到中午12时上升了4度;从中午到晚上8时下降了2度。中午12时和晚上8时的气温各是多少度?
时间 早上7时 中午12时 晚上8时
变化(℃)
气温(℃)
+4
8
8+4=12
12
-2
12-2=10
10
答:中午12时的气温是12℃,晚上8时的气温是10℃。
2.(1)电梯从1层上升到5层,又从5层下降到1层,然后又上升到3层,再下降到1层,请把这个过程记录在下表中。
(2)电梯从1层上升到6层,然后又下降了2层,现在电梯在几层?
顺序 第一次 第二次 第三次 第四次
移动层数
+4
-4
+2
-2
6-2=4(层)
答:现在电梯在4层。
5-1=4(层)
3-1=2(层)
升降电梯问题
爬行问题
3.蜗牛从10米深的井底往上爬,它每天白天向上爬4米,晚上向下滑2米。想一想:蜗牛第几天可以爬到地面?
第一天 第二天 第三天 第四天
白天 晚上 白天 晚上 白天 晚上 白天
爬行情况 +4米 -2米
+2米
距离井底的高度
4-2+4-2+4-2+4=10(米)
答:第四天可以爬到地面。
+4米 -2米 +4米 -2米 +4米
+2米 +2米 +4米
2米 4米 6米 10米
4.小明从学校门口出发,在学校门口的马路上来回走动,下面是小明记录的自己走动的情况。(假设学校面向南,向东走为正,向西走为负)
走动第五次后,小明在学校门口的什么方向?距离学校门口多少米?
第几次 1 2 3 4 5
走动的情况(米) +100 -25 +115 +65 -275
小明在学校门口正西方向 距学校门口20米
移动问题
出租车司机老王某天上午营运全是在东西走向的解放路上进行,如果规定向东为正,向西为负,他这天上午行车里程(单位:km)如下:
﹢8,﹢4,﹣10,﹣3,﹢6,﹣5,﹣2,﹣7,﹢4,﹢6,﹣9,﹣11。
(1)将第几名乘客送到目的地时,老王刚好回到上午出发点?
(2)将最后一名乘客送到目的地时,老王距上午出发点多远?
(3)若汽车耗油量为0.07L/km,这天上午老王耗油多少升?
(1)第6名;
(2)19km;
(3)5.25L
移动问题
5.下面是几个城市与北京的时差情况统计表。
(1)如果现在北京时间是3月1日上午7:00,那么东京时间是多少?
城市 纽约 巴黎 东京
与北京的时差(时) -13 -7 +1
(2)李叔叔想在北京时间下午3:00给在纽约的弟弟打电话,你认为合适吗?为什么?
时差问题
3月1日7点
2月28日24点
2月28日18点
3月1日8点
0
-7
-13
+1
不合适,此时纽约时间为当日凌晨2点
6.下面是一辆汽车从起点站开出后,途中经过4个停靠站,载客数量的变化情况。
车上原有( )人,中间第一站( )车5人,第2站( )车4人,第3站( )车7人,第4站( )9人,此时车上还剩( )人。
起点站 中间第1站 中间第2站 中间第3站 中间第4站
上下车人数(人) +28 -5 +4 -7 -9
28
上下车问题
下
上
下
下
11
7.某水果超市新进一批水果,每天的售货量和进货量如下(进货为正,售货为负),请你根据表格计算出每天的存货量,并求出最初的进货量(2月24日只有进货)
日期 2月24日 2月25日 2月26日 2月27日 2月28日
进货量和售货量(箱) +15 +18 +22 +10
-20 -25 -25 -12
存货量(箱) 8
倒推法
10
25
20
13
+25
谢谢观看~
