初中数学人教版八年级下册17.2 勾股定理的逆定理 课件(24张PPT)
文档属性
| 名称 | 初中数学人教版八年级下册17.2 勾股定理的逆定理 课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 00:00:00 | ||
图片预览


文档简介
(共24张PPT)
17.2 勾股定理的逆定理
年 级:八年级
学 科:初中数学(人教版)
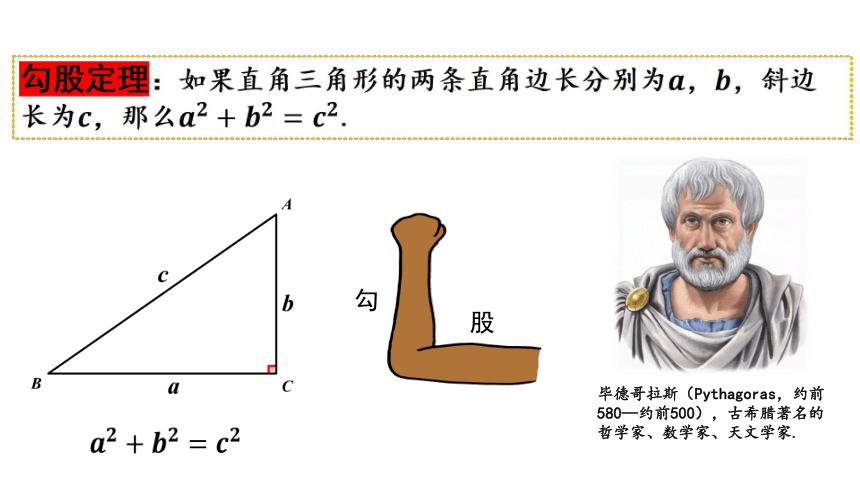
勾
股
勾股定理:如果直角三角形的两条直角边长分别为,,斜边长为,那么.
毕德哥拉斯(Pythagoras,约前580—约前500),古希腊著名的哲学家、数学家、天文学家.
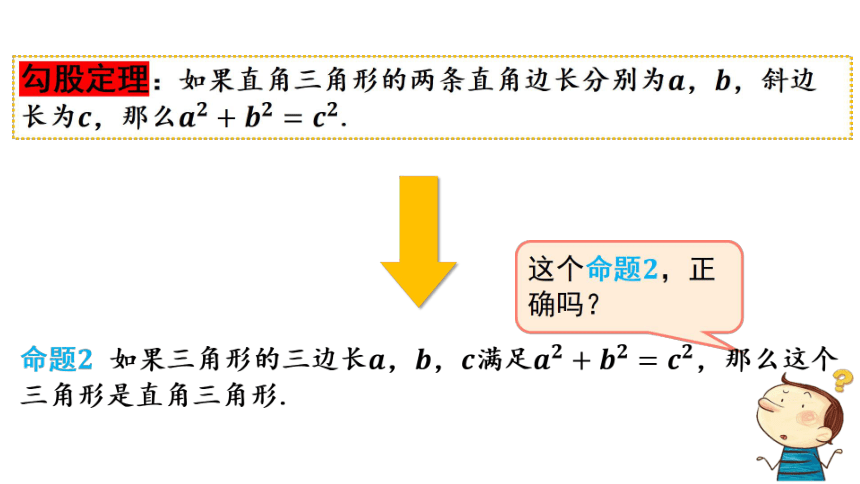
这个命题,正确吗?
勾股定理:如果直角三角形的两条直角边长分别为,,斜边长为,那么.
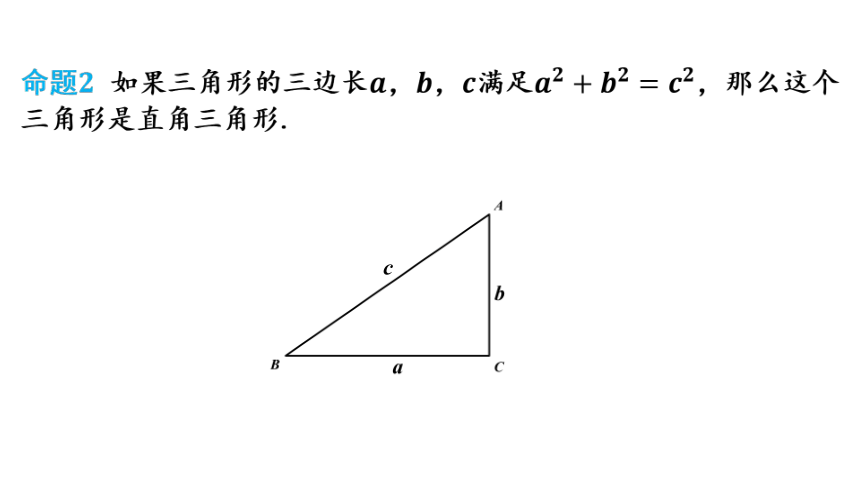
命题 如果三角形的三边长,,满足,那么这个三角形是直角三角形.
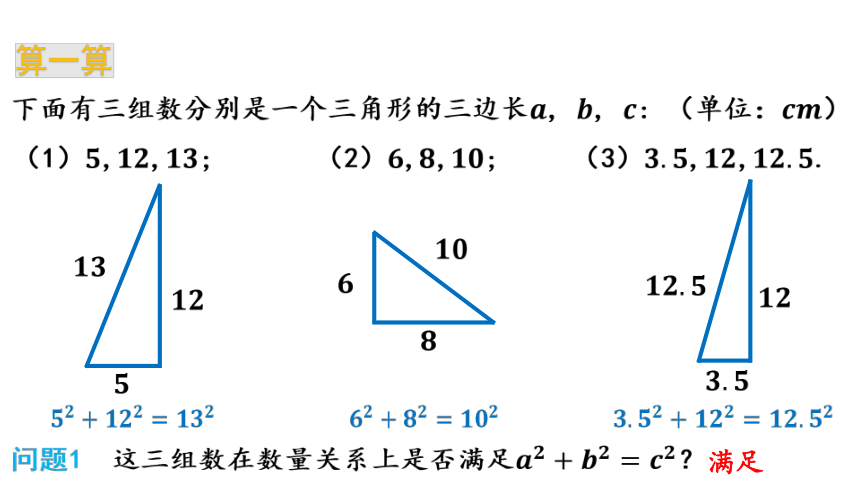
算一算
下面有三组数分别是一个三角形的三边长, , : (单位:)
(1),,; (2),,; (3),,.
问题1 这三组数在数量关系上是否满足?
满足
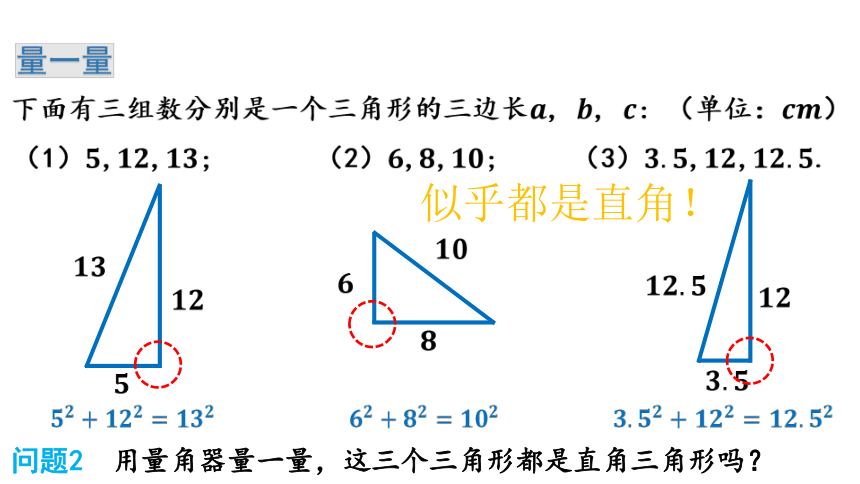
量一量
下面有三组数分别是一个三角形的三边长, , : (单位:)
(1),,; (2),,; (3),,.
问题2 用量角器量一量,这三个三角形都是直角三角形吗?
似乎都是直角!
这个命题,正确吗?
勾股定理:如果直角三角形的两条直角边长分别为,,斜边长为,那么.
命题 如果三角形的三边长,,满足,那么这个三角形是直角三角形.
命题 如果三角形的三边长,,满足,那么这个三角形是直角三角形.
命题 如果三角形的三边长,,满足,那么这个三角形是直角三角形.
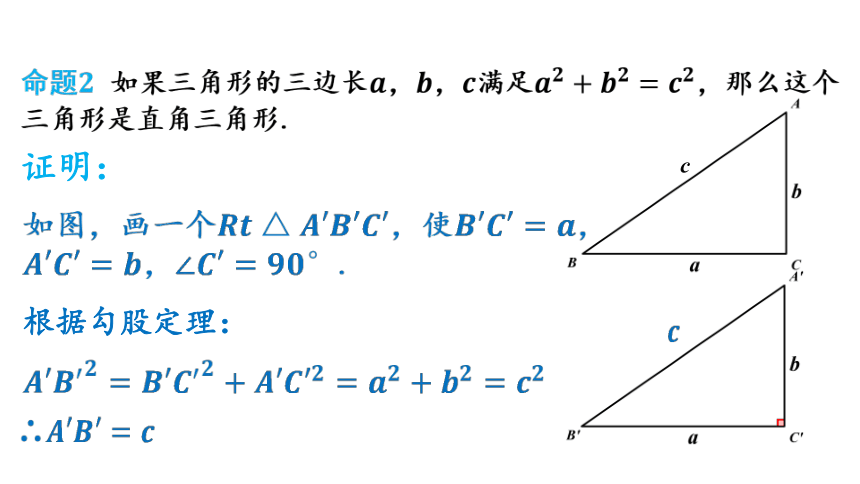
证明:
如图,画一个,使,,.
根据勾股定理:
∴
命题 如果三角形的三边长,,满足,那么这个三角形是直角三角形.
证明:
在和中,
∴≌(SSS)
∴
即.
真命题
勾股定理逆定理:如果三角形的三边长 , , ,满足
,那么这个三角形是直角三角形.
几何语言——勾股定理逆定理:
∵
∴ .
是直角三角形
例1 判断由线段,,组成的三角形是不是直角三角形.
(1) ,,;
(2) ,,.
解:
(1)∵
(2)∴
(2)∴
(3)∴这个三角形是直角三角形.
(2)∵
(2)∴
(2)∴
(3)∴这个三角形不是直角三角形.
(2)∵
练1 判断由线段,,组成的三角形是不是直角三角形.
(1),,;
(2),,;
(3),,;
(4),,.
练1 判断由线段,,组成的三角形是不是直角三角形.
(1),,;
(1)∵
(2)∴
(2)∴
(3)∴这个三角形是直角三角形.
解:
练1 判断由线段,,组成的三角形是不是直角三角形.
(2),,;
(2)∵
(2)∴
(2)∴
(3)∴这个三角形是直角三角形.
练1 判断由线段,,组成的三角形是不是直角三角形.
(3),,;
(3)∵
(2)∴
(2)∴
(3)∴这个三角形是直角三角形.
练1 判断由线段,,组成的三角形是不是直角三角形.
(4),,.
(4)∵
(2)∴
(2)∴
(3)∴这个三角形不是直角三角形.
练1 判断由线段,,组成的三角形是不是直角三角形.
(4),,.
(4)∵
(2)∴
(2)∴
(3)∴这个三角形不是直角三角形.
例2 如图,某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行,“海天”号每小时航行.它们离开港口一个半小时后分别位于点,处,且相距.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
解:
∵
即
∴
由“远航”号沿东北方向航行可知,.
因此,即“海天”号沿西北方向航行.
练2 如图所示,甲、乙两船从港口同时出发,甲船以海里/时的速度向北偏东的方向航行,乙船以海里/时的速度向另一方向航行,小时后,甲船到达岛,乙船到达岛,若,两岛相距海里,则乙船航行的角度是南偏东多少度
解:
(海里)
(海里)
(海里)
∵
即
解:
(海里)
(海里)
(海里)
∵
即
∴
答:乙船航行的角度是南偏东度.
拓1-1 下列各组线段中,能构成直角三角形的是( )
拓1-2 若的三边,,满足,则是_______________________.
等腰直角三角形
【解析】.选.
【解析】由题意,得
∴
即 是等腰直角三角形.
拓2 如图,在四边形中,,,
,,.求四边形的面积.
解:
∵,
∵
∴
即
∵,
即
∴
∴△ACD
∴四边形ABCD
小 结
17.2 勾股定理的逆定理
年 级:八年级
学 科:初中数学(人教版)
勾
股
勾股定理:如果直角三角形的两条直角边长分别为,,斜边长为,那么.
毕德哥拉斯(Pythagoras,约前580—约前500),古希腊著名的哲学家、数学家、天文学家.
这个命题,正确吗?
勾股定理:如果直角三角形的两条直角边长分别为,,斜边长为,那么.
命题 如果三角形的三边长,,满足,那么这个三角形是直角三角形.
算一算
下面有三组数分别是一个三角形的三边长, , : (单位:)
(1),,; (2),,; (3),,.
问题1 这三组数在数量关系上是否满足?
满足
量一量
下面有三组数分别是一个三角形的三边长, , : (单位:)
(1),,; (2),,; (3),,.
问题2 用量角器量一量,这三个三角形都是直角三角形吗?
似乎都是直角!
这个命题,正确吗?
勾股定理:如果直角三角形的两条直角边长分别为,,斜边长为,那么.
命题 如果三角形的三边长,,满足,那么这个三角形是直角三角形.
命题 如果三角形的三边长,,满足,那么这个三角形是直角三角形.
命题 如果三角形的三边长,,满足,那么这个三角形是直角三角形.
证明:
如图,画一个,使,,.
根据勾股定理:
∴
命题 如果三角形的三边长,,满足,那么这个三角形是直角三角形.
证明:
在和中,
∴≌(SSS)
∴
即.
真命题
勾股定理逆定理:如果三角形的三边长 , , ,满足
,那么这个三角形是直角三角形.
几何语言——勾股定理逆定理:
∵
∴ .
是直角三角形
例1 判断由线段,,组成的三角形是不是直角三角形.
(1) ,,;
(2) ,,.
解:
(1)∵
(2)∴
(2)∴
(3)∴这个三角形是直角三角形.
(2)∵
(2)∴
(2)∴
(3)∴这个三角形不是直角三角形.
(2)∵
练1 判断由线段,,组成的三角形是不是直角三角形.
(1),,;
(2),,;
(3),,;
(4),,.
练1 判断由线段,,组成的三角形是不是直角三角形.
(1),,;
(1)∵
(2)∴
(2)∴
(3)∴这个三角形是直角三角形.
解:
练1 判断由线段,,组成的三角形是不是直角三角形.
(2),,;
(2)∵
(2)∴
(2)∴
(3)∴这个三角形是直角三角形.
练1 判断由线段,,组成的三角形是不是直角三角形.
(3),,;
(3)∵
(2)∴
(2)∴
(3)∴这个三角形是直角三角形.
练1 判断由线段,,组成的三角形是不是直角三角形.
(4),,.
(4)∵
(2)∴
(2)∴
(3)∴这个三角形不是直角三角形.
练1 判断由线段,,组成的三角形是不是直角三角形.
(4),,.
(4)∵
(2)∴
(2)∴
(3)∴这个三角形不是直角三角形.
例2 如图,某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行,“海天”号每小时航行.它们离开港口一个半小时后分别位于点,处,且相距.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
解:
∵
即
∴
由“远航”号沿东北方向航行可知,.
因此,即“海天”号沿西北方向航行.
练2 如图所示,甲、乙两船从港口同时出发,甲船以海里/时的速度向北偏东的方向航行,乙船以海里/时的速度向另一方向航行,小时后,甲船到达岛,乙船到达岛,若,两岛相距海里,则乙船航行的角度是南偏东多少度
解:
(海里)
(海里)
(海里)
∵
即
解:
(海里)
(海里)
(海里)
∵
即
∴
答:乙船航行的角度是南偏东度.
拓1-1 下列各组线段中,能构成直角三角形的是( )
拓1-2 若的三边,,满足,则是_______________________.
等腰直角三角形
【解析】.选.
【解析】由题意,得
∴
即 是等腰直角三角形.
拓2 如图,在四边形中,,,
,,.求四边形的面积.
解:
∵,
∵
∴
即
∵,
即
∴
∴△ACD
∴四边形ABCD
小 结
