人教版八年级下册19.2 一次函数与二元一次方程组 课件(14张PPT)
文档属性
| 名称 | 人教版八年级下册19.2 一次函数与二元一次方程组 课件(14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 288.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 14:12:46 | ||
图片预览





文档简介
(共14张PPT)
一次函数与二元一次方程组
年 级:八年级
学 科:初中数学(人教版)
问题1: 1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号气球从海拔15m处出发,以0.5m/min的速度上升.两气球都上升了1h. 请用解析式分别表示两个气球所在位置的海拔y(单位:m)与上升时间为x(单位:min)的函数关系.
创设情境 提出问题
1号气球:函数解析式为y=x+5
2号气球:函数解析式为y=0.5x+15
一次函数的表达式是一个二元一次方程
思考:如果把x,y看作未知数,那么这两个式子表示什么意义?
用方程的观点看一次函数
请先按暂停键!思考完成后
再按回播放键!
数
观察思考 探究新知
问题2:写三个一次函数,用方程的观点看式子,有什么发现?再写三个二元一次方程,如果把未知数看作变量,变量之间的关系是什么?
思考:如果从形的观点看,它们之间有什么联系?
一次函数 y=0.5x+15
一次函数 y=x+5
一次函数 y=-2x+7
二元一次方程 x-y=-5
二元一次方程 0.5x-y=-15
二元一次方程 2x+y=7
用方程观点看
用函数观点看
……
……
请先按暂停键!思考完成后
再按回播放键!
观察思考 探究新知
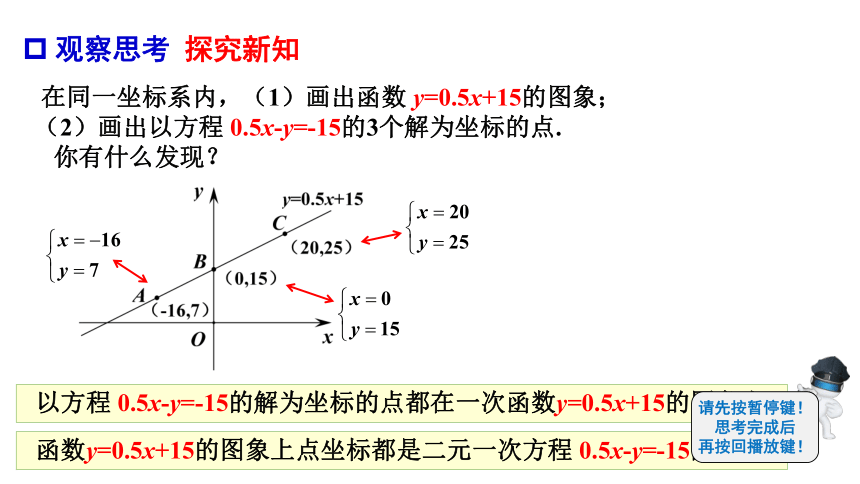
在同一坐标系内,(1)画出函数 y=0.5x+15的图象;
(2)画出以方程 0.5x-y=-15的3个解为坐标的点.
你有什么发现?
以方程 0.5x-y=-15的解为坐标的点都在一次函数y=0.5x+15的图象上,
函数y=0.5x+15的图象上点坐标都是二元一次方程 0.5x-y=-15的解.
请先按暂停键!思考完成后
再按回播放键!
观察思考 探究新知
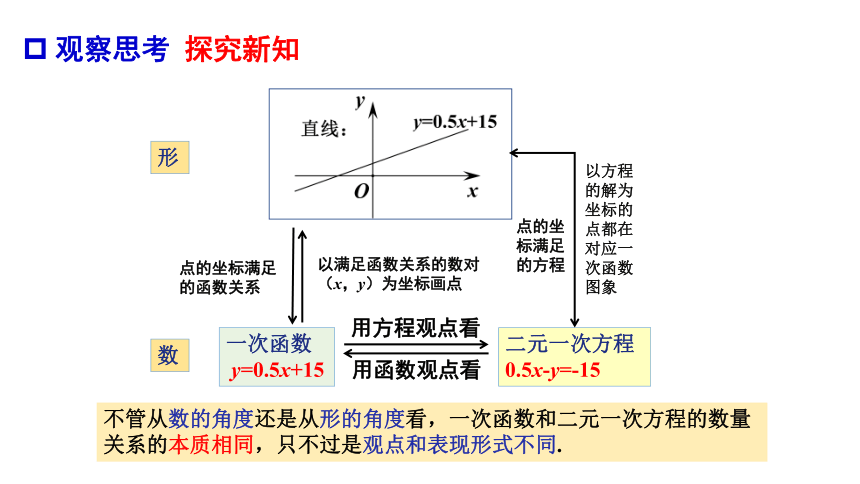
不管从数的角度还是从形的角度看,一次函数和二元一次方程的数量关系的本质相同,只不过是观点和表现形式不同.
一次函数
y=0.5x+15
二元一次方程
0.5x-y=-15
用方程观点看
用函数观点看
形
数
点的坐标满足 的函数关系
以满足函数关系的数对(x,y)为坐标画点
点的坐标满足 的方程
以方程 的解为坐标的点都在对应一次函数图象
问题3:由于两个气球上升的速度不同,开始时2号气球高,1号气球低,那么永远如此吗?什么时刻1号气球的高度赶上2号气球的高度?你会从数和形两方面分别加以研究吗?
(1)从数量关系的角度研究
当两个气球高度相同时,时间x与高度y同时满足这两个方程,也就是它们组成的方程组的解.
1号气球高度与时间的关系为:y=x+5
2号气球高度与时间的关系为:y=0.5x+15
y=x+5,
y=0.5x+15,
解方程组 得
x=20,
y=25.
因此气球上升20min时,
它们的高度相同,都是25m.
观察思考 探究新知
请先按暂停键!思考完成后
再按回播放键!
问题3:由于两个气球上升的速度不同,开始时2号气球高,1号气球低,那么永远如此吗?什么时刻1号气球的高度赶上2号气球的高度?你会从数和形两方面分别加以研究吗?
(2)从图形的角度研究
在同一坐标系中画出两个函数的图象,如图,
观察思考 探究新知
从中发现,当x=20时,对应的函数值相等,都是25.也就是说,两直线交于一点,交点坐标为(20,25).
请先按暂停键!思考完成后
再按回播放键!
回顾上面的解题过程,用函数观点看方程组
你得到哪些结论?你能把得到的结论推广到一般情况吗?
从“形”的角度看,解二元一次方程组相当于确定两条相应直线交点坐标.
总结:每个二元一次方程组都对应两个一次函数, 于是也对应两条直线.
从“数”的角度看,解二元一次方程组相当于求自变量为何值时,相应的两个函数值相等.
观察思考 探究新知
练习巩固 内化新知
1.若方程组 的解为 则一次函数y=2x+1与y=3x-1的图象交点坐标为________.
(2,5)
解:方程2x-y=-1可化为y=2x+1,
方程3x-y=1可化为y=3x-1,
∴方程组的解分别为对应两条直线交点的横纵坐标,
∴图象交点为(2,5)
请先按暂停键!思考完成后
再按回播放键!
练习巩固 内化新知
2.一次函数 y1= 4x + 5 与 y2 = 3x + 10 的图象如图所示,
则方程组 的解为?
O
x
y
5
y = 4x + 5
y = 3x + 10
25
解:方程4x-y=5可化为y=4x+5,
方程3x-y=-10可化为y=3x+10,
∴两条直线交点的横纵坐标,分别为对应方程组解的x,y的值,
∴方程组的解为
请先按暂停键!思考完成后
再按回播放键!
3.如图,直线 l1∶y=x+1与直线 l2∶y=mx+n 相交于点P (1,b).
(1)求b 的值.
(2)不解关于x,y 的方程组
请你直接写出它的解.
(3)直线 l3∶y=nx+m 是否也经过点P?
请说明理由.
练习巩固 内化新知
请先按暂停键!思考完成后
再按回播放键!
练习巩固 内化新知
解:(1)把P (1,b)的坐标代入 y=x+1得b=2.
(2)由(1)得P (1,2),
∴方程组 的解为
(3)直线l3∶y=nx+m 经过点P. 理由如下:
∵直线y=mx+n 经过点P (1,2),
∴m+n=2,
而把点P (1,2)代入y=nx+m也得到 m+n=2
∴直线 y=nx+m 也经过P 点.
一次函数
y=0.5x+15
二元一次方程
0.5x-y=-15
用方程观点看
用函数观点看
形
数
点的坐标满足 的函数关系
以满足函数关系的数对(x,y)为坐标画点
点的坐标满足 的方程
y=x+5
y=0.5x+15
解方程组
求自变量为何值时,相应的两个函数值相等
确定两条相应直线交点坐标
小结梳理 形成体系
以方程 的解为坐标的点都在对应一次函数图象
同学们,再见
一次函数与二元一次方程组
年 级:八年级
学 科:初中数学(人教版)
问题1: 1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号气球从海拔15m处出发,以0.5m/min的速度上升.两气球都上升了1h. 请用解析式分别表示两个气球所在位置的海拔y(单位:m)与上升时间为x(单位:min)的函数关系.
创设情境 提出问题
1号气球:函数解析式为y=x+5
2号气球:函数解析式为y=0.5x+15
一次函数的表达式是一个二元一次方程
思考:如果把x,y看作未知数,那么这两个式子表示什么意义?
用方程的观点看一次函数
请先按暂停键!思考完成后
再按回播放键!
数
观察思考 探究新知
问题2:写三个一次函数,用方程的观点看式子,有什么发现?再写三个二元一次方程,如果把未知数看作变量,变量之间的关系是什么?
思考:如果从形的观点看,它们之间有什么联系?
一次函数 y=0.5x+15
一次函数 y=x+5
一次函数 y=-2x+7
二元一次方程 x-y=-5
二元一次方程 0.5x-y=-15
二元一次方程 2x+y=7
用方程观点看
用函数观点看
……
……
请先按暂停键!思考完成后
再按回播放键!
观察思考 探究新知
在同一坐标系内,(1)画出函数 y=0.5x+15的图象;
(2)画出以方程 0.5x-y=-15的3个解为坐标的点.
你有什么发现?
以方程 0.5x-y=-15的解为坐标的点都在一次函数y=0.5x+15的图象上,
函数y=0.5x+15的图象上点坐标都是二元一次方程 0.5x-y=-15的解.
请先按暂停键!思考完成后
再按回播放键!
观察思考 探究新知
不管从数的角度还是从形的角度看,一次函数和二元一次方程的数量关系的本质相同,只不过是观点和表现形式不同.
一次函数
y=0.5x+15
二元一次方程
0.5x-y=-15
用方程观点看
用函数观点看
形
数
点的坐标满足 的函数关系
以满足函数关系的数对(x,y)为坐标画点
点的坐标满足 的方程
以方程 的解为坐标的点都在对应一次函数图象
问题3:由于两个气球上升的速度不同,开始时2号气球高,1号气球低,那么永远如此吗?什么时刻1号气球的高度赶上2号气球的高度?你会从数和形两方面分别加以研究吗?
(1)从数量关系的角度研究
当两个气球高度相同时,时间x与高度y同时满足这两个方程,也就是它们组成的方程组的解.
1号气球高度与时间的关系为:y=x+5
2号气球高度与时间的关系为:y=0.5x+15
y=x+5,
y=0.5x+15,
解方程组 得
x=20,
y=25.
因此气球上升20min时,
它们的高度相同,都是25m.
观察思考 探究新知
请先按暂停键!思考完成后
再按回播放键!
问题3:由于两个气球上升的速度不同,开始时2号气球高,1号气球低,那么永远如此吗?什么时刻1号气球的高度赶上2号气球的高度?你会从数和形两方面分别加以研究吗?
(2)从图形的角度研究
在同一坐标系中画出两个函数的图象,如图,
观察思考 探究新知
从中发现,当x=20时,对应的函数值相等,都是25.也就是说,两直线交于一点,交点坐标为(20,25).
请先按暂停键!思考完成后
再按回播放键!
回顾上面的解题过程,用函数观点看方程组
你得到哪些结论?你能把得到的结论推广到一般情况吗?
从“形”的角度看,解二元一次方程组相当于确定两条相应直线交点坐标.
总结:每个二元一次方程组都对应两个一次函数, 于是也对应两条直线.
从“数”的角度看,解二元一次方程组相当于求自变量为何值时,相应的两个函数值相等.
观察思考 探究新知
练习巩固 内化新知
1.若方程组 的解为 则一次函数y=2x+1与y=3x-1的图象交点坐标为________.
(2,5)
解:方程2x-y=-1可化为y=2x+1,
方程3x-y=1可化为y=3x-1,
∴方程组的解分别为对应两条直线交点的横纵坐标,
∴图象交点为(2,5)
请先按暂停键!思考完成后
再按回播放键!
练习巩固 内化新知
2.一次函数 y1= 4x + 5 与 y2 = 3x + 10 的图象如图所示,
则方程组 的解为?
O
x
y
5
y = 4x + 5
y = 3x + 10
25
解:方程4x-y=5可化为y=4x+5,
方程3x-y=-10可化为y=3x+10,
∴两条直线交点的横纵坐标,分别为对应方程组解的x,y的值,
∴方程组的解为
请先按暂停键!思考完成后
再按回播放键!
3.如图,直线 l1∶y=x+1与直线 l2∶y=mx+n 相交于点P (1,b).
(1)求b 的值.
(2)不解关于x,y 的方程组
请你直接写出它的解.
(3)直线 l3∶y=nx+m 是否也经过点P?
请说明理由.
练习巩固 内化新知
请先按暂停键!思考完成后
再按回播放键!
练习巩固 内化新知
解:(1)把P (1,b)的坐标代入 y=x+1得b=2.
(2)由(1)得P (1,2),
∴方程组 的解为
(3)直线l3∶y=nx+m 经过点P. 理由如下:
∵直线y=mx+n 经过点P (1,2),
∴m+n=2,
而把点P (1,2)代入y=nx+m也得到 m+n=2
∴直线 y=nx+m 也经过P 点.
一次函数
y=0.5x+15
二元一次方程
0.5x-y=-15
用方程观点看
用函数观点看
形
数
点的坐标满足 的函数关系
以满足函数关系的数对(x,y)为坐标画点
点的坐标满足 的方程
y=x+5
y=0.5x+15
解方程组
求自变量为何值时,相应的两个函数值相等
确定两条相应直线交点坐标
小结梳理 形成体系
以方程 的解为坐标的点都在对应一次函数图象
同学们,再见
