人教版八年级下册19.3 课题学习——选择方案 课件(25张PPT)
文档属性
| 名称 | 人教版八年级下册19.3 课题学习——选择方案 课件(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 327.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 14:23:43 | ||
图片预览

文档简介
(共25张PPT)
19.3 课题学习——选择方案
选择最佳方案
从数学的角度分析
选择方案
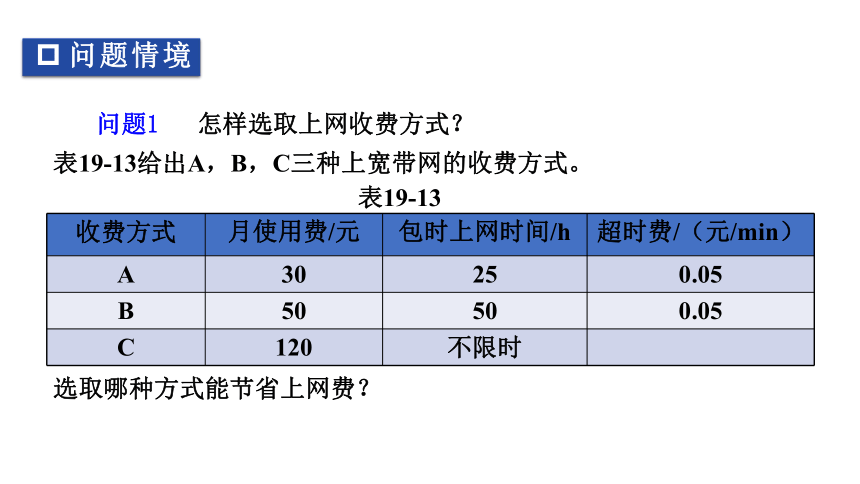
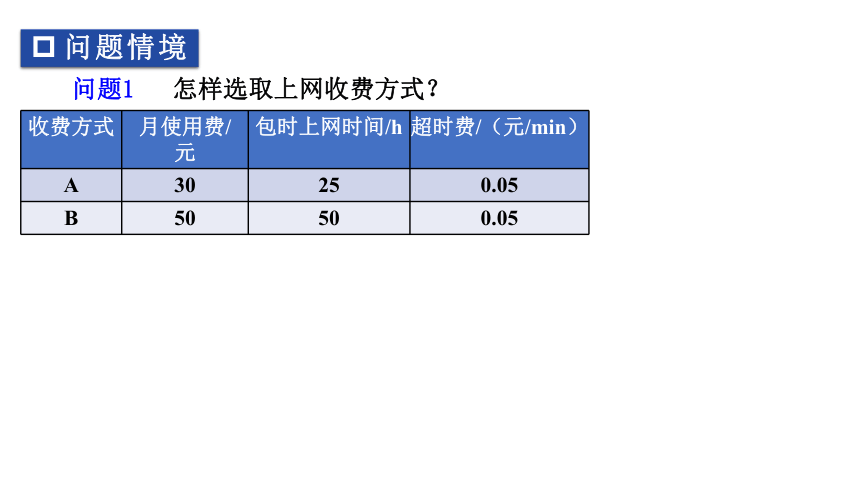
问题1 怎样选取上网收费方式?
表19-13
问题情境
表19-13给出A,B,C三种上宽带网的收费方式。
选取哪种方式能节省上网费?
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
问题情境
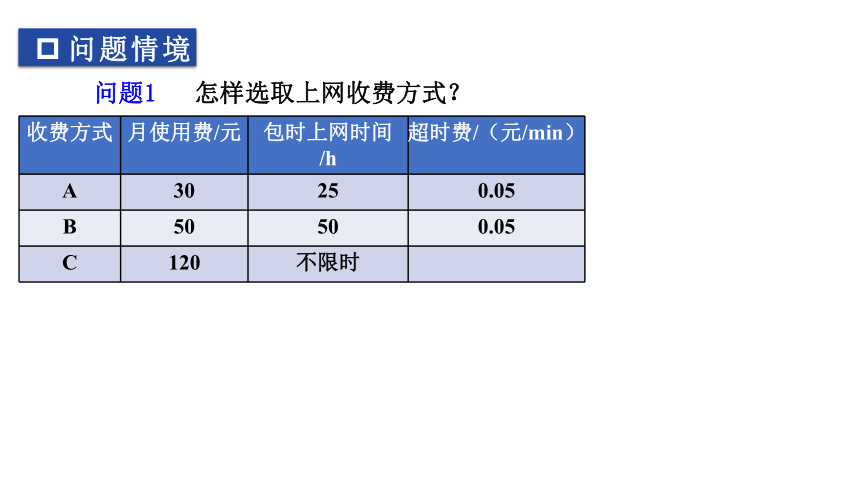
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
问题1 怎样选取上网收费方式?
问题情境
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
思考
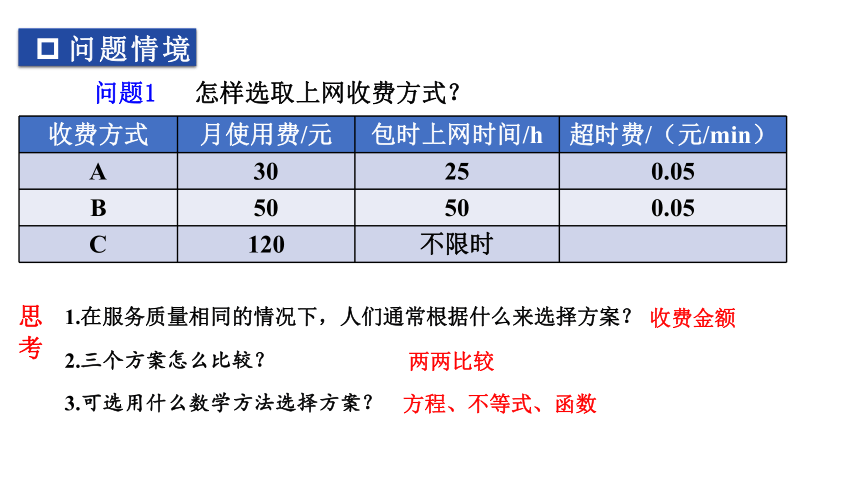
1.在服务质量相同的情况下,人们通常根据什么来选择方案?
问题1 怎样选取上网收费方式?
收费金额
2.三个方案怎么比较?
3.可选用什么数学方法选择方案?
方程、不等式、函数
两两比较
问题情境
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
问题1 怎样选取上网收费方式?
问题情境
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
思考
问题1 怎样选取上网收费方式?
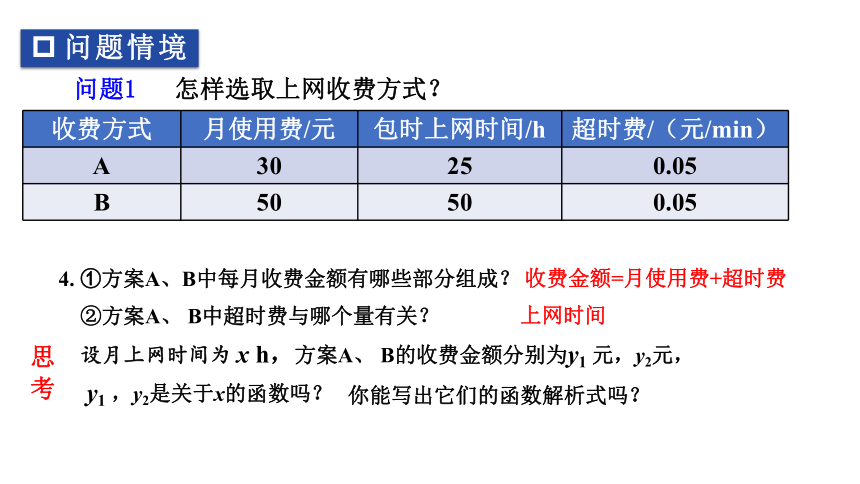
4. ①方案A、B中每月收费金额有哪些部分组成?
收费金额=月使用费+超时费
上网时间
②方案A、 B中超时费与哪个量有关?
设月上网时间为 x h,方案A、 B的收费金额分别为y1 元,y2元,
y1 ,y2是关于x的函数吗?
你能写出它们的函数解析式吗?
问题情境
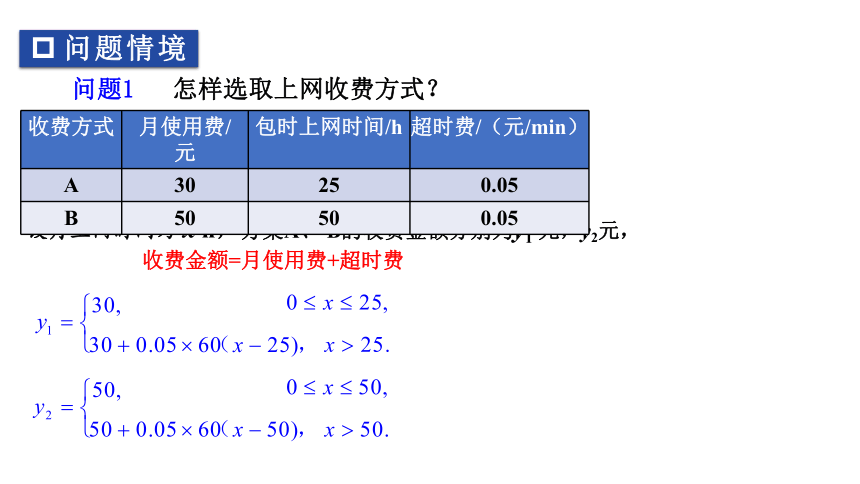
收费金额=月使用费+超时费
设月上网时间为 x h,方案A、 B的收费金额分别为y1 元,y2元,
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
问题1 怎样选取上网收费方式?
问题情境
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
问题1 怎样选取上网收费方式?
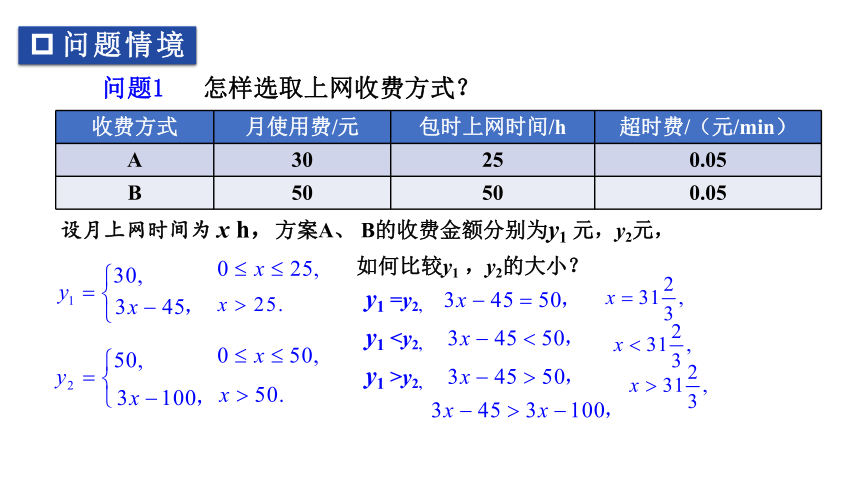
设月上网时间为 x h,方案A、 B的收费金额分别为y1 元,y2元,
如何比较y1 ,y2的大小?
y1 =y2,
y1y1 >y2,
问题情境
设月上网时间为 x h,方案A、 B的收费金额为分别y1 元,y2元,
y1 =y2,
y1y1 >y2,
综上分析,
选择A 方式最省钱;
选择B 方式最省钱;
问题情境
设月上网时间为 x h,方案A、 B的收费金额为分别y1 元,y2元,
综上分析,
选择A 方式最省钱;
选择B 方式最省钱;
怎样才能直观、快捷地选出最优方案?
问题情境
设月上网时间为 x h,方案A、 B的收费金额分别为y1 元,y2元,
函数图象
50
x
y
O
30
25
50
y1
y2
由图象可知,
选择A 方式最省钱;
选择B 方式最省钱;
问题情境
设月上网时间为 x h,方案A、 B、C的收费金额分别为y1 元,y2元, y3元。
x
y
O
30
25
50
50
y3=120,
y1
y2
120
y3
问题情境
设月上网时间为 x h,方案A、 B、C的收费金额分别为y1 元,y2元, y3元。
x
y
O
30
25
50
50
y3=120,
y1
y2
120
y3
由图象可知,
选择A 方式最省钱;
选择B 方式最省钱;
选择C 方式最省钱;
梳理归纳
实际问题
数学问题
数学模型
最佳方案
抽象
建立
解释
分析
选择
问题2 怎样租车?
现有甲乙两种大客车,它们的载客量和租金表19-14所示。
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案。
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(1)共需租多少辆汽车?
思考
1.从哪些角度考虑租多少辆汽车?
乘车人数、
租车费用。
2.若从乘车人数考虑租多少辆汽车,要满足哪些条件?
①要保证240名师生都有车坐、
②每辆汽车上至少要有1名教师
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(1)共需租多少辆汽车?
思考
从乘车人数考虑
①要保证240名师生都有车坐;
②每辆汽车上至少要有1名教师.
——汽车总数不能小于 辆;
240÷45=5……15;
6
——汽车总数不能大于 辆;
6
综合起来汽车总数为 辆;
6
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(2)给出最节省费用的租车方案.
思考
①租车费用和哪些量有关?
③这些变量之间有怎样的数量关系?
②哪些是常量;哪些是变量?
甲车数量、乙车数量.
甲车租金、乙车租金.
租车费用.
——常量
——变量
甲车数量+乙车数量=6.
租车总费用=租甲车费用+租乙车费用.
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(2)给出最节省费用的租车方案.
解:若设租用甲车为x辆,租车费用为y 元,
则y= 400 x +280(6- x )=120 x +1680,
④给出最节省费用的租车方案这个问题可以转化成怎样的数学问题?
思考
当x取何值时,y 最小.
⑤从哪些角度考虑x的取值范围?
租车总费用=租甲车费用+租乙车费用.
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(2)给出最节省费用的租车方案。
解:若设租用甲车为x辆,租车费用为y 元,
则y= 400 x +280(6- x )=120 x +1680,
从哪些角度考虑x的取值范围?
乘车人数
租车费用
——要保证240名师生都有车坐,
——总费用2300元的限额内,
45x +30(6- x )≥240,
120 x +1680 ≤2300,
解得:
x为正整数,
x取4,5,
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(2)给出最节省费用的租车方案。
解:若设租用甲车为x辆,租车费用为y 元,
则y= 400 x +280(6- x )=120 x +1680,
45x +30(6- x )≥240,
120 x +1680 ≤2300,
解得:
x为正整数,
x取4,5,
方案一:
租用甲车为4辆,乙2辆;
方案二:
租用甲车为5辆,乙1辆;
400×4+280×2=2160,
400×5+280×1=2180,
最省钱
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(2)给出最节省费用的租车方案。
解:若设租用甲车为x辆,租车费用为y 元,
则y= 400 x +280(6- x )=120 x +1680,
45x +30(6- x )≥240,
120 x +1680 ≤2300,
解得:
x为正整数,
x取4,5,
∵k=120 >0,
∴y随着x的增大而增大,
∴当x=4时, y有最小值
2160
租用甲车为4辆,乙2辆时最节省费用。
一次函数的增减性
实际问题
数学模型
问题解决
数学化
……
复盘提升
方程、不等式、函数
数学的眼光
数学的思维
数学的语言
数学建模
同学们,再见
19.3 课题学习——选择方案
选择最佳方案
从数学的角度分析
选择方案
问题1 怎样选取上网收费方式?
表19-13
问题情境
表19-13给出A,B,C三种上宽带网的收费方式。
选取哪种方式能节省上网费?
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
问题情境
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
问题1 怎样选取上网收费方式?
问题情境
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
思考
1.在服务质量相同的情况下,人们通常根据什么来选择方案?
问题1 怎样选取上网收费方式?
收费金额
2.三个方案怎么比较?
3.可选用什么数学方法选择方案?
方程、不等式、函数
两两比较
问题情境
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
问题1 怎样选取上网收费方式?
问题情境
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
思考
问题1 怎样选取上网收费方式?
4. ①方案A、B中每月收费金额有哪些部分组成?
收费金额=月使用费+超时费
上网时间
②方案A、 B中超时费与哪个量有关?
设月上网时间为 x h,方案A、 B的收费金额分别为y1 元,y2元,
y1 ,y2是关于x的函数吗?
你能写出它们的函数解析式吗?
问题情境
收费金额=月使用费+超时费
设月上网时间为 x h,方案A、 B的收费金额分别为y1 元,y2元,
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
问题1 怎样选取上网收费方式?
问题情境
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
问题1 怎样选取上网收费方式?
设月上网时间为 x h,方案A、 B的收费金额分别为y1 元,y2元,
如何比较y1 ,y2的大小?
y1 =y2,
y1
问题情境
设月上网时间为 x h,方案A、 B的收费金额为分别y1 元,y2元,
y1 =y2,
y1
综上分析,
选择A 方式最省钱;
选择B 方式最省钱;
问题情境
设月上网时间为 x h,方案A、 B的收费金额为分别y1 元,y2元,
综上分析,
选择A 方式最省钱;
选择B 方式最省钱;
怎样才能直观、快捷地选出最优方案?
问题情境
设月上网时间为 x h,方案A、 B的收费金额分别为y1 元,y2元,
函数图象
50
x
y
O
30
25
50
y1
y2
由图象可知,
选择A 方式最省钱;
选择B 方式最省钱;
问题情境
设月上网时间为 x h,方案A、 B、C的收费金额分别为y1 元,y2元, y3元。
x
y
O
30
25
50
50
y3=120,
y1
y2
120
y3
问题情境
设月上网时间为 x h,方案A、 B、C的收费金额分别为y1 元,y2元, y3元。
x
y
O
30
25
50
50
y3=120,
y1
y2
120
y3
由图象可知,
选择A 方式最省钱;
选择B 方式最省钱;
选择C 方式最省钱;
梳理归纳
实际问题
数学问题
数学模型
最佳方案
抽象
建立
解释
分析
选择
问题2 怎样租车?
现有甲乙两种大客车,它们的载客量和租金表19-14所示。
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案。
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(1)共需租多少辆汽车?
思考
1.从哪些角度考虑租多少辆汽车?
乘车人数、
租车费用。
2.若从乘车人数考虑租多少辆汽车,要满足哪些条件?
①要保证240名师生都有车坐、
②每辆汽车上至少要有1名教师
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(1)共需租多少辆汽车?
思考
从乘车人数考虑
①要保证240名师生都有车坐;
②每辆汽车上至少要有1名教师.
——汽车总数不能小于 辆;
240÷45=5……15;
6
——汽车总数不能大于 辆;
6
综合起来汽车总数为 辆;
6
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(2)给出最节省费用的租车方案.
思考
①租车费用和哪些量有关?
③这些变量之间有怎样的数量关系?
②哪些是常量;哪些是变量?
甲车数量、乙车数量.
甲车租金、乙车租金.
租车费用.
——常量
——变量
甲车数量+乙车数量=6.
租车总费用=租甲车费用+租乙车费用.
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(2)给出最节省费用的租车方案.
解:若设租用甲车为x辆,租车费用为y 元,
则y= 400 x +280(6- x )=120 x +1680,
④给出最节省费用的租车方案这个问题可以转化成怎样的数学问题?
思考
当x取何值时,y 最小.
⑤从哪些角度考虑x的取值范围?
租车总费用=租甲车费用+租乙车费用.
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(2)给出最节省费用的租车方案。
解:若设租用甲车为x辆,租车费用为y 元,
则y= 400 x +280(6- x )=120 x +1680,
从哪些角度考虑x的取值范围?
乘车人数
租车费用
——要保证240名师生都有车坐,
——总费用2300元的限额内,
45x +30(6- x )≥240,
120 x +1680 ≤2300,
解得:
x为正整数,
x取4,5,
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(2)给出最节省费用的租车方案。
解:若设租用甲车为x辆,租车费用为y 元,
则y= 400 x +280(6- x )=120 x +1680,
45x +30(6- x )≥240,
120 x +1680 ≤2300,
解得:
x为正整数,
x取4,5,
方案一:
租用甲车为4辆,乙2辆;
方案二:
租用甲车为5辆,乙1辆;
400×4+280×2=2160,
400×5+280×1=2180,
最省钱
问题情境
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金/(元/辆) 400 280
(2)给出最节省费用的租车方案。
解:若设租用甲车为x辆,租车费用为y 元,
则y= 400 x +280(6- x )=120 x +1680,
45x +30(6- x )≥240,
120 x +1680 ≤2300,
解得:
x为正整数,
x取4,5,
∵k=120 >0,
∴y随着x的增大而增大,
∴当x=4时, y有最小值
2160
租用甲车为4辆,乙2辆时最节省费用。
一次函数的增减性
实际问题
数学模型
问题解决
数学化
……
复盘提升
方程、不等式、函数
数学的眼光
数学的思维
数学的语言
数学建模
同学们,再见
