初中数学人教版八年级下册第二十章 数据的分析 小结课件(17张PPT)
文档属性
| 名称 | 初中数学人教版八年级下册第二十章 数据的分析 小结课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 254.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
数据分析小结
年 级:八年级
学 科:初中数学(人教版)
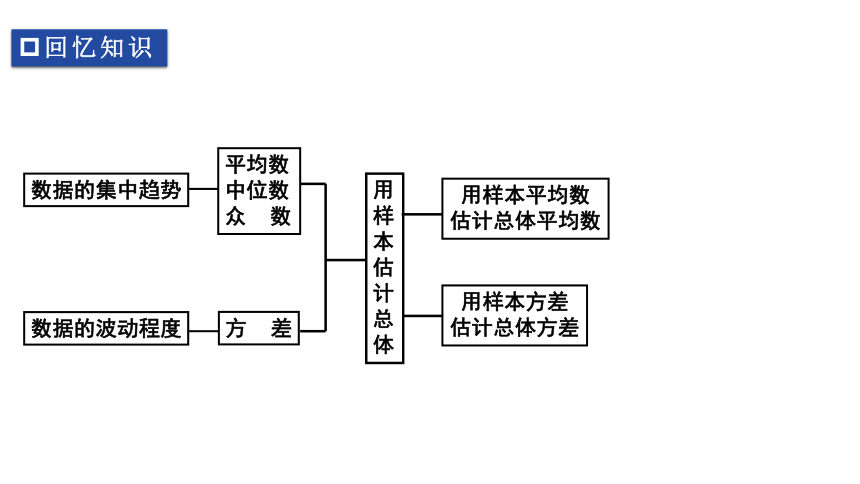
回忆知识
数据的集中趋势
平均数
中位数
众 数
数据的波动程度
方 差
用
样
本
估
计
总
体
用样本平均数
估计总体平均数
用样本方差
估计总体方差
一、数据的集中趋势
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平 均数 一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这 n 个数的平均数.
加权平 均数 一般地,若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,则
叫做这 n 个数的加权平均数.
回忆知识
回忆知识
中位数 定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间___________________就是这组数据的中位数.
防错 提醒 确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定.
众 数 定义 一组数据中出现次数________的数据叫做这组数据的众数.
防错 提醒 (1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析.
中间位置的数
两个数据的平均数
最多
回忆知识
表示波 动的量 定义 意义
方差 设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________ 来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作 s2 方差越大,数据的波动越___,反之也成立
平均数
大
二、数据的波动程度
基础巩固
1.某4S店今年1~5月新能源汽车的销量(辆数)分别如下:25,33,36,31,40,这组数据的平均数是( )
A.34 B.33 C.32.5 D.31
这组数据的平均数为(25+33+36+31+40)÷5=33.
B
2.某路段的一台机动车雷达测速仪记录了一段时间内通过的机动车的车速数据如下:67,63,69,55,65,则该组数据的中位数为( B )
A.63 B.65 C.66 D.69
将这组数据按由小到大的顺序排列,为55,63,65,67,69,所以这组数据的中位数是65.
B
基础巩固
4.一组数据中的一个数大小发生了变化,一定会影响这组数据的平均数、众数、中位数中的 ( )
A.1个 B.2个 C.3个 D.0个
3.某米店经营某种品牌的大米,该店记录了一周中不同包装(10 kg,20 kg,50 kg)的大米的销售量(单位:袋)如下:10 kg装100袋;20 kg装220袋;50 kg装80袋.如果每500 g大米的进价和售价都相同,则他最应该关注的是这些销售数据(袋数)中的( )
A.平均数 B.中位数 C.众数 D.最大值
C
A
基础巩固
5.今年我国小麦大丰收,农业专家在某种植片区随机抽取了10株小麦,测得其麦穗长(单位:cm)分别为8,8,6,7,9,9,7,8,10,8,那么这一组数据的方差为( D )
A.1.5 B.1.4 C.1.3 D.1.2
D
基础巩固
6.人数相同的八年级(1)、(2)两班学生在同一次数学单元测试中,班级平均分和方差如下: , , ,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
7.五个数1,3,a,5,8的平均数是4,则a =_____,这五个数的方差是_____.
3
5.6
提升优化
8.为迎接亚运会在某市的召开,该市将举办以“我为运动添光彩”为主题的演讲比赛.某县经过紧张的预赛,王锐、李红和张敏三人脱颖而出,他们的创作部分和演讲部分的成绩如下表所示,扇形统计图是当地的450名演讲爱好者对他们三人进行“我喜欢的选手”投票后的统计情况(没有弃权票,并且每人只能推选1人).
王锐 李红 张敏
创作 95分 90分 88分
演讲 82分 85分 90分
提升优化
王锐 李红 张敏
创作 95分 90分 88分
演讲 82分 85分 90分
(1)请计算三位参赛选手的得票数各是多少?
解:(1)由题意,王锐的得票数:30%×450=135(张);
李红的得票数:36%×450=162(张);
张敏的得票数:34%×450=153(张).
提升优化
王锐 李红 张敏
创作 95分 90分 88分
演讲 82分 85分 90分
(2)现要从王锐、李红和张敏三人中推选一人代表该地区参加全市的决赛,推选方案为:①演讲爱好者所投票,每票记1分;②将创作、演讲、得票三项所得分按4∶5∶1的比例确定个人成绩.请计算三位选手的个人成绩,从他们的个人成绩看,谁将会被推选参加该市的决赛?
(2)王锐的个人成绩:
王锐的得票数135张
李红的得票数162张
张敏的得票数153张
李红的个人成绩:
张敏的个人成绩:
∴张敏将会被推选参加该市的决赛.
提升优化
9.某市在开展节约用水活动中,对某小区 200 户居民家庭用水情况进行统计分析,其中3月份比2月份节约用水情况如下表所示:
节水量(m3) 1 1.5 2
户数 20 120 60
(1) 抽取的 200 户家庭节水量的平均数是_____,中位数是______,众数是_______.
提升优化
(2) 根据以上数据,估计某市 100 万户居民家庭 3 月份
比 2 月份的节约用水量是_________.
解:
平均数:
中位数:200÷2 = 100,则求第 100 个人和 101 个人的节水量的平均数. 由表可知其都为1.5,所以中位数 1.5.
众数:户数最多的节水量:1.5 .
160 万m3
节水量(m3) 1 1.5 2
户数 20 120 60
估计总体平均数
样本平均数
10.为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的零件个数、直径等相关数据依次如下图所示(单位:mm).根据测试得到的有关数据,试解答下列问题:
提升优化
(1)考虑平均数与完全符合要求的个数,你认为 的成绩好些;
(2)计算出s2B的大小,考虑平均数与方差,说明谁的成绩好些;
B
∴B的成绩更稳定
提升优化
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个后实际情况,你认为派谁去参赛较合适?说明你的理由.
解:由(2)可知B的成绩较为稳定,且由图象可看出,B加工的第九个零件后成绩越来越好,而竞赛中加工零件个数远远超过10个,所以应派B去参赛.
提升优化
0.008
同学们,再见
数据分析小结
年 级:八年级
学 科:初中数学(人教版)
回忆知识
数据的集中趋势
平均数
中位数
众 数
数据的波动程度
方 差
用
样
本
估
计
总
体
用样本平均数
估计总体平均数
用样本方差
估计总体方差
一、数据的集中趋势
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平 均数 一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这 n 个数的平均数.
加权平 均数 一般地,若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,则
叫做这 n 个数的加权平均数.
回忆知识
回忆知识
中位数 定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间___________________就是这组数据的中位数.
防错 提醒 确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定.
众 数 定义 一组数据中出现次数________的数据叫做这组数据的众数.
防错 提醒 (1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析.
中间位置的数
两个数据的平均数
最多
回忆知识
表示波 动的量 定义 意义
方差 设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________ 来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作 s2 方差越大,数据的波动越___,反之也成立
平均数
大
二、数据的波动程度
基础巩固
1.某4S店今年1~5月新能源汽车的销量(辆数)分别如下:25,33,36,31,40,这组数据的平均数是( )
A.34 B.33 C.32.5 D.31
这组数据的平均数为(25+33+36+31+40)÷5=33.
B
2.某路段的一台机动车雷达测速仪记录了一段时间内通过的机动车的车速数据如下:67,63,69,55,65,则该组数据的中位数为( B )
A.63 B.65 C.66 D.69
将这组数据按由小到大的顺序排列,为55,63,65,67,69,所以这组数据的中位数是65.
B
基础巩固
4.一组数据中的一个数大小发生了变化,一定会影响这组数据的平均数、众数、中位数中的 ( )
A.1个 B.2个 C.3个 D.0个
3.某米店经营某种品牌的大米,该店记录了一周中不同包装(10 kg,20 kg,50 kg)的大米的销售量(单位:袋)如下:10 kg装100袋;20 kg装220袋;50 kg装80袋.如果每500 g大米的进价和售价都相同,则他最应该关注的是这些销售数据(袋数)中的( )
A.平均数 B.中位数 C.众数 D.最大值
C
A
基础巩固
5.今年我国小麦大丰收,农业专家在某种植片区随机抽取了10株小麦,测得其麦穗长(单位:cm)分别为8,8,6,7,9,9,7,8,10,8,那么这一组数据的方差为( D )
A.1.5 B.1.4 C.1.3 D.1.2
D
基础巩固
6.人数相同的八年级(1)、(2)两班学生在同一次数学单元测试中,班级平均分和方差如下: , , ,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
7.五个数1,3,a,5,8的平均数是4,则a =_____,这五个数的方差是_____.
3
5.6
提升优化
8.为迎接亚运会在某市的召开,该市将举办以“我为运动添光彩”为主题的演讲比赛.某县经过紧张的预赛,王锐、李红和张敏三人脱颖而出,他们的创作部分和演讲部分的成绩如下表所示,扇形统计图是当地的450名演讲爱好者对他们三人进行“我喜欢的选手”投票后的统计情况(没有弃权票,并且每人只能推选1人).
王锐 李红 张敏
创作 95分 90分 88分
演讲 82分 85分 90分
提升优化
王锐 李红 张敏
创作 95分 90分 88分
演讲 82分 85分 90分
(1)请计算三位参赛选手的得票数各是多少?
解:(1)由题意,王锐的得票数:30%×450=135(张);
李红的得票数:36%×450=162(张);
张敏的得票数:34%×450=153(张).
提升优化
王锐 李红 张敏
创作 95分 90分 88分
演讲 82分 85分 90分
(2)现要从王锐、李红和张敏三人中推选一人代表该地区参加全市的决赛,推选方案为:①演讲爱好者所投票,每票记1分;②将创作、演讲、得票三项所得分按4∶5∶1的比例确定个人成绩.请计算三位选手的个人成绩,从他们的个人成绩看,谁将会被推选参加该市的决赛?
(2)王锐的个人成绩:
王锐的得票数135张
李红的得票数162张
张敏的得票数153张
李红的个人成绩:
张敏的个人成绩:
∴张敏将会被推选参加该市的决赛.
提升优化
9.某市在开展节约用水活动中,对某小区 200 户居民家庭用水情况进行统计分析,其中3月份比2月份节约用水情况如下表所示:
节水量(m3) 1 1.5 2
户数 20 120 60
(1) 抽取的 200 户家庭节水量的平均数是_____,中位数是______,众数是_______.
提升优化
(2) 根据以上数据,估计某市 100 万户居民家庭 3 月份
比 2 月份的节约用水量是_________.
解:
平均数:
中位数:200÷2 = 100,则求第 100 个人和 101 个人的节水量的平均数. 由表可知其都为1.5,所以中位数 1.5.
众数:户数最多的节水量:1.5 .
160 万m3
节水量(m3) 1 1.5 2
户数 20 120 60
估计总体平均数
样本平均数
10.为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的零件个数、直径等相关数据依次如下图所示(单位:mm).根据测试得到的有关数据,试解答下列问题:
提升优化
(1)考虑平均数与完全符合要求的个数,你认为 的成绩好些;
(2)计算出s2B的大小,考虑平均数与方差,说明谁的成绩好些;
B
∴B的成绩更稳定
提升优化
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个后实际情况,你认为派谁去参赛较合适?说明你的理由.
解:由(2)可知B的成绩较为稳定,且由图象可看出,B加工的第九个零件后成绩越来越好,而竞赛中加工零件个数远远超过10个,所以应派B去参赛.
提升优化
0.008
同学们,再见
