将军饮马模型(知识梳理与考点分类讲解)(含解析)
文档属性
| 名称 | 将军饮马模型(知识梳理与考点分类讲解)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1014.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-25 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
将军饮马模型(知识梳理与考点分类讲解)
【模型一 两点交点型】如图1,直线l和l的异侧两点A.B,在直线l上求作一点P,使PA+PB最小。
图1
【模型二 两点一动型】如图2,直线l和l的同侧两点A.B,在直线l上求作一点P,使PA+PB最小
图2
【模型三 一定两动型】如图3,点P是∠MON内的一点,分别在OM,ON上作点A,B。使△PAB的周长最小
图3
【模型四 两点两动型】如图4,点P,Q为∠MON内的两点,分别在OM,ON上作点A,B。使四边形PAQB的 周长最小。
图4
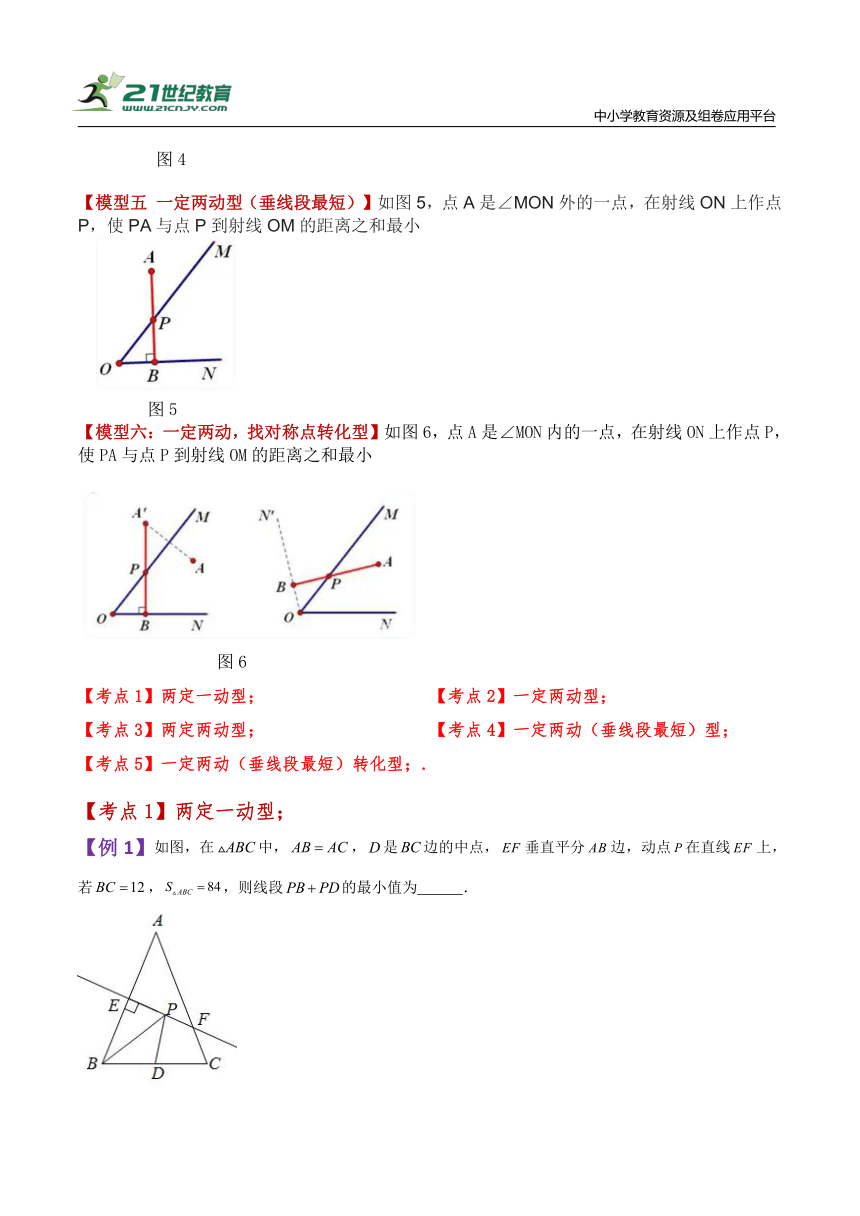
【模型五 一定两动型(垂线段最短)】如图5,点A是∠MON外的一点,在射线ON上作点P,使PA与点P到射线OM的距离之和最小
图5
【模型六:一定两动,找对称点转化型】如图6,点A是∠MON内的一点,在射线ON上作点P,使PA与点P到射线OM的距离之和最小
图6
【考点1】两定一动型; 【考点2】一定两动型;
【考点3】两定两动型; 【考点4】一定两动(垂线段最短)型;
【考点5】一定两动(垂线段最短)转化型;.
【考点1】两定一动型;
【例1】如图,在中,,是边的中点,垂直平分边,动点在直线上,若,,则线段的最小值为 .
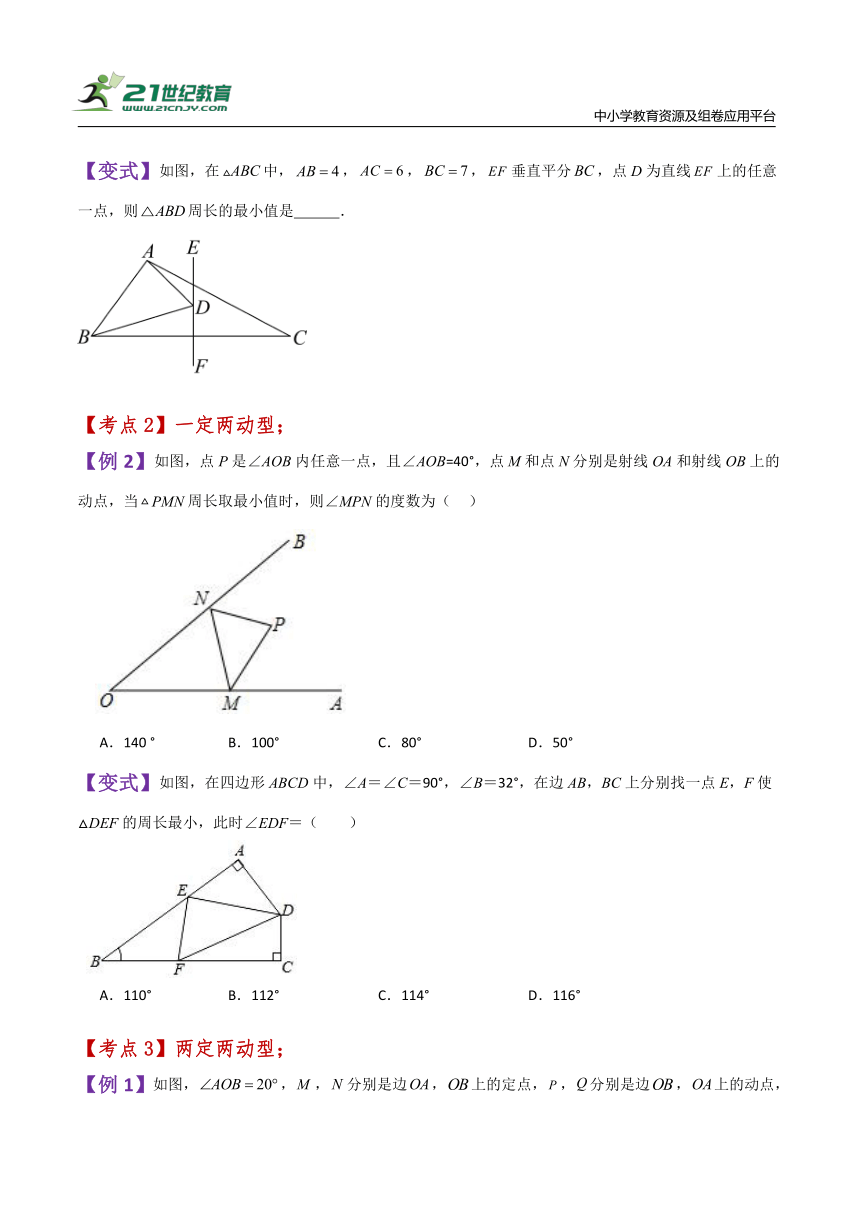
【变式】如图,在中,,,,垂直平分,点D为直线上的任意一点,则周长的最小值是 .
【考点2】一定两动型;
【例2】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当PMN周长取最小值时,则∠MPN的度数为( )
A.140 ° B.100° C.80° D.50°
【变式】如图,在四边形ABCD中,∠A=∠C=90°,∠B=32°,在边AB,BC上分别找一点E,F使△DEF的周长最小,此时∠EDF=( )
A.110° B.112° C.114° D.116°
【考点3】两定两动型;
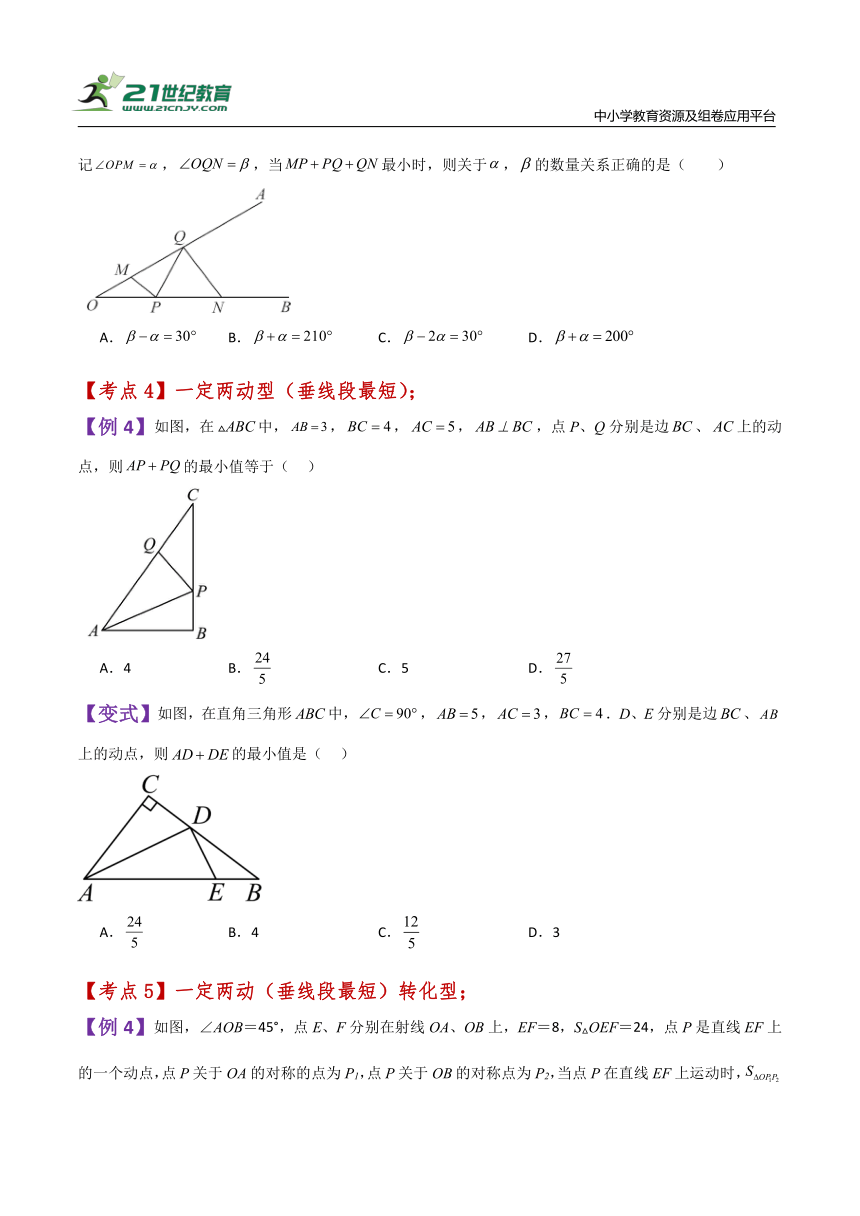
【例1】如图,,,分别是边,上的定点,,分别是边,上的动点,记,,当最小时,则关于,的数量关系正确的是( )
A. B. C. D.
【考点4】一定两动型(垂线段最短);
【例4】如图,在中,,,,,点P、Q分别是边、上的动点,则的最小值等于( )
A.4 B. C.5 D.
【变式】如图,在直角三角形中,,,,.D、E分别是边、上的动点,则的最小值是( )
A. B.4 C. D.3
【考点5】一定两动(垂线段最短)转化型;
【例4】如图,∠AOB=45°,点E、F分别在射线OA、OB上,EF=8,S△OEF=24,点P是直线EF上的一个动点,点P关于OA的对称的点为P1,点P关于OB的对称点为P2,当点P在直线EF上运动时,的最小值为( )
A.8 B.16 C.18 D.36
【变式】如图,在中,,,,,是的平分线.若点P,Q分别是和上的动点,则的最小值是
解析
【考点1】两定一动型;
【例1】如图,在中,,是边的中点,垂直平分边,动点在直线上,若,,则线段的最小值为 .
【答案】14
【分析】根据三角形的面积公式得到AD=14,由EF垂直平分AB,得到点A,B关于直线EF对称,于是得到AD的长度=PB+PD的最小值,即可得到结论.
解:∵AB=AC,D是BC中点,
∴AD⊥BC,
又∵BC=12,S△ABC=84,
∴×12×AD=84,
∴AD=14,
∵EF垂直平分AB,
∴PA=PB,
∴PB+PD=PA+PD,
∴当A,P,D在同一直线上时,PB+PD=PA+PD=AD,
即AD的长度=PB+PD的最小值,
∴PB+PD的最小值为14,
故答案为:14.
【点拨】本题考查了轴对称-最短路线问题,线段的垂直平分线的性质,等腰三角形的性质,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
【变式】如图,在中,,,,垂直平分,点D为直线上的任意一点,则周长的最小值是 .
【答案】10
【分析】本题考查了轴对称最短路线问题的应用,垂直平分线的性质,准确找出点D的位置是解答本题的关键.根据垂直平分线的性质可知,点B与点C关于对称,故当点D与点P重合时,的值最小,最小值等于的长,由此即可得到答案.
解:垂直平分,
点B与点C关于对称,
如图,设与相较于点P,
当点D与点P重合时,的值最小,最小值等于的长,
,,
周长的最小值是,
故答案为:10.
【考点2】一定两动型;
【例2】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当PMN周长取最小值时,则∠MPN的度数为( )
A.140 ° B.100° C.80° D.50°
【答案】B
【分析】分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,△PMN的周长=P1P2,然后得到等腰△OP1P2中,∠OP1P2+∠OP2P1=100°,即可得出∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=100°.
解:分别作点P关于OA、OB的对称点P1、P2,连接P1P2,交OA于M,交OB于N,
则OP1=OP=OP2,∠OP1M=∠MPO,∠NPO=∠NP2O,
根据轴对称的性质,可得MP=P1M,PN=P2N,则
△PMN的周长的最小值=P1P2,
∴∠P1OP2=2∠AOB=80°,
∴等腰△OP1P2中,∠OP1P2+∠OP2P1=100°,
∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=100°,
故选:B.
【点拨】本题考查了轴对称 最短路线问题,正确作出辅助线,得到等腰△OP1P2中∠OP1P2+∠OP2P1=100°是关键.凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.
【变式】如图,在四边形ABCD中,∠A=∠C=90°,∠B=32°,在边AB,BC上分别找一点E,F使△DEF的周长最小,此时∠EDF=( )
A.110° B.112° C.114° D.116°
【答案】D
【分析】如图,作点D关于BA的对称点P,点D关于BC的对称点Q,连接PQ,交AB于E′,交BC于F′,则点E′,F′即为所求,结合四边形的内角和即可得出答案.
解:如图,作点D关于BA的对称点P,点D关于BC的对称点Q,连接PQ,交AB于E′,交BC于F′,则点E′,F′即为所求.
∵四边形ABCD中,∠A=∠C=90°,∠B=32°,
∴∠ADC=180°﹣32°,
由轴对称知,∠ADE′=∠P,∠CDF′=∠Q,
在△PDQ中,
∠P+∠Q=180°﹣∠ADC
=180°﹣(180°﹣32°)
=32°,
∴∠ADE′+∠CDF′=∠P+∠Q=32°,
∴∠E′DF′=∠ADC﹣(∠ADE′+∠CDF′)
=180°﹣32°-32°
=116°.
故选:D.
【点拨】本题考查的是轴对称-最短路线问题,涉及到平面内最短线路问题求法以及四边形的内角和定理等知识,根据已知得出E,F的位置是解题的关键.
【考点3】两定两动型;
【例1】如图,,,分别是边,上的定点,,分别是边,上的动点,记,,当最小时,则关于,的数量关系正确的是( )
A. B. C. D.
【答案】D
【分析】如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则最小,易知,,,,,由此即可解决问题.
解:如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则最小,
由轴对称的性质得,,,,,
∴.
故选:D.
【点拨】本题考查轴对称-最短问题、三角形的内角和定理.三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
【考点4】一定两动型(垂线段最短);
【例4】如图,在中,,,,,点P、Q分别是边、上的动点,则的最小值等于( )
A.4 B. C.5 D.
【答案】B
【分析】作过于的对称点,过点作,交于点,交于点,根据对称可得:,得到当三点共线时,最小,再根据垂线段最短,得到时,最小,进行求解即可.
解:作过于的对称点,过点作,交于点,交于点,
∵,
∴当三点共线时,最小,
∵垂线段最短,
∴时,最小,
连接,
∵关于对称,
∴,
∴,
∵,
∴,即:,
∴;
故选B.
【点拨】本题考查利用轴对称求线段和最小问题.熟练掌握通过构造轴对称,解决线段和最小,以及点到直线,垂线段最短,是解题的关键.
【变式】如图,在直角三角形中,,,,.D、E分别是边、上的动点,则的最小值是( )
A. B.4 C. D.3
【答案】A
【分析】本题考查了轴对称的性质,垂线段最短,等积法求高,作点关于的对称点,过点作于点,交于点,连接,得到此时有最小值,再根据求出的长,即可得到答案.
解:如图,作点关于的对称点,过点作于点,交于点,连接,
由对称的性质可知,,,,
,此时有最小值,
,,,
,
,
,即的最小值为,
故选:A
【考点5】一定两动(垂线段最短)转化型;
【例4】如图,∠AOB=45°,点E、F分别在射线OA、OB上,EF=8,S△OEF=24,点P是直线EF上的一个动点,点P关于OA的对称的点为P1,点P关于OB的对称点为P2,当点P在直线EF上运动时,的最小值为( )
A.8 B.16 C.18 D.36
【答案】C
【分析】连接OP,过点O作交EF的延长线于点H,先用三角形面积公式求出OH,再证明是等腰直角三角形,当OP最小时,的面积最小.
解:如图所示,连接OP,过点O作交EF的延长线于点H,
∵EF=8,,
∴OH=6,
∵点P关于OA对称的点,点P关于OB对称点为,
∴,,,
∵,
∴,
∴是等腰直角三角形,
∴最小时,的面积最小,
根据垂线段最短可知,OP的最小值为6,
∴的面积最小值为:,
故选C.
【点拨】本题考查了轴对称的性质,解题的关键是构造出三角形OEF的高,掌握轴对称的性质和垂线段最短.
【变式】如图,在中,,,,,是的平分线.若点P,Q分别是和上的动点,则的最小值是
【答案】
【分析】在上截取,连接,,可证,根据全等三角形的性质可知点和点关于对称,再根据轴对称的性质及最短路径结合面积法即可得出答案.
解:如图,在上截取,连接,,
是的平分线,
在与中
点和点关于对称,连接,与交于点,连接,
此时,
是动点,
也是动点,当与垂直时,最小,即最小.
此时,由面积法得.
故答案为:.
【点拨】本题考查利用轴对称求最短距离,能够利用轴对称将线段和的最小值转化为线段长求解是关键.
将军饮马模型(知识梳理与考点分类讲解)
【模型一 两点交点型】如图1,直线l和l的异侧两点A.B,在直线l上求作一点P,使PA+PB最小。
图1
【模型二 两点一动型】如图2,直线l和l的同侧两点A.B,在直线l上求作一点P,使PA+PB最小
图2
【模型三 一定两动型】如图3,点P是∠MON内的一点,分别在OM,ON上作点A,B。使△PAB的周长最小
图3
【模型四 两点两动型】如图4,点P,Q为∠MON内的两点,分别在OM,ON上作点A,B。使四边形PAQB的 周长最小。
图4
【模型五 一定两动型(垂线段最短)】如图5,点A是∠MON外的一点,在射线ON上作点P,使PA与点P到射线OM的距离之和最小
图5
【模型六:一定两动,找对称点转化型】如图6,点A是∠MON内的一点,在射线ON上作点P,使PA与点P到射线OM的距离之和最小
图6
【考点1】两定一动型; 【考点2】一定两动型;
【考点3】两定两动型; 【考点4】一定两动(垂线段最短)型;
【考点5】一定两动(垂线段最短)转化型;.
【考点1】两定一动型;
【例1】如图,在中,,是边的中点,垂直平分边,动点在直线上,若,,则线段的最小值为 .
【变式】如图,在中,,,,垂直平分,点D为直线上的任意一点,则周长的最小值是 .
【考点2】一定两动型;
【例2】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当PMN周长取最小值时,则∠MPN的度数为( )
A.140 ° B.100° C.80° D.50°
【变式】如图,在四边形ABCD中,∠A=∠C=90°,∠B=32°,在边AB,BC上分别找一点E,F使△DEF的周长最小,此时∠EDF=( )
A.110° B.112° C.114° D.116°
【考点3】两定两动型;
【例1】如图,,,分别是边,上的定点,,分别是边,上的动点,记,,当最小时,则关于,的数量关系正确的是( )
A. B. C. D.
【考点4】一定两动型(垂线段最短);
【例4】如图,在中,,,,,点P、Q分别是边、上的动点,则的最小值等于( )
A.4 B. C.5 D.
【变式】如图,在直角三角形中,,,,.D、E分别是边、上的动点,则的最小值是( )
A. B.4 C. D.3
【考点5】一定两动(垂线段最短)转化型;
【例4】如图,∠AOB=45°,点E、F分别在射线OA、OB上,EF=8,S△OEF=24,点P是直线EF上的一个动点,点P关于OA的对称的点为P1,点P关于OB的对称点为P2,当点P在直线EF上运动时,的最小值为( )
A.8 B.16 C.18 D.36
【变式】如图,在中,,,,,是的平分线.若点P,Q分别是和上的动点,则的最小值是
解析
【考点1】两定一动型;
【例1】如图,在中,,是边的中点,垂直平分边,动点在直线上,若,,则线段的最小值为 .
【答案】14
【分析】根据三角形的面积公式得到AD=14,由EF垂直平分AB,得到点A,B关于直线EF对称,于是得到AD的长度=PB+PD的最小值,即可得到结论.
解:∵AB=AC,D是BC中点,
∴AD⊥BC,
又∵BC=12,S△ABC=84,
∴×12×AD=84,
∴AD=14,
∵EF垂直平分AB,
∴PA=PB,
∴PB+PD=PA+PD,
∴当A,P,D在同一直线上时,PB+PD=PA+PD=AD,
即AD的长度=PB+PD的最小值,
∴PB+PD的最小值为14,
故答案为:14.
【点拨】本题考查了轴对称-最短路线问题,线段的垂直平分线的性质,等腰三角形的性质,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
【变式】如图,在中,,,,垂直平分,点D为直线上的任意一点,则周长的最小值是 .
【答案】10
【分析】本题考查了轴对称最短路线问题的应用,垂直平分线的性质,准确找出点D的位置是解答本题的关键.根据垂直平分线的性质可知,点B与点C关于对称,故当点D与点P重合时,的值最小,最小值等于的长,由此即可得到答案.
解:垂直平分,
点B与点C关于对称,
如图,设与相较于点P,
当点D与点P重合时,的值最小,最小值等于的长,
,,
周长的最小值是,
故答案为:10.
【考点2】一定两动型;
【例2】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当PMN周长取最小值时,则∠MPN的度数为( )
A.140 ° B.100° C.80° D.50°
【答案】B
【分析】分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,△PMN的周长=P1P2,然后得到等腰△OP1P2中,∠OP1P2+∠OP2P1=100°,即可得出∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=100°.
解:分别作点P关于OA、OB的对称点P1、P2,连接P1P2,交OA于M,交OB于N,
则OP1=OP=OP2,∠OP1M=∠MPO,∠NPO=∠NP2O,
根据轴对称的性质,可得MP=P1M,PN=P2N,则
△PMN的周长的最小值=P1P2,
∴∠P1OP2=2∠AOB=80°,
∴等腰△OP1P2中,∠OP1P2+∠OP2P1=100°,
∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=100°,
故选:B.
【点拨】本题考查了轴对称 最短路线问题,正确作出辅助线,得到等腰△OP1P2中∠OP1P2+∠OP2P1=100°是关键.凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.
【变式】如图,在四边形ABCD中,∠A=∠C=90°,∠B=32°,在边AB,BC上分别找一点E,F使△DEF的周长最小,此时∠EDF=( )
A.110° B.112° C.114° D.116°
【答案】D
【分析】如图,作点D关于BA的对称点P,点D关于BC的对称点Q,连接PQ,交AB于E′,交BC于F′,则点E′,F′即为所求,结合四边形的内角和即可得出答案.
解:如图,作点D关于BA的对称点P,点D关于BC的对称点Q,连接PQ,交AB于E′,交BC于F′,则点E′,F′即为所求.
∵四边形ABCD中,∠A=∠C=90°,∠B=32°,
∴∠ADC=180°﹣32°,
由轴对称知,∠ADE′=∠P,∠CDF′=∠Q,
在△PDQ中,
∠P+∠Q=180°﹣∠ADC
=180°﹣(180°﹣32°)
=32°,
∴∠ADE′+∠CDF′=∠P+∠Q=32°,
∴∠E′DF′=∠ADC﹣(∠ADE′+∠CDF′)
=180°﹣32°-32°
=116°.
故选:D.
【点拨】本题考查的是轴对称-最短路线问题,涉及到平面内最短线路问题求法以及四边形的内角和定理等知识,根据已知得出E,F的位置是解题的关键.
【考点3】两定两动型;
【例1】如图,,,分别是边,上的定点,,分别是边,上的动点,记,,当最小时,则关于,的数量关系正确的是( )
A. B. C. D.
【答案】D
【分析】如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则最小,易知,,,,,由此即可解决问题.
解:如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则最小,
由轴对称的性质得,,,,,
∴.
故选:D.
【点拨】本题考查轴对称-最短问题、三角形的内角和定理.三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
【考点4】一定两动型(垂线段最短);
【例4】如图,在中,,,,,点P、Q分别是边、上的动点,则的最小值等于( )
A.4 B. C.5 D.
【答案】B
【分析】作过于的对称点,过点作,交于点,交于点,根据对称可得:,得到当三点共线时,最小,再根据垂线段最短,得到时,最小,进行求解即可.
解:作过于的对称点,过点作,交于点,交于点,
∵,
∴当三点共线时,最小,
∵垂线段最短,
∴时,最小,
连接,
∵关于对称,
∴,
∴,
∵,
∴,即:,
∴;
故选B.
【点拨】本题考查利用轴对称求线段和最小问题.熟练掌握通过构造轴对称,解决线段和最小,以及点到直线,垂线段最短,是解题的关键.
【变式】如图,在直角三角形中,,,,.D、E分别是边、上的动点,则的最小值是( )
A. B.4 C. D.3
【答案】A
【分析】本题考查了轴对称的性质,垂线段最短,等积法求高,作点关于的对称点,过点作于点,交于点,连接,得到此时有最小值,再根据求出的长,即可得到答案.
解:如图,作点关于的对称点,过点作于点,交于点,连接,
由对称的性质可知,,,,
,此时有最小值,
,,,
,
,
,即的最小值为,
故选:A
【考点5】一定两动(垂线段最短)转化型;
【例4】如图,∠AOB=45°,点E、F分别在射线OA、OB上,EF=8,S△OEF=24,点P是直线EF上的一个动点,点P关于OA的对称的点为P1,点P关于OB的对称点为P2,当点P在直线EF上运动时,的最小值为( )
A.8 B.16 C.18 D.36
【答案】C
【分析】连接OP,过点O作交EF的延长线于点H,先用三角形面积公式求出OH,再证明是等腰直角三角形,当OP最小时,的面积最小.
解:如图所示,连接OP,过点O作交EF的延长线于点H,
∵EF=8,,
∴OH=6,
∵点P关于OA对称的点,点P关于OB对称点为,
∴,,,
∵,
∴,
∴是等腰直角三角形,
∴最小时,的面积最小,
根据垂线段最短可知,OP的最小值为6,
∴的面积最小值为:,
故选C.
【点拨】本题考查了轴对称的性质,解题的关键是构造出三角形OEF的高,掌握轴对称的性质和垂线段最短.
【变式】如图,在中,,,,,是的平分线.若点P,Q分别是和上的动点,则的最小值是
【答案】
【分析】在上截取,连接,,可证,根据全等三角形的性质可知点和点关于对称,再根据轴对称的性质及最短路径结合面积法即可得出答案.
解:如图,在上截取,连接,,
是的平分线,
在与中
点和点关于对称,连接,与交于点,连接,
此时,
是动点,
也是动点,当与垂直时,最小,即最小.
此时,由面积法得.
故答案为:.
【点拨】本题考查利用轴对称求最短距离,能够利用轴对称将线段和的最小值转化为线段长求解是关键.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
