初中数学沪科版九年级上册 第22章 相似形 综合素质评价(含答案)
文档属性
| 名称 | 初中数学沪科版九年级上册 第22章 相似形 综合素质评价(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 751.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 15:00:52 | ||
图片预览




文档简介
第22章 相似形 综合素质评价
一、选择题(本大题共10小题,每小题4分,满分40分)
1.有下列说法:①所有的等腰三角形都相似;②所有的等边三角形都相似;③所有的正方形都相似;④所有的矩形都相似,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.[母题:教材P69练习T3 ]若2x=5y(x,y≠0),则下列式子中错误的是( )
A.= B.= C.= D.=
3. 在设计人体雕像时,为了增加视觉美感,会使雕像上部(腰部以上)与下部(腰部以下)的高度比等于下部与全部的高度比等于(≈0.618,称为黄金分割比例),按此比例设计一座高度为2 m的雷锋雕像,那么该雕像的下部设计高度是( )
A.(-1)m B.(3-)m C.(-1)m D.(3-)m
4.[母题:教材P71练习T3 ]如图,AB∥CD∥EF,BE与AF相交于点H,且AH=2HD=DF,则的值为( )
A.1 B.
C. D.
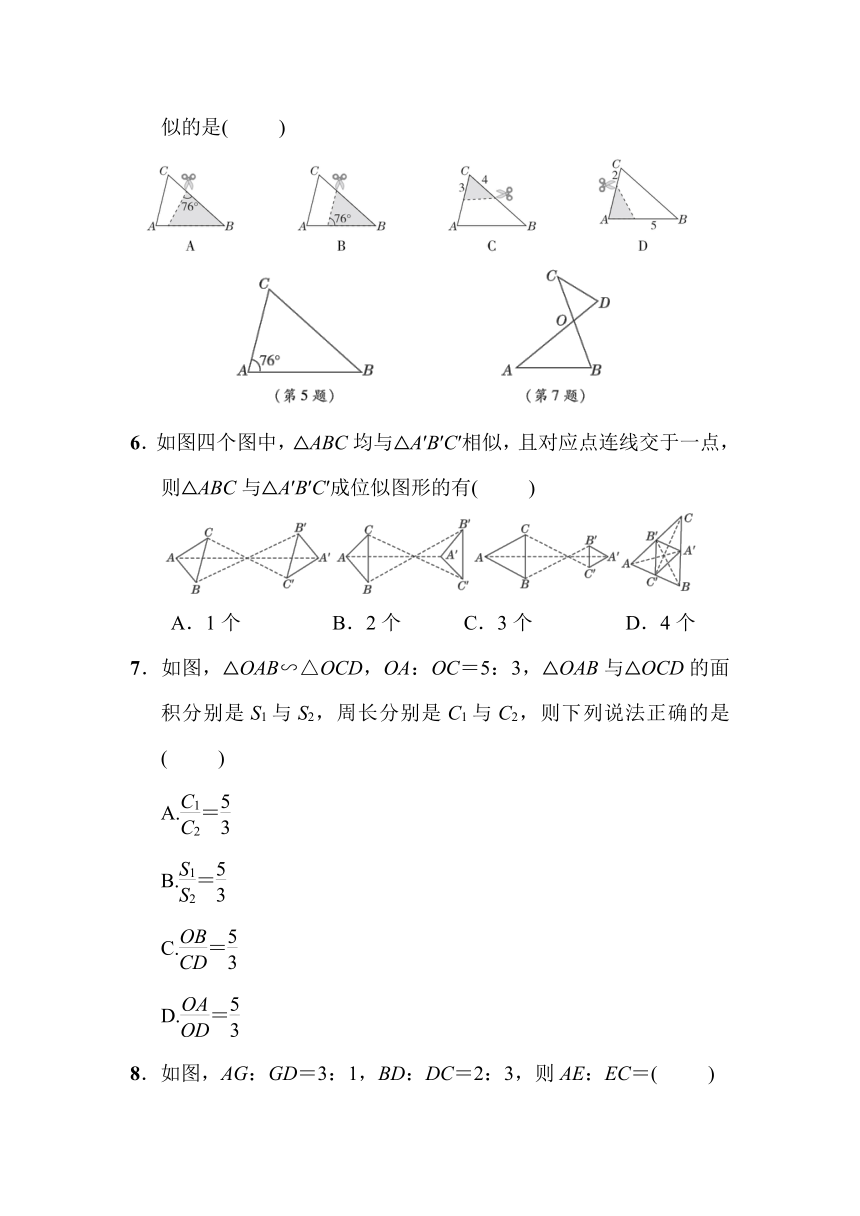
5.如图,△ABC中,∠A=76°,AB=8,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
6.如图四个图中,△ABC均与△A′B′C′相似,且对应点连线交于一点,则△ABC与△A′B′C′成位似图形的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,△OAB∽△OCD,OA:OC=5:3,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A.=
B.=
C.=
D.=
8.如图,AG:GD=3:1,BD:DC=2:3,则AE:EC=( )
A.8:7 B.8:5 C.3:2 D.6:5
9.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,翻折∠B,使点B落在直角边AC上某一点D处,折痕为EF,点E,F分别在边BC,AB上,若△CDE与△ABC相似,则CE的长为( )
A. B. C.或 D.或
10.如图,边长为4的正方形ABCD中,对角线AC,BD交于点O,E在线段OD上,连接CE,作EF⊥CE交AB于点F,连接CF交BD于点H,则下列结论:①EF=EC;②CF2=CG·CA;③BE·DH=16;④若BF=1,则DE=中,正确的是( )
A.①②④ B.①③④
C.①②③ D.①②③④
二、填空题(本大题共4小题,每小题5分,满分20分)
11.钓鱼岛列岛是我国最早发现、命名,并行使主权的群岛,在一幅比例尺是1:100 000的地图上,测得钓鱼岛的东西走向长为 3.6厘米,那么它的东西走向实际长大约为________千米.
12.如图,已知三个边长均为1的正方形拼成一个矩形ABCD,则 ∠AFE+∠ACE=________.
13.[母题:教材P72习题T1 ]已知==(xyz≠0),则的值为________.
14.如图,△ABC∽△ADE,∠BAC=∠DAE=90°,AB=9,AC=12,点D是线段BC上的动点,从点B运动到点C.请探究下列问题:
(1)当BD=2时,CE=________;
(2)设P为线段DE的中点,在点D的运动过程中,CP的最小值是________.
三、(本大题共2小题,每小题8分,满分16分)
15.已知a,b,c是△ABC的三边,且满足==, a+b+c=30,试判断△ABC的形状,并说明理由.
16.如图,AB∥CD,AD⊥BC于点O,OA=6,OD=9,BC=10,求CD的长.
四、(本大题共2小题,每小题8分,满分16分)
17.西安大雁塔作为现存最早、规模最大的唐代四方楼阁式砖塔,是佛塔这种古印度佛寺的建筑形式随佛教传入中原地区,并融入华夏文化的典型物证,是凝聚了中国古代劳动人民智慧结晶的标志性建筑.小明同学想利用所学数学知识来测量大雁塔的高度,如图,小明在点B处放置一个平面镜,站在A处恰好能从平面镜中看到塔的顶端D,此时测得小明到镜面的距离AB为2米,已知平面镜到塔底部中心的距离BC为86米,小明眼睛到地面的距离AE为1.5米,已知AE⊥AC,CD⊥AC,点A,B,C在一条水平线上.请你帮小明计算出大雁塔的高度CD.(平面镜的大小忽略不计)
18.如图,已知AE为∠BAC的平分线,ED∥CA,若BE=2,EC=3,AC=4,求AD的长.
五、(本大题共2小题,每小题10分,满分20分)
19.已知:△ABC三个顶点的坐标分别为A(2,2),B(4,1),C(1,5).
(1)以点O为位似中心,在第一象限将△ABC放大为原来的2倍,得到△A1B1C1,请在网格中画出△A1B1C1;
(2)若点P(x,y)是△ABC内任意一点,点P在△A1B1C1内的对应点为P1,则点P1的坐标为________;
(3)请用无刻度直尺将线段AB三等分.
20.阅读与计算:请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图①,在△ABC中,AD平分 ∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图②,过C作CE∥DA,交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图③,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是________.
六、(本题满分12分)
21.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于M,连接CM交DB于N.
(1)求证:BD2=AD·CD.
(2)若CD=6,AD=8,求DN的长.
七、(本题满分12分)
22.某课本中有一道作业题:有一块三角形余料ABC,如图①,它的边BC=12 m,高线AD=8 m.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长为多少米?小颖解得此题的答案为4.8 m.
(1)你知道小颖是怎么做的吗?请你写出解答过程.
(2)善于反思,她又提出了如下的问题,如果原题中所要加工的零件只是一个矩形,如图②,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
(3)如图③,如果将这块余料的形状改为Rt△ABC,已知∠A=90°,AB=8 m,AC=6 m,要把它加工成一个形状为平行四边形PQMN的工件,使QM在BC上,P,N两点分别在AB,AC上,且 PN=8 m,则平行四边形PQMN的面积为________m2.
八、(本题满分14分)
23. 定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图①,若四边形ABCD是以AC为“相似对角线”的四边形, AB=1,BC=2,∠ABC=∠ACD=90°,求CD的长.
(2)如图②,在四边形ABCD中,∠ABC=70°,∠ADC=145°,对角线BD平分∠ABC.请问BD是四边形ABCD的“相似对角线”吗?请说明理由;
(3)运用:如图③,已知FH是四边形EFGH的“相似对角线”,∠EFH=∠HFG=30°.连接EG,若△EFG的面积为8 ,求FH的长.
INCLUDEPICTURE"卷23.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 HK安徽\\卷23.EPS" \* MERGEFORMATINET 答案
一、1.B 2.A 3.A 4.B 5.C 6.C 7.A
8.D 【点拨】过点D作DF∥BE交AC于点F,
则==,==3,
∴AE:EC=6:5.
9.D 【点拨】∵∠C=90°,AC=3,BC=4,翻折∠B,使点B落在直角边AC上某一点D处,
∴AB=5,BE=DE,BE=4-CE.
当△CDE∽△CBA时,=,
∴=,解得CE=;
当△CDE∽△CAB时,=,
∴=,解得CE=.
综上可得,CE的长为或.
10.D 【点拨】连接AE.
∵四边形ABCD是边长为4的正方形,
∴AD=CD=AB=BC=4,∠ABC=∠BAD=∠BCD=90°,
∠ADB=∠CDB=∠BAC=∠DBC=∠ACD=45°.
又∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=EC,∠DAE=∠DCE,∴∠EAF=∠BCE.
∵EF⊥CE,∴∠FEC=90°.
∵∠ABC+∠FEC+∠EFB+∠BCE=360°,∠ABC=90°,
∴∠BCE+∠EFB=180°.
又∵∠AFE+∠BFE=180°,
∴∠AFE=∠BCE=∠EAF,∴AE=EF.
∵EC=AE,∴EF=EC,故①正确;
∵EF=EC,∠FEC=90°,
∴∠EFC=∠ECF=45°,∴∠FAC=∠EFC.
又∵∠ACF=∠FCG,
∴△FCG∽△ACF,∴=,
∴CF2=CG·CA,故②正确;
∵∠ECH=45°=∠CDB,∠EHC=∠DHC,
∴△ECH∽△CDH,∴=,∴=.
∵∠ECH=45°=∠DBC,∠BEC=∠CEH,
∴△ECH∽△EBC,
∴=,∴=,∴=,
∴BC·CD=BE·DH=16,故③正确;
∵BF=1,AB=BC=4,∠ABC=90°,
∴AF=3,AC=4.
∵∠ECF=∠ACD=45°,∴∠ACF=∠DCE.
又∵∠FAC=∠CDE=45°,
∴△AFC∽△DEC,∴=,∴=eq \r(2),
∴DE=eq \f(3,2),故④正确.
二、11.3.6
12.45° 【点拨】由题意得AE=eq \r(2),EF=1,EC=2,∠AEB=45°,
∴=eq \r(2),=eq \r(2),∴=.
∵∠AEF=∠AEC,∴△AEF∽△CEA,
∴∠AFE=∠CAE,
∴∠AFE+∠ACE=∠ACE+∠CAE=∠AEB=45°.
13.3或0 【点拨】∵==(xyz≠0),
∴设===k,
∴y+z=xk,z+x=yk,x+y=zk,
∴2x+2y+2z=xk+yk+zk,
∴2(x+y+z)=k(x+y+z).
分两种情况:
当x+y+z≠0时,k=2,∴x+z=2y,
∴==3;
当x+y+z=0时,=0.
综上所述,的值为3或0.
14.(1) (2)6 【点拨】(1)∵△ABC∽△ADE,
∴=,∴=.∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∴△BAD∽△CAE,∴==.
∵BD=2,∴CE=.
(2)∵△BAD∽△CAE,
∴∠ABD=∠ACE.
∵∠BAC=90°,∴∠ABD+∠ACB=90°,
∴∠ACB+∠ACE=90°,即∠DCE=90°.
∵P为DE的中点,∴CP=DE.
∵△ABC∽△ADE,
∴AD的值最小时,DE的值最小,此时CP的值最小.
∵AB=9,AC=12,∠BAC=90°,
∴BC===15.
根据垂线段最短可知,当AD⊥BC时,AD的值最小,此时AD==.
易知=,∴DE=12,
∴CP的最小值为×12=6.
三、15.【解】△ABC 是直角三角形,理由:
设===k,
则 a=3k-1,b=4k+4,c=8k-3.
∵ a+b+c=30,
∴3k-1+4k+4+8k-3=30,∴ k=2,
∴a=5,b=12,c=13,
∴b2+a2=c2,∴△ABC是直角三角形.
16.【解】∵AB∥CD,∴△ABO∽△DCO.
∴=,∴=,解得OC=6.
∵AD⊥BC,∴△COD为直角三角形,
∴OC2+OD2=CD2,
∴CD==3.
四、17.【解】由题意得∠EBA=∠DBC.
∵EA⊥AC,DC⊥AC,
∴∠EAB=∠DCB=90°,∴△DCB∽△EAB,
∴=,∴=,∴CD=64.5米,
∴大雁塔的高度CD为64.5米.
18.【解】∵AE为∠BAC的平分线,
∴∠DAE=∠EAC.
∵ED∥CA,∴∠DEA=∠EAC,
∴∠DAE=∠DEA,∴ED=AD.
∵ED∥CA,∴△BED∽△BCA,
∴=.
∵BE=2,EC=3,AC=4,
∴=,∴ED=,∴AD=.
五、19.【解】(1)如图,△A1B1C1即为所求.
(2)(2x,2y)
(3)如图,点G,H 将线段AB三等分.
20.(1)【证明】如题图②,过C作CE∥DA,交BA的延长线于E.
∵CE∥AD,
∴=,∠DAC=∠ACE,∠BAD=∠E.
∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠ACE=∠E,
∴AE=AC,∴=.
(2)eq \f(9+3, 5) 【点拨】∵AB=3,BC=4,∠ABC=90°,
∴AC=5.
∵AD平分∠BAC,
∴=,即=,∴BD=,
∴AD===eq \f(3,2),
∴△ABD的周长=+3+eq \f(3,2)=eq \f(9+3, 5).
六、 21.(1)【证明】∵DB平分∠ADC,∴∠ADB=∠CDB.
∵∠ABD=∠BCD=90°,∴△ABD∽△BCD,
∴=,∴BD2=AD·CD.
(2)【解】∵BM∥CD,∴∠MBD=∠CDB.
又∵∠MDB=∠CDB,∴∠MBD=∠MDB,
∴MB=MD.
∵∠ABD=90°,
∴∠A+∠ADB=90°,∠ABM+∠MBD=90°,
∴∠A=∠ABM,∴MA=MB,∴MB=AD=4.
∵BD2=AD·CD,CD=6,AD=8,
∴BD2=8×6=48,∴BD=4eq \r(3).
∵BM∥CD,∴==,
∴=,∴eq \f(4-DN, DN)=,∴DN=eq \f(12,3).
七、 22.【解】(1)∵四边形PQMN是正方形,
∴PN∥BC,∴△APN∽△ABC.
∵AD是△ABC的高线,∴AE是△APN的高线,
∴=.
设正方形零件的边长为tm.
∵BC=12m,AD=8m,∴AE=(8-t)m,
∴=,解得t=4.8,
∴加工成的正方形零件的边长为4.8m.
(2)设PN=xm,矩形PQMN的面积为Sm2.
由已知可得△APN∽△ABC,∴=.
易知DE=PQ,∴=,
解得PQ=8-x,
则S=PN·PQ=x(8-x)=-x2+8x=-(x-6)2+24.
∵-<0,∴当x=6时,S有最大值24,∴8-x=4.
答:当矩形面积达到最大值时,零件的两条边长分别为6m,4m.
(3)7.68
八、23.【解】(1)∵四边形ABCD是以AC为“相似对角线”的四边形,∠ABC=∠ACD=90°,
∴△ABC∽△ACD或△ABC∽△DCA.
在Rt△ABC中,AB=1,BC=2,由勾股定理得AC=eq \r(5).
当△ABC∽△ACD时,=,
∴eq \f(1, )=,∴CD=2.
当△ABC∽△DCA时,=,
∴=eq \f(2, ),∴CD=eq \f(,2).
综上,CD=2eq \r(5)或eq \f(,2).
(2)BD是四边形ABCD的“相似对角线”.理由如下:
∵BD平分∠ABC,
∴∠ABD=∠DBC=∠ABC=35°,
∴∠BAD+∠ADB=145°.
∵∠ADC=145°,∴∠BDC=∠BAD.
又∵∠ABD=∠DBC,
∴△BDC∽△BAD,
∴BD是四边形ABCD的“相似对角线”.
(3)作EQ⊥FG于Q.
∵FH是四边形EFGH的“相似对角线”,∠EFH=∠HFG,
∴△FEH∽△FHG,
∴=,∴FH2=EF·FG.
∵∠EFH=∠HFG=30°,∴∠EFQ=60°,
∴∠FEQ=30°,∴FQ=EF,
由勾股定理可得EQ=eq \f(,2)EF.
∵△EFG的面积为8,
∴·FG·EQ=×FG×eq \f(,2)EF=8eq \r(3),
∴FH2=32.
又∵FH>0,∴FH=4.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.有下列说法:①所有的等腰三角形都相似;②所有的等边三角形都相似;③所有的正方形都相似;④所有的矩形都相似,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.[母题:教材P69练习T3 ]若2x=5y(x,y≠0),则下列式子中错误的是( )
A.= B.= C.= D.=
3. 在设计人体雕像时,为了增加视觉美感,会使雕像上部(腰部以上)与下部(腰部以下)的高度比等于下部与全部的高度比等于(≈0.618,称为黄金分割比例),按此比例设计一座高度为2 m的雷锋雕像,那么该雕像的下部设计高度是( )
A.(-1)m B.(3-)m C.(-1)m D.(3-)m
4.[母题:教材P71练习T3 ]如图,AB∥CD∥EF,BE与AF相交于点H,且AH=2HD=DF,则的值为( )
A.1 B.
C. D.
5.如图,△ABC中,∠A=76°,AB=8,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
6.如图四个图中,△ABC均与△A′B′C′相似,且对应点连线交于一点,则△ABC与△A′B′C′成位似图形的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,△OAB∽△OCD,OA:OC=5:3,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A.=
B.=
C.=
D.=
8.如图,AG:GD=3:1,BD:DC=2:3,则AE:EC=( )
A.8:7 B.8:5 C.3:2 D.6:5
9.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,翻折∠B,使点B落在直角边AC上某一点D处,折痕为EF,点E,F分别在边BC,AB上,若△CDE与△ABC相似,则CE的长为( )
A. B. C.或 D.或
10.如图,边长为4的正方形ABCD中,对角线AC,BD交于点O,E在线段OD上,连接CE,作EF⊥CE交AB于点F,连接CF交BD于点H,则下列结论:①EF=EC;②CF2=CG·CA;③BE·DH=16;④若BF=1,则DE=中,正确的是( )
A.①②④ B.①③④
C.①②③ D.①②③④
二、填空题(本大题共4小题,每小题5分,满分20分)
11.钓鱼岛列岛是我国最早发现、命名,并行使主权的群岛,在一幅比例尺是1:100 000的地图上,测得钓鱼岛的东西走向长为 3.6厘米,那么它的东西走向实际长大约为________千米.
12.如图,已知三个边长均为1的正方形拼成一个矩形ABCD,则 ∠AFE+∠ACE=________.
13.[母题:教材P72习题T1 ]已知==(xyz≠0),则的值为________.
14.如图,△ABC∽△ADE,∠BAC=∠DAE=90°,AB=9,AC=12,点D是线段BC上的动点,从点B运动到点C.请探究下列问题:
(1)当BD=2时,CE=________;
(2)设P为线段DE的中点,在点D的运动过程中,CP的最小值是________.
三、(本大题共2小题,每小题8分,满分16分)
15.已知a,b,c是△ABC的三边,且满足==, a+b+c=30,试判断△ABC的形状,并说明理由.
16.如图,AB∥CD,AD⊥BC于点O,OA=6,OD=9,BC=10,求CD的长.
四、(本大题共2小题,每小题8分,满分16分)
17.西安大雁塔作为现存最早、规模最大的唐代四方楼阁式砖塔,是佛塔这种古印度佛寺的建筑形式随佛教传入中原地区,并融入华夏文化的典型物证,是凝聚了中国古代劳动人民智慧结晶的标志性建筑.小明同学想利用所学数学知识来测量大雁塔的高度,如图,小明在点B处放置一个平面镜,站在A处恰好能从平面镜中看到塔的顶端D,此时测得小明到镜面的距离AB为2米,已知平面镜到塔底部中心的距离BC为86米,小明眼睛到地面的距离AE为1.5米,已知AE⊥AC,CD⊥AC,点A,B,C在一条水平线上.请你帮小明计算出大雁塔的高度CD.(平面镜的大小忽略不计)
18.如图,已知AE为∠BAC的平分线,ED∥CA,若BE=2,EC=3,AC=4,求AD的长.
五、(本大题共2小题,每小题10分,满分20分)
19.已知:△ABC三个顶点的坐标分别为A(2,2),B(4,1),C(1,5).
(1)以点O为位似中心,在第一象限将△ABC放大为原来的2倍,得到△A1B1C1,请在网格中画出△A1B1C1;
(2)若点P(x,y)是△ABC内任意一点,点P在△A1B1C1内的对应点为P1,则点P1的坐标为________;
(3)请用无刻度直尺将线段AB三等分.
20.阅读与计算:请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图①,在△ABC中,AD平分 ∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图②,过C作CE∥DA,交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图③,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是________.
六、(本题满分12分)
21.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于M,连接CM交DB于N.
(1)求证:BD2=AD·CD.
(2)若CD=6,AD=8,求DN的长.
七、(本题满分12分)
22.某课本中有一道作业题:有一块三角形余料ABC,如图①,它的边BC=12 m,高线AD=8 m.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长为多少米?小颖解得此题的答案为4.8 m.
(1)你知道小颖是怎么做的吗?请你写出解答过程.
(2)善于反思,她又提出了如下的问题,如果原题中所要加工的零件只是一个矩形,如图②,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
(3)如图③,如果将这块余料的形状改为Rt△ABC,已知∠A=90°,AB=8 m,AC=6 m,要把它加工成一个形状为平行四边形PQMN的工件,使QM在BC上,P,N两点分别在AB,AC上,且 PN=8 m,则平行四边形PQMN的面积为________m2.
八、(本题满分14分)
23. 定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图①,若四边形ABCD是以AC为“相似对角线”的四边形, AB=1,BC=2,∠ABC=∠ACD=90°,求CD的长.
(2)如图②,在四边形ABCD中,∠ABC=70°,∠ADC=145°,对角线BD平分∠ABC.请问BD是四边形ABCD的“相似对角线”吗?请说明理由;
(3)运用:如图③,已知FH是四边形EFGH的“相似对角线”,∠EFH=∠HFG=30°.连接EG,若△EFG的面积为8 ,求FH的长.
INCLUDEPICTURE"卷23.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 HK安徽\\卷23.EPS" \* MERGEFORMATINET 答案
一、1.B 2.A 3.A 4.B 5.C 6.C 7.A
8.D 【点拨】过点D作DF∥BE交AC于点F,
则==,==3,
∴AE:EC=6:5.
9.D 【点拨】∵∠C=90°,AC=3,BC=4,翻折∠B,使点B落在直角边AC上某一点D处,
∴AB=5,BE=DE,BE=4-CE.
当△CDE∽△CBA时,=,
∴=,解得CE=;
当△CDE∽△CAB时,=,
∴=,解得CE=.
综上可得,CE的长为或.
10.D 【点拨】连接AE.
∵四边形ABCD是边长为4的正方形,
∴AD=CD=AB=BC=4,∠ABC=∠BAD=∠BCD=90°,
∠ADB=∠CDB=∠BAC=∠DBC=∠ACD=45°.
又∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=EC,∠DAE=∠DCE,∴∠EAF=∠BCE.
∵EF⊥CE,∴∠FEC=90°.
∵∠ABC+∠FEC+∠EFB+∠BCE=360°,∠ABC=90°,
∴∠BCE+∠EFB=180°.
又∵∠AFE+∠BFE=180°,
∴∠AFE=∠BCE=∠EAF,∴AE=EF.
∵EC=AE,∴EF=EC,故①正确;
∵EF=EC,∠FEC=90°,
∴∠EFC=∠ECF=45°,∴∠FAC=∠EFC.
又∵∠ACF=∠FCG,
∴△FCG∽△ACF,∴=,
∴CF2=CG·CA,故②正确;
∵∠ECH=45°=∠CDB,∠EHC=∠DHC,
∴△ECH∽△CDH,∴=,∴=.
∵∠ECH=45°=∠DBC,∠BEC=∠CEH,
∴△ECH∽△EBC,
∴=,∴=,∴=,
∴BC·CD=BE·DH=16,故③正确;
∵BF=1,AB=BC=4,∠ABC=90°,
∴AF=3,AC=4.
∵∠ECF=∠ACD=45°,∴∠ACF=∠DCE.
又∵∠FAC=∠CDE=45°,
∴△AFC∽△DEC,∴=,∴=eq \r(2),
∴DE=eq \f(3,2),故④正确.
二、11.3.6
12.45° 【点拨】由题意得AE=eq \r(2),EF=1,EC=2,∠AEB=45°,
∴=eq \r(2),=eq \r(2),∴=.
∵∠AEF=∠AEC,∴△AEF∽△CEA,
∴∠AFE=∠CAE,
∴∠AFE+∠ACE=∠ACE+∠CAE=∠AEB=45°.
13.3或0 【点拨】∵==(xyz≠0),
∴设===k,
∴y+z=xk,z+x=yk,x+y=zk,
∴2x+2y+2z=xk+yk+zk,
∴2(x+y+z)=k(x+y+z).
分两种情况:
当x+y+z≠0时,k=2,∴x+z=2y,
∴==3;
当x+y+z=0时,=0.
综上所述,的值为3或0.
14.(1) (2)6 【点拨】(1)∵△ABC∽△ADE,
∴=,∴=.∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∴△BAD∽△CAE,∴==.
∵BD=2,∴CE=.
(2)∵△BAD∽△CAE,
∴∠ABD=∠ACE.
∵∠BAC=90°,∴∠ABD+∠ACB=90°,
∴∠ACB+∠ACE=90°,即∠DCE=90°.
∵P为DE的中点,∴CP=DE.
∵△ABC∽△ADE,
∴AD的值最小时,DE的值最小,此时CP的值最小.
∵AB=9,AC=12,∠BAC=90°,
∴BC===15.
根据垂线段最短可知,当AD⊥BC时,AD的值最小,此时AD==.
易知=,∴DE=12,
∴CP的最小值为×12=6.
三、15.【解】△ABC 是直角三角形,理由:
设===k,
则 a=3k-1,b=4k+4,c=8k-3.
∵ a+b+c=30,
∴3k-1+4k+4+8k-3=30,∴ k=2,
∴a=5,b=12,c=13,
∴b2+a2=c2,∴△ABC是直角三角形.
16.【解】∵AB∥CD,∴△ABO∽△DCO.
∴=,∴=,解得OC=6.
∵AD⊥BC,∴△COD为直角三角形,
∴OC2+OD2=CD2,
∴CD==3.
四、17.【解】由题意得∠EBA=∠DBC.
∵EA⊥AC,DC⊥AC,
∴∠EAB=∠DCB=90°,∴△DCB∽△EAB,
∴=,∴=,∴CD=64.5米,
∴大雁塔的高度CD为64.5米.
18.【解】∵AE为∠BAC的平分线,
∴∠DAE=∠EAC.
∵ED∥CA,∴∠DEA=∠EAC,
∴∠DAE=∠DEA,∴ED=AD.
∵ED∥CA,∴△BED∽△BCA,
∴=.
∵BE=2,EC=3,AC=4,
∴=,∴ED=,∴AD=.
五、19.【解】(1)如图,△A1B1C1即为所求.
(2)(2x,2y)
(3)如图,点G,H 将线段AB三等分.
20.(1)【证明】如题图②,过C作CE∥DA,交BA的延长线于E.
∵CE∥AD,
∴=,∠DAC=∠ACE,∠BAD=∠E.
∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠ACE=∠E,
∴AE=AC,∴=.
(2)eq \f(9+3, 5) 【点拨】∵AB=3,BC=4,∠ABC=90°,
∴AC=5.
∵AD平分∠BAC,
∴=,即=,∴BD=,
∴AD===eq \f(3,2),
∴△ABD的周长=+3+eq \f(3,2)=eq \f(9+3, 5).
六、 21.(1)【证明】∵DB平分∠ADC,∴∠ADB=∠CDB.
∵∠ABD=∠BCD=90°,∴△ABD∽△BCD,
∴=,∴BD2=AD·CD.
(2)【解】∵BM∥CD,∴∠MBD=∠CDB.
又∵∠MDB=∠CDB,∴∠MBD=∠MDB,
∴MB=MD.
∵∠ABD=90°,
∴∠A+∠ADB=90°,∠ABM+∠MBD=90°,
∴∠A=∠ABM,∴MA=MB,∴MB=AD=4.
∵BD2=AD·CD,CD=6,AD=8,
∴BD2=8×6=48,∴BD=4eq \r(3).
∵BM∥CD,∴==,
∴=,∴eq \f(4-DN, DN)=,∴DN=eq \f(12,3).
七、 22.【解】(1)∵四边形PQMN是正方形,
∴PN∥BC,∴△APN∽△ABC.
∵AD是△ABC的高线,∴AE是△APN的高线,
∴=.
设正方形零件的边长为tm.
∵BC=12m,AD=8m,∴AE=(8-t)m,
∴=,解得t=4.8,
∴加工成的正方形零件的边长为4.8m.
(2)设PN=xm,矩形PQMN的面积为Sm2.
由已知可得△APN∽△ABC,∴=.
易知DE=PQ,∴=,
解得PQ=8-x,
则S=PN·PQ=x(8-x)=-x2+8x=-(x-6)2+24.
∵-<0,∴当x=6时,S有最大值24,∴8-x=4.
答:当矩形面积达到最大值时,零件的两条边长分别为6m,4m.
(3)7.68
八、23.【解】(1)∵四边形ABCD是以AC为“相似对角线”的四边形,∠ABC=∠ACD=90°,
∴△ABC∽△ACD或△ABC∽△DCA.
在Rt△ABC中,AB=1,BC=2,由勾股定理得AC=eq \r(5).
当△ABC∽△ACD时,=,
∴eq \f(1, )=,∴CD=2.
当△ABC∽△DCA时,=,
∴=eq \f(2, ),∴CD=eq \f(,2).
综上,CD=2eq \r(5)或eq \f(,2).
(2)BD是四边形ABCD的“相似对角线”.理由如下:
∵BD平分∠ABC,
∴∠ABD=∠DBC=∠ABC=35°,
∴∠BAD+∠ADB=145°.
∵∠ADC=145°,∴∠BDC=∠BAD.
又∵∠ABD=∠DBC,
∴△BDC∽△BAD,
∴BD是四边形ABCD的“相似对角线”.
(3)作EQ⊥FG于Q.
∵FH是四边形EFGH的“相似对角线”,∠EFH=∠HFG,
∴△FEH∽△FHG,
∴=,∴FH2=EF·FG.
∵∠EFH=∠HFG=30°,∴∠EFQ=60°,
∴∠FEQ=30°,∴FQ=EF,
由勾股定理可得EQ=eq \f(,2)EF.
∵△EFG的面积为8,
∴·FG·EQ=×FG×eq \f(,2)EF=8eq \r(3),
∴FH2=32.
又∵FH>0,∴FH=4.
