初中数学沪科版九年级上册 第23章 解直角三角形 综合素质评价(含答案)
文档属性
| 名称 | 初中数学沪科版九年级上册 第23章 解直角三角形 综合素质评价(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 533.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 15:08:47 | ||
图片预览



文档简介
第23章 解直角三角形 综合素质评价
一、选择题(本大题共10小题,每小题4分,满分40分)
1.[2024·合肥市蜀山区模拟]已知实数a=tan 30°,b=sin 45°,c=cos 60°,则下列说法正确的是( )
A.b>a>c B.a>b>c C.b>c>a D.a>c>b
2.[母题:教材P114例1]如图,在Rt△ABC中,AC=4,BC=3, ∠C=90°,则sin A的值为( )
A. B. C. D.
3.在Rt△ABC中,∠B=90°,AB=2BC,则cos A的值为( )
A. B. C. D.2
4.如图,在平面直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点A的坐标为(0,3),tan∠ABO=,则菱形ABCD的周长为( )
A.6 B.6 C.12 D.8
5.[易错题]若α,β是一个三角形的两个锐角,且满足|sin α-|+(-tan β)2=0,则此三角形的形状是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
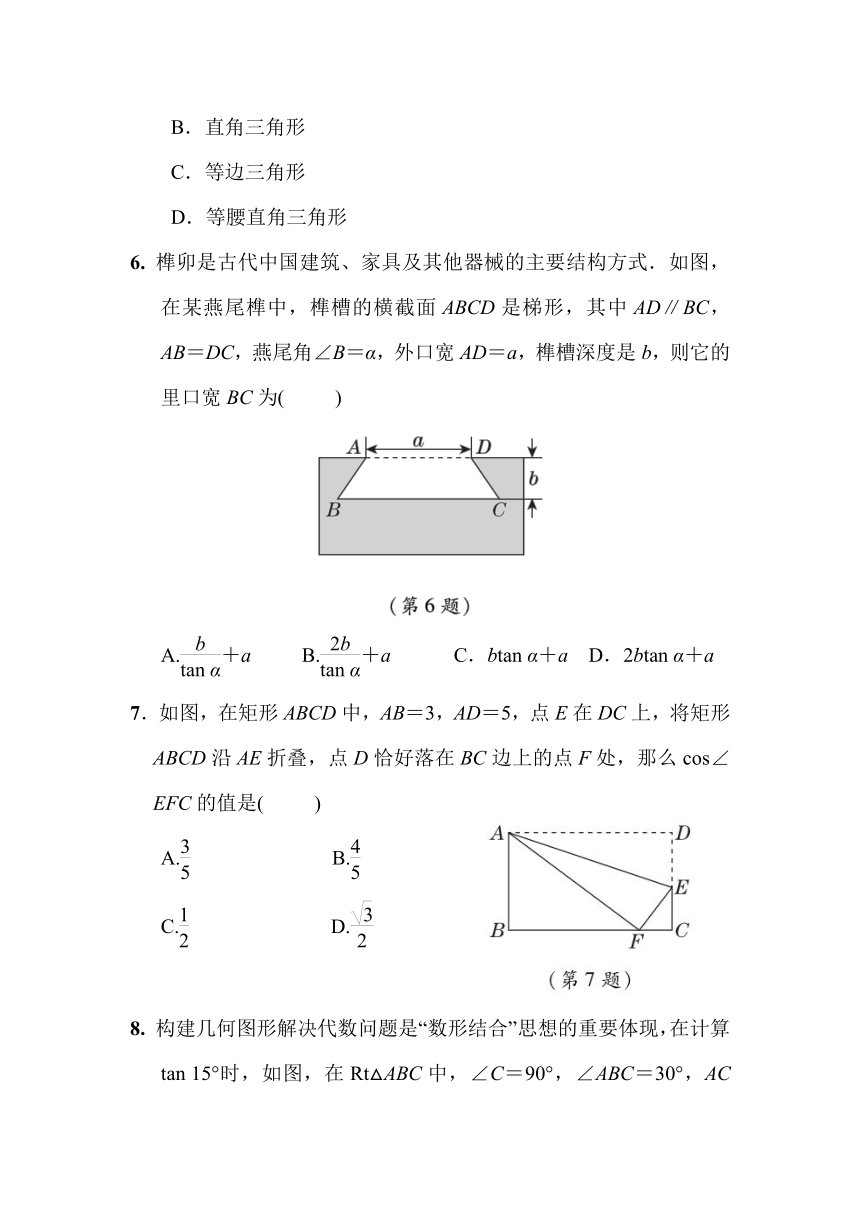
6. 榫卯是古代中国建筑、家具及其他器械的主要结构方式.如图,在某燕尾榫中,榫槽的横截面ABCD是梯形,其中AD∥BC, AB=DC,燕尾角∠B=α,外口宽AD=a,榫槽深度是b,则它的里口宽BC为( )
A.+a B.+a C.btan α+a D.2btan α+a
7.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是( )
A. B.
C. D.
8. 构建几何图形解决代数问题是“数形结合”思想的重要体现,在计算tan 15°时,如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,延长CB使BD=AB,连接AD,得∠D=15°,所以tan 15°====2-.类比这种方法,则tan 22.5°的值为( )
A.+1 B. C.-1 D.
9.如图,在△ABC中,AB=AC,BC=8,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则x与y满足的关系式为( )
A.x-y2=3 B.2x-y2=6 C.3x-y2=9 D.4x-y2=12
10.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,D为AC上任意一点,F为AB的中点,连接BD,E在BD上且∠BEC=90°,连接EF,则EF的最小值为( )
A. B.2 -3 C.3 -3 D.3
二、填空题(本大题共4小题,每小题5分,满分20分)
11.位于北京市石景山区首钢老工业园区北区的“首钢滑雪大跳台”巧妙地融入了敦煌壁画“飞天”元素.如图,赛道剖面图的一部分可抽象为线段AB.已知坡AB的长为50 m,坡AB的坡比为3:4,则铅直高度AH为________m.
12.[母题:教材P119练习T2]已知α,β为锐角,且α+β=90°, cos β=0.76,则sin α=________.
13.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度为i=1:3,且O,A,B在同一条直线上,则此人所在位置点P的铅直高度为________米.
14.利用科普书上的有关公式,发现锐角三角函数存在这样的公式:若α,β为锐角且α+β≠90°,则tan(α+β)=.
如:tan 75°=tan(30°+45°)==eq \f(eq \f(,3)+1, 1-eq \f(,3))=2+eq \r(3).利用此公式求解下列问题:
(1)若∠A,∠B为锐角且∠A+∠B=45°,则(1+tan A)(1+tan B)=________;
(2)(1+tan 1°)(1+tan 2°)(1+tan 3°)…(1+tan 43°)(1+tan 44°)=________.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:sin 45°-2cos 30°+ .
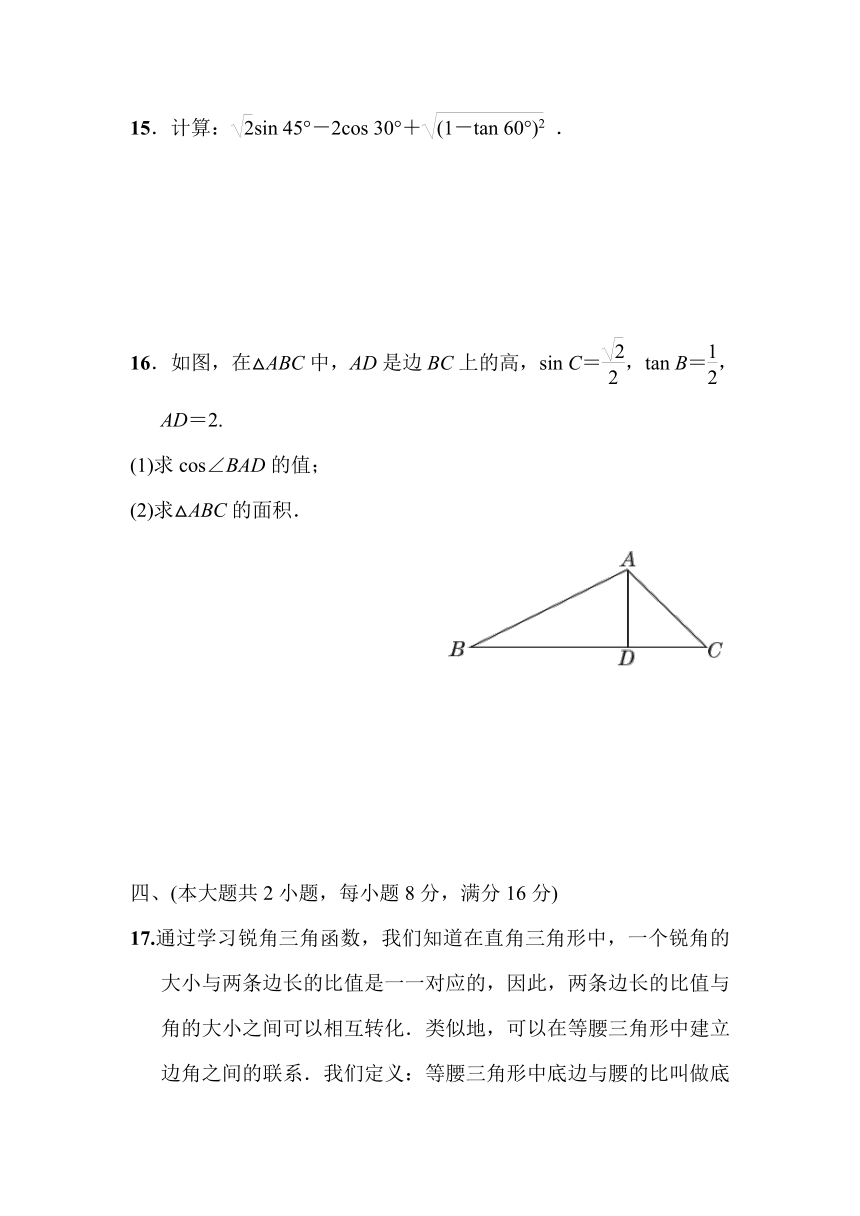
16.如图,在△ABC中,AD是边BC上的高,sin C=eq \f(,2),tan B=,AD=2.
(1)求cos∠BAD的值;
(2)求△ABC的面积.
四、(本大题共2小题,每小题8分,满分16分)
17.通过学习锐角三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似地,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图①,在△ABC中,AB=AC,底角∠B的邻对记作can B,这时can B==,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解答下列问题:
(1)can 30°=________;
(2)如图②,已知在△ABC中,AB=AC,can B=,S△ABC=24,求△ABC的周长.
18.自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图①所示的坡路进行改造.如图②所示,改造前的斜坡AB=200 m,坡度为1:.将斜坡AB的高度AE降低AC=20 m后,斜坡AB改造为斜坡CD,其坡度为1:4,求斜坡CD的长.(结果保留根号)
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)若AD∥BC(D为格点),连接CD,则线段CD的长为________;
(2)请你在△ABC的三个内角中任选一个锐角,若你所选的锐角是________,则它所对应的正弦函数值是________;
(3)若E为BC的中点,则tan∠CAE的值是________.
20.如图,△ABC中,BA=BC=13,AC=10,∠ABC的平分线与边AC交于点F,与△ABC的外角∠ACD的平分线交于点E.
(1)求sin A的值;
(2)求点E到直线BD的距离.
六、(本题满分12分)
21.我国首艘国产航母山东舰是保障国土安全,维护祖国统一的又一利器.如图,一架歼-15舰载机在航母正后方A点准备降落,此时在A测得航母舰首B的俯角为11.3°,舰尾C的俯角为14°,如果航母长为315米,且B比C高出10米,求舰载机相对航母舰尾C的高度.(参考数据:sin 11.3°≈0.20,sin 14°≈0.24,tan 11.3°≈0.20,tan 14°≈0.25)
七、(本题满分12分)
22.北斗卫星导航系统是中国自行研制的全球卫星导航系统,其由空间段、地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务.如图,小敏一家自驾到风景区C游玩,到达A地后,导航显示车辆应沿北偏西45°方向行驶10千米至B地,再沿北偏东60°方向行驶一段距离到达风景区C,小敏发现风景区C在A地的北偏东15°方向.
(1)求∠C的度数;
(2)求B,C两地间的距离.(如果运算结果有根号,请保留根号)
八、(本题满分14分)
23.阅读下列材料,解决后面的问题:
我们知道,三角形的面积等于二分之一底乘高.在学习了三角函数后,还可以这样求三角形的面积:对于△ABC,a,b,c分别为∠A,∠B,∠C的对边,则其面积S=absin C=bcsin A=casin B.
(1)如图①,在△ABC中,∠A=30°,b=2,c=3,求△ABC的面积;
(2)如图②,在△ABC中,已知AB=2,BC=1,D为AC上一点,求证:BD=;
(3)正数a,b,c,d,e,f满足a+b=c+d=e+f=1,求证:af+bc+de<1.
INCLUDEPICTURE"卷期末.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 HK安徽\\卷期末.EPS" \* MERGEFORMATINET
答案
一、1.A 2.D 3.A
4.D 【点拨】∵点A的坐标为(0,3),
∴AO=3.
∵tan∠ABO=eq \r(3),∠AOB=90°,
∴=eq \r(3),∴=eq \r(3),∴BO=eq \r(3).
∴AB==eq \r(32+()2) ==2eq \r(3).
∵菱形的四条边相等,
∴菱形ABCD的周长为2eq \r(3)×4=8eq \r(3).
5.C 【点拨】∵|sin α-eq \f(,2)|+(eq \r(3)-tan β)2=0,
∴sin α-eq \f(,2)=0,eq \r(3)-tanβ=0,
∴sin α=eq \f(,2),tan β=eq \r(3).
又∵α,β都是锐角,∴α=60°,β=60°,
∴此三角形的形状是等边三角形.
[点易错] 本题求出α,β后,很容易给出结论是等腰三角形.但第三个角也是60°,所以是等边三角形.类比:△ABC的两个内角∠A=45°,∠B=45°,△ABC是等腰直角三角形.
6.B 【点拨】如图,过点A,D分别作BC的垂线段,垂足分别为E,F.
易得∠DCB=∠B=α,EF=AD=a,AE=DF=b.
在Rt△AEB中,BE==,
在Rt△DFC,CF==,
∴BC=BE+EF+FC=+a+=+a.
7.A 【点拨】∵四边形ABCD为矩形,
∴AD=BC=5,AB=CD=3,∠B=∠C=90°.
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=5,EF=DE.
在Rt△ABF中,∵BF==4,
∴CF=BC-BF=5-4=1.
设CE=x,则DE=EF=3-x.
在Rt△ECF中,∵CE2+FC2=EF2,
∴x2+12=(3-x)2,解得x=,
∴EF=3-x=,∴cos∠EFC==.
8.C 【点拨】如图所示,在Rt△ABC中,∠C=90°,∠ABC=45°,延长CB使BD=AB,连接AD,得∠D=22.5°.
设AC=BC=1,则AB=BD=eq \r(2),
∴tan 22.5°===eq \r(2)-1.
9.C 【点拨】过A作AQ⊥BC于Q,过E作EM⊥BC于M,连接DE.
∵AB=AC,BC=8,tan∠ACB=y,
∴==y,CQ=4,
∴AQ=4y.
∵BE的垂直平分线交BC于D,BD=x,
∴BD=DE=x.
∵AQ⊥BC,EM⊥BC,∴AQ∥EM.
又∵E为AC的中点,
∴MC=CQ=2,∴EM=2y,DM=8-2-x=6-x.
在Rt△EDM中,由勾股定理得
x2=(2y)2+(6-x)2,即3x-y2=9.
10.C 【点拨】取BC的中点Q,连接EQ,FQ.
∵F为AB的中点,∴FQ=AC.
∵∠ACB=90°,∠A=30°,BC=6,
∴AC==eq \f(6, eq \f(,3))=6eq \r(3),∴FQ=3eq \r(3).
∵∠BEC=90°,Q为BC的中点,∴EQ=BC=3.
当E,F,Q三点共线时,EF的值最小,
∴EF=FQ-EQ=3eq \r(3)-3.
二、11.30 12.0.76
13.(25eq \r(3)-25) 【点拨】作PE⊥OB于点E,PF⊥CO于点F.
在Rt△AOC中,AO=100米,∠CAO=60°,
∴CO=AO·tan 60°=100eq \r(3)米.
设PE=x米,易知FO=x米.
∵=,∴AE=3x米.
在Rt△PCF中,∠CPF=45°,CF=(100eq \r(3)-x)米,
PF=OE=OA+AE=(100+3x)米.
∴PF=CF,∴100+3x=100eq \r(3)-x,
解得x=25eq \r(3)-25.∴PE=(25eq \r(3)-25)米.
14.(1)2 (2)222
【点拨】(1)当∠A+∠B=45°时,tan(∠A+∠B)==1,即tan A+tan B=1-tan Atan B,
∴(1+tan A)(1+tan B)=1+tan A+tan B+tan Atan B=1+1-tan Atan B+tan Atan B=2.
(2)由(1)可知(1+tan 1°)(1+tan 44°)=(1+tan 2°)(1+tan 43°)=…=2,∴原式=222.
三、15.【解】原式=×-2×+
=1-eq \r(3)+(tan 60°-1)
=1-eq \r(3)+eq \r(3)-1=0.
16.【解】(1)在Rt△ABD中,tan B==,AD=2,
∴BD=4,∴AB==2,
∴cos∠BAD==.
(2)∵sin C=,∴∠C=45°,
∴tan C==1,
∴CD=2,∴BC=BD+CD=6,
∴S△ABC=×AD·BC=6.
四、17.【解】(1)
(2)过点A作AE⊥BC于点E.
∵can B=,∴可设BC=8x,则AC=5x=AB.
易知BE=4x,
∴AE==3x.
∵S△ABC=24,
∴BC·AE=12x2=24,解得x=(负值已舍去),
故AB=AC=5eq \r(2),BC=8eq \r(2).
∴△ABC的周长=5eq \r(2)+5eq \r(2)+8eq \r(2)=18eq \r(2).
18.【解】∵∠AEB=90°,AB=200m,斜坡AB的坡度为 1:,
∴tan∠ABE===,∴∠ABE=30°,
∴AE=AB=100m.
∵AC=20m,∴CE=80m.
∵∠CED=90°,斜坡CD的坡度为1?4,
∴=,即=,
∴ED=320m.
∴CD==80(m).
∴斜坡CD的长是80m.
五、19.【解】(1) (2)∠ACB;(答案不唯一)
【点拨】利用网格构造直角三角形易得AB=,AC=2 ,BC=5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
∴sin∠ACB==.
(3)
20.【解】(1)∵AB=BC=13,AC=10,∠ABC的平分线与边AC交于点F,
∴∠ABF=∠FBC,BF⊥AC,AF=5.
在Rt△ABF中,BF==12.
∴sin A==.
(2)过点E作EG⊥BD,垂足为G.
∵CE平分∠ACD,EF⊥AC,EG⊥BD,
∴EF=EG.
在Rt△ABF中,sin∠ABF==.
在Rt△EBG中,sin∠EBG=sin∠ABF===,
BF=12,∴EG=.
∴点E到直线BD的距离是.
六、21.【解】设过A,B,C的水平线分别为AP,BM,CN,过A作AD⊥BM于D,交CN于E,则DE=10米,∠BAP=11.3°,∠PAC=14°,AP∥BM∥CN,
∴∠ABD=∠BAP=11.3°,∠ACE=∠PAC=14°.
设AE=x米,则AD=AE-DE=(x-10)米.
在Rt△ABD中,tan∠ABD==tan 11.3°≈0.20,
∴BD≈5AD=5(x-10)米.
在Rt△ACE中,tan∠ACE==tan 14°≈0.25,
∴CE≈4AE=4x米.
易知BD-CE=315米,
∴5(x-10)-4x≈315,
解得x≈365,即AE≈365米,
∴舰载机相对航母舰尾C的高度约为365米.
七、22.【解】(1)如图.由题意得∠BAD=45°,∠DAC=15°,∠FBC=60°,EF∥DA,
∴∠ABE=∠BAD=45°,
∴∠ABC=180°-∠ABE-∠FBC=75°.
∵∠BAC=∠BAD+∠DAC=60°,
∴∠C=180°-∠BAC-∠ABC=45°.
(2)如图,过点B作BG⊥AC,垂足为G.
在Rt△ABG中,AB=10千米,∠BAG=60°,
∴BG=AB·sin 60°=10×eq \f(,2)=5eq \r(3) (千米).
在Rt△BGC中,∠C=45°,
∴BC==eq \f(5eq \r(3),eq \f(,2))=5 (千米),
∴B,C两地间的距离为5eq \r(6)千米.
八、23.(1)【解】由面积公式可知S△ABC=bcsin A =bcsin 30°=
×2×3×=.
(2)【证明】∵S△ABC=S△ABD+S△BCD,
∴AB·BD·sin∠1+BC·BD·sin∠2=AB·BC·sin(∠1+∠2),
∴2BD·sin∠1+BD·sin∠2=2sin(∠1+∠2),
∴BD=.
(3)【证明】如图,作边长为1的等边三角形ABC,点D,E,F分别在AB,BC,AC上,且AD=a,BD=b,BE=c,EC=d,
CF=e,AF=f,则∠A=∠B=∠C=60°.
∵S△ADF+S△BDE+S△CEF<S△ABC,
∴af·sin 60°+bc·sin 60°+de·sin 60°∴af+bc+de<1.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.[2024·合肥市蜀山区模拟]已知实数a=tan 30°,b=sin 45°,c=cos 60°,则下列说法正确的是( )
A.b>a>c B.a>b>c C.b>c>a D.a>c>b
2.[母题:教材P114例1]如图,在Rt△ABC中,AC=4,BC=3, ∠C=90°,则sin A的值为( )
A. B. C. D.
3.在Rt△ABC中,∠B=90°,AB=2BC,则cos A的值为( )
A. B. C. D.2
4.如图,在平面直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点A的坐标为(0,3),tan∠ABO=,则菱形ABCD的周长为( )
A.6 B.6 C.12 D.8
5.[易错题]若α,β是一个三角形的两个锐角,且满足|sin α-|+(-tan β)2=0,则此三角形的形状是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
6. 榫卯是古代中国建筑、家具及其他器械的主要结构方式.如图,在某燕尾榫中,榫槽的横截面ABCD是梯形,其中AD∥BC, AB=DC,燕尾角∠B=α,外口宽AD=a,榫槽深度是b,则它的里口宽BC为( )
A.+a B.+a C.btan α+a D.2btan α+a
7.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是( )
A. B.
C. D.
8. 构建几何图形解决代数问题是“数形结合”思想的重要体现,在计算tan 15°时,如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,延长CB使BD=AB,连接AD,得∠D=15°,所以tan 15°====2-.类比这种方法,则tan 22.5°的值为( )
A.+1 B. C.-1 D.
9.如图,在△ABC中,AB=AC,BC=8,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则x与y满足的关系式为( )
A.x-y2=3 B.2x-y2=6 C.3x-y2=9 D.4x-y2=12
10.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,D为AC上任意一点,F为AB的中点,连接BD,E在BD上且∠BEC=90°,连接EF,则EF的最小值为( )
A. B.2 -3 C.3 -3 D.3
二、填空题(本大题共4小题,每小题5分,满分20分)
11.位于北京市石景山区首钢老工业园区北区的“首钢滑雪大跳台”巧妙地融入了敦煌壁画“飞天”元素.如图,赛道剖面图的一部分可抽象为线段AB.已知坡AB的长为50 m,坡AB的坡比为3:4,则铅直高度AH为________m.
12.[母题:教材P119练习T2]已知α,β为锐角,且α+β=90°, cos β=0.76,则sin α=________.
13.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度为i=1:3,且O,A,B在同一条直线上,则此人所在位置点P的铅直高度为________米.
14.利用科普书上的有关公式,发现锐角三角函数存在这样的公式:若α,β为锐角且α+β≠90°,则tan(α+β)=.
如:tan 75°=tan(30°+45°)==eq \f(eq \f(,3)+1, 1-eq \f(,3))=2+eq \r(3).利用此公式求解下列问题:
(1)若∠A,∠B为锐角且∠A+∠B=45°,则(1+tan A)(1+tan B)=________;
(2)(1+tan 1°)(1+tan 2°)(1+tan 3°)…(1+tan 43°)(1+tan 44°)=________.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:sin 45°-2cos 30°+ .
16.如图,在△ABC中,AD是边BC上的高,sin C=eq \f(,2),tan B=,AD=2.
(1)求cos∠BAD的值;
(2)求△ABC的面积.
四、(本大题共2小题,每小题8分,满分16分)
17.通过学习锐角三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似地,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图①,在△ABC中,AB=AC,底角∠B的邻对记作can B,这时can B==,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解答下列问题:
(1)can 30°=________;
(2)如图②,已知在△ABC中,AB=AC,can B=,S△ABC=24,求△ABC的周长.
18.自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图①所示的坡路进行改造.如图②所示,改造前的斜坡AB=200 m,坡度为1:.将斜坡AB的高度AE降低AC=20 m后,斜坡AB改造为斜坡CD,其坡度为1:4,求斜坡CD的长.(结果保留根号)
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)若AD∥BC(D为格点),连接CD,则线段CD的长为________;
(2)请你在△ABC的三个内角中任选一个锐角,若你所选的锐角是________,则它所对应的正弦函数值是________;
(3)若E为BC的中点,则tan∠CAE的值是________.
20.如图,△ABC中,BA=BC=13,AC=10,∠ABC的平分线与边AC交于点F,与△ABC的外角∠ACD的平分线交于点E.
(1)求sin A的值;
(2)求点E到直线BD的距离.
六、(本题满分12分)
21.我国首艘国产航母山东舰是保障国土安全,维护祖国统一的又一利器.如图,一架歼-15舰载机在航母正后方A点准备降落,此时在A测得航母舰首B的俯角为11.3°,舰尾C的俯角为14°,如果航母长为315米,且B比C高出10米,求舰载机相对航母舰尾C的高度.(参考数据:sin 11.3°≈0.20,sin 14°≈0.24,tan 11.3°≈0.20,tan 14°≈0.25)
七、(本题满分12分)
22.北斗卫星导航系统是中国自行研制的全球卫星导航系统,其由空间段、地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务.如图,小敏一家自驾到风景区C游玩,到达A地后,导航显示车辆应沿北偏西45°方向行驶10千米至B地,再沿北偏东60°方向行驶一段距离到达风景区C,小敏发现风景区C在A地的北偏东15°方向.
(1)求∠C的度数;
(2)求B,C两地间的距离.(如果运算结果有根号,请保留根号)
八、(本题满分14分)
23.阅读下列材料,解决后面的问题:
我们知道,三角形的面积等于二分之一底乘高.在学习了三角函数后,还可以这样求三角形的面积:对于△ABC,a,b,c分别为∠A,∠B,∠C的对边,则其面积S=absin C=bcsin A=casin B.
(1)如图①,在△ABC中,∠A=30°,b=2,c=3,求△ABC的面积;
(2)如图②,在△ABC中,已知AB=2,BC=1,D为AC上一点,求证:BD=;
(3)正数a,b,c,d,e,f满足a+b=c+d=e+f=1,求证:af+bc+de<1.
INCLUDEPICTURE"卷期末.EPS" INCLUDEPICTURE \d "D:\\0\\初中\\24秋 典中点 9 数学 HK安徽\\卷期末.EPS" \* MERGEFORMATINET
答案
一、1.A 2.D 3.A
4.D 【点拨】∵点A的坐标为(0,3),
∴AO=3.
∵tan∠ABO=eq \r(3),∠AOB=90°,
∴=eq \r(3),∴=eq \r(3),∴BO=eq \r(3).
∴AB==eq \r(32+()2) ==2eq \r(3).
∵菱形的四条边相等,
∴菱形ABCD的周长为2eq \r(3)×4=8eq \r(3).
5.C 【点拨】∵|sin α-eq \f(,2)|+(eq \r(3)-tan β)2=0,
∴sin α-eq \f(,2)=0,eq \r(3)-tanβ=0,
∴sin α=eq \f(,2),tan β=eq \r(3).
又∵α,β都是锐角,∴α=60°,β=60°,
∴此三角形的形状是等边三角形.
[点易错] 本题求出α,β后,很容易给出结论是等腰三角形.但第三个角也是60°,所以是等边三角形.类比:△ABC的两个内角∠A=45°,∠B=45°,△ABC是等腰直角三角形.
6.B 【点拨】如图,过点A,D分别作BC的垂线段,垂足分别为E,F.
易得∠DCB=∠B=α,EF=AD=a,AE=DF=b.
在Rt△AEB中,BE==,
在Rt△DFC,CF==,
∴BC=BE+EF+FC=+a+=+a.
7.A 【点拨】∵四边形ABCD为矩形,
∴AD=BC=5,AB=CD=3,∠B=∠C=90°.
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=5,EF=DE.
在Rt△ABF中,∵BF==4,
∴CF=BC-BF=5-4=1.
设CE=x,则DE=EF=3-x.
在Rt△ECF中,∵CE2+FC2=EF2,
∴x2+12=(3-x)2,解得x=,
∴EF=3-x=,∴cos∠EFC==.
8.C 【点拨】如图所示,在Rt△ABC中,∠C=90°,∠ABC=45°,延长CB使BD=AB,连接AD,得∠D=22.5°.
设AC=BC=1,则AB=BD=eq \r(2),
∴tan 22.5°===eq \r(2)-1.
9.C 【点拨】过A作AQ⊥BC于Q,过E作EM⊥BC于M,连接DE.
∵AB=AC,BC=8,tan∠ACB=y,
∴==y,CQ=4,
∴AQ=4y.
∵BE的垂直平分线交BC于D,BD=x,
∴BD=DE=x.
∵AQ⊥BC,EM⊥BC,∴AQ∥EM.
又∵E为AC的中点,
∴MC=CQ=2,∴EM=2y,DM=8-2-x=6-x.
在Rt△EDM中,由勾股定理得
x2=(2y)2+(6-x)2,即3x-y2=9.
10.C 【点拨】取BC的中点Q,连接EQ,FQ.
∵F为AB的中点,∴FQ=AC.
∵∠ACB=90°,∠A=30°,BC=6,
∴AC==eq \f(6, eq \f(,3))=6eq \r(3),∴FQ=3eq \r(3).
∵∠BEC=90°,Q为BC的中点,∴EQ=BC=3.
当E,F,Q三点共线时,EF的值最小,
∴EF=FQ-EQ=3eq \r(3)-3.
二、11.30 12.0.76
13.(25eq \r(3)-25) 【点拨】作PE⊥OB于点E,PF⊥CO于点F.
在Rt△AOC中,AO=100米,∠CAO=60°,
∴CO=AO·tan 60°=100eq \r(3)米.
设PE=x米,易知FO=x米.
∵=,∴AE=3x米.
在Rt△PCF中,∠CPF=45°,CF=(100eq \r(3)-x)米,
PF=OE=OA+AE=(100+3x)米.
∴PF=CF,∴100+3x=100eq \r(3)-x,
解得x=25eq \r(3)-25.∴PE=(25eq \r(3)-25)米.
14.(1)2 (2)222
【点拨】(1)当∠A+∠B=45°时,tan(∠A+∠B)==1,即tan A+tan B=1-tan Atan B,
∴(1+tan A)(1+tan B)=1+tan A+tan B+tan Atan B=1+1-tan Atan B+tan Atan B=2.
(2)由(1)可知(1+tan 1°)(1+tan 44°)=(1+tan 2°)(1+tan 43°)=…=2,∴原式=222.
三、15.【解】原式=×-2×+
=1-eq \r(3)+(tan 60°-1)
=1-eq \r(3)+eq \r(3)-1=0.
16.【解】(1)在Rt△ABD中,tan B==,AD=2,
∴BD=4,∴AB==2,
∴cos∠BAD==.
(2)∵sin C=,∴∠C=45°,
∴tan C==1,
∴CD=2,∴BC=BD+CD=6,
∴S△ABC=×AD·BC=6.
四、17.【解】(1)
(2)过点A作AE⊥BC于点E.
∵can B=,∴可设BC=8x,则AC=5x=AB.
易知BE=4x,
∴AE==3x.
∵S△ABC=24,
∴BC·AE=12x2=24,解得x=(负值已舍去),
故AB=AC=5eq \r(2),BC=8eq \r(2).
∴△ABC的周长=5eq \r(2)+5eq \r(2)+8eq \r(2)=18eq \r(2).
18.【解】∵∠AEB=90°,AB=200m,斜坡AB的坡度为 1:,
∴tan∠ABE===,∴∠ABE=30°,
∴AE=AB=100m.
∵AC=20m,∴CE=80m.
∵∠CED=90°,斜坡CD的坡度为1?4,
∴=,即=,
∴ED=320m.
∴CD==80(m).
∴斜坡CD的长是80m.
五、19.【解】(1) (2)∠ACB;(答案不唯一)
【点拨】利用网格构造直角三角形易得AB=,AC=2 ,BC=5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
∴sin∠ACB==.
(3)
20.【解】(1)∵AB=BC=13,AC=10,∠ABC的平分线与边AC交于点F,
∴∠ABF=∠FBC,BF⊥AC,AF=5.
在Rt△ABF中,BF==12.
∴sin A==.
(2)过点E作EG⊥BD,垂足为G.
∵CE平分∠ACD,EF⊥AC,EG⊥BD,
∴EF=EG.
在Rt△ABF中,sin∠ABF==.
在Rt△EBG中,sin∠EBG=sin∠ABF===,
BF=12,∴EG=.
∴点E到直线BD的距离是.
六、21.【解】设过A,B,C的水平线分别为AP,BM,CN,过A作AD⊥BM于D,交CN于E,则DE=10米,∠BAP=11.3°,∠PAC=14°,AP∥BM∥CN,
∴∠ABD=∠BAP=11.3°,∠ACE=∠PAC=14°.
设AE=x米,则AD=AE-DE=(x-10)米.
在Rt△ABD中,tan∠ABD==tan 11.3°≈0.20,
∴BD≈5AD=5(x-10)米.
在Rt△ACE中,tan∠ACE==tan 14°≈0.25,
∴CE≈4AE=4x米.
易知BD-CE=315米,
∴5(x-10)-4x≈315,
解得x≈365,即AE≈365米,
∴舰载机相对航母舰尾C的高度约为365米.
七、22.【解】(1)如图.由题意得∠BAD=45°,∠DAC=15°,∠FBC=60°,EF∥DA,
∴∠ABE=∠BAD=45°,
∴∠ABC=180°-∠ABE-∠FBC=75°.
∵∠BAC=∠BAD+∠DAC=60°,
∴∠C=180°-∠BAC-∠ABC=45°.
(2)如图,过点B作BG⊥AC,垂足为G.
在Rt△ABG中,AB=10千米,∠BAG=60°,
∴BG=AB·sin 60°=10×eq \f(,2)=5eq \r(3) (千米).
在Rt△BGC中,∠C=45°,
∴BC==eq \f(5eq \r(3),eq \f(,2))=5 (千米),
∴B,C两地间的距离为5eq \r(6)千米.
八、23.(1)【解】由面积公式可知S△ABC=bcsin A =bcsin 30°=
×2×3×=.
(2)【证明】∵S△ABC=S△ABD+S△BCD,
∴AB·BD·sin∠1+BC·BD·sin∠2=AB·BC·sin(∠1+∠2),
∴2BD·sin∠1+BD·sin∠2=2sin(∠1+∠2),
∴BD=.
(3)【证明】如图,作边长为1的等边三角形ABC,点D,E,F分别在AB,BC,AC上,且AD=a,BD=b,BE=c,EC=d,
CF=e,AF=f,则∠A=∠B=∠C=60°.
∵S△ADF+S△BDE+S△CEF<S△ABC,
∴af·sin 60°+bc·sin 60°+de·sin 60°
