人教版数学八年级下册 第十九章 一次函数测试卷(含解析)
文档属性
| 名称 | 人教版数学八年级下册 第十九章 一次函数测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 447.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 16:01:35 | ||
图片预览



文档简介
人教版数学八年级下册一次函数测试卷
一、选择题(共10题;共30分)
1.(3分) 下列各曲线中,不能表示y是x的函数是( )
A. B.
C. D.
2.(3分) 若函数是一次函数,则m值为( )
A. B.1 C. D.2
3.(3分) 已知一次函数表达式为:,则此一次函数图象不经过第( )象限.
A.一 B.二 C.三 D.四
4.(3分)关于正比例函数y=﹣3x,下列结论正确的是( )
A.图象不经过原点 B.y随x的增大而增大
C.图象经过第二、四象限 D.当x= 时,y=1
5.(3分)在函数(其中k、b为常数,且)的图象上有两个点,则下列各式中正确的是( )
A. B. C. D.
6.(3分)直线和的图象可能是( )
A. B.
C. D.
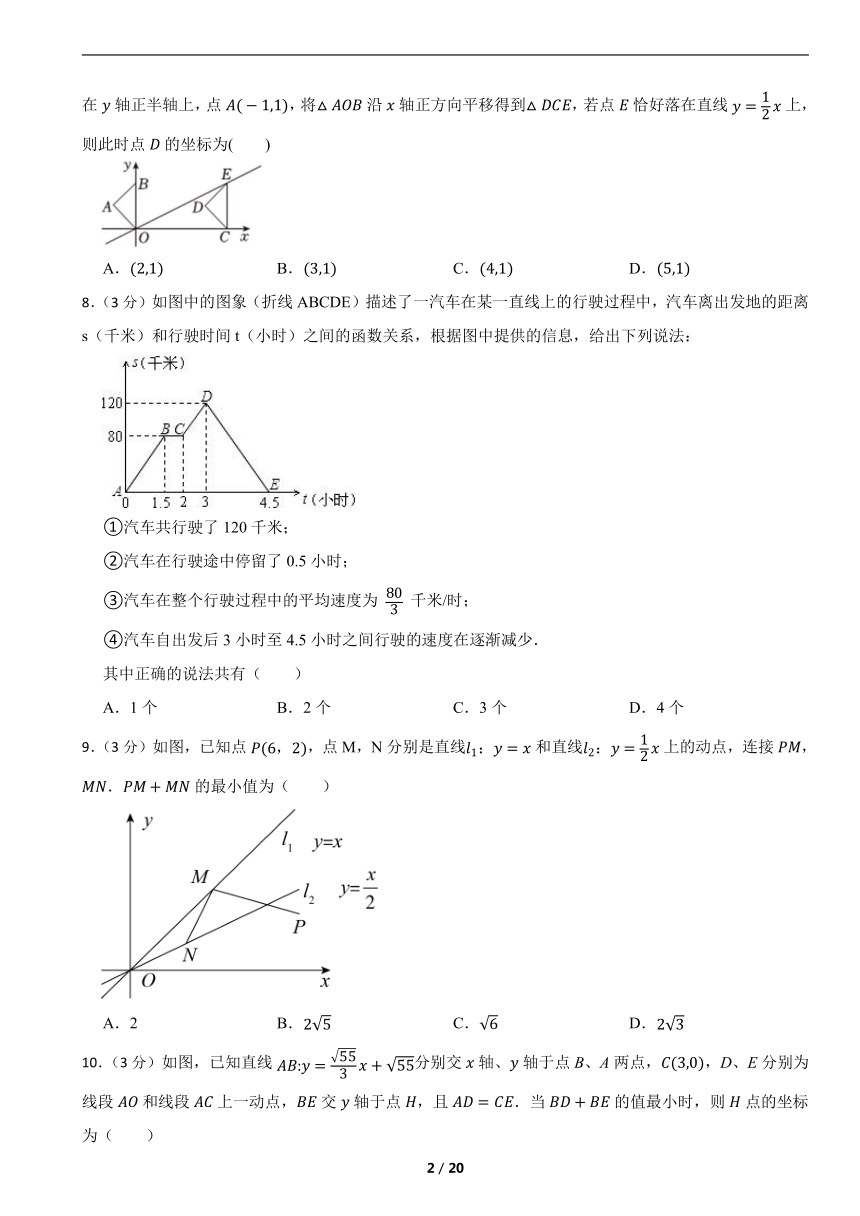
7.(3分)如图,在平面直角坐标系中,已知是以点为直角顶点的等腰直角三角形,点在轴正半轴上,点,将沿轴正方向平移得到,若点恰好落在直线上,则此时点的坐标为( )
A. B. C. D.
8.(3分)如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为 千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
9.(3分)如图,已知点,点M,N分别是直线和直线上的动点,连接,.的最小值为( )
A.2 B. C. D.
10.(3分)如图,已知直线分别交轴、轴于点B、A两点,,D、E分别为线段和线段上一动点,交轴于点,且.当的值最小时,则点的坐标为( )
A. B. C. D.
二、填空题(共6题;共30分)
11.(5分) 若将直线的图象先向左平移3个单位,再向下平移4个单位所得直线解析式是 .
12.(5分)如图,直线与相交于点,则关于的方程的解是 .
13.(5分) 已知一次函数的图象平行于直线,且经过点,则这个一次函数与坐标轴围成的图形面积为 .
14.(5分)已知一次函数的图象经过和,则关于x的不等式的解集为 .
15.(5分)约定:如果函数的图象经过点,我们就把此函数称作“族函数”,例如:正比例函数的图象经过点,所以正比例函数就是“族函数”.已知:一次函数和y=-x+1都是“族函数”,当时,一次函数的函数值y恰好有.则该一次函数的解析式为 .
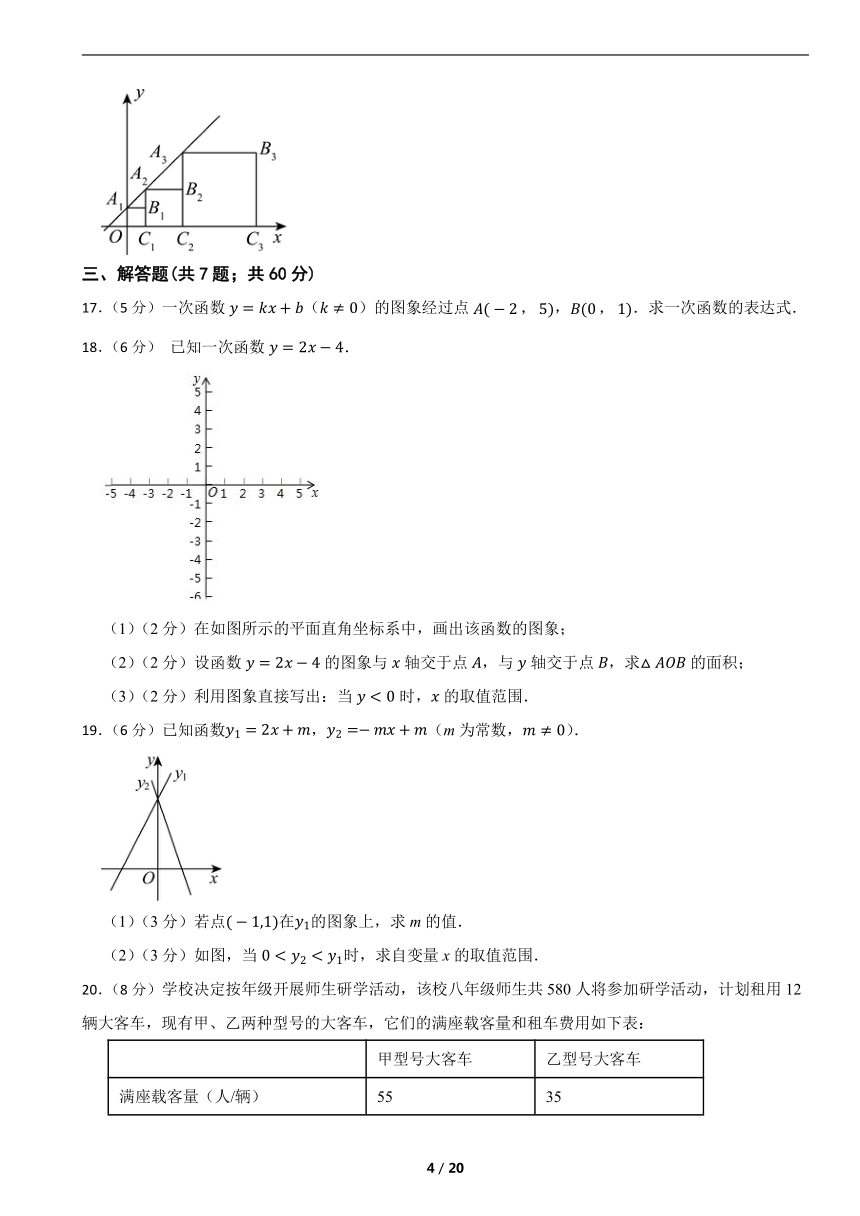
16.(5分)如图,正方形,,,…的顶点,,,…在直线上,顶点,,,…在x轴上,已知,,那么点的坐标为 .
三、解答题(共7题;共60分)
17.(5分)一次函数()的图象经过点,.求一次函数的表达式.
18.(6分) 已知一次函数.
(1)(2分)在如图所示的平面直角坐标系中,画出该函数的图象;
(2)(2分)设函数的图象与轴交于点,与轴交于点,求的面积;
(3)(2分)利用图象直接写出:当时,的取值范围.
19.(6分)已知函数,(m为常数,).
(1)(3分)若点在的图象上,求m的值.
(2)(3分)如图,当时,求自变量x的取值范围.
20.(8分)学校决定按年级开展师生研学活动,该校八年级师生共580人将参加研学活动,计划租用12辆大客车,现有甲、乙两种型号的大客车,它们的满座载客量和租车费用如下表:
甲型号大客车 乙型号大客车
满座载客量(人/辆) 55 35
租车费用(元/辆) 1200 800
(1)(3分)若租用的12辆大客车恰好能一次将八年级师生送到研学基地,求应分别租用甲、乙型号的大客车多少辆?
(2)(5分)设租用甲型号大客车x辆,租车总费用为y元.
①求出y(元)与x(辆)的函数关系式,并求出x的取值范围;
②当租用甲型号大客车多少辆时,租车的总费用最少,最少费用是多少?
21.(10分)如图,正方形AOBC的边长为2,点O为坐标原点,边OB,OA分别在x轴,y轴上,点D是BC的中点,点P是线段AC上的一个点,如果将OA沿直线OP对折,使点A的对应点A'恰好落在PD所在的直线上.
(1)(2分)连接OD,求证:△A'OD≌△BOD;
(2)(3分)利用你所学的数学知识求出折痕OP所在直线的函解式;
(3)(5分)请问x轴上是否存在一点,使△DPQ的周长有最小值?若存在,请求出点Q的坐标;若不存在,请说明理由.
22.(10分)【学习材料】
求直线向右平移个单位长度后的解析式. 第一步,在直线上任意取两点和; 第二步,将点和向右平移个单位长度得到点和,则直线就是直线向右平移个单位长度后得到的直线; 第三步,设直线的解析式为:,将和代入得到:解得,所以直线的解析式为:.
(1)(4分)【类比思考】
若将直线向左平移个单位长度,则平移后的直线解析式为 ;
若先将直线向右平移个单位长度,再向下平移个单位长度,得到直线,则直线的解析式为 .
(2)(6分)【拓展应用】
已知一次函数的图象与直线关于轴对称,求一次函数的解析式;
若一次函数的图象绕点逆时针旋转后得到直线,则直线的解析式为 ▲ .
23.(15分) 如图,平面直角坐标系xOy中,正方形ABCD的边AB在x轴上,点O是AB的中点,直线l:y=kx+2k+4过定点D,交x轴于点P.
(1)(4分)求正方形ABCD的边长;
(2)(5分)如图1,在直线l上有一点N,,连接BN,点M为BN中点,连接AM,求线段AM的长度的最小值,并求出此时点N的坐标.
(3)(6分)如图2,过点P作PE⊥DP交∠CBx的平分线于点E,点Q是直线AD上一点,四边形PQCE是否可能为菱形,如果能求出此时直线CQ的解析式,如果不能,则说明理由.
答案解析部分
1.【答案】C
2.【答案】C
【解析】【解答】 函数是一次函数,
且
解得m=-1,
故答案为:C.
【分析】根据一次函数的定义得到且解得m的值,从而求解.
3.【答案】B
【解析】【解答】 一次函数表达式为:,则此一次函数图象不经过第二象限.
故答案为:B.
【分析】根据一次函数的图象所经过的象限即可求解.
4.【答案】C
【解析】【解答】解:A、显然当x=0时,y=0,故图象经过原点,不符合题意;
B、k<0,应y随x的增大而减小,不符合题意;
C、k<0,图解经过二、四象限,符合题意;
D、把x= 代入,得:y=-1,不符合题意.
故答案为:C.
【分析】利用正比例函数的性质和图形逐项判定即可。
5.【答案】A
【解析】【解答】解:∵函数(其中k、b为常数,且),
∴y随x的增大而减小,
又∵点,是函数上的两点,
,
∴.
故答案为:A.
【分析】利用一次函数的性质求解即可。
6.【答案】C
【解析】【解答】解:
的图像与y轴的交点坐标在x轴上方,故排除A、B选项
C、如果过第一、二、四象限的图象是y1,由y1的图象可知,m<0;由y2的图象可知,m<0,两结论不互相矛盾,故符合题意;
D、如果过第一、二、三象限的图象是y1,由y1的图象可知,m>0;由y2的图象可知,m <0,两结论相矛盾,故不符合题意.
故答案为:C.
【分析】根据函数解析式的图象与性质对每个选项一一判断即可。
7.【答案】B
【解析】【解答】解:点A的坐标为(-1,1),
∴
∵△OAB是以点A为直角顶点的等腰直角三角形,
∴
∴点B的坐标为(0,2),
∵点E是点B向右平移得到的点,
∴点E的纵坐标为2,
当y=2时,
解得x=4,
∴点E的坐标为(4,2);
∴点E是点B向右平移4个单位长度得到的点,
∴点D是点A向右平移4个单位长度得到的,
∴点D的坐标为(3,1).
故答案为:B.
【分析】由点A的坐标,可得出OA的长,结合等腰直角三角形的性质,可得出AB的长,由平移的性质,可知点E的纵坐标为2,利用一次函数图象上点的坐标特征,可得出点E的坐标,结合点B的坐标,可得出点E是点B向右平移4个单位长度得到的点,进而可得出点D是点A向右平移4个单位长度得到的点,再结合点A的坐标,即可得出点D的坐标.
8.【答案】A
【解析】【解答】解:由图象可知,汽车走到距离出发点120千米的地方后又返回出发点,所以汽车共行驶了240千米,①错;
从1.5时开始到2时结束,时间在增多,而路程没有变化,说明此时在停留,停留了2﹣1.5=0.5小时,②对;
汽车用4.5小时走了240千米,平均速度为:240÷4.5= 千米/时,③错.
汽车自出发后3小时至4.5小时,图象是直线形式,说明是在匀速前进,④错.
故选A.
【分析】根据图象上的特殊点的实际意义即可作出判断.
9.【答案】B
【解析】【解答】解:作点P关于直线l1:y=x的对称点P′,如图,过点P′作y轴的垂线,与直线l1:y=x交于点B,
在正方形OABC 中,OC=CB=BA=AO=6,
∵直线l1:y=x经过点O(0,0),B(6,6),
∴直线l1:y=x是正方形OABC的对称轴,
∵点P(6,2)在BC上,
∴可得点P关于l1:y=x的对称点P′(2,6),
当x=6时,,
即直线l2:经过点H(6,3),
过点P′(2,6)作P′N垂直直线l2:于点N,即P′N⊥OH于点N,交直线l1:y=x于点M,
∵P(6,2)和P′(2,6)关于l1:y=x对称,
∴PM=P′M,
∴PM+MN=P′M+MN=P′N,即PM+MN的最小值为P′N的长,
∴OH=
∵,
S△POH=S正方形OABC-S△POA-S△PBH-S△COH=6×6-
解得
即PM+MN的最小值
故答案为:B.
【分析】在坐标系中构造边长为6的正方形OABC,可得得点P关于l1的对称点P′的坐标,连接P′M,P′N,可说明PM+MN≥P′N,当P′,M,N三点在同一直线上时,PM+MN=P′N,也就是此时PM+MN的最小值为P′N,根据点到直线,垂线段最短,过点P′(2,6)作P′N垂直直线l2于点N,即P′N⊥OH于点N,交直线l1于点M,此时P′N最小,利用△POH的面积的不同算法,列出关于P′N方程求解.
10.【答案】A
【解析】【解答】解:由题意,,,,
取点,连接.
,,,
,,,,
,,,
,,
,的最小值为线段的长,
当B,E,F共线时,的值最小,
直线的解析式为:,,
当的值最小时,则H点的坐标为(0,4),
故选:A.
【分析】首先证明AB=AC=8,取点 F (3,8),连接CF,EF,BF.由△ECF=△DAB(SAS),推出BD=EF ,推出BD+BE=BE+EF,因为BE+EF≥BF ,推出BD+BE的最小值为线段BF的长,推出当B,E , F共线时,BD+BE的值最小,求出直线BF的解析式即可解决问题.
11.【答案】
【解析】【解答】解:由题意,得
故答案为:.
【分析】一次函数图象的平移规律:左加右减,上加下减,据此求解。
12.【答案】
【解析】【解答】解:∵直线与相交于点,
∴关于的方程的解是
故答案为:.
【分析】根据函数图象,交点的横坐标即为方程的解.
13.【答案】16
【解析】【解答】解:∵一次函数的图象平行于直线,
∴,
∴把点代入得,,
解得,
∴,;
∴一次函数的解析式为.
∵时,;时,,
∴函数与x轴、y轴的交点分别为和,
∴所围成的三角形的面积.
故答案为;16.
【分析】根据两平行直线的解析式的k值相等求出k,把点P的坐标代入解析式求出b值,求得函数的解析式,利用解根式求直线与x轴、y轴的交点坐标,根据三角形的面积公式求解即可。
14.【答案】
【解析】【解答】将点(4,0)和(0,-3)分别代入,
可得:,
解得:,
∴一次函数解析式为:,
∴,即,
解得:,
故答案为:.
【分析】先将点(4,0)和(0,-3)代入解析式求出k、b的值,再利用一元一次不等式的解法求解即可.
15.【答案】或
【解析】【解答】解:∵一次函数和y=-x+1都是“族函数”,
∴一次函数和y=-x+1都经过 ,
∴
解得:,
∴当时,一次函数的函数值y恰好有,
①当时,y随x增大而增大,
∴一次函数经过,
解得:,
∴解析式为:,
②当时,y随x增大而减小,
一次函数经过,
解得:,
∴解析式为:,
综上所述:该一次函数的解析式为:或.
故答案为:或.
【分析】根据族函数的定义得到:当时,一次函数的函数值y恰好有,再分情况讨论:①:当时,②当时,根据一次函数的增减性结合待定系数法即可求出一次函数的解析式.
16.【答案】
【解析】【解答】解:∵A1(0,1),A2(1,2),
∴直线y=kx+b(k≠0)为y=x+1,
由题意可推断出:点B1(1,1),B2(3,2),
∴Bn的横坐标为An+1的横坐标,纵坐标为An的纵坐标,
又∵An的横坐标数列为An=2n-1-1,
∴纵坐标为2n-1,
∴Bn的坐标为[A(n+1)的横坐标,An的纵坐标]=(2n-1,2n-1),
∴B2023(22023-1,22022),
故答案为:(22023-1,22022).
【分析】本题将平面直角坐标系与一次函数解析式相结合考查找规律问题,根据一次函数经过的点确定一次函数解析式,再通过解析式确认Bn的坐标为[A(n+1)的横坐标,An的纵坐标]=(2n-1,2n-1),即可求解.
17.【答案】解:∵直线过点,.
∴
∴
∴一次函数的表达式为.
【解析】【分析】考查的是待定系数法求一次函数解析式。
18.【答案】(1)解:列表如下:
描点并连线如下:
.
(2)解:由(1)得:,,
∴;
(3)解:由图象可得:
当时,.
【解析】【分析】(1)根据列表、描点、连线即可求解;
(2)先求出OA,OB的值,再利用三角形的面积公式即可求解;
(3)通过观察图象即可求解.
19.【答案】(1)解:把代入,得到,
∴
(2)解:联立,解得,
∴两条直线的交点的横坐标为,
∵,
∴当时:,解得:,
由图可知:当时,.
【解析】【分析】(1)把代入,即可求出m的值;
(2)联立,解得,即两条直线的交点的横坐标为,然后求出y2和x轴的交点,进而即可求解.
20.【答案】(1)解:设租用甲型号的大客车x辆,则租用甲型号的大客车辆,
依题意得,
解得,
,
答:租用甲型号的大客车8辆,租用甲型号的大客车4辆
(2)解:①设租用甲型号的大客车x辆,则租用甲型号的大客车辆,
依题意得,
,解得,
∴;
②∵,
∴当时,y有最小值,最小值为12800,
,
答:租用甲型号的大客车8辆,租用甲型号的大客车4辆时,费用最少,为12800元.
【解析】【分析】(1) 设租用甲型号的大客车x辆,则租用甲型号的大客车(12-x)辆,根据相等关系:甲型客车装载人数+乙型客车装载人数=580,可得方程:得解方程,即可求得两种型号客车的辆数;
(2)①①设租用甲型号的大客车x辆,则租用甲型号的大客车(12-x)辆,根据总费用=租甲型客车费用+租乙型客车费用,可得关系式为:并根据客车总辆数为12,得x≤12,根据师生人数为580人,可得不等关系为:联合成不等式组,解不等式组即可求出自变量的取值范围;②由①知:y=400x+9600(8≤x≤12),根据一次函数的性质知,ysuix的增大而增大,所以当x取最小值时,总费用y最小,所以只需求出当x取最小值8时所对应的函数值即可。
21.【答案】(1)证明:∵四边形OACB是正方形,
∴∠OAP=∠OBC=90°,OA=OB,
由轴对称的性质可知OA=OA',∠OA'P='OAP=90°,
∴OA'=OB,∠OA'D=∠OBD=90°,
∵OD=OD,
∴Rt△A'OD≌Rt△BOD(HL);
(2)解:连接OD,
∵正方形AOBC的边长为2,点D是BC的中点,
∴.
由折叠的性质可知,OA'=OA=2,∠OA'D=90°.
∴A'D=1.
设点P(x,2),PA'=x,PC=2﹣x,CD=1.
∴(x+1)2=(2﹣x)2+12.
解得x=.
所以P(,2),
∴OP所在直线的表达式是y=3x;
(3)解:存在.若△DPQ的周长为最小,
即是要PQ+DQ为最小.
∵点D关于x轴的对称点是D'(2,﹣1),
∴设直线PD'的解析式为y=kx+b,
,
解得,
∴直线PD'的函数表达式为.
当y=0时,x=.
∴点Q(,0).
22.【答案】(1);
(2)解:①设直线上的点的坐标为,它们对应的关于轴对称点的坐标为,
直线关于轴对称的直线为,即;②
【解析】【解答】解:(1)【类比思考】
根据【学习材料】中的方法:
第一步,在直线上任意取两点和;
第二步,将点和向左平移个单位长度,得到点和,则直线就是直线向左平移个单位长度后得到的直线;
第三步,设直线的解析式为:,将和代入,
得到,解得.
直线的解析式为.
故答案为:.
根据【学习材料】中的方法:
第一步,在直线上任意取两点和;
第二步,将点和向右平移个单位长度,得到点和;再将点和向下平移个单位长度,得到点和,则直线就是所要求的直线.
第三步,设直线的解析式为,将和代入,
得到,解得.
直线的解析式为.
故答案为:.
(2)【拓展应用】设直线的解析式为.
的图象绕点逆时针旋转后得到直线,
点在直线上.
将代入,
得.
当时,,
与轴交点坐标为.
由几何关系,利用勾股定理,
得,解得.
.
.
故答案为:.
【分析】【类比思考】题目根据题意,按照【学习材料】中给定的解题方法求解即可;
【拓展应用】已知一次函数的图象与直线关于x轴对称,则直线上的点关于x轴对称的点的坐标为(x,-y),代入整理求解即可;
设直线m的解析式为y=ax+c,点(3,0)和(0,c)在直线m上,将(3,0)代入y=ax+c,利用勾股定理求解c,将a、c的值代回y=ax+c求解即可.
23.【答案】(1)解:由y=kx+2k+4,得y﹣4=k(x+2),
∵直线l:y=kx+2k+4过定点D,
∴x与y的值与k无关,
∴,
解得,
∴D(﹣2,4),
∴正方形ABCD的边长为4
(2)解:如图,连接BD,取BD中点E,连EM,EA,
∵在正方形ABCD中,正方形ABCD的边长为4,
∴AB=AD=4,∠DAB=90°,
∴BD= ,DN=AB=2,
∵点M、E分别为BN、BD的中点,
∴EM=DN=1,
∵∠DAB=90°,点E为BD的中点,
∴AE=BD=,
当点A、M、E三点不共线时,
在AME中,AM>AE-ME=-1,
当点A、M、E三点共线时,AM=AE-ME=-1,
∴AM≥-1,
∴当点A、M、E三点共线时,AM有最小值为-1;
此时,如下图,过点N作NF⊥x轴于点F,则NF∥AD,
设N(x,y),
∴
∴
∴
解得NF=PF=4﹣,
∴OF=OA+AP﹣PF
=2+4﹣(4﹣)
=2+
∴此时N(﹣2﹣,4﹣).
(3)解:如图,当点Q与点D重合,点P与点A重合,点E与点B重合,
此时四边形PQCE为正方形ADCB,符合题意,
此时直线CQ的解析式为:y=4;
如图,当点Q在x轴下方时,
∵四边形PQCE为菱形,
∴QP=QC=CE=EP,CQ∥PE,
∵PE⊥DP,
∴CQ⊥DP,
∴∠1+∠3=90°,
∵∠ADC=90°,
∴∠1+∠2=90°,
∴∠2=∠3,
又∵∠CDA=∠DAB=90°,CD=AD,
∴CDQ≌DAP(AAS),
∴CQ=DP,
又∵PQ=CQ,
∴PQ=PD,
∵PA⊥DQ,
∴AQ=AD=4,
∴点Q(-2,-4),
又∵C(2,4),
∴设直线CQ为y=kx+b,
则
解得
∴直线CQ:y=2x.
综上所述,四边形PQCE可以为菱形,此时直线CQ的解析式为y=4或y=2x.
【解析】【分析】(1)由y=kx+2k+4变形得y﹣4=k(x+2),根据直线过定点D,可知 x与y的值与k无关,得到 ,解方程组得到点D的坐标,即可得出正方形的边长;
(2)连接BD,取BD中点E,连EM,EA, 先根据正方形的性质及勾股定理求出DN的长,再根据三角形中位线定理可得EM=1,再根据三角形的两边之和大于第三边得出 AM>AE-ME ,进而可得当点A、M、E三点共线时,AM有最小值-1;过点N作NF⊥x轴于点F,则NF∥AD,设N(x,y),由建立方程求出 F=PF=4﹣, 进而得出OF的长,据此可得点N的坐标;
(3) 分两种情况讨论,当点Q与点D重合,点P与点A重合,点E与点B重合, 符合题意, 结合正方形的边长可知直线CQ的解析式为y=4; 当点Q在x轴下方时, 先证CDQ≌DAP,根据全等三角形的性质得到 CQ=DP, 进而得到点Q的坐标为(-2,-4),再结合点C的坐标,利用待定系数法求 直线CQ的解析式即可.
1 / 1
一、选择题(共10题;共30分)
1.(3分) 下列各曲线中,不能表示y是x的函数是( )
A. B.
C. D.
2.(3分) 若函数是一次函数,则m值为( )
A. B.1 C. D.2
3.(3分) 已知一次函数表达式为:,则此一次函数图象不经过第( )象限.
A.一 B.二 C.三 D.四
4.(3分)关于正比例函数y=﹣3x,下列结论正确的是( )
A.图象不经过原点 B.y随x的增大而增大
C.图象经过第二、四象限 D.当x= 时,y=1
5.(3分)在函数(其中k、b为常数,且)的图象上有两个点,则下列各式中正确的是( )
A. B. C. D.
6.(3分)直线和的图象可能是( )
A. B.
C. D.
7.(3分)如图,在平面直角坐标系中,已知是以点为直角顶点的等腰直角三角形,点在轴正半轴上,点,将沿轴正方向平移得到,若点恰好落在直线上,则此时点的坐标为( )
A. B. C. D.
8.(3分)如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为 千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
9.(3分)如图,已知点,点M,N分别是直线和直线上的动点,连接,.的最小值为( )
A.2 B. C. D.
10.(3分)如图,已知直线分别交轴、轴于点B、A两点,,D、E分别为线段和线段上一动点,交轴于点,且.当的值最小时,则点的坐标为( )
A. B. C. D.
二、填空题(共6题;共30分)
11.(5分) 若将直线的图象先向左平移3个单位,再向下平移4个单位所得直线解析式是 .
12.(5分)如图,直线与相交于点,则关于的方程的解是 .
13.(5分) 已知一次函数的图象平行于直线,且经过点,则这个一次函数与坐标轴围成的图形面积为 .
14.(5分)已知一次函数的图象经过和,则关于x的不等式的解集为 .
15.(5分)约定:如果函数的图象经过点,我们就把此函数称作“族函数”,例如:正比例函数的图象经过点,所以正比例函数就是“族函数”.已知:一次函数和y=-x+1都是“族函数”,当时,一次函数的函数值y恰好有.则该一次函数的解析式为 .
16.(5分)如图,正方形,,,…的顶点,,,…在直线上,顶点,,,…在x轴上,已知,,那么点的坐标为 .
三、解答题(共7题;共60分)
17.(5分)一次函数()的图象经过点,.求一次函数的表达式.
18.(6分) 已知一次函数.
(1)(2分)在如图所示的平面直角坐标系中,画出该函数的图象;
(2)(2分)设函数的图象与轴交于点,与轴交于点,求的面积;
(3)(2分)利用图象直接写出:当时,的取值范围.
19.(6分)已知函数,(m为常数,).
(1)(3分)若点在的图象上,求m的值.
(2)(3分)如图,当时,求自变量x的取值范围.
20.(8分)学校决定按年级开展师生研学活动,该校八年级师生共580人将参加研学活动,计划租用12辆大客车,现有甲、乙两种型号的大客车,它们的满座载客量和租车费用如下表:
甲型号大客车 乙型号大客车
满座载客量(人/辆) 55 35
租车费用(元/辆) 1200 800
(1)(3分)若租用的12辆大客车恰好能一次将八年级师生送到研学基地,求应分别租用甲、乙型号的大客车多少辆?
(2)(5分)设租用甲型号大客车x辆,租车总费用为y元.
①求出y(元)与x(辆)的函数关系式,并求出x的取值范围;
②当租用甲型号大客车多少辆时,租车的总费用最少,最少费用是多少?
21.(10分)如图,正方形AOBC的边长为2,点O为坐标原点,边OB,OA分别在x轴,y轴上,点D是BC的中点,点P是线段AC上的一个点,如果将OA沿直线OP对折,使点A的对应点A'恰好落在PD所在的直线上.
(1)(2分)连接OD,求证:△A'OD≌△BOD;
(2)(3分)利用你所学的数学知识求出折痕OP所在直线的函解式;
(3)(5分)请问x轴上是否存在一点,使△DPQ的周长有最小值?若存在,请求出点Q的坐标;若不存在,请说明理由.
22.(10分)【学习材料】
求直线向右平移个单位长度后的解析式. 第一步,在直线上任意取两点和; 第二步,将点和向右平移个单位长度得到点和,则直线就是直线向右平移个单位长度后得到的直线; 第三步,设直线的解析式为:,将和代入得到:解得,所以直线的解析式为:.
(1)(4分)【类比思考】
若将直线向左平移个单位长度,则平移后的直线解析式为 ;
若先将直线向右平移个单位长度,再向下平移个单位长度,得到直线,则直线的解析式为 .
(2)(6分)【拓展应用】
已知一次函数的图象与直线关于轴对称,求一次函数的解析式;
若一次函数的图象绕点逆时针旋转后得到直线,则直线的解析式为 ▲ .
23.(15分) 如图,平面直角坐标系xOy中,正方形ABCD的边AB在x轴上,点O是AB的中点,直线l:y=kx+2k+4过定点D,交x轴于点P.
(1)(4分)求正方形ABCD的边长;
(2)(5分)如图1,在直线l上有一点N,,连接BN,点M为BN中点,连接AM,求线段AM的长度的最小值,并求出此时点N的坐标.
(3)(6分)如图2,过点P作PE⊥DP交∠CBx的平分线于点E,点Q是直线AD上一点,四边形PQCE是否可能为菱形,如果能求出此时直线CQ的解析式,如果不能,则说明理由.
答案解析部分
1.【答案】C
2.【答案】C
【解析】【解答】 函数是一次函数,
且
解得m=-1,
故答案为:C.
【分析】根据一次函数的定义得到且解得m的值,从而求解.
3.【答案】B
【解析】【解答】 一次函数表达式为:,则此一次函数图象不经过第二象限.
故答案为:B.
【分析】根据一次函数的图象所经过的象限即可求解.
4.【答案】C
【解析】【解答】解:A、显然当x=0时,y=0,故图象经过原点,不符合题意;
B、k<0,应y随x的增大而减小,不符合题意;
C、k<0,图解经过二、四象限,符合题意;
D、把x= 代入,得:y=-1,不符合题意.
故答案为:C.
【分析】利用正比例函数的性质和图形逐项判定即可。
5.【答案】A
【解析】【解答】解:∵函数(其中k、b为常数,且),
∴y随x的增大而减小,
又∵点,是函数上的两点,
,
∴.
故答案为:A.
【分析】利用一次函数的性质求解即可。
6.【答案】C
【解析】【解答】解:
的图像与y轴的交点坐标在x轴上方,故排除A、B选项
C、如果过第一、二、四象限的图象是y1,由y1的图象可知,m<0;由y2的图象可知,m<0,两结论不互相矛盾,故符合题意;
D、如果过第一、二、三象限的图象是y1,由y1的图象可知,m>0;由y2的图象可知,m <0,两结论相矛盾,故不符合题意.
故答案为:C.
【分析】根据函数解析式的图象与性质对每个选项一一判断即可。
7.【答案】B
【解析】【解答】解:点A的坐标为(-1,1),
∴
∵△OAB是以点A为直角顶点的等腰直角三角形,
∴
∴点B的坐标为(0,2),
∵点E是点B向右平移得到的点,
∴点E的纵坐标为2,
当y=2时,
解得x=4,
∴点E的坐标为(4,2);
∴点E是点B向右平移4个单位长度得到的点,
∴点D是点A向右平移4个单位长度得到的,
∴点D的坐标为(3,1).
故答案为:B.
【分析】由点A的坐标,可得出OA的长,结合等腰直角三角形的性质,可得出AB的长,由平移的性质,可知点E的纵坐标为2,利用一次函数图象上点的坐标特征,可得出点E的坐标,结合点B的坐标,可得出点E是点B向右平移4个单位长度得到的点,进而可得出点D是点A向右平移4个单位长度得到的点,再结合点A的坐标,即可得出点D的坐标.
8.【答案】A
【解析】【解答】解:由图象可知,汽车走到距离出发点120千米的地方后又返回出发点,所以汽车共行驶了240千米,①错;
从1.5时开始到2时结束,时间在增多,而路程没有变化,说明此时在停留,停留了2﹣1.5=0.5小时,②对;
汽车用4.5小时走了240千米,平均速度为:240÷4.5= 千米/时,③错.
汽车自出发后3小时至4.5小时,图象是直线形式,说明是在匀速前进,④错.
故选A.
【分析】根据图象上的特殊点的实际意义即可作出判断.
9.【答案】B
【解析】【解答】解:作点P关于直线l1:y=x的对称点P′,如图,过点P′作y轴的垂线,与直线l1:y=x交于点B,
在正方形OABC 中,OC=CB=BA=AO=6,
∵直线l1:y=x经过点O(0,0),B(6,6),
∴直线l1:y=x是正方形OABC的对称轴,
∵点P(6,2)在BC上,
∴可得点P关于l1:y=x的对称点P′(2,6),
当x=6时,,
即直线l2:经过点H(6,3),
过点P′(2,6)作P′N垂直直线l2:于点N,即P′N⊥OH于点N,交直线l1:y=x于点M,
∵P(6,2)和P′(2,6)关于l1:y=x对称,
∴PM=P′M,
∴PM+MN=P′M+MN=P′N,即PM+MN的最小值为P′N的长,
∴OH=
∵,
S△POH=S正方形OABC-S△POA-S△PBH-S△COH=6×6-
解得
即PM+MN的最小值
故答案为:B.
【分析】在坐标系中构造边长为6的正方形OABC,可得得点P关于l1的对称点P′的坐标,连接P′M,P′N,可说明PM+MN≥P′N,当P′,M,N三点在同一直线上时,PM+MN=P′N,也就是此时PM+MN的最小值为P′N,根据点到直线,垂线段最短,过点P′(2,6)作P′N垂直直线l2于点N,即P′N⊥OH于点N,交直线l1于点M,此时P′N最小,利用△POH的面积的不同算法,列出关于P′N方程求解.
10.【答案】A
【解析】【解答】解:由题意,,,,
取点,连接.
,,,
,,,,
,,,
,,
,的最小值为线段的长,
当B,E,F共线时,的值最小,
直线的解析式为:,,
当的值最小时,则H点的坐标为(0,4),
故选:A.
【分析】首先证明AB=AC=8,取点 F (3,8),连接CF,EF,BF.由△ECF=△DAB(SAS),推出BD=EF ,推出BD+BE=BE+EF,因为BE+EF≥BF ,推出BD+BE的最小值为线段BF的长,推出当B,E , F共线时,BD+BE的值最小,求出直线BF的解析式即可解决问题.
11.【答案】
【解析】【解答】解:由题意,得
故答案为:.
【分析】一次函数图象的平移规律:左加右减,上加下减,据此求解。
12.【答案】
【解析】【解答】解:∵直线与相交于点,
∴关于的方程的解是
故答案为:.
【分析】根据函数图象,交点的横坐标即为方程的解.
13.【答案】16
【解析】【解答】解:∵一次函数的图象平行于直线,
∴,
∴把点代入得,,
解得,
∴,;
∴一次函数的解析式为.
∵时,;时,,
∴函数与x轴、y轴的交点分别为和,
∴所围成的三角形的面积.
故答案为;16.
【分析】根据两平行直线的解析式的k值相等求出k,把点P的坐标代入解析式求出b值,求得函数的解析式,利用解根式求直线与x轴、y轴的交点坐标,根据三角形的面积公式求解即可。
14.【答案】
【解析】【解答】将点(4,0)和(0,-3)分别代入,
可得:,
解得:,
∴一次函数解析式为:,
∴,即,
解得:,
故答案为:.
【分析】先将点(4,0)和(0,-3)代入解析式求出k、b的值,再利用一元一次不等式的解法求解即可.
15.【答案】或
【解析】【解答】解:∵一次函数和y=-x+1都是“族函数”,
∴一次函数和y=-x+1都经过 ,
∴
解得:,
∴当时,一次函数的函数值y恰好有,
①当时,y随x增大而增大,
∴一次函数经过,
解得:,
∴解析式为:,
②当时,y随x增大而减小,
一次函数经过,
解得:,
∴解析式为:,
综上所述:该一次函数的解析式为:或.
故答案为:或.
【分析】根据族函数的定义得到:当时,一次函数的函数值y恰好有,再分情况讨论:①:当时,②当时,根据一次函数的增减性结合待定系数法即可求出一次函数的解析式.
16.【答案】
【解析】【解答】解:∵A1(0,1),A2(1,2),
∴直线y=kx+b(k≠0)为y=x+1,
由题意可推断出:点B1(1,1),B2(3,2),
∴Bn的横坐标为An+1的横坐标,纵坐标为An的纵坐标,
又∵An的横坐标数列为An=2n-1-1,
∴纵坐标为2n-1,
∴Bn的坐标为[A(n+1)的横坐标,An的纵坐标]=(2n-1,2n-1),
∴B2023(22023-1,22022),
故答案为:(22023-1,22022).
【分析】本题将平面直角坐标系与一次函数解析式相结合考查找规律问题,根据一次函数经过的点确定一次函数解析式,再通过解析式确认Bn的坐标为[A(n+1)的横坐标,An的纵坐标]=(2n-1,2n-1),即可求解.
17.【答案】解:∵直线过点,.
∴
∴
∴一次函数的表达式为.
【解析】【分析】考查的是待定系数法求一次函数解析式。
18.【答案】(1)解:列表如下:
描点并连线如下:
.
(2)解:由(1)得:,,
∴;
(3)解:由图象可得:
当时,.
【解析】【分析】(1)根据列表、描点、连线即可求解;
(2)先求出OA,OB的值,再利用三角形的面积公式即可求解;
(3)通过观察图象即可求解.
19.【答案】(1)解:把代入,得到,
∴
(2)解:联立,解得,
∴两条直线的交点的横坐标为,
∵,
∴当时:,解得:,
由图可知:当时,.
【解析】【分析】(1)把代入,即可求出m的值;
(2)联立,解得,即两条直线的交点的横坐标为,然后求出y2和x轴的交点,进而即可求解.
20.【答案】(1)解:设租用甲型号的大客车x辆,则租用甲型号的大客车辆,
依题意得,
解得,
,
答:租用甲型号的大客车8辆,租用甲型号的大客车4辆
(2)解:①设租用甲型号的大客车x辆,则租用甲型号的大客车辆,
依题意得,
,解得,
∴;
②∵,
∴当时,y有最小值,最小值为12800,
,
答:租用甲型号的大客车8辆,租用甲型号的大客车4辆时,费用最少,为12800元.
【解析】【分析】(1) 设租用甲型号的大客车x辆,则租用甲型号的大客车(12-x)辆,根据相等关系:甲型客车装载人数+乙型客车装载人数=580,可得方程:得解方程,即可求得两种型号客车的辆数;
(2)①①设租用甲型号的大客车x辆,则租用甲型号的大客车(12-x)辆,根据总费用=租甲型客车费用+租乙型客车费用,可得关系式为:并根据客车总辆数为12,得x≤12,根据师生人数为580人,可得不等关系为:联合成不等式组,解不等式组即可求出自变量的取值范围;②由①知:y=400x+9600(8≤x≤12),根据一次函数的性质知,ysuix的增大而增大,所以当x取最小值时,总费用y最小,所以只需求出当x取最小值8时所对应的函数值即可。
21.【答案】(1)证明:∵四边形OACB是正方形,
∴∠OAP=∠OBC=90°,OA=OB,
由轴对称的性质可知OA=OA',∠OA'P='OAP=90°,
∴OA'=OB,∠OA'D=∠OBD=90°,
∵OD=OD,
∴Rt△A'OD≌Rt△BOD(HL);
(2)解:连接OD,
∵正方形AOBC的边长为2,点D是BC的中点,
∴.
由折叠的性质可知,OA'=OA=2,∠OA'D=90°.
∴A'D=1.
设点P(x,2),PA'=x,PC=2﹣x,CD=1.
∴(x+1)2=(2﹣x)2+12.
解得x=.
所以P(,2),
∴OP所在直线的表达式是y=3x;
(3)解:存在.若△DPQ的周长为最小,
即是要PQ+DQ为最小.
∵点D关于x轴的对称点是D'(2,﹣1),
∴设直线PD'的解析式为y=kx+b,
,
解得,
∴直线PD'的函数表达式为.
当y=0时,x=.
∴点Q(,0).
22.【答案】(1);
(2)解:①设直线上的点的坐标为,它们对应的关于轴对称点的坐标为,
直线关于轴对称的直线为,即;②
【解析】【解答】解:(1)【类比思考】
根据【学习材料】中的方法:
第一步,在直线上任意取两点和;
第二步,将点和向左平移个单位长度,得到点和,则直线就是直线向左平移个单位长度后得到的直线;
第三步,设直线的解析式为:,将和代入,
得到,解得.
直线的解析式为.
故答案为:.
根据【学习材料】中的方法:
第一步,在直线上任意取两点和;
第二步,将点和向右平移个单位长度,得到点和;再将点和向下平移个单位长度,得到点和,则直线就是所要求的直线.
第三步,设直线的解析式为,将和代入,
得到,解得.
直线的解析式为.
故答案为:.
(2)【拓展应用】设直线的解析式为.
的图象绕点逆时针旋转后得到直线,
点在直线上.
将代入,
得.
当时,,
与轴交点坐标为.
由几何关系,利用勾股定理,
得,解得.
.
.
故答案为:.
【分析】【类比思考】题目根据题意,按照【学习材料】中给定的解题方法求解即可;
【拓展应用】已知一次函数的图象与直线关于x轴对称,则直线上的点关于x轴对称的点的坐标为(x,-y),代入整理求解即可;
设直线m的解析式为y=ax+c,点(3,0)和(0,c)在直线m上,将(3,0)代入y=ax+c,利用勾股定理求解c,将a、c的值代回y=ax+c求解即可.
23.【答案】(1)解:由y=kx+2k+4,得y﹣4=k(x+2),
∵直线l:y=kx+2k+4过定点D,
∴x与y的值与k无关,
∴,
解得,
∴D(﹣2,4),
∴正方形ABCD的边长为4
(2)解:如图,连接BD,取BD中点E,连EM,EA,
∵在正方形ABCD中,正方形ABCD的边长为4,
∴AB=AD=4,∠DAB=90°,
∴BD= ,DN=AB=2,
∵点M、E分别为BN、BD的中点,
∴EM=DN=1,
∵∠DAB=90°,点E为BD的中点,
∴AE=BD=,
当点A、M、E三点不共线时,
在AME中,AM>AE-ME=-1,
当点A、M、E三点共线时,AM=AE-ME=-1,
∴AM≥-1,
∴当点A、M、E三点共线时,AM有最小值为-1;
此时,如下图,过点N作NF⊥x轴于点F,则NF∥AD,
设N(x,y),
∴
∴
∴
解得NF=PF=4﹣,
∴OF=OA+AP﹣PF
=2+4﹣(4﹣)
=2+
∴此时N(﹣2﹣,4﹣).
(3)解:如图,当点Q与点D重合,点P与点A重合,点E与点B重合,
此时四边形PQCE为正方形ADCB,符合题意,
此时直线CQ的解析式为:y=4;
如图,当点Q在x轴下方时,
∵四边形PQCE为菱形,
∴QP=QC=CE=EP,CQ∥PE,
∵PE⊥DP,
∴CQ⊥DP,
∴∠1+∠3=90°,
∵∠ADC=90°,
∴∠1+∠2=90°,
∴∠2=∠3,
又∵∠CDA=∠DAB=90°,CD=AD,
∴CDQ≌DAP(AAS),
∴CQ=DP,
又∵PQ=CQ,
∴PQ=PD,
∵PA⊥DQ,
∴AQ=AD=4,
∴点Q(-2,-4),
又∵C(2,4),
∴设直线CQ为y=kx+b,
则
解得
∴直线CQ:y=2x.
综上所述,四边形PQCE可以为菱形,此时直线CQ的解析式为y=4或y=2x.
【解析】【分析】(1)由y=kx+2k+4变形得y﹣4=k(x+2),根据直线过定点D,可知 x与y的值与k无关,得到 ,解方程组得到点D的坐标,即可得出正方形的边长;
(2)连接BD,取BD中点E,连EM,EA, 先根据正方形的性质及勾股定理求出DN的长,再根据三角形中位线定理可得EM=1,再根据三角形的两边之和大于第三边得出 AM>AE-ME ,进而可得当点A、M、E三点共线时,AM有最小值-1;过点N作NF⊥x轴于点F,则NF∥AD,设N(x,y),由建立方程求出 F=PF=4﹣, 进而得出OF的长,据此可得点N的坐标;
(3) 分两种情况讨论,当点Q与点D重合,点P与点A重合,点E与点B重合, 符合题意, 结合正方形的边长可知直线CQ的解析式为y=4; 当点Q在x轴下方时, 先证CDQ≌DAP,根据全等三角形的性质得到 CQ=DP, 进而得到点Q的坐标为(-2,-4),再结合点C的坐标,利用待定系数法求 直线CQ的解析式即可.
1 / 1
