六年级下册数学人教版(小升初)四则混合运算及简便计算(课件)(共45张PPT)
文档属性
| 名称 | 六年级下册数学人教版(小升初)四则混合运算及简便计算(课件)(共45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1021.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 13:42:09 | ||
图片预览







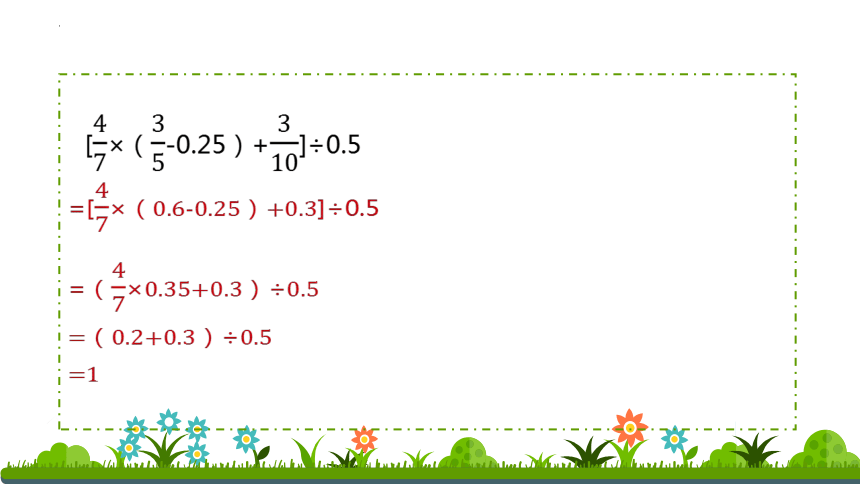



文档简介
(共45张PPT)
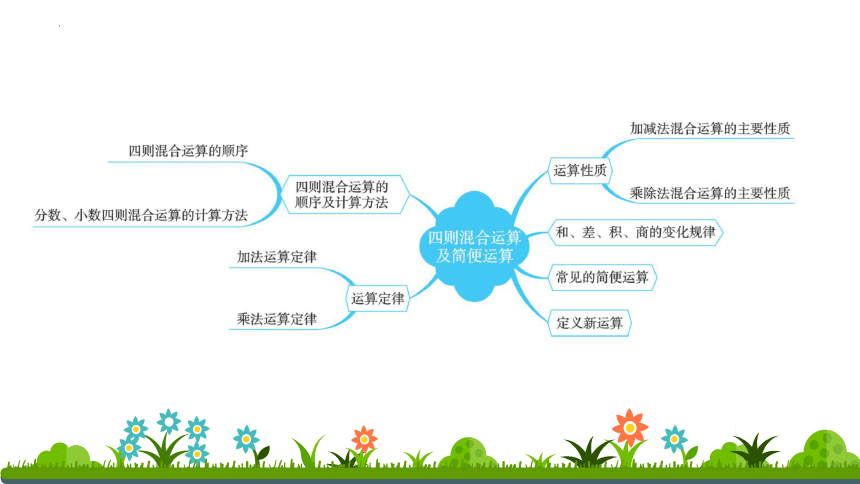
第3节 四则混合运算及简便计算
知识梳理 夯基提能
1.四则混合运算的顺序
(1)在没有括号的算式里,如果只含有加、减运算或只含有乘、除运算,就从左往右依次计算。
(2)在没有括号的算式里,如果既含有加、减运算,又含有乘、除运算,要先算乘法或除法,后算加法或减法。
(3)在有括号的算式里,先算小括号里面的,再算中括号里面的,最后算括号外面的。
知识点1 四则混合运算的顺序及计算方法
2.分数、小数四则混合运算的计算方法
分数、小数四则混合运算的题目,应该根据数字特征,灵活选择合理、简便的方法进行计算。
(1)分数、小数加减混合运算,分数能转化成有限小数(分母只含有质因数2和5)时,一般把分数化成小数后计算(避免了繁琐的通分);当分数不能化成有限小数时,就把小数化成分数。
(2)分数、小数乘法混合运算,如果小数与分数的分母能约分,可直接运算或把小数化成分数后再计算比较简便;如果把分数化成小数后能进行简算,也可以把分数化成小数计算。
(3)有些题目,不一定把全题统一化成分数或统一化成小数计算,可以根据运算顺序,分成几部分进行处理,选择合适的算法。
学霸笔记
可采用“看、想、画、查”四步骤进行四则计算,即“看算式中有哪些运算符号,想想怎样算合理,能否简便,画出运算顺序标出步骤;查运算数字、符号是否有错误”,提高计算准确率。
对应训练
1.把5.7+2.8=8.5,0.7×8.5=5.95,15.47÷5.95=2.6三个算式写成综合算式是 。
15.47÷[0.7×(5.7+2.8)]=2.6
2.脱式计算。
7375+884÷26×25 [9.2+80%×(9-7.75)]÷40%
=7375+34×25
=7375+850
=8225
=(9.2+80%×1.25)÷40%
=(9.2+1)÷40%
=10.2÷0.4
=25.5
[×(-0.25)+]÷0.5
=[×(0.6-0.25)+0.3]÷0.5
=(×0.35+0.3)÷0.5
=(0.2+0.3)÷0.5
=1
1.加法运算定律
(1)加法交换律:a+b=b+a
(2)加法结合律:(a+b)+c=a+(b+c)
2.乘法运算定律
(1)乘法交换律:a×b=b×a
(2)乘法结合律:(a×b)×c=a×(b×c)
(3)乘法分配律:(a+b)×c=a×c+b×c
知识点2 运算定律
学霸笔记
乘法分配律一般包括(a+b)×c=a×c+b×c与c×(a+b)=c×a+c×b这两种情况。如果把上式的结果与条件互换位置,就是乘法分配律的逆运用,定律仍旧成立,即a×c+b×c=(a+b)×c。此外,乘法分配律还可以推广到若干个数的和与一个数相乘的情况。
1.加减法混合运算的主要性质
(1)在加、减法混合运算中,改变运算的顺序,结果不变,即a-b+c=a+c-b。
(2)一个数加上两个数的差,等于这个数加上差里的被减数,再减去差里的减数,即a+(b-c)=a+b-c。
(3)一个数减去两个数的和,等于这个数依次减去和里的两个加数,即a-(b+c)=a-b-c。
知识点3 运算性质
(4)一个数减去两个数的差,等于这个数减去差里的被减数,再加上差里的减数,即a-(b-c)=a-b+c。
2.乘除法混合运算的主要性质
(1)在乘、除混合运算中,改变运算的顺序,结果不变,即a×b÷c=a÷c×b。
(2)一个数乘两个数的商,可以先把这个数乘商里的被除数,再除以商里的除数,即a×(b÷c)=a×b÷c。
(3)一个数除以两个数的积,可以把这个数依次除以积里的各个乘数,即a÷(b×c)=a÷b÷c。
(4)一个数除以两个数的商,等于这个数除以商里的被除数,再乘商里的除数,即a÷(b÷c)=a÷b×c。
(5)两个数的和(或差)除以一个数,可以用这个数分别去除和(或差)里的各个加数(或被减数、减数),再把各个商相加(或相减),即(a±b)÷c=a÷c±b÷c。
知识点4 和、差、积、商的变化规律
类别 变化规律 用字母表示
和 一个加数不变,另一个加数加上(或减去)一个数,和也要加上(或减去)同一个数。 若a+b=c,则(a±m)+b=c±m,a+(b±m)=c±m
一个加数加上(或减去)一个数,另一个加数反而减去(或加上)同一个数,它们的和不变。 若a+b=c,则(a+m)+(b-m)=c,(a-m)+(b+m)=c
差 减数不变,被减数加上(或减去)一个数,它们的差也要加上(或减去)同一个数。 若a-b=c,则(a+m)-b=c+m,
(a-m)-b=c-m
被减数不变,减数加上(或减去)一个数,它们的差反而要减去(或加上)同一个数。 若a-b=c,则a-(b+m)=c-m,
a-(b-m)=c+m
被减数和减数同时加上(或减去)同一个数,它们的差不变。 若a-b=c,则(a+m)-(b+m)=c,(a-m)-(b-m)=c
积 一个因数乘(或除以)一个数(0除外),另一个因数不变,它们的积也要乘(或除以)同一个数。 若a×b=c,则(a×m)×b=c×m,(a÷m)×b=c÷m(m≠0)
一个因数乘(或除以)一个数(0除外),另一个因数反而除以(或乘)同一个数,它们的积不变。 若a×b=c,则(a×m)×(b÷m)=c,
(a÷m)×(b×m)=c(m≠0)
商 除数不变,被除数乘(或除以)一个数(0除外),它们的商也要乘(或除以)同一个数。 若a÷b=c,则(a×m)÷b=c×m,
(a÷m)÷b=c÷m(b≠0,m≠0)
被除数不变,除数乘(或除以)一个数(0除外),它们的商反而要除以(或乘)这个数。 若a÷b=c,则a÷(b×m)=c÷m,a÷(b÷m)=c×m(b≠0,m≠0)
被除数和除数同时乘(或除以)同一个数(0除外),它们的商不变。 若a÷b=c,则(a×m)÷(b×m)=c,(a÷m)÷(b÷m)=c(b≠0,m≠0)
学霸笔记
在有余数的除法里,如果被除数和除数同时扩大到原来的几倍或缩小到原来的几分之一,它们的商不变,但余数要同时扩大到原来的几倍或缩小到原来的几分之一。如:640÷50=12……40,则6400÷500=12……400,64÷5=12……4。
1.拆数凑整法
对于算式中接近整十、整百……的数,通过转化使其变成整十、整百……的数加或减一个数的形式,可使计算简便。如:536-198=536-(200-2)=536-200+2=338,44×101=44×(100+1)=44×100+44=4444。
2.分组凑整法
对算式中的数进行重新整合,使之能利用运算定律、运算性质进行简算。如:152+637+248+72+28-137=(152+248)+(637-137)+(72+28)=400+500+100=1000。
知识点5 常见的简便运算
3.分解法
在某些乘、除法算式中,可以把其中的某个数进行分解,使计算简便。如:560÷35=560÷(7×5)=560÷7÷5=80÷5=16。
4.基准数法
若干个接近某数的数相加,可以先把某数作为基准数,然后把基准数与相加数的个数相乘,再加上(或减去)各数比基准数大(或小)的数,就可以得到计算结果。如:81+85+82+78+79=80×5+(1+5+2-2-1)=400+5=405。
典例1 下面各题怎样算简便就怎样算。
(1)7.2×87.5+87.5×1.8+87.5 (2)125×25×32
(3)÷46+÷ (4)999×222+333×334
【解析】本题主要考查运算定律与运算性质的综合运用。(1)逆用乘法分配律,把最后一个87.5看作87.5×1;(2)可把32分解成“4×8”,再根据乘法的交换律和结合律进行简便计算。(3)46分解成2×23,23和互为倒数,的分母和的分子相同,所以可以根据上述数据特点作为转化的起点,然后逆用乘法分配律进行简便计算。(4)999是333的倍数,将999×222转化为333×3×222=333×666,再根据乘法分配律求出结果。
【答案】 (1)原式=87.5×(7.2+1.8+1)=87.5×10=875
(2)原式=125×25×(4×8)=(125×8)×(25×4)=1000×100=100000
(3)原式=÷2÷23+×=+××(+)=
(4)原式=333×3×222+333×334=333×(666+334)=333000
对应训练
3.用你喜欢的方法计算。
××÷ ( + -)×48
=(×)×(×13)
=×2
=
=×48+×48-×48
=14+4-15
=3
185× -2×
=×(185-15)
=×170
=20
1.定义新运算是指用符号和已知运算表达式表示的一种新的运算。
2.定义新运算的计算方法和步骤:先正确理解新定义的算式的含义,再按照新运算的定义进行代换,从而将原式转化为一般的四则混合运算进行计算。
知识点6 定义新运算
典例2 已知A△B=A×B+A,那么(6△2.5)△4=( )。
[解析] “△”代表一种新运算符号:A△B=A×B+A,在新定义运算中同样规定要先算小括号里的,在计算(6△2.5)△4时,先计算(6△2.5),计算出结果再和4计算。6△2.5=6×2.5+6=21,21△4=21×4+21=105。
105
4.已知A△B=A×B-3A+4B,则5△7=( )。
5.我们定义一种运算“ ”:a b= ,其中m是一个常数。已知1 4=2 3,则3 4=( )。
48
对应训练
学以致用 随堂练习
一、填空。
1.两个数相加,如果一个加数增加10,要使和增加2,那么另一个加数应该( )。
2.两个数相减,如果被减数增加8,减数减少8,那么差应该( )。
3.两个因数的积是0.85,若一个因数扩大到原来的6倍,另一个因数缩小到原来的,则积是( )。
减少8
增加16
1.275
4.在a÷b=5……3中,把a,b同时扩大到原来的3倍之后,商和余数的和是( )。
5.已知A※B=AB-2B,可知5※(4※1)=( )。
14
6
二、选择。(把正确答案的序号填在括号里)
1.算式[190+(16-7)×15]÷(88-63)的运算顺序是( )。
B
2.计算(8.42+4.21+4.21)×2.5,下面几种计算方法中最简便的方法是( )。
A.8.42×2.5+4.21×2.5+4.21×2.5
B.(8.42+4.21×2)×2.5
C.4.21×(2+1+1)×2.5
D.4.21×[(2+1+1)×2.5]
D
3.650÷25=(650×4)÷(25×4)=2600÷100=26,此题的计算过程运用了( )。
A.乘法结合律 B.积不变的规律
C.乘法分配律 D.商不变的规律
4.小马虎在计算4(x+6)时看漏了括号,按4x+6计算,结果比原来( )。
A.少18 B.多x C.多6 D.少6
D
A
5.已知a,b,c,d都是非0的自然数,设m=a÷b×c÷d,那么与m不相等的算式是( )。
A.a÷(b×c)÷d B.a÷(b÷c)÷d
C.a×(c÷b÷d) D.c÷(b×d)×a
A
三、计算。
1.用简便方法计算。
(1)12.78-(1.78-1.24)+6.76
=(12.78-1.78)+(1.24+6.76)
=11+8
=19
(2)10000÷125÷25÷8÷5
=10000÷(125×8)÷(25×5)
=10÷125
=0.08
(3)4.85÷-3.6+6.15×3
=4.85×3.6-3.6×1+6.15×3.6
=3.6×(4.85-1+6.15)
=3.6×10
=36
(4)12.5×0.0275+1.25×0.425+12.5%
=0.125×(2.75+4.25+1)
=0.125×8
=1
2.按要求完成下面各题。
(1)7÷(+)<2□0.8,在□里应填的运算符号是( )。
(2)根据以下运算顺序,在算式-×+合适的位置添括号,并计算出来。
①乘→加→减 ②加→乘→减
÷(或+)
-(×+)=
-×(+)=
(3)38除以8的商减去4.3的差的倍是多少?
(38÷8-4.3)×=
四、解决问题。
1.
=-+-+-+-+-
=-=
2.用简便方法计算:+9+99+999+9999
=1-+10-+100-+1000-+10000-
=(1+10+100+1000+10000)-×5
=11111-1
=11110
3.某校六年级学生在六一儿童节当天开展“禹州方山寨豫西抗战纪念馆”参观活动,共用去5小时,其中路上用去的时间占,吃午饭和休息的时间共占,剩下的是参观学习的时间。参观学习的时间比路上用去的时间多几小时?
5×[(1--)-]=(小时)
答:参观学习的时间比路上用去的时间多小时。
第3节 四则混合运算及简便计算
知识梳理 夯基提能
1.四则混合运算的顺序
(1)在没有括号的算式里,如果只含有加、减运算或只含有乘、除运算,就从左往右依次计算。
(2)在没有括号的算式里,如果既含有加、减运算,又含有乘、除运算,要先算乘法或除法,后算加法或减法。
(3)在有括号的算式里,先算小括号里面的,再算中括号里面的,最后算括号外面的。
知识点1 四则混合运算的顺序及计算方法
2.分数、小数四则混合运算的计算方法
分数、小数四则混合运算的题目,应该根据数字特征,灵活选择合理、简便的方法进行计算。
(1)分数、小数加减混合运算,分数能转化成有限小数(分母只含有质因数2和5)时,一般把分数化成小数后计算(避免了繁琐的通分);当分数不能化成有限小数时,就把小数化成分数。
(2)分数、小数乘法混合运算,如果小数与分数的分母能约分,可直接运算或把小数化成分数后再计算比较简便;如果把分数化成小数后能进行简算,也可以把分数化成小数计算。
(3)有些题目,不一定把全题统一化成分数或统一化成小数计算,可以根据运算顺序,分成几部分进行处理,选择合适的算法。
学霸笔记
可采用“看、想、画、查”四步骤进行四则计算,即“看算式中有哪些运算符号,想想怎样算合理,能否简便,画出运算顺序标出步骤;查运算数字、符号是否有错误”,提高计算准确率。
对应训练
1.把5.7+2.8=8.5,0.7×8.5=5.95,15.47÷5.95=2.6三个算式写成综合算式是 。
15.47÷[0.7×(5.7+2.8)]=2.6
2.脱式计算。
7375+884÷26×25 [9.2+80%×(9-7.75)]÷40%
=7375+34×25
=7375+850
=8225
=(9.2+80%×1.25)÷40%
=(9.2+1)÷40%
=10.2÷0.4
=25.5
[×(-0.25)+]÷0.5
=[×(0.6-0.25)+0.3]÷0.5
=(×0.35+0.3)÷0.5
=(0.2+0.3)÷0.5
=1
1.加法运算定律
(1)加法交换律:a+b=b+a
(2)加法结合律:(a+b)+c=a+(b+c)
2.乘法运算定律
(1)乘法交换律:a×b=b×a
(2)乘法结合律:(a×b)×c=a×(b×c)
(3)乘法分配律:(a+b)×c=a×c+b×c
知识点2 运算定律
学霸笔记
乘法分配律一般包括(a+b)×c=a×c+b×c与c×(a+b)=c×a+c×b这两种情况。如果把上式的结果与条件互换位置,就是乘法分配律的逆运用,定律仍旧成立,即a×c+b×c=(a+b)×c。此外,乘法分配律还可以推广到若干个数的和与一个数相乘的情况。
1.加减法混合运算的主要性质
(1)在加、减法混合运算中,改变运算的顺序,结果不变,即a-b+c=a+c-b。
(2)一个数加上两个数的差,等于这个数加上差里的被减数,再减去差里的减数,即a+(b-c)=a+b-c。
(3)一个数减去两个数的和,等于这个数依次减去和里的两个加数,即a-(b+c)=a-b-c。
知识点3 运算性质
(4)一个数减去两个数的差,等于这个数减去差里的被减数,再加上差里的减数,即a-(b-c)=a-b+c。
2.乘除法混合运算的主要性质
(1)在乘、除混合运算中,改变运算的顺序,结果不变,即a×b÷c=a÷c×b。
(2)一个数乘两个数的商,可以先把这个数乘商里的被除数,再除以商里的除数,即a×(b÷c)=a×b÷c。
(3)一个数除以两个数的积,可以把这个数依次除以积里的各个乘数,即a÷(b×c)=a÷b÷c。
(4)一个数除以两个数的商,等于这个数除以商里的被除数,再乘商里的除数,即a÷(b÷c)=a÷b×c。
(5)两个数的和(或差)除以一个数,可以用这个数分别去除和(或差)里的各个加数(或被减数、减数),再把各个商相加(或相减),即(a±b)÷c=a÷c±b÷c。
知识点4 和、差、积、商的变化规律
类别 变化规律 用字母表示
和 一个加数不变,另一个加数加上(或减去)一个数,和也要加上(或减去)同一个数。 若a+b=c,则(a±m)+b=c±m,a+(b±m)=c±m
一个加数加上(或减去)一个数,另一个加数反而减去(或加上)同一个数,它们的和不变。 若a+b=c,则(a+m)+(b-m)=c,(a-m)+(b+m)=c
差 减数不变,被减数加上(或减去)一个数,它们的差也要加上(或减去)同一个数。 若a-b=c,则(a+m)-b=c+m,
(a-m)-b=c-m
被减数不变,减数加上(或减去)一个数,它们的差反而要减去(或加上)同一个数。 若a-b=c,则a-(b+m)=c-m,
a-(b-m)=c+m
被减数和减数同时加上(或减去)同一个数,它们的差不变。 若a-b=c,则(a+m)-(b+m)=c,(a-m)-(b-m)=c
积 一个因数乘(或除以)一个数(0除外),另一个因数不变,它们的积也要乘(或除以)同一个数。 若a×b=c,则(a×m)×b=c×m,(a÷m)×b=c÷m(m≠0)
一个因数乘(或除以)一个数(0除外),另一个因数反而除以(或乘)同一个数,它们的积不变。 若a×b=c,则(a×m)×(b÷m)=c,
(a÷m)×(b×m)=c(m≠0)
商 除数不变,被除数乘(或除以)一个数(0除外),它们的商也要乘(或除以)同一个数。 若a÷b=c,则(a×m)÷b=c×m,
(a÷m)÷b=c÷m(b≠0,m≠0)
被除数不变,除数乘(或除以)一个数(0除外),它们的商反而要除以(或乘)这个数。 若a÷b=c,则a÷(b×m)=c÷m,a÷(b÷m)=c×m(b≠0,m≠0)
被除数和除数同时乘(或除以)同一个数(0除外),它们的商不变。 若a÷b=c,则(a×m)÷(b×m)=c,(a÷m)÷(b÷m)=c(b≠0,m≠0)
学霸笔记
在有余数的除法里,如果被除数和除数同时扩大到原来的几倍或缩小到原来的几分之一,它们的商不变,但余数要同时扩大到原来的几倍或缩小到原来的几分之一。如:640÷50=12……40,则6400÷500=12……400,64÷5=12……4。
1.拆数凑整法
对于算式中接近整十、整百……的数,通过转化使其变成整十、整百……的数加或减一个数的形式,可使计算简便。如:536-198=536-(200-2)=536-200+2=338,44×101=44×(100+1)=44×100+44=4444。
2.分组凑整法
对算式中的数进行重新整合,使之能利用运算定律、运算性质进行简算。如:152+637+248+72+28-137=(152+248)+(637-137)+(72+28)=400+500+100=1000。
知识点5 常见的简便运算
3.分解法
在某些乘、除法算式中,可以把其中的某个数进行分解,使计算简便。如:560÷35=560÷(7×5)=560÷7÷5=80÷5=16。
4.基准数法
若干个接近某数的数相加,可以先把某数作为基准数,然后把基准数与相加数的个数相乘,再加上(或减去)各数比基准数大(或小)的数,就可以得到计算结果。如:81+85+82+78+79=80×5+(1+5+2-2-1)=400+5=405。
典例1 下面各题怎样算简便就怎样算。
(1)7.2×87.5+87.5×1.8+87.5 (2)125×25×32
(3)÷46+÷ (4)999×222+333×334
【解析】本题主要考查运算定律与运算性质的综合运用。(1)逆用乘法分配律,把最后一个87.5看作87.5×1;(2)可把32分解成“4×8”,再根据乘法的交换律和结合律进行简便计算。(3)46分解成2×23,23和互为倒数,的分母和的分子相同,所以可以根据上述数据特点作为转化的起点,然后逆用乘法分配律进行简便计算。(4)999是333的倍数,将999×222转化为333×3×222=333×666,再根据乘法分配律求出结果。
【答案】 (1)原式=87.5×(7.2+1.8+1)=87.5×10=875
(2)原式=125×25×(4×8)=(125×8)×(25×4)=1000×100=100000
(3)原式=÷2÷23+×=+××(+)=
(4)原式=333×3×222+333×334=333×(666+334)=333000
对应训练
3.用你喜欢的方法计算。
××÷ ( + -)×48
=(×)×(×13)
=×2
=
=×48+×48-×48
=14+4-15
=3
185× -2×
=×(185-15)
=×170
=20
1.定义新运算是指用符号和已知运算表达式表示的一种新的运算。
2.定义新运算的计算方法和步骤:先正确理解新定义的算式的含义,再按照新运算的定义进行代换,从而将原式转化为一般的四则混合运算进行计算。
知识点6 定义新运算
典例2 已知A△B=A×B+A,那么(6△2.5)△4=( )。
[解析] “△”代表一种新运算符号:A△B=A×B+A,在新定义运算中同样规定要先算小括号里的,在计算(6△2.5)△4时,先计算(6△2.5),计算出结果再和4计算。6△2.5=6×2.5+6=21,21△4=21×4+21=105。
105
4.已知A△B=A×B-3A+4B,则5△7=( )。
5.我们定义一种运算“ ”:a b= ,其中m是一个常数。已知1 4=2 3,则3 4=( )。
48
对应训练
学以致用 随堂练习
一、填空。
1.两个数相加,如果一个加数增加10,要使和增加2,那么另一个加数应该( )。
2.两个数相减,如果被减数增加8,减数减少8,那么差应该( )。
3.两个因数的积是0.85,若一个因数扩大到原来的6倍,另一个因数缩小到原来的,则积是( )。
减少8
增加16
1.275
4.在a÷b=5……3中,把a,b同时扩大到原来的3倍之后,商和余数的和是( )。
5.已知A※B=AB-2B,可知5※(4※1)=( )。
14
6
二、选择。(把正确答案的序号填在括号里)
1.算式[190+(16-7)×15]÷(88-63)的运算顺序是( )。
B
2.计算(8.42+4.21+4.21)×2.5,下面几种计算方法中最简便的方法是( )。
A.8.42×2.5+4.21×2.5+4.21×2.5
B.(8.42+4.21×2)×2.5
C.4.21×(2+1+1)×2.5
D.4.21×[(2+1+1)×2.5]
D
3.650÷25=(650×4)÷(25×4)=2600÷100=26,此题的计算过程运用了( )。
A.乘法结合律 B.积不变的规律
C.乘法分配律 D.商不变的规律
4.小马虎在计算4(x+6)时看漏了括号,按4x+6计算,结果比原来( )。
A.少18 B.多x C.多6 D.少6
D
A
5.已知a,b,c,d都是非0的自然数,设m=a÷b×c÷d,那么与m不相等的算式是( )。
A.a÷(b×c)÷d B.a÷(b÷c)÷d
C.a×(c÷b÷d) D.c÷(b×d)×a
A
三、计算。
1.用简便方法计算。
(1)12.78-(1.78-1.24)+6.76
=(12.78-1.78)+(1.24+6.76)
=11+8
=19
(2)10000÷125÷25÷8÷5
=10000÷(125×8)÷(25×5)
=10÷125
=0.08
(3)4.85÷-3.6+6.15×3
=4.85×3.6-3.6×1+6.15×3.6
=3.6×(4.85-1+6.15)
=3.6×10
=36
(4)12.5×0.0275+1.25×0.425+12.5%
=0.125×(2.75+4.25+1)
=0.125×8
=1
2.按要求完成下面各题。
(1)7÷(+)<2□0.8,在□里应填的运算符号是( )。
(2)根据以下运算顺序,在算式-×+合适的位置添括号,并计算出来。
①乘→加→减 ②加→乘→减
÷(或+)
-(×+)=
-×(+)=
(3)38除以8的商减去4.3的差的倍是多少?
(38÷8-4.3)×=
四、解决问题。
1.
=-+-+-+-+-
=-=
2.用简便方法计算:+9+99+999+9999
=1-+10-+100-+1000-+10000-
=(1+10+100+1000+10000)-×5
=11111-1
=11110
3.某校六年级学生在六一儿童节当天开展“禹州方山寨豫西抗战纪念馆”参观活动,共用去5小时,其中路上用去的时间占,吃午饭和休息的时间共占,剩下的是参观学习的时间。参观学习的时间比路上用去的时间多几小时?
5×[(1--)-]=(小时)
答:参观学习的时间比路上用去的时间多小时。
同课章节目录
