北师大版四年级数学上册第四单元《加法交换律和乘法交换律》课件(共21张PPT)
文档属性
| 名称 | 北师大版四年级数学上册第四单元《加法交换律和乘法交换律》课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 14:24:56 | ||
图片预览





文档简介
(共21张PPT)
加法交换律
和
乘法交换律
狙公懂得猴子的心理,猴子也了解他的话,因此,他更加的疼爱这些能通人语的小动物,经常缩减家中的口粮,来满足猴子的食欲。
他说:“从明天开始,我每天早上给你们3颗果子,晚上再给你们4颗,好吗?”
猴子们听说他们的食粮减少,都咧嘴露牙的站了起来,表现出非常生气的样子。
狙公看了,马上就改口说:“这样好了,我每天早上给你们4颗,晚上再给你们3颗,够吃了吧!”
猴子们听说早上己经从三颗变成了四颗,以为食粮已经增加了,都非常高兴,不再闹了。
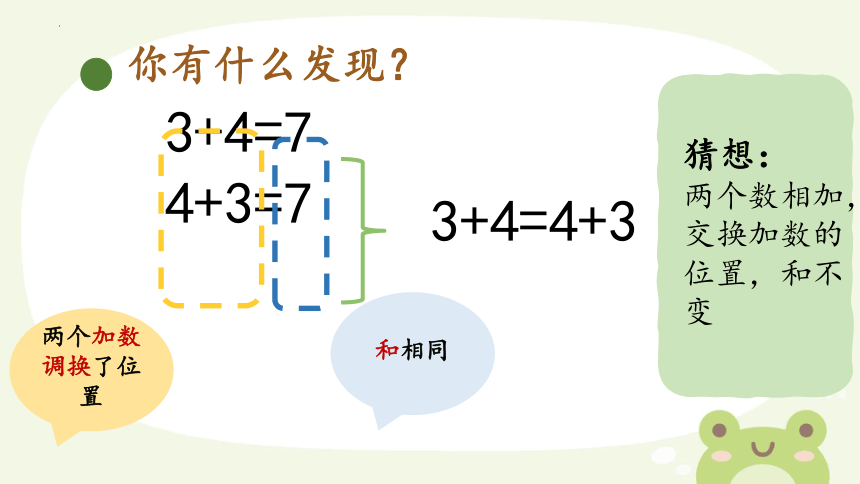
3+4=7
4+3=7
你有什么发现?
3+4=4+3
两个加数调换了位置
和相同
猜想:
两个数相加,交换加数的位置,和不变
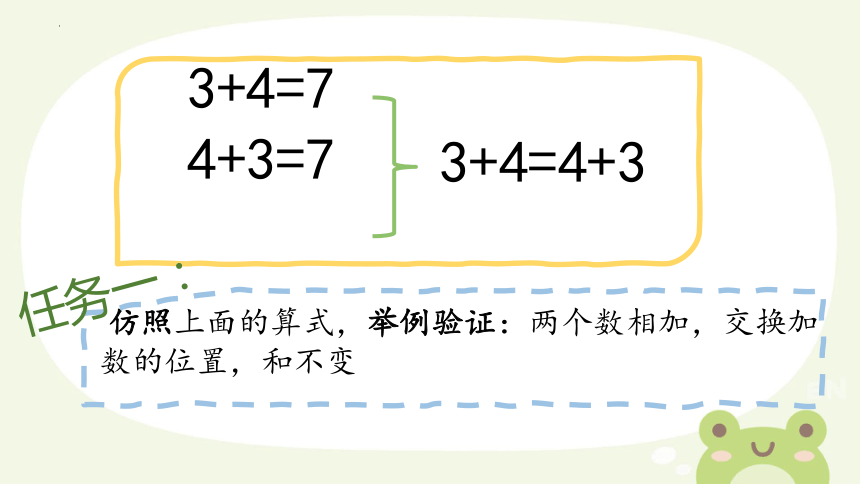
3+4=7
4+3=7
3+4=4+3
仿照上面的算式,举例验证:两个数相加,交换加数的位置,和不变
任务一:
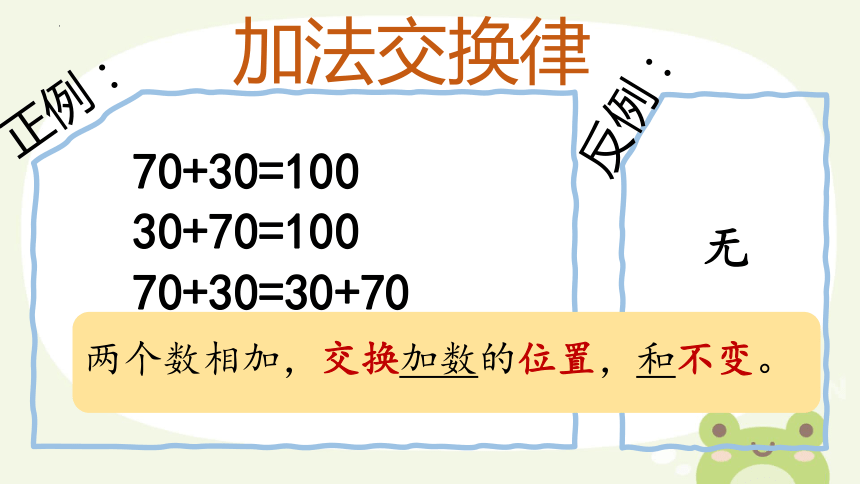
反例:
正例:
加法交换律
70+30=100
30+70=100
70+30=30+70
无
两个数相加,交换加数的位置,和不变。
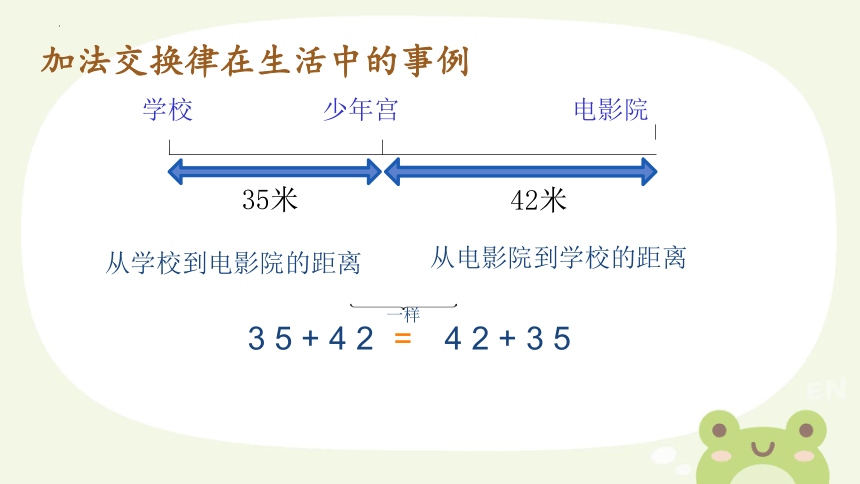
学校 少年宫 电影院
35米
42米
加法交换律在生活中的事例
从学校到电影院的距离
从电影院到学校的距离
3 5 + 4 2
4 2 + 3 5
一样
=
a+b=b+a
+
=
+
甲数+乙数=乙数+甲数
能写一个万能的式子表示出规律吗?用一些你喜欢的符号或字母表示这个规律
交换两个数的位置
加法
和不变
乘法
积?
除法
商?
减法
差?
①分别在减法、除法、乘法运算中,交换两个数的位置进行探究。
②如果存在交换律,请举例验证并总结。
任务二:
减法、除法、乘法中也有交换律吗?
反例:
正例:
存在减法交换律吗?
不存在
1-1=0
1-1=0
1-1=1-1
99-99=0
99-99=0
99-99=99-99
6-3=3
3-6≠3
6-3≠3-6
反例:
正例:
存在除法交换律吗?
18÷9=2
9÷18≠2
18÷9≠9÷18
21÷21=1
21÷21=1
21÷21=21÷21
不存在
反例:
正例:
存在乘法交换律吗?
6×9=54
9×6=54
6×9=9×6
无
存在
加法交换律
乘法交换律
两个数相加,交换加数的位置,和不变
两个数相乘,交换乘数的位置,积不变
a+b=b+a
a×b=b×a
一共有多少把椅子?
算法一:6×5=30(把)
算法二:5×6=30(把)
所以:6×5 = 5×6
乘法交换律在生活中的事例
你能结合今天学习的知识解释下面计算的道理吗?
利用乘法交换律,计算更简便
利用加法交换律验算
如果换成三个数,四个数甚至更多的数相加、相乘,交换它们的位置,它们的和或积会不会也不变呢?
是否还存在加法交换律或乘法交换律呢?
思考:
1.结合下面的例子说明等式为什么成立。
2.运用加法交换律和乘法交换律填一填。
45 + 76 = + 45
45×102 = 102 ×
296 × 200 =
28 + 13 = +
+ = +
× = ×
76
45
13
28
15
82
82
15
64
32
32
64
×
200
296
3.列竖式计算下列各题,并运用加法交换律或乘法交换律进行验算。
918+395
35×27
9 1 8
+ 3 9 5
1 3 1 3
验
算:
3 9 5
+ 9 1 8
1 3 1 3
3 5
× 2 7
2 4 5
7 0
9 4 5
验
算:
2 7
× 3 5
1 3 5
8 1
9 4 5
加法交换律
和
乘法交换律
狙公懂得猴子的心理,猴子也了解他的话,因此,他更加的疼爱这些能通人语的小动物,经常缩减家中的口粮,来满足猴子的食欲。
他说:“从明天开始,我每天早上给你们3颗果子,晚上再给你们4颗,好吗?”
猴子们听说他们的食粮减少,都咧嘴露牙的站了起来,表现出非常生气的样子。
狙公看了,马上就改口说:“这样好了,我每天早上给你们4颗,晚上再给你们3颗,够吃了吧!”
猴子们听说早上己经从三颗变成了四颗,以为食粮已经增加了,都非常高兴,不再闹了。
3+4=7
4+3=7
你有什么发现?
3+4=4+3
两个加数调换了位置
和相同
猜想:
两个数相加,交换加数的位置,和不变
3+4=7
4+3=7
3+4=4+3
仿照上面的算式,举例验证:两个数相加,交换加数的位置,和不变
任务一:
反例:
正例:
加法交换律
70+30=100
30+70=100
70+30=30+70
无
两个数相加,交换加数的位置,和不变。
学校 少年宫 电影院
35米
42米
加法交换律在生活中的事例
从学校到电影院的距离
从电影院到学校的距离
3 5 + 4 2
4 2 + 3 5
一样
=
a+b=b+a
+
=
+
甲数+乙数=乙数+甲数
能写一个万能的式子表示出规律吗?用一些你喜欢的符号或字母表示这个规律
交换两个数的位置
加法
和不变
乘法
积?
除法
商?
减法
差?
①分别在减法、除法、乘法运算中,交换两个数的位置进行探究。
②如果存在交换律,请举例验证并总结。
任务二:
减法、除法、乘法中也有交换律吗?
反例:
正例:
存在减法交换律吗?
不存在
1-1=0
1-1=0
1-1=1-1
99-99=0
99-99=0
99-99=99-99
6-3=3
3-6≠3
6-3≠3-6
反例:
正例:
存在除法交换律吗?
18÷9=2
9÷18≠2
18÷9≠9÷18
21÷21=1
21÷21=1
21÷21=21÷21
不存在
反例:
正例:
存在乘法交换律吗?
6×9=54
9×6=54
6×9=9×6
无
存在
加法交换律
乘法交换律
两个数相加,交换加数的位置,和不变
两个数相乘,交换乘数的位置,积不变
a+b=b+a
a×b=b×a
一共有多少把椅子?
算法一:6×5=30(把)
算法二:5×6=30(把)
所以:6×5 = 5×6
乘法交换律在生活中的事例
你能结合今天学习的知识解释下面计算的道理吗?
利用乘法交换律,计算更简便
利用加法交换律验算
如果换成三个数,四个数甚至更多的数相加、相乘,交换它们的位置,它们的和或积会不会也不变呢?
是否还存在加法交换律或乘法交换律呢?
思考:
1.结合下面的例子说明等式为什么成立。
2.运用加法交换律和乘法交换律填一填。
45 + 76 = + 45
45×102 = 102 ×
296 × 200 =
28 + 13 = +
+ = +
× = ×
76
45
13
28
15
82
82
15
64
32
32
64
×
200
296
3.列竖式计算下列各题,并运用加法交换律或乘法交换律进行验算。
918+395
35×27
9 1 8
+ 3 9 5
1 3 1 3
验
算:
3 9 5
+ 9 1 8
1 3 1 3
3 5
× 2 7
2 4 5
7 0
9 4 5
验
算:
2 7
× 3 5
1 3 5
8 1
9 4 5
同课章节目录
- 一 认识更大的数
- 1 数一数
- 2 认识更大的数
- 3 人口普查
- 4 国土面积
- 5 近似数
- 6 从结绳计数说起
- 二 线与角
- 1 线的认识
- 2 相交与垂直
- 3 平移与平行
- 4 旋转与角
- 5 角的度量(一)
- 6 角的度量(二)
- 三 乘法
- 1 卫星运行时间
- 2 有多少名观众
- 3 神奇的计算工具
- 4 有趣的算式
- 四 运算律
- 1 买文具
- 2 加法交换律和乘法交换律
- 3 加法结合律
- 4 乘法结合律
- 5 乘法分配律
- 五 方向与位置
- 1 去图书馆
- 2 确定位置
- 六 除法
- 1 买文具
- 2 参观花圃
- 3 秋游
- 4 商不变的规律
- 5 路程、时间与速度
- 七 生活中的负数
- 1 温度
- 2 正负数
- 数学好玩
- 1 滴水试验
- 2 编码
- 3 数图形的学问
- 八 可能性
- 1 不确定性
- 2 摸球游戏
