第十章 10.3.2 随机模拟 课件(共20张PPT)
文档属性
| 名称 | 第十章 10.3.2 随机模拟 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-23 13:57:04 | ||
图片预览








文档简介
(共20张PPT)
第十章
10.3.2 随机模拟
人教A版(2019)
教学目标
学习目标 数学素养
1.了解随机数的意义,理解用模拟方法估计概率的实质. 1.数学建模素养和数据分析素养.
2.会用随机模拟方法估计概率. 2.数学建模素养和数学运算素养.
温故知新
1.频率的性质
2.频率与概率的区别与联系
频率 概率
区别 本身是随机的,是一个变量,在试验前不能确定. 是一个确定的数,是客观存在的,与每次的试验无关.
联系 随着试验次数的增加,频率逐渐稳定在概率附近,所以当试验次数比较大时,我们常常用频率估计概率. 一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率fn(A)会逐渐稳定于事件A发生的概率P(A).我们称频率的这个性质为频率的稳定性.
因此,我们可以用频率fn(A)估计概率P(A).
新知探究
我们知道,利用计算器或计算机软件可以产生随机数. 实际上,我们也可以根据不同的随机试验构建相应的随机数模拟试验,这样就可以快速地进行大量重复试验了.
用频率估计概率,需要做大量的重复试验.有没有其他方法可以替代试验呢
例如,对于抛掷一枚质地均匀硬币的试验,我们可以让计算器或计算机产生取值于集合{0, 1}的随机数,用0表示反面朝上,用1表示正面朝上,这样不断产生0, 1两个随机数,相当于不断地做拋掷硬币的试验.
又如,一个袋中装有2个红球和3个白球,这些球除颜色不同外没有其他差别,对于从袋中摸出一个球的试验,我们可以让计算器或计算机产生取值于集合{1, 2, 3, 4, 5}的随机数,用1, 2表示红球,用3, 4, 5表示白球. 这样不断产生1~5之间的整数随机数,相当于不断地做从袋中摸球的试验.
随机数与伪随机数
例如我们要产生1~9 之间的随机整数,像彩票摇奖那样,把10个质地和大小相同的号码球放入摇奖器中,充分搅拌后摇出一个球,这个球上的号码就称为随机数.计算器或计算机产生的随机数是按照确定的算法产生的数,具有周期性(周期很长),它们具有类似随机数的性质.因此,计算器或计算机产生的随机数不是真正的随机数,我们称它们为伪随机数.
新知探究
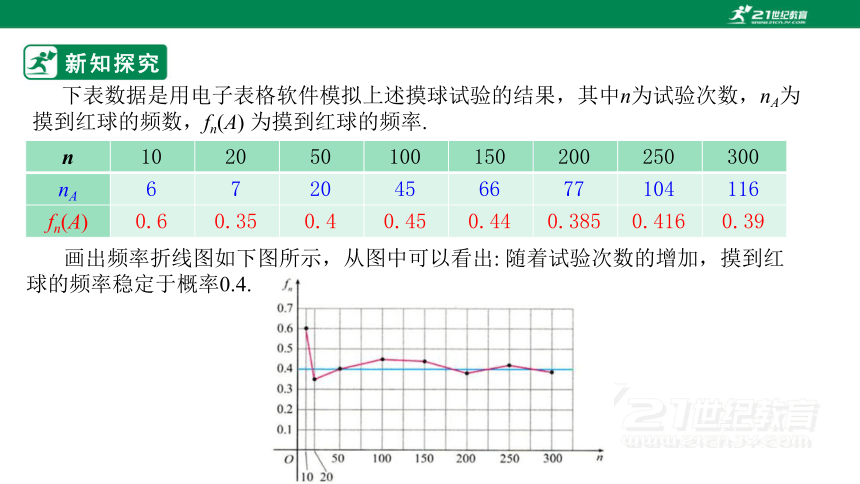
下表数据是用电子表格软件模拟上述摸球试验的结果,其中n为试验次数,nA为摸到红球的频数,fn(A) 为摸到红球的频率.
n 10 20 50 100 150 200 250 300
nA 6 7 20 45 66 77 104 116
fn(A) 0.6 0.35 0.4 0.45 0.44 0.385 0.416 0.39
画出频率折线图如下图所示,从图中可以看出: 随着试验次数的增加,摸到红球的频率稳定于概率0.4.
知新探究
我们称利用随机模拟解决问题的方法为蒙特卡洛(Monte Carlo)方法.
蒙特卡洛方法是在第二次世界大战期间兴起和发展起来的,它的奠基人是冯·诺依曼(John von Neumann).这种方法在应用物理、原子能、固体物理、化学、生物、生态学、社会学以及经济行为等领域中都得到了广泛的应用.
随机模拟方法是通过将一次试验所有可能发生的结果数字化,用计算机或计算器产生的随机数来替代每次试验的结果.
其基本思想是用产生整数随机数的频率估计事件发生的概率.
知新探究
【例3】从你所在班级任意选出6名同学,调查他们的出生月份,假设出生在一月,二月,…,十二月是等可能的.设事件A =“至少有两人出生月份相同”,设计一种试验方法,模拟20次,估计事件A发生的概率.
解:
方法1 根据假设,每个人的出生月份在12个月中是等可能的,而且相互之间没有影响,所以观察6个人的出生月份可以看成可重复试验.
在袋子中装入编号为1,2,…,12的12个球,这些球除编号外没有什么差别.有放回地随机从袋中摸6次球,得到6个数代表6个人的出生月份,这就完成了一次模拟试验.如果这6个数中至少有2个相同,表示事件A发生了.
因此,可以构建如下有放回摸球试验进行模拟:
重复以上模拟试验20次,就可以统计出事件A发生的频率.
知新探究
【例3】从你所在班级任意选出6名同学,调查他们的出生月份,假设出生在一月,二月,…,十二月是等可能的.设事件A =“至少有两人出生月份相同”,设计一种试验方法,模拟20次,估计事件A发生的概率.
解:
方法2 利用电子表格软件模拟试验. 在A1, B1, C1, D1, E1, F1 单元格分别输入“= RANDBETWEEN (1,12)”,得到6个数,代表6个人的出生月份,完成一次模拟试验. 选中Al, Bl, C1, D1, E1, F1单元格,将鼠标指向右下角的黑点,按住鼠标左键拖动到第20行,相当于做20次重复试验. 统计其中有相同数的频率,得到事件A的概率的估计值.
知新探究
随机模拟
上表是20次模拟试验的结果.事件A发生了14次,事件A的概率估计值为0.70,与事件A的概率(约0.78)相差不大.
知新探究
做整数随机模拟试验时应注意的相关事项:
⑴首先要确定随机数的范围,明确哪个数字代表哪个试验结果;
⑵当试验的基本结果的可能性相等时,基本事件总数即为产生随机数的范围,每个随机数代表一个基本事件;
⑶当研究等可能事件的概率时,用按比例分配的方法确定表示各个结果的数字个数及范围;
⑷当每次试验结果需要n个随机数表示时,要把n个随机数作为一组来处理,此时一定要注意每组中的随机数字能否重复.
知新探究
【例4】在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.利用计算机模拟试验,估计甲获得冠军的概率.
解:
分析:奥运会羽毛球比赛规则是3局2胜制,甲获得冠军的结果可能是2:0或2:1.显然,甲连胜2局或在前2局中赢一局输一局,并赢得第3局的概率,与打满3局,甲胜2局或3局的概率相同.每局比赛甲可能胜,也可能负,3局比赛所有可能结果有8种,但是每个结果不是等可能出现的,因此不是古典概型,可以用计算机模拟比赛结果.
由于要比赛3局, 所以每3个随机数为一组. 例如, 产生20组随机数:
设事件A=“甲获得冠军”,事件B=“单局比赛甲胜”,则P(B)=0.6.用计算器或计算机产生1~5之间的随机数,当出现随机数1、2或3时,表示一局比赛甲获胜,其概率为0.6.
423 123 423 344 114 453 525 332 152 342
534 443 512 541 125 432 334 151 314 354.
知新探究
【例4】在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.利用计算机模拟试验,估计甲获得冠军的概率.
解:
423, 123, 423, 114, 332, 152, 342, 512, 125,
432, 334, 151, 314,
相当于做了20次重复试验.其中事件A发生了13次,对应的数组分别是
423 123 423 344 114 453 525 332 152 342
534 443 512 541 125 432 334 151 314 354.
频率估计事件A的概率的近似为=0.65.
用随机模拟的方法得到的是20次试验中事件A发生的频率,事件A的概率的精确值为0.648.
知新探究
【例5】甲、乙两支篮球队进行一次比赛,采用三局两胜制.一局比赛中,甲获胜的概率为0.6,现用随机模拟的方法估计本次比赛乙获胜的概率.先利用计算器或计算机生成0~9之间取整数值的随机数,用0,1,2,3,4,5表示甲获胜,6,7,8,9表示乙获胜.因为采用三局两胜制,所以每3个随机数作为一组.例如,产生30组随机数:
034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959 774 246 762 428 114 572 042 533 237 322 707 360 751
据此估计乙获胜的概率为 .(结果保留到小数点后三位)
解:
如果6,7,8,9中恰有2个或3个数出现,就表示乙获胜,它们分别是738,636,964,736,698,637,616,959,774,762,707,共11个.
这30组数数据就相当于做了30次试验.
所以采用三局两胜制,乙获胜的概率约为0.367.
0.367
初试身手
1.西岳华山是著名的旅游胜地.天气预报称8月1日后连续四天,每天下雨的概率为0.6.现用随机模拟的方法估计四天中恰有三天下雨的概率:在0~9十个整数值中,假定0,1,2,3,4,5表示当天下雨,6,7,8,9表示当天不下雨.在随机数表中从某位置按从左到右的顺序读取如下40组四位随机数:
9533 9522 0018 7472 0018 3879 5869 3281 7890 2692
8280 8425 3990 8460 7980 2436 5987 3882 0753 8935
9635 2379 1805 9890 0735 4640 6298 8054 9720 5695
1574 8008 3216 6470 5080 6772 1642 7920 3189 0343
据此估计四天中恰有三天下雨的概率为( )
A. B. C. D.
在40组四位随机数中,0~5的整数恰好出现3次的四位数有16组,
解:
则四天中恰有三天下雨的概率的估计值为.故选B.
B
初试身手
1.将一枚质地均匀的硬币连掷4次,设事件A =“恰好两次正面朝上”.
⑴直接计算事件A的概率;
⑵利用计算器或计算机模拟试验80次,计算事件A发生的频率.(课本P260 练习 第1题)
⑴P(A)=.
解:
⑵用计算机产生1~2之间的随机数, 当出现随机数为1时表示硬币正面朝上, 当出现随机数为2时表示硬币反面朝上, 然后产生80个数字,计算事件A发生的频率.
课堂小结
1.产生随机数的方法
2.蒙特卡洛方法
利用计算器或计算机软件产生随机数;
构建模拟试验产生随机数.
利用随机模拟解决问题的方法为蒙特卡洛方法.
3.应用随机数估计概率的步骤:
⑴明确随机数的范围及数字与试验结果的对应关系.
⑵产生随机数.
⑶统计试验次数N及所求事件发生的次数n.
⑷计算即可.
作业布置
作业: P260 练习 第2,3题
P261 习题10.3 第2,3,4题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第十章
10.3.2 随机模拟
人教A版(2019)
教学目标
学习目标 数学素养
1.了解随机数的意义,理解用模拟方法估计概率的实质. 1.数学建模素养和数据分析素养.
2.会用随机模拟方法估计概率. 2.数学建模素养和数学运算素养.
温故知新
1.频率的性质
2.频率与概率的区别与联系
频率 概率
区别 本身是随机的,是一个变量,在试验前不能确定. 是一个确定的数,是客观存在的,与每次的试验无关.
联系 随着试验次数的增加,频率逐渐稳定在概率附近,所以当试验次数比较大时,我们常常用频率估计概率. 一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率fn(A)会逐渐稳定于事件A发生的概率P(A).我们称频率的这个性质为频率的稳定性.
因此,我们可以用频率fn(A)估计概率P(A).
新知探究
我们知道,利用计算器或计算机软件可以产生随机数. 实际上,我们也可以根据不同的随机试验构建相应的随机数模拟试验,这样就可以快速地进行大量重复试验了.
用频率估计概率,需要做大量的重复试验.有没有其他方法可以替代试验呢
例如,对于抛掷一枚质地均匀硬币的试验,我们可以让计算器或计算机产生取值于集合{0, 1}的随机数,用0表示反面朝上,用1表示正面朝上,这样不断产生0, 1两个随机数,相当于不断地做拋掷硬币的试验.
又如,一个袋中装有2个红球和3个白球,这些球除颜色不同外没有其他差别,对于从袋中摸出一个球的试验,我们可以让计算器或计算机产生取值于集合{1, 2, 3, 4, 5}的随机数,用1, 2表示红球,用3, 4, 5表示白球. 这样不断产生1~5之间的整数随机数,相当于不断地做从袋中摸球的试验.
随机数与伪随机数
例如我们要产生1~9 之间的随机整数,像彩票摇奖那样,把10个质地和大小相同的号码球放入摇奖器中,充分搅拌后摇出一个球,这个球上的号码就称为随机数.计算器或计算机产生的随机数是按照确定的算法产生的数,具有周期性(周期很长),它们具有类似随机数的性质.因此,计算器或计算机产生的随机数不是真正的随机数,我们称它们为伪随机数.
新知探究
下表数据是用电子表格软件模拟上述摸球试验的结果,其中n为试验次数,nA为摸到红球的频数,fn(A) 为摸到红球的频率.
n 10 20 50 100 150 200 250 300
nA 6 7 20 45 66 77 104 116
fn(A) 0.6 0.35 0.4 0.45 0.44 0.385 0.416 0.39
画出频率折线图如下图所示,从图中可以看出: 随着试验次数的增加,摸到红球的频率稳定于概率0.4.
知新探究
我们称利用随机模拟解决问题的方法为蒙特卡洛(Monte Carlo)方法.
蒙特卡洛方法是在第二次世界大战期间兴起和发展起来的,它的奠基人是冯·诺依曼(John von Neumann).这种方法在应用物理、原子能、固体物理、化学、生物、生态学、社会学以及经济行为等领域中都得到了广泛的应用.
随机模拟方法是通过将一次试验所有可能发生的结果数字化,用计算机或计算器产生的随机数来替代每次试验的结果.
其基本思想是用产生整数随机数的频率估计事件发生的概率.
知新探究
【例3】从你所在班级任意选出6名同学,调查他们的出生月份,假设出生在一月,二月,…,十二月是等可能的.设事件A =“至少有两人出生月份相同”,设计一种试验方法,模拟20次,估计事件A发生的概率.
解:
方法1 根据假设,每个人的出生月份在12个月中是等可能的,而且相互之间没有影响,所以观察6个人的出生月份可以看成可重复试验.
在袋子中装入编号为1,2,…,12的12个球,这些球除编号外没有什么差别.有放回地随机从袋中摸6次球,得到6个数代表6个人的出生月份,这就完成了一次模拟试验.如果这6个数中至少有2个相同,表示事件A发生了.
因此,可以构建如下有放回摸球试验进行模拟:
重复以上模拟试验20次,就可以统计出事件A发生的频率.
知新探究
【例3】从你所在班级任意选出6名同学,调查他们的出生月份,假设出生在一月,二月,…,十二月是等可能的.设事件A =“至少有两人出生月份相同”,设计一种试验方法,模拟20次,估计事件A发生的概率.
解:
方法2 利用电子表格软件模拟试验. 在A1, B1, C1, D1, E1, F1 单元格分别输入“= RANDBETWEEN (1,12)”,得到6个数,代表6个人的出生月份,完成一次模拟试验. 选中Al, Bl, C1, D1, E1, F1单元格,将鼠标指向右下角的黑点,按住鼠标左键拖动到第20行,相当于做20次重复试验. 统计其中有相同数的频率,得到事件A的概率的估计值.
知新探究
随机模拟
上表是20次模拟试验的结果.事件A发生了14次,事件A的概率估计值为0.70,与事件A的概率(约0.78)相差不大.
知新探究
做整数随机模拟试验时应注意的相关事项:
⑴首先要确定随机数的范围,明确哪个数字代表哪个试验结果;
⑵当试验的基本结果的可能性相等时,基本事件总数即为产生随机数的范围,每个随机数代表一个基本事件;
⑶当研究等可能事件的概率时,用按比例分配的方法确定表示各个结果的数字个数及范围;
⑷当每次试验结果需要n个随机数表示时,要把n个随机数作为一组来处理,此时一定要注意每组中的随机数字能否重复.
知新探究
【例4】在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.利用计算机模拟试验,估计甲获得冠军的概率.
解:
分析:奥运会羽毛球比赛规则是3局2胜制,甲获得冠军的结果可能是2:0或2:1.显然,甲连胜2局或在前2局中赢一局输一局,并赢得第3局的概率,与打满3局,甲胜2局或3局的概率相同.每局比赛甲可能胜,也可能负,3局比赛所有可能结果有8种,但是每个结果不是等可能出现的,因此不是古典概型,可以用计算机模拟比赛结果.
由于要比赛3局, 所以每3个随机数为一组. 例如, 产生20组随机数:
设事件A=“甲获得冠军”,事件B=“单局比赛甲胜”,则P(B)=0.6.用计算器或计算机产生1~5之间的随机数,当出现随机数1、2或3时,表示一局比赛甲获胜,其概率为0.6.
423 123 423 344 114 453 525 332 152 342
534 443 512 541 125 432 334 151 314 354.
知新探究
【例4】在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.利用计算机模拟试验,估计甲获得冠军的概率.
解:
423, 123, 423, 114, 332, 152, 342, 512, 125,
432, 334, 151, 314,
相当于做了20次重复试验.其中事件A发生了13次,对应的数组分别是
423 123 423 344 114 453 525 332 152 342
534 443 512 541 125 432 334 151 314 354.
频率估计事件A的概率的近似为=0.65.
用随机模拟的方法得到的是20次试验中事件A发生的频率,事件A的概率的精确值为0.648.
知新探究
【例5】甲、乙两支篮球队进行一次比赛,采用三局两胜制.一局比赛中,甲获胜的概率为0.6,现用随机模拟的方法估计本次比赛乙获胜的概率.先利用计算器或计算机生成0~9之间取整数值的随机数,用0,1,2,3,4,5表示甲获胜,6,7,8,9表示乙获胜.因为采用三局两胜制,所以每3个随机数作为一组.例如,产生30组随机数:
034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959 774 246 762 428 114 572 042 533 237 322 707 360 751
据此估计乙获胜的概率为 .(结果保留到小数点后三位)
解:
如果6,7,8,9中恰有2个或3个数出现,就表示乙获胜,它们分别是738,636,964,736,698,637,616,959,774,762,707,共11个.
这30组数数据就相当于做了30次试验.
所以采用三局两胜制,乙获胜的概率约为0.367.
0.367
初试身手
1.西岳华山是著名的旅游胜地.天气预报称8月1日后连续四天,每天下雨的概率为0.6.现用随机模拟的方法估计四天中恰有三天下雨的概率:在0~9十个整数值中,假定0,1,2,3,4,5表示当天下雨,6,7,8,9表示当天不下雨.在随机数表中从某位置按从左到右的顺序读取如下40组四位随机数:
9533 9522 0018 7472 0018 3879 5869 3281 7890 2692
8280 8425 3990 8460 7980 2436 5987 3882 0753 8935
9635 2379 1805 9890 0735 4640 6298 8054 9720 5695
1574 8008 3216 6470 5080 6772 1642 7920 3189 0343
据此估计四天中恰有三天下雨的概率为( )
A. B. C. D.
在40组四位随机数中,0~5的整数恰好出现3次的四位数有16组,
解:
则四天中恰有三天下雨的概率的估计值为.故选B.
B
初试身手
1.将一枚质地均匀的硬币连掷4次,设事件A =“恰好两次正面朝上”.
⑴直接计算事件A的概率;
⑵利用计算器或计算机模拟试验80次,计算事件A发生的频率.(课本P260 练习 第1题)
⑴P(A)=.
解:
⑵用计算机产生1~2之间的随机数, 当出现随机数为1时表示硬币正面朝上, 当出现随机数为2时表示硬币反面朝上, 然后产生80个数字,计算事件A发生的频率.
课堂小结
1.产生随机数的方法
2.蒙特卡洛方法
利用计算器或计算机软件产生随机数;
构建模拟试验产生随机数.
利用随机模拟解决问题的方法为蒙特卡洛方法.
3.应用随机数估计概率的步骤:
⑴明确随机数的范围及数字与试验结果的对应关系.
⑵产生随机数.
⑶统计试验次数N及所求事件发生的次数n.
⑷计算即可.
作业布置
作业: P260 练习 第2,3题
P261 习题10.3 第2,3,4题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
