2023北京首都师范大学附属苹果园中学初三4月月考数学(PDF版,含解析)
文档属性
| 名称 | 2023北京首都师范大学附属苹果园中学初三4月月考数学(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 905.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-22 18:32:07 | ||
图片预览




文档简介
2023北京首都师大苹中学校初三 4 月月考
数 学
考生须知:
1.本试卷共 8页,28道小题,满分 100分.考试时间 120分钟.
2.在答题卡上准确填写学校名称、姓名和准考证号.
3.试题答案一律填涂或书写在答题卡上,选择题、作图题请用 2B铅笔作答,其他试题请用黑
色字迹签字笔作答,在试卷上作答无效.
4.考试结束,请将本试卷和答题卡一并交回.
一、选择题(每题只有一个正确答案,每题 2分,共 16分)
1. 如图是圆规示意图,张开的两脚所形成的角大约是( )
A. 90° B. 60° C. 45° D. 30°
2. 若 x 1在实数范围内有意义,则实数 x的取值范围是( )
A. x 1 B. x 1 C. x 1 D. x 1
3. 实数 a,b,c 在数轴上的对应点的位置如图所示,若 a = b ,则下列结论中错误的是( )
A. a + b 0 B. a + c 0 C. b + c 0 D. ac 0
4. 若正多边形的内角和是540 ,则该正多边形的一个外角为( )
A. 45 B. 60 C. 72 D. 90
5. 港珠澳大桥是中国第一例集桥、双人工岛、隧道为一体的跨海通道. 其中海底隧道是由 33 个巨型沉管连
接而成,沉管排水总量约 76000 吨. 将数 76000 用科学记数法表示为( )
A. 7.6 104 B. 76 103 C. 0.76 105 D. 7.6 105
a2 +9 2a2
6. 如果 a2 + 3a +1= 0,那么代数式 + 6 的值为( )
a a +3
A. 1 B. 1 C. 2 D. 2
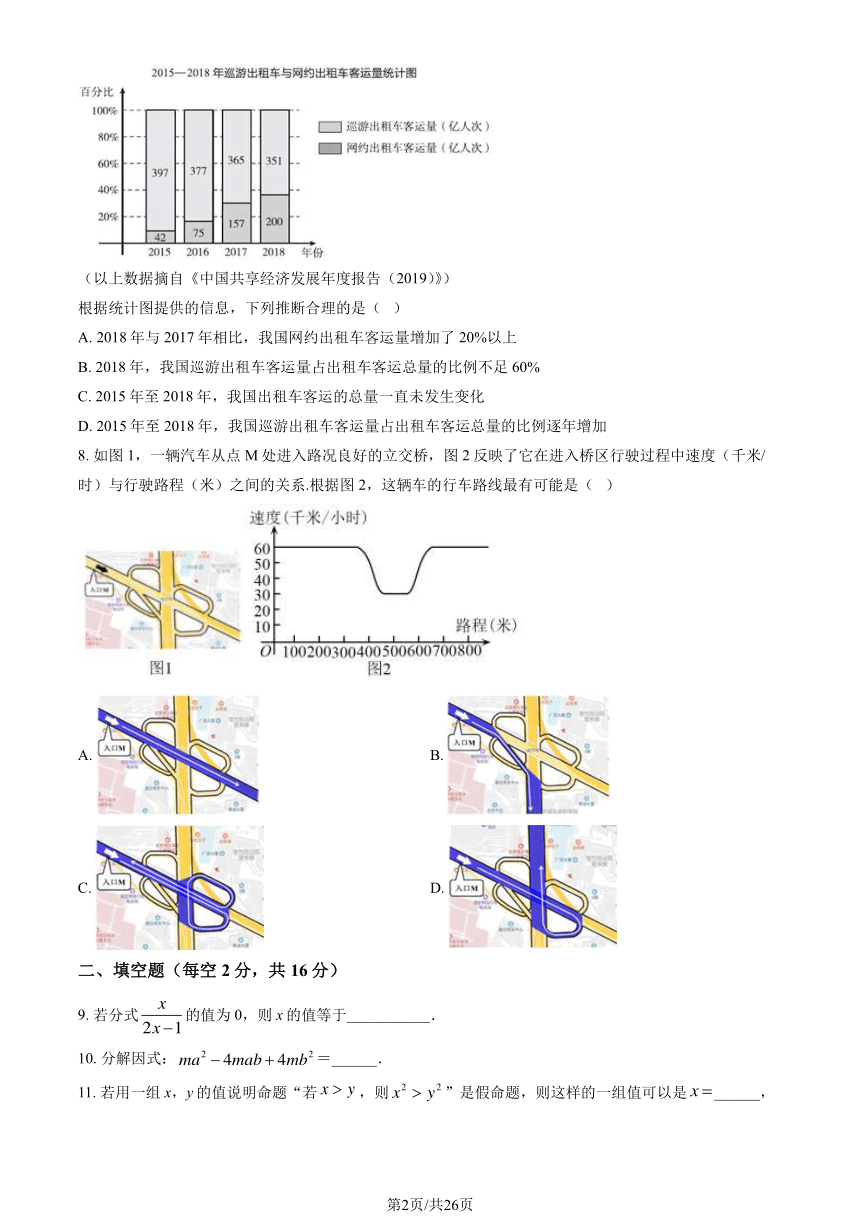
7. 下面的统计图反映了我国出租车(巡游出租车和网约出租车)客运量结构变化.
第1页/共26页
(以上数据摘自《中国共享经济发展年度报告(2019)》)
根据统计图提供的信息,下列推断合理的是( )
A. 2018 年与 2017 年相比,我国网约出租车客运量增加了 20%以上
B. 2018 年,我国巡游出租车客运量占出租车客运总量的比例不足 60%
C. 2015 年至 2018 年,我国出租车客运的总量一直未发生变化
D. 2015 年至 2018 年,我国巡游出租车客运量占出租车客运总量的比例逐年增加
8. 如图 1,一辆汽车从点 M 处进入路况良好的立交桥,图 2 反映了它在进入桥区行驶过程中速度(千米/
时)与行驶路程(米)之间的关系.根据图 2,这辆车的行车路线最有可能是( )
A. B.
C. D.
二、填空题(每空 2分,共 16分)
x
9. 若分式 的值为 0,则 x 的值等于___________.
2x 1
10. 分解因式:ma2 4mab + 4mb2 =______.
11. 若用一组 x,y 的值说明命题“若 x y ,则 x2 y2 ”是假命题,则这样的一组值可以是 x =______,
第2页/共26页
y = ______.
12. 4 月 23 日是世界读书日,甲、乙两位同学在读书日到来之际共购买图书 22 本,其中甲同学购买的图书
数量比乙同学购买的图书数量的 2 倍多 1,求甲、乙两位同学分别购买的图书数量.设甲同学购买图书 x
本、乙同学购买图书 y 本,则可列方程组为___________.
13. 有人做了掷骰子的大量重复试验,统计结果如下表所示:
m
投掷次数(n) “出现点数为 1”的次数(频数 m) 频率
n
300 52 0.173
400 65 0.163
500 80 0.160
600 99 0.165
700 114 0.163
800 136 0.170
900 151 0.168
1000 166 0.166
根据上表信息,掷一枚骰子,估计“出现点数为 1”的概率为__________(精确到 0.001)
14. 如图,矩形 ABCD 中,AB=4,BC=3,DE⊥AC 于点 E,则 AE=__.
2
15. 若关于 x 的一元二次方程 x + 2(m +1)x + c = 0 有两个相等的实数根,则 c 的最小值是___________.
16. 高速公路某收费站出城方向有编号为 A,B,C,D,E的五个小客车收费出口,假定各收费出口每 20分
钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口 20 分钟一共通过的小
客车数量记录如下:
收费出口编号 A,B B,C C,D D,E E,A
通过小客车数量(辆) 260 330 300 360 240
在 A,B,C,D,E 五个收费出口中,每 20 分钟通过小客车数量最多的收费出口的编号是_______.
第3页/共26页
三、解答题(本题共 68分,第 17﹣22题,每小题 5分,第 23﹣26题,每小题 6分,第
27,28题,每小题 7分)解答应写出文字说明、演算步骤或证明过程.
17. 计算: 5 + 12 2sin 60 (2019 )0
4(2x 1) 3x +1
18. 解不等式组: 3x 8
x
5
19. 下面是小东设计的“作圆的一个内接矩形,并使其对角线的夹角为 60°”的尺规作图过程.
已知:⊙O
求作:矩形 ABCD,使得矩形 ABCD 内接于⊙O,且其对角线 AC,BD 的夹角为 60°.
作法:如图
①作⊙O 的直径 AC;
②以点 A 为圆心,AO 长为半径画弧,交直线 AC 上方的圆弧于点 B;
③连接 BO 并延长交⊙O 于点 D;
所以四边形 ABCD 就是所求作的矩形.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵点 A,C 都在⊙O 上,
∴OA=OC
同理 OB=OD
∴四边形 ABCD 是平行四边形
∵AC 是⊙O 的直径,
∴∠ABC=90°( )(填推理的依据)
∴四边形 ABCD 是矩形
∵AB= =BO,
∴四边形 ABCD 四所求作的矩形.
20. 已知关于 x的一元二次方程 x2 + bx + c = 0 .
(1)当 c = b 2时,利用根的判别式判断方程根的情况,
(2)若方程有两个相等的非零实数根,写出一组满足条件的b,c的值,并求此时方程的根.
21. 如图,在△ABC 中,AC=BC,点 D, E, F 分别是 AB,AC, BC 的中点,连接 DE,DF.
第4页/共26页
(1)求证:四边形 DFCE 是菱形;
(2)若∠A=75°,AC=4,求菱形 DFCE 的面积.
m
22. 在平面直角坐标系 xOy 中,一次函数 y = k(x 1) + 6(k 0) 的图象与反比例函数 y = (m≠0)的图象
x
的一个交点的横坐标为 1.
(1)求这个反比例函数的解析式;
m
(2)当 x<﹣3 时,对于 x 的每一个值,反比例函数 y= 的值大于一次函数 y = k(x 1) + 6(k 0) 的值,
x
直接写出 k 的取值范围.
23. 如图,杂技团进行杂技表演,演员要从跷跷板右端 A 处弹跳后恰好落在人梯的顶端 B 处,其身体(看
成一点)的路径是一条抛物线.现测量出如下的数据,设演员身体距起跳点 A 水平距离为 d 米时,距地面
的高度为 h 米.
d(米) … 1.00 1.50 2.00 2.50 3.00 3.50 …
h(米) … 3.40 4.15 4.60 4.75 4.60 4.15 …
请你解决以下问题:
(1)在下边网格中建立适当平面直角坐标系,根据已知数据描点,并用平滑曲线连接;
(2)结合表中所给的数据或所画的图象,直接写出演员身体距离地面的最大高度;
(3)求起跳点 A 距离地面的高度;
(4)在一次表演中,已知人梯到起跳点 A 的水平距离是 3 米,人梯的高度是 3.40 米.问此次表演是否成
第5页/共26页
功?如果成功,说明理由;如果不成功,说明应怎样调节人梯到起跳点 A 的水平距离才能成功?
24. 如图,已知 Rt△ABC 中,∠ACB=90°,E 为 AB 上一点,以 AE 为直径作⊙O 与 BC 相切于点 D,连
接 ED 并延长交 AC 的延长线于点 F.
(1)求证:AE=AF;
(2)若 AE=5,AC=4,求 BE 的长.
25. 某校计划更换校服款式.为调研学生对 A,B 两款校服的满意度,随机抽取了 20 名同学试穿两款校
服,对舒适性、性价比和时尚性进行评分(满分均为 20 分),并按照 1∶1∶1 的比计算综合评分.将数据
(评分)进行整理、描述和分析.下面给出了部分信息.
a.A,B 两款校服各项评分的平均数(精确到 0.1)如下:
款式 舒适性评分平均数 性价比评分平均数 时尚性评分平均数 综合评分平均数
A 19.5 19.6 10.2
B 19.2 18.5 10.4 16.0
b.不同评分对应的满意度如下表:
评分 0≤x<5 5≤x<10 10≤x<15 15≤x≤20
满意度 不满意 基本满意 满意 非常满意
c.A,B 两款校服时尚性满意度人数分布统计图如下:
d.B 校服时尚性评分在 10≤x<15 这一组的是:
10 11 12 12 14
第6页/共26页
根据以上信息,回答下列问题:
(1)在此次调研中,
① A 校服综合评分平均数是否达到“非常满意”: (填“是”或“否”);
② A 校服时尚性满意度达到“非常满意”的人数为 ;
(2)在此次调研中,B 校服时尚性评分的中位数为 ;
(3)在此次调研中,记 A 校服时尚性评分高于其平均数的人数为 m,B 校服时尚性评分高于其平均数的人
数为 n.比较 m,n 的大小,并说明理由.
26. 在平面直角坐标系 xOy 中,点(m – 2, y1),(m, y2),(2- m, y 23)在抛物线 y = x -2ax + 1 上,其中 m≠1
且 m≠2.
(1)直接写出该抛物线的对称轴的表达式(用含 a 的式子表示);
(2)当 m = 0 时,若 y1= y3,比较 y1与 y2的大小关系,并说明理由;
(3)若存在大于 1 的实数 m,使 y1>y2>y3,求 a 的取值范围.
27. 在 ABC 中, AB = AC ,过点 C 作射线CB ,使 ACB = ACB(点 B 与点 B 在直线 AC 的异侧),
点 D 是射线CB 上一个动点(不与点 C 重合),点 E 在线段 BC 上,且 DAE + ACD = 90 .
(1)如图 1,当点 E 与点 C 重合时, AD 与CB 的位置关系是______,若BC = a ,则CD 的长为
______;(用含 a 的式子表示)
(2)如图 2,当点 E 与点 C 不重合时.连接 DE .
①直接写出 BAC 与 DAE 之间的数量关系为__________;
②用等式表示线段 BE ,CD , DE 之间的数量关系,并证明.
2
28. 对于平面直角坐标系 xOy 中的线段 PQ ,给出如下定义:若存在 PQR 使得 S PQR = PQ ,则称
PQR 为线段 PQ 的“等幂三角形”,点 R 称为线段 PQ 的“等幂点”.
(1)已知 A(3,0) .
①在点 P1(1,3), P2(2,6), P3( 5,1), P4(3, 6) 中,是线段OA的“等幂点”的是_____________;
②若存在等腰 OAB是线段OA的“等幂三角形”,求点 B 的坐标;
(2)已知点 C 的坐标为C(2, 1) ,点 D 在直线 y = x 3上,记图形 M 为以点T (1,0) 为圆心,2 为半径
的 T 位于 x 轴上方的部分,若图形 M 上存在点 E,使得线段CD 的“等幂三角形” CDE 为锐角三角
形,直接写出点 D 的横坐标 xD 的取值范围.
第7页/共26页
参考答案
一、选择题(每题只有一个正确答案,每题 2分,共 16分)
1. 【答案】B
【分析】观察图形,直接判断结果.
【详解】解:观察图形,张开的两脚所形成的角大约是60 ,
故选 B.
【点睛】本题考查了角的概念,正确的识别图形是解题的关键.
2.
【分析】根据二次根式有意义的条件求解即可.
【详解】解:由题意得: x 1 0,
解得: x 1,
故选 A.
【点睛】本题考查了二次根式有意义的条件.解题的关键在于熟练掌握二次根式有意义的条件为被开方数
为非负数.
3. 【答案】A
【分析】根据 a = b ,确定原点的位置,根据实数与数轴,有理数的运算法则即可解答.
【详解】解:∵ a = b ,
∴原点在 a,b 的中间,
如图,
由图可得: a c , a + b = 0, a + c 0,b + c 0, ac 0,
故选项 A 错误,
故选 A.
【点睛】本题考查数轴,绝对值,有理数的乘法、加法,解题的关键是确定原点的位置.
4. 【答案】C
【分析】根据多边形的内角和公式 (n 2) 180 求出多边形的边数,再根据多边形的外角和是固定的
360 ,依此可以求出多边形的一个外角.
【详解】 正多边形的内角和是540 ,
多边形的边数为540 180 + 2=5,
多边形的外角和都是360 ,
第8页/共26页
多边形的每个外角=360 5=72 .
故选C .
【点睛】本题主要考查了多边形的内角和与外角和之间的关系,关键是记住内角和的公式与外角和的特
征,难度适中.
5. 【答案】A
【分析】科学记数法的表示形式为 a×10n的形式,其中 1≤|a|<10,n 为整数.确定 n的值时,要看把原数变
成 a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于 10时,n是正数;
当原数的绝对值小于 1 时,n 是负数.
【详解】数据 76000 用科学记数法表示为 7.6×104.
故选 A.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为 a×10n的形式,其中 1≤|a|<10,n 为
整数,表示时关键要正确确定 a 的值以及 n 的值.
6. 【答案】D
【分析】根据分式的加法和乘法可以化简题目中的式子,然后根据 a2+3a+1=0,即可求得所求式子的值.
a2 +9 2a2
【详解】 + 6 ,
a a +3
a2 +9+ 6a 2a2
=
a a +3
2
(a +3) 2a2
=
a a +3
=2a(a+3)
=2(a2+3a),
∵a2+3a+1=0,
∴a2+3a=-1,
∴原式=2×(-1)=-2,
故选 D.
【点睛】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.
7. 【答案】A
【分析】根据统计图中的数据,可以判断各个选项中的说法是否正确,本题得以解决.
200 157
【详解】解:2018年与 2017年相比,我国网约出租车客运量增加了 100% 27.38% ,增加量超过
157
20% ,故选项 A 正确,
2018 年,我国巡游出租车客运量占出租车客运总量的比例超过60% ,故选项 B 错误,
2015 年至 2018 年,我国出租车客运的总量发生了变化,故选项 C 错误,
2015 年至 2018 年,我国巡游出租车客运量占出租车客运总量的比例逐年减少,故选项 D 错误,
第9页/共26页
故选 A.
【点睛】本题考查条形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
8. 【答案】D
【分析】由图 2 可得,行车速度在途中迅速减小并稳定了 100 多米然后又迅速提升,说明应该是进行一次
性的拐弯,再对 4 个选项进行排除选择.
【详解】解: A.行车路线为直线,则速度一直不变,排除;
B.进入辅路后向右转弯,速度减小应该不大,排除;
C.向前行驶然后拐了两次弯再掉头行驶,中间速度应该有两次变大变小的波动呢,排除;
D.向前行驶拐了个较大的弯再进入直路行驶,满足图 2 的速度变化情况.
故选 D.
【点睛】本题考查了函数图象的应用,正确理解函数图象的自变量和函数关系并对照实际问题进行分析是
解题关键.
二、填空题(每空 2分,共 16分)
9. 【答案】0
【分析】分式值为零的条件是分子等于零且分母不等于零.
x
【详解】解∵分式 的值为 0,
2x 1
x = 0
∴ ,
2x 1 0
1
解得 x=0 且 x≠ ,
2
∴x 的值为 0,
故答案为:0.
【点睛】此题主要考查了分式的值为零的条件,注意:“分母不为零”这个条件不能少.
2
10. 【答案】m (a 2b)
【分析】先提公因式,然后用完全平方公式进行因式分解即可.
2 2
【详解】解:原式= m (a 4ab+ 4b )
2
= m (a 2b)
2
故答案为:m (a 2b) .
【点睛】本题考查了综合提公因式与公式法进行因式分解.解题的关键在于正确的运算.
11. 【答案】 ①. 0 ②. -2
【分析】根据 x>y 给出 x、y 值,计算乘方,使 x2【详解】解:若 x=0,y=-2,则满足 x>y 的条件,
∴x2=0,y2=4,
第10页/共26页
∴ 2 2,不符合 x2 2x故答案为:0,-2(答案不唯一).
【点睛】此题考查了有理数的大小比较,假命题的判断,正确理解命题中的题设和结论,对应给出数值是
解题的关键.
x + y = 22
12.【答案】
x = 2y +1
【分析】根据题意分别列出二元一次方程,组成方程组即可.
x + y = 22
【详解】由题意得: ,
x = 2y +1
x + y = 22
故答案为: .
x = 2y +1
【点睛】本题考查列二元一次方程组,理解题意,找准数量关系是解题关键.
13. 【答案】0.166
【分析】利用概率=出现的结果数÷数据总数,代入数据进行求解即可得到答案.
【详解】解:由题目表格知
数据总数=300+400+500+600+700+800+900+1000=5200
出现点数为“1”次数=52+65+80+99+114+136+151+166=863
∴“出现点数为 1”的概率=出现点数为“1”次数÷数据总数=863÷5200≈0.166
故答案为:0.166.
【点睛】本题主要考查了频数与频率之间的关系,解题的关键在于能够熟练掌握相关知识进行求解.
9
14. 【答案】 .
5
【分析】利用矩形的性质得到∠ADC=90°,AD=BC=3,CD=AB=4,利用勾股定理计算出 AC=5,利用面
12
积法计算出 DE= ,然后利用勾股定理计算 AE 的长.
5
【详解】解:∵四边形 ABCD 为矩形,
∴∠ADC=90°,AD=BC=3,CD=AB=4,
在 Rt△ADC 中,AC= 32 + 42 = 5,
1 1
∵ DE AC= AD CD,
2 2
3 4 12
∴DE= = ,
5 5
2
12 9
在 Rt△ADE 中,AE= 32 = .
5 5
第11页/共26页
9
故答案为 .
5
【点睛】本题考查了勾股定理,以及矩形的性质:平行四边形的性质矩形都具有;矩形的四个角都是直
角;邻边垂直;矩形的对角线相等.
15. 【答案】0.
【分析】利用根的判别式列出方程,再确定 c 的最小值即可.
2
【详解】解:∵关于 x 的一元二次方程 x + 2(m +1)x + c = 0 有两个相等的实数根,
∴[2(m +1)]2 4c = 0,
∴ c = (m +1)2 0,
则 c 的最小值是 0,
故答案为:0.
【点睛】本题考查了一元二次方程根的判别式,解题关键是熟练运用一元二次方程根的判别式列出方程,
根据非负数的性质确定最值.
16. 【答案】B
【分析】根据表中数据两两相比较即可得到结论.
【详解】解:∵330 260 = 70,330 300 = 30,360 300 = 60,360 240 =120,260 240 = 20 ,
∴A收费出口通过的数量小于C收费出口通过的数量;D收费出口通过的数量小于B收费出口通过的数量;
E 收费出口通过的数量大于 C 收费出口通过的数量;D收费出口通过的数量大于 A收费出口通过的数量;B
收费出口通过的数量大于 E 收费出口通过的数量;
∴ B E C A, B D A ,
∴每 20 分钟通过小客车数量最多的一个收费出口的编号是 B.
故答案为:B.
【点睛】本题主要考查统计表和不等式的基本性质,正确的理解题意是解题的关键.
三、解答题(本题共 68分,第 17﹣22题,每小题 5分,第 23﹣26题,每小题 6分,第
27,28题,每小题 7分)解答应写出文字说明、演算步骤或证明过程.
17. 【答案】4 + 3.
【分析】原式第一项利用绝对值的代数意义化简,第二项化为最简二次根式,第三项利用利用特殊角的三
角函数值计算,第四项利用零指数幂法则计算,最后进行加减运算即可.
0
【详解】 5 + 12 2sin60 (2019 ) ,
3
= 5+ 2 3 2 1,
2
= 4 + 3.
【点睛】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
18. 【答案】 4 x 1.
第12页/共26页
【分析】分别解出两不等式的解集,再求其公共解.
4(2x 1)<3x +1①
【详解】 3x 8
<x②
5
解不等式①得:x<1,
解不等式②得:x>-4,
所以不等式组的解集为:-4<x<1.
【点睛】此题考查解一元一次不等式组,求不等式组的解集应遵循以下原则:同大取较大,同小取较小,
小大大小中间找,大大小小解不了.
19. 【答案】(1)见解析;(2)直径所对圆周角是直角,AO
【分析】(1)根据要求作图即可得;
(2)根据圆周角定理推论及圆的性质求解可得.
【详解】解:(1)如图所示,矩形 ABCD 即为所求;
(2)证明:∵点 A,C 都在⊙O 上,
∴OA=OC
同理 OB=OD
∴四边形 ABCD 是平行四边形
∵AC 是⊙O 的直径,
∴∠ABC=90°(直径所对圆周角是直角)
∴四边形 ABCD 是矩形
∵AB=AO=BO,
∴四边形 ABCD 即为所求作的矩形,
故答案为:直径所对圆周角是直角,AO.
【点睛】本题主要考查作图-复杂作图,涉及到等边三角形的判定与性质、圆周角定理、矩形的性质与判定
等知识,解题的关键是掌握圆周角定理.
20. 【答案】(1)答案见解析(2)答案见解析.
【分析】(1)计算判别式的值得到△=(b-2)2+4,则可判断△>0,然后根据判别式的意义判断方程根的
情况;
(2)利用方程有两个相等的实数根得到△=b2-4c=0,设 b=2,c=1,方程变形为 x2+2x+1=0,然后解方程即
可.
第13页/共26页
【详解】(1)∵c=b-2,
∴△=b2-4c=b2-4(b-2)=(b-2)2+4,
∵(b-2)2≥0,
∴△=(b-2)2+4>0.
∴△>0,
∴方程有两个不相等的实数根;
(2)∵方程有两个相等的实数根,
∴△=b2-4c=0,
若 b=2,c=1,方程变形为 x2+2x+1=0,解得 x1=x2=-1.
【点睛】本题考查了根的判别式:一元二次方程 ax2+bx+c=0(a≠0)的根与△=b2-4ac 有如下关系:当△>0
时,方程有两个不相等的实数根;当△=0 时,方程有两个相等的实数根;当△<0 时,方程无实数根.
21. 【答案】(1)答案见解析(2)答案见解析.
【分析】(1)根据三角形的中位线的性质和菱形的判定定理即可得到结论;
(2)过 E 作 EG⊥BC 于 G,根据等腰三角形和直角三角形的性质即可得到结论.
【详解】(1)证明:∵点 D,E,F 分别是 AB,AC,BC 的中点,
1 1
∴DE∥CF,DE= BC,DF∥CE,DF= AC,
2 2
∴四边形 DECF 是平行四边形,
∵AC=BC,
∴DE=DF,
∴四边形 DFCE 是菱形;
(2)过 E 作 EG⊥BC 于 G,
∵AC=BC,∠A=75°,
∴∠B=∠A=75°,
∴∠C=30°,
1 1
∴EG= CE= AC=1,
2 2
∴菱形 DFCE 的面积=2×1=2.
【点睛】本题考查了菱形的判定和性质,等腰三角形的性质,三角形的中位线的性质,菱形的面积,熟练
掌握菱形的判定定理是解题的关键.
6
22. 【答案】(1) y =
x
第14页/共26页
(2) k 2
【分析】(1)把交点的横坐标代入一次函数解析式中求出交点的纵坐标,根据交点坐标使用待定系数法即
可求出反比例函数解析式.
6
(2)根据题意确定当 x<﹣3 时,反比例函数 y= 的最小值大于一次函数 y = k(x 1) + 6(k 0) 的最大
x
6
值,根据反比例函数的增减性求出当 x<﹣3 时,反比例函数 y= 的取值范围,根据一次函数的增减性求
x
出当 x<﹣3 时一次函数 y = k(x 1) + 6(k 0) 的取值范围,再据此列出不等式并求解即可.
【小问 1 详解】
解:把 x=1 代入一次函数解析式中得 y = k(1 1) + 6 = 6 .
∴一次函数图象和反比例函数图象的交点是 (1,6).
m
把 (1,6)代入反比例函数解析式中得6 = .
1
∴m=6.
6
∴反比例函数的解析式为 y = .
x
【小问 2 详解】
m
解:∵当 x<﹣3 时,对于 x 的每一个值,反比例函数 y= 的值大于一次函数 y = k(x 1) + 6(k 0) 的值,
x
6
∴当 x<﹣3 时,反比例函数 y= 的最小值大于一次函数 y = k(x 1) + 6(k 0) 的最大值.
x
6
∴把 x=-3 代入反比例函数解析式中得 y = = 2,把 x=-3 代入一次函数 y = k(x 1) + 6中得
3
y = k( 3 1) + 6 = 4k + 6 .
6
∴当 x<﹣3 时,反比例函数 y = 的取值范围是大于-2,且小于 0,一次函数 y = k(x 1) + 6(k 0) 的取值
x
范围是大于 4k + 6 .
∴ 2 4k + 6 .
∴ k 2 .
【点睛】本题考查根据自变量求一次函数的函数值,待定系数法求反比例函数解析式,反比例函数的增减
性,一次函数的增减性,熟练掌握这些知识点是解题关键.
23. 【答案】(1)见解析 (2)4.75 米
(3)1米
(4)不成功;应调节人梯到起跳点A 的水平距离为1米或 4 米才能成功.
【分析】(1)建立直角坐标系,将表格中的点描在坐标系内,再用一条平滑的曲线依次连接;
(2)根据表格中的数据或函数图象分析 h的最大值即可;
第15页/共26页
(3)利用待定系数法求出函数的解析式,令 d = 0 ,求 h;
(4)对比表格中的数据可知 d = 3时 h 3.4 ,故不成功,只需计算当 h = 3.4 时d 的大小,由此可知调节
人梯的方案.
【小问 1 详解】
解:如图所示.
【小问 2 详解】
解:由图可知,演员身体距离地面的最大高度为 4.75 米.
【小问 3 详解】
解:设抛物线的表达式为 h = a(d 2.5)2 + 4.75 (a 0),
将点 (1,3.4) 2代入,得3.4 = a(1 2.5) + 4.75,
解得 a = 0.6 .
2该抛物线为 h = 0.6(d 2.5) + 4.75.
2
当 d = 0 时, h = 0.6(0 2.5) + 4.75 =1.
起跳点A 离地面的高度为1米.
【小问 4 详解】
解:由表格可知,当 d = 3时, h 3.4 ,故不成功.
令 h = 3.4 ,即 0.6(d 2.5)2 + 4.75 = 3.4 ,
解得 d =1或 d = 4 .
应调节人梯到起跳点A 的水平距离为1米或 4 米才能成功.
【点睛】本题考查了二次函数的实际应用,待定系数法求函数解析式,二次函数的作图,解决本题的关键
是掌握二次函数的图象与性质.
5
24. 【答案】(1)证明见解析;(2) .
3
【分析】(1)连接OD,根据切线的性质得到OD⊥BC,根据平行线的判定定理得到OD∥AC,求得∠ODE
=∠F,根据等腰三角形的性质得到∠OED=∠ODE,等量代换得到∠OED=∠F,于是得到结论;
(2)根据相似三角形的判定和性质即可得到结论.
【详解】证明:(1)连接 OD,
第16页/共26页
∵BC 切⊙O 于点 D,
∴OD⊥BC,
∴∠ODC=90°,
又∵∠ACB=90°,
∴OD∥AC,
∴∠ODE=∠F,
∵OE=OD,
∴∠OED=∠ODE,
∴∠OED=∠F,
∴AE=AF;
(2)∵OD∥AC
∴△BOD∽△BAC,
BO OD
∴ = ,
AB AC
∵AE=5,AC=4,
BE + 2.5 2.5
即 = ,
BE + 5 4
5
∴BE= .
3
【点睛】本题考查了切线的性质,平行线的性质,相似三角形的判定和性质,正确的作出辅助线是解题的
关键.
25. 【答案】(1)① 是;② 3
(2)10.5 (3)m n,理由见解析
【分析】(1)①根据列表先求出 A 校服综合评分平均,再结合“非常满意”是15 x 20 来进行计算求
解;
②根据 A 校服时尚性满意度达到“非常满意”所占的百分比为15% ,用 20 乘百分比求解;
(2)根据扇形统计图分别求出 B 校服时尚性评分中不满意、基本满意、满意、非常满意人数,再确定出
中位数所在的位置,最后用中位数的求法来求解;
(3)根据频数分统计表和扇形统计图及中位数来求解.
第17页/共26页
【小问 1 详解】
19.5+19.6+10.2
解:①A 校服综合评分平均数是 16.4 ,
3
而“非常满意”是15 x 20,
所以 A 校服综合评分平均数达到了“非常满意”.
故答案为:是;
②A 校服时尚性满意度达到“非常满意”所占的百分比为15%
所以的人数为:20 15% = 3(人).
故答案为:3;
【小问 2 详解】
解:根据题意可知:B 校服时尚性评分中不满意 20 35%=7 (人),基本满意20 10%=2(人),满意
20 25%=5 (人),非常满意 20 30%=6 (人),
中位数位于 10 和 11 位,正好是 B 校服时尚性评分在 10≤x<15 这一组的是前两位数,
10+11
所以 B 校服时尚性评分的中位数为 =10.5;
2
【小问 3 详解】
解:m n .
理由如下:
A 校服时尚性评分的平均数为 10.2,达到“满意”水平,由扇形图可知,20 人中对 A 校服时尚性评分达到
“满意”和“非常满意”的有 45%,即 9 人,因此 A 校服时尚性评分高于其平均数的人数m 9;B 校服
时尚性评分平均数为 10.4,小于其中位数 10.5,因此结合样本数据,在 20 人中 B 校服时尚性评分高于其
平均数的人数 n =10 .
故m n .
【点睛】本是主要考查了统计表和扇形统计图,平均数和中位数,理解图形,从中获取信息是解答关键.
26. 【答案】(1) x = a
(2) y2 y1,理由见解析
(3)a 的取值范围是 0 a 1
【分析】(1)直接根据对称轴公式求即可;
(2)当m = 0时,这三个点分别为( 2, y1 ),(0, y2 ),(2, y3 ),再结合 y1= y3,即可求出函数解析
式,判断即可;
(3)将(m – 2, y1),(m, y2),(2- m, y 23)代入 y = x -2ax + 1 中,再解不等式即可;
【小问 1 详解】
2a
解: x = = a ;
2
【小问 2 详解】
第18页/共26页
当m = 0时,
这三个点分别为( 2, y1 ),(0, y2 ),(2, y3 ),
∵ y1 = y3 ,
∴ ( 2, y1 )与(2, y3 )关于对称轴对称,
∴ 抛物线的对称轴为 x = 0 ,
即 a = 0 .
2
∴函数解析式为 y = x +1
∴ (0, y2 )为抛物线的顶点.
∵ 抛物线的开口向上,
∴ 当 x = 0 时, y2 为函数 y = x
2 2ax +1的最小值.
∴ y2 y1 .
【小问 3 详解】
将 x = m 2, x =m和 x = 2 m分别代入,得:
2
y1 = (m 2) 2a (m 2) +1,
y 22 = m 2am +1,
2
y3 = (2 m) + 2a (2 m)+1.
则有: y1 y2 = 4(a +1 m),
y2 y3 = 4(a 1)(1 m),
于是 y y y 成立,即为 y y 0和 y2 y1 2 3 1 2 3 0 同时成立,
也即为 a m 1和 (a 1)(1 m) 0同时成立.
① 当 a 0 时,m 1 a 0,
故m 1,不存在大于 1 的实数 m;
② 当 a 1时, a 1 0,
要使 (a 1)(1 m) 0,则m 1,也不存在大于 1 的实数 m;
③ 当 a =1时, (a 1)(1 m) = 0,不符合题意;
④ 0 a 1时,
只需取满足1 m a +1的 m 即可满足前述两个不等式同时成立,
第19页/共26页
即 y1 y2 y3 成立.
综上所述,a 的取值范围是 0 a 1.
【点睛】本题考查二次函数的性质,熟悉二次函数的性质是解题的关键,(3)需要注意分类讨论.
1
27. 【答案】(1)互相垂直; a
2
(2)① BAC = 2 DAE ;②BE =CD + DE ,证明见解析
【分析】(1)根据各角之间的关系得出 DAC + ACD = 90 ,即可确定位置关系;再由全等三角形的
判定和性质得出 ACD≌ ACM (AAS),即可得出结果;
(2)①过点 A 作 AM ⊥ BC 于点M 、 AN ⊥ CB 点 N,根据各角之间的关系及全等三角形的判定得出
CAN≌ ACM (AAS),再由其性质即可得出结果;
②在 BC 上截取 BF = CD ,连接 AF ,由各角之间的关系得出 B = ACB = ACD,再由全等三角
形的判定和性质得出△ABF≌△ACD (SAS), FAE≌ DAE (SAS),即可得出结果.
【小问 1 详解】
解:当点 E 与点 C 重合时,
DAE = DAC ,
∵ DAE + ACD = 90 ,
∴ DAC + ACD = 90 ,
∵ ACD=90 ,
∴ AD ⊥ CB ,
即 AD 与CB 的位置关系是互相垂直,
若 BC = a ,过点 A 作 AM ⊥ BC 于点 M,
如图:
则 AMC = 90 = ACD,
∵ AB = AC ,
1 1
∴CM = BM = BC = a ,
2 2
在 ACD与△ACM 中,
ADC = AMC , ACD = ACM , AC = AC ,
第20页/共26页
∴ ACD≌ ACM (AAS),
1
∴CD =CM = a,
2
1
即CD 的长为 a,
2
1
故答案为:互相垂直; a ;
2
【小问 2 详解】
①当点 E 与点 C 不重合时,用等式表示 BAC 与 DAE 之间的数量关系是: BAC = 2 DAE ,证明
如下:
过点 A 作 AM ⊥ BC 于点 M、 AN ⊥ CB 点 N,如图:
则 AMC + ANC = 90 ,
∴ CAN + ACB = 90 ,
∵ DAE + ACD = 90 ,
即 DAE + ACB = 90 ,
∴ DAE = CAN ,
∵ AB = AC , AM ⊥ BC ,
∴ BAC = 2 CAM = 2 BAM ,
在△ACN 与△ACM 中,
ANC = AMC , ACN = ACM , AC = AC ,
∴ CAN≌ ACM (AAS),
∴ CAN = CAM ,
∴ BAC = 2 CAM = 2 CAN = 2 DAE ;
故答案为: BAC = 2 DAE
②用等式表示线段 BE 、CD 、 DE 之间的数量关系是: BE = CD + DE ,证明如下:
在 BC 上截取 BF = CD ,连接 AF ,如图:
第21页/共26页
∵ AB = AC ,
∴ B = ACB,
∵ ACB = ACB,
∴ B = ACB = ACD,
在△ABF 和 ACD中,
AB = AC , B = ACD , BF = CD ,
∴△ABF≌△ACD (SAS),
∴ AF = AD , BAF = CAD ,
∴ BAF + CAE = CAD + CAE = DAE ,
由①知: BAC = 2 DAE ,
1
即 DAE = BAC ,
2
1
∴ BAF + CAE = BAC ,
2
1
∴ FAE = BAC ( BAF + CAE ) = BAC ,
2
∴ FAE = DAE ,
在 FAE 和 DAE 中,
AF = AD , FAE = DAE , AE = AE ,
∴ FAE≌ DAE (SAS),
∴ FE = DE ,
∴ BE = FE + BF = CD + DE .
【点睛】题目主要考查全等三角形的判定和性质,等腰三角形的性质等,理解题意,作出相应辅助线,熟
练运用全等三角形的判定和性质是解决本题的关键.
3 3 3 2 5+ 2
28. 【答案】(1)①P2 , P4 :② ,6 或 ,-6 ;(2) x 1或D 3 xD
2 2 2 2
【分析】(1)①根据定义求出三角形面积与 OA2进行比较即可确定线段OA的“等幂点”;②如图,由
2
OAB是线段 OA 的“等幂三角形”,可得 S OAB =OA .由点 A 的坐标为 A(3,0),若记 OAB中OA边上
3
的高为 h,可得 S OAB = h = 9, 求出 h = 6 .由 OAB是等腰三角形,点 B 在线段 OA 的垂直平分线上
2
第22页/共26页
3 3
即可求点 B 的坐标为( ,6)或( ,-6);
2 2
(2)设半圆与 x 轴交于 G,H 两点,过 T 作 CH 的平行线与半圆交于 R,作 CH 的垂线交半圆于 Q,直线
y=x-3 与 y 轴交于 N,设 D(x,x-3),过 D 作 y 轴平行线,与过 C 作 x 轴平行线交于 F,求出 N(0,-3),
H(3,0),可证△ONH 为等腰直角三角形,∠OHN=∠ONH=45°,点 D 运动分两种情况,第一种情况点 D
2
在射线 CH,去掉线段 CH 部分运动,在 Rt△TCH 中 TH=2,TC=CH=TH×sin45°=2 = 2 ,QC=2
2
+ 2 ,又因为△ECD 为锐角三角形,点 E 在QR 上运动,点 E 到 CD 的距离 h 的范围是
5+ 2
2 h 2+ 2 ,可求 h=2CD=2 2 (x-2),3 x ; 第二种情况点 D 在射线 CU 上,去掉线段D
2
CU 部分运动,点 E 在QG 上运动,求出 GU=GH×cos45°= 2 2 ,可得 2 2 h 2+ 2 ,可求
3 2
2 2 2 2 (2 x) 2+ 2 ,解不等式即可得 x . D 1
2
1 1 9
【详解】(1)① S OP A = OA yP = 3 3 = OA
2
,P1不是线段 OA 的“等幂点”.
1
2 1 2 2
1 1
S OP A = OA yP = 3 6 = 9=OA
2
, P2是线段 OA 的“等幂点”.
2
2 2 2
1 1 3
S OP A = OA yP = 3 1= OA
2
,P3不是线段 OA 的“等幂点”.
3
2 3 2 2
1 1
S OP A = OA yP = 3 6 = 9 =OA
2
, P4是线段 OA 的“等幂点”.
4
2 4 2
是线段OA的“等幂点”的是 P2 , P4 ,
故答案为: P2 , P4 :
②如图,∵ OAB是线段 OA 的“等幂三角形”,
2
∴ S OAB =OA .
第23页/共26页
∵点 A 的坐标为 A(3,0),若记 OAB中OA边上的高为 h,
1 3
则有 S OAB = OA h = h = 9 .
2 2
解得 h = 6 .
∴点 B 在直线 y = 6或 y = 6上.
∵ OAB是等腰三角形,
∴点 B 在线段 OA 的垂直平分线上.
3 3 3
OA 的垂直平分线为 x= ,与直线 y = 6或 y = 6的交点为 B1( ,6),B2( ,-6),
2 2 2
3 3
综上所述,点 B 的坐标为( ,6)或( ,-6),
2 2
(2)设半圆与 x 轴交于 G,H 两点,过 T 作 CH 的平行线与半圆交于 R,作 CH 的垂线交半圆于 Q,直线
y=x-3 与 y 轴交于 N,
设 D(x,x-3),过 D 作 y 轴平行线,与过 C 作 x 轴平行线交于 F,
当 x=0 时,y=-3,N(0,-3),当 y=0 时,x-3=0,x=3,H(3,0),
∴ON=3=OH,△ONH 为等腰直角三角形,∠OHN=∠ONH=45°,
点 D 运动分两种情况,
第一种情况点 D 在射线 CH,去掉线段 CH 部分运动,
∵TC⊥NH,∠OHN =45°,
∴△TCH 为等腰直角三角形,
2
在 Rt△TCH 中 TH=2,TC=CH=TH×sin45°=2 = 2 ,QC=2 + 2 ,
2
又因为△ECD 为锐角三角形,
第24页/共26页
点 E 在QR 上运动,
点 E 到 CD 的距离 h 的范围是 2 h 2+ 2 ,
CD=CF÷cos45°= 2 CF= 2 (x-2),
∵线段CD 的“等幂三角形”,
1
S△CDE= h CD =CD2,
2
∴h=2CD=2 2 (x-2),
∴ 2 2 2 (x 2) 2+ 2 ,
5 5+ 2
解得 x ,
2 2
点 D 在 H 右侧,x>3,
5+ 2
∴3 x ; D
2
第二种情况点 D 在射线 CU 上,去掉线段 CU 部分运动,点 E 在QG 上运动,
又因为△ECD 为锐角三角形,
GU=GH×cos45°= 2 2 ,
∴ 2 2 h 2+ 2 ,
∵线段CD 的“等幂三角形”,
1
S 2△CDE= h CD =CD ,
2
∴h=2CD=2 2 (2-x),
则 2 2 2 2 (2 x) 2+ 2 ,
第25页/共26页
3 2
解得 x 1, D
2
3 2 5+ 2
D 的横坐标 xD 的取值范围为 xD 1或3 x . D
2 2
【点睛】本题考查新定义问题,仔细阅读新定义,抓住三角形的高为底的二倍,涉及三角形面积,等腰三
角形,等腰直角三角形,线段垂直平分线,一次函数的性质,圆的性质,直线与圆的位置关系,锐角三角
函数,锐角三角形,列双边不等式,解不等式等知识,难度较大,综合较强,熟练掌握多方面知识才是解
题关键.
第26页/共26页
数 学
考生须知:
1.本试卷共 8页,28道小题,满分 100分.考试时间 120分钟.
2.在答题卡上准确填写学校名称、姓名和准考证号.
3.试题答案一律填涂或书写在答题卡上,选择题、作图题请用 2B铅笔作答,其他试题请用黑
色字迹签字笔作答,在试卷上作答无效.
4.考试结束,请将本试卷和答题卡一并交回.
一、选择题(每题只有一个正确答案,每题 2分,共 16分)
1. 如图是圆规示意图,张开的两脚所形成的角大约是( )
A. 90° B. 60° C. 45° D. 30°
2. 若 x 1在实数范围内有意义,则实数 x的取值范围是( )
A. x 1 B. x 1 C. x 1 D. x 1
3. 实数 a,b,c 在数轴上的对应点的位置如图所示,若 a = b ,则下列结论中错误的是( )
A. a + b 0 B. a + c 0 C. b + c 0 D. ac 0
4. 若正多边形的内角和是540 ,则该正多边形的一个外角为( )
A. 45 B. 60 C. 72 D. 90
5. 港珠澳大桥是中国第一例集桥、双人工岛、隧道为一体的跨海通道. 其中海底隧道是由 33 个巨型沉管连
接而成,沉管排水总量约 76000 吨. 将数 76000 用科学记数法表示为( )
A. 7.6 104 B. 76 103 C. 0.76 105 D. 7.6 105
a2 +9 2a2
6. 如果 a2 + 3a +1= 0,那么代数式 + 6 的值为( )
a a +3
A. 1 B. 1 C. 2 D. 2
7. 下面的统计图反映了我国出租车(巡游出租车和网约出租车)客运量结构变化.
第1页/共26页
(以上数据摘自《中国共享经济发展年度报告(2019)》)
根据统计图提供的信息,下列推断合理的是( )
A. 2018 年与 2017 年相比,我国网约出租车客运量增加了 20%以上
B. 2018 年,我国巡游出租车客运量占出租车客运总量的比例不足 60%
C. 2015 年至 2018 年,我国出租车客运的总量一直未发生变化
D. 2015 年至 2018 年,我国巡游出租车客运量占出租车客运总量的比例逐年增加
8. 如图 1,一辆汽车从点 M 处进入路况良好的立交桥,图 2 反映了它在进入桥区行驶过程中速度(千米/
时)与行驶路程(米)之间的关系.根据图 2,这辆车的行车路线最有可能是( )
A. B.
C. D.
二、填空题(每空 2分,共 16分)
x
9. 若分式 的值为 0,则 x 的值等于___________.
2x 1
10. 分解因式:ma2 4mab + 4mb2 =______.
11. 若用一组 x,y 的值说明命题“若 x y ,则 x2 y2 ”是假命题,则这样的一组值可以是 x =______,
第2页/共26页
y = ______.
12. 4 月 23 日是世界读书日,甲、乙两位同学在读书日到来之际共购买图书 22 本,其中甲同学购买的图书
数量比乙同学购买的图书数量的 2 倍多 1,求甲、乙两位同学分别购买的图书数量.设甲同学购买图书 x
本、乙同学购买图书 y 本,则可列方程组为___________.
13. 有人做了掷骰子的大量重复试验,统计结果如下表所示:
m
投掷次数(n) “出现点数为 1”的次数(频数 m) 频率
n
300 52 0.173
400 65 0.163
500 80 0.160
600 99 0.165
700 114 0.163
800 136 0.170
900 151 0.168
1000 166 0.166
根据上表信息,掷一枚骰子,估计“出现点数为 1”的概率为__________(精确到 0.001)
14. 如图,矩形 ABCD 中,AB=4,BC=3,DE⊥AC 于点 E,则 AE=__.
2
15. 若关于 x 的一元二次方程 x + 2(m +1)x + c = 0 有两个相等的实数根,则 c 的最小值是___________.
16. 高速公路某收费站出城方向有编号为 A,B,C,D,E的五个小客车收费出口,假定各收费出口每 20分
钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口 20 分钟一共通过的小
客车数量记录如下:
收费出口编号 A,B B,C C,D D,E E,A
通过小客车数量(辆) 260 330 300 360 240
在 A,B,C,D,E 五个收费出口中,每 20 分钟通过小客车数量最多的收费出口的编号是_______.
第3页/共26页
三、解答题(本题共 68分,第 17﹣22题,每小题 5分,第 23﹣26题,每小题 6分,第
27,28题,每小题 7分)解答应写出文字说明、演算步骤或证明过程.
17. 计算: 5 + 12 2sin 60 (2019 )0
4(2x 1) 3x +1
18. 解不等式组: 3x 8
x
5
19. 下面是小东设计的“作圆的一个内接矩形,并使其对角线的夹角为 60°”的尺规作图过程.
已知:⊙O
求作:矩形 ABCD,使得矩形 ABCD 内接于⊙O,且其对角线 AC,BD 的夹角为 60°.
作法:如图
①作⊙O 的直径 AC;
②以点 A 为圆心,AO 长为半径画弧,交直线 AC 上方的圆弧于点 B;
③连接 BO 并延长交⊙O 于点 D;
所以四边形 ABCD 就是所求作的矩形.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵点 A,C 都在⊙O 上,
∴OA=OC
同理 OB=OD
∴四边形 ABCD 是平行四边形
∵AC 是⊙O 的直径,
∴∠ABC=90°( )(填推理的依据)
∴四边形 ABCD 是矩形
∵AB= =BO,
∴四边形 ABCD 四所求作的矩形.
20. 已知关于 x的一元二次方程 x2 + bx + c = 0 .
(1)当 c = b 2时,利用根的判别式判断方程根的情况,
(2)若方程有两个相等的非零实数根,写出一组满足条件的b,c的值,并求此时方程的根.
21. 如图,在△ABC 中,AC=BC,点 D, E, F 分别是 AB,AC, BC 的中点,连接 DE,DF.
第4页/共26页
(1)求证:四边形 DFCE 是菱形;
(2)若∠A=75°,AC=4,求菱形 DFCE 的面积.
m
22. 在平面直角坐标系 xOy 中,一次函数 y = k(x 1) + 6(k 0) 的图象与反比例函数 y = (m≠0)的图象
x
的一个交点的横坐标为 1.
(1)求这个反比例函数的解析式;
m
(2)当 x<﹣3 时,对于 x 的每一个值,反比例函数 y= 的值大于一次函数 y = k(x 1) + 6(k 0) 的值,
x
直接写出 k 的取值范围.
23. 如图,杂技团进行杂技表演,演员要从跷跷板右端 A 处弹跳后恰好落在人梯的顶端 B 处,其身体(看
成一点)的路径是一条抛物线.现测量出如下的数据,设演员身体距起跳点 A 水平距离为 d 米时,距地面
的高度为 h 米.
d(米) … 1.00 1.50 2.00 2.50 3.00 3.50 …
h(米) … 3.40 4.15 4.60 4.75 4.60 4.15 …
请你解决以下问题:
(1)在下边网格中建立适当平面直角坐标系,根据已知数据描点,并用平滑曲线连接;
(2)结合表中所给的数据或所画的图象,直接写出演员身体距离地面的最大高度;
(3)求起跳点 A 距离地面的高度;
(4)在一次表演中,已知人梯到起跳点 A 的水平距离是 3 米,人梯的高度是 3.40 米.问此次表演是否成
第5页/共26页
功?如果成功,说明理由;如果不成功,说明应怎样调节人梯到起跳点 A 的水平距离才能成功?
24. 如图,已知 Rt△ABC 中,∠ACB=90°,E 为 AB 上一点,以 AE 为直径作⊙O 与 BC 相切于点 D,连
接 ED 并延长交 AC 的延长线于点 F.
(1)求证:AE=AF;
(2)若 AE=5,AC=4,求 BE 的长.
25. 某校计划更换校服款式.为调研学生对 A,B 两款校服的满意度,随机抽取了 20 名同学试穿两款校
服,对舒适性、性价比和时尚性进行评分(满分均为 20 分),并按照 1∶1∶1 的比计算综合评分.将数据
(评分)进行整理、描述和分析.下面给出了部分信息.
a.A,B 两款校服各项评分的平均数(精确到 0.1)如下:
款式 舒适性评分平均数 性价比评分平均数 时尚性评分平均数 综合评分平均数
A 19.5 19.6 10.2
B 19.2 18.5 10.4 16.0
b.不同评分对应的满意度如下表:
评分 0≤x<5 5≤x<10 10≤x<15 15≤x≤20
满意度 不满意 基本满意 满意 非常满意
c.A,B 两款校服时尚性满意度人数分布统计图如下:
d.B 校服时尚性评分在 10≤x<15 这一组的是:
10 11 12 12 14
第6页/共26页
根据以上信息,回答下列问题:
(1)在此次调研中,
① A 校服综合评分平均数是否达到“非常满意”: (填“是”或“否”);
② A 校服时尚性满意度达到“非常满意”的人数为 ;
(2)在此次调研中,B 校服时尚性评分的中位数为 ;
(3)在此次调研中,记 A 校服时尚性评分高于其平均数的人数为 m,B 校服时尚性评分高于其平均数的人
数为 n.比较 m,n 的大小,并说明理由.
26. 在平面直角坐标系 xOy 中,点(m – 2, y1),(m, y2),(2- m, y 23)在抛物线 y = x -2ax + 1 上,其中 m≠1
且 m≠2.
(1)直接写出该抛物线的对称轴的表达式(用含 a 的式子表示);
(2)当 m = 0 时,若 y1= y3,比较 y1与 y2的大小关系,并说明理由;
(3)若存在大于 1 的实数 m,使 y1>y2>y3,求 a 的取值范围.
27. 在 ABC 中, AB = AC ,过点 C 作射线CB ,使 ACB = ACB(点 B 与点 B 在直线 AC 的异侧),
点 D 是射线CB 上一个动点(不与点 C 重合),点 E 在线段 BC 上,且 DAE + ACD = 90 .
(1)如图 1,当点 E 与点 C 重合时, AD 与CB 的位置关系是______,若BC = a ,则CD 的长为
______;(用含 a 的式子表示)
(2)如图 2,当点 E 与点 C 不重合时.连接 DE .
①直接写出 BAC 与 DAE 之间的数量关系为__________;
②用等式表示线段 BE ,CD , DE 之间的数量关系,并证明.
2
28. 对于平面直角坐标系 xOy 中的线段 PQ ,给出如下定义:若存在 PQR 使得 S PQR = PQ ,则称
PQR 为线段 PQ 的“等幂三角形”,点 R 称为线段 PQ 的“等幂点”.
(1)已知 A(3,0) .
①在点 P1(1,3), P2(2,6), P3( 5,1), P4(3, 6) 中,是线段OA的“等幂点”的是_____________;
②若存在等腰 OAB是线段OA的“等幂三角形”,求点 B 的坐标;
(2)已知点 C 的坐标为C(2, 1) ,点 D 在直线 y = x 3上,记图形 M 为以点T (1,0) 为圆心,2 为半径
的 T 位于 x 轴上方的部分,若图形 M 上存在点 E,使得线段CD 的“等幂三角形” CDE 为锐角三角
形,直接写出点 D 的横坐标 xD 的取值范围.
第7页/共26页
参考答案
一、选择题(每题只有一个正确答案,每题 2分,共 16分)
1. 【答案】B
【分析】观察图形,直接判断结果.
【详解】解:观察图形,张开的两脚所形成的角大约是60 ,
故选 B.
【点睛】本题考查了角的概念,正确的识别图形是解题的关键.
2.
【分析】根据二次根式有意义的条件求解即可.
【详解】解:由题意得: x 1 0,
解得: x 1,
故选 A.
【点睛】本题考查了二次根式有意义的条件.解题的关键在于熟练掌握二次根式有意义的条件为被开方数
为非负数.
3. 【答案】A
【分析】根据 a = b ,确定原点的位置,根据实数与数轴,有理数的运算法则即可解答.
【详解】解:∵ a = b ,
∴原点在 a,b 的中间,
如图,
由图可得: a c , a + b = 0, a + c 0,b + c 0, ac 0,
故选项 A 错误,
故选 A.
【点睛】本题考查数轴,绝对值,有理数的乘法、加法,解题的关键是确定原点的位置.
4. 【答案】C
【分析】根据多边形的内角和公式 (n 2) 180 求出多边形的边数,再根据多边形的外角和是固定的
360 ,依此可以求出多边形的一个外角.
【详解】 正多边形的内角和是540 ,
多边形的边数为540 180 + 2=5,
多边形的外角和都是360 ,
第8页/共26页
多边形的每个外角=360 5=72 .
故选C .
【点睛】本题主要考查了多边形的内角和与外角和之间的关系,关键是记住内角和的公式与外角和的特
征,难度适中.
5. 【答案】A
【分析】科学记数法的表示形式为 a×10n的形式,其中 1≤|a|<10,n 为整数.确定 n的值时,要看把原数变
成 a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于 10时,n是正数;
当原数的绝对值小于 1 时,n 是负数.
【详解】数据 76000 用科学记数法表示为 7.6×104.
故选 A.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为 a×10n的形式,其中 1≤|a|<10,n 为
整数,表示时关键要正确确定 a 的值以及 n 的值.
6. 【答案】D
【分析】根据分式的加法和乘法可以化简题目中的式子,然后根据 a2+3a+1=0,即可求得所求式子的值.
a2 +9 2a2
【详解】 + 6 ,
a a +3
a2 +9+ 6a 2a2
=
a a +3
2
(a +3) 2a2
=
a a +3
=2a(a+3)
=2(a2+3a),
∵a2+3a+1=0,
∴a2+3a=-1,
∴原式=2×(-1)=-2,
故选 D.
【点睛】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.
7. 【答案】A
【分析】根据统计图中的数据,可以判断各个选项中的说法是否正确,本题得以解决.
200 157
【详解】解:2018年与 2017年相比,我国网约出租车客运量增加了 100% 27.38% ,增加量超过
157
20% ,故选项 A 正确,
2018 年,我国巡游出租车客运量占出租车客运总量的比例超过60% ,故选项 B 错误,
2015 年至 2018 年,我国出租车客运的总量发生了变化,故选项 C 错误,
2015 年至 2018 年,我国巡游出租车客运量占出租车客运总量的比例逐年减少,故选项 D 错误,
第9页/共26页
故选 A.
【点睛】本题考查条形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
8. 【答案】D
【分析】由图 2 可得,行车速度在途中迅速减小并稳定了 100 多米然后又迅速提升,说明应该是进行一次
性的拐弯,再对 4 个选项进行排除选择.
【详解】解: A.行车路线为直线,则速度一直不变,排除;
B.进入辅路后向右转弯,速度减小应该不大,排除;
C.向前行驶然后拐了两次弯再掉头行驶,中间速度应该有两次变大变小的波动呢,排除;
D.向前行驶拐了个较大的弯再进入直路行驶,满足图 2 的速度变化情况.
故选 D.
【点睛】本题考查了函数图象的应用,正确理解函数图象的自变量和函数关系并对照实际问题进行分析是
解题关键.
二、填空题(每空 2分,共 16分)
9. 【答案】0
【分析】分式值为零的条件是分子等于零且分母不等于零.
x
【详解】解∵分式 的值为 0,
2x 1
x = 0
∴ ,
2x 1 0
1
解得 x=0 且 x≠ ,
2
∴x 的值为 0,
故答案为:0.
【点睛】此题主要考查了分式的值为零的条件,注意:“分母不为零”这个条件不能少.
2
10. 【答案】m (a 2b)
【分析】先提公因式,然后用完全平方公式进行因式分解即可.
2 2
【详解】解:原式= m (a 4ab+ 4b )
2
= m (a 2b)
2
故答案为:m (a 2b) .
【点睛】本题考查了综合提公因式与公式法进行因式分解.解题的关键在于正确的运算.
11. 【答案】 ①. 0 ②. -2
【分析】根据 x>y 给出 x、y 值,计算乘方,使 x2
∴x2=0,y2=4,
第10页/共26页
∴ 2 2,不符合 x2 2x
【点睛】此题考查了有理数的大小比较,假命题的判断,正确理解命题中的题设和结论,对应给出数值是
解题的关键.
x + y = 22
12.【答案】
x = 2y +1
【分析】根据题意分别列出二元一次方程,组成方程组即可.
x + y = 22
【详解】由题意得: ,
x = 2y +1
x + y = 22
故答案为: .
x = 2y +1
【点睛】本题考查列二元一次方程组,理解题意,找准数量关系是解题关键.
13. 【答案】0.166
【分析】利用概率=出现的结果数÷数据总数,代入数据进行求解即可得到答案.
【详解】解:由题目表格知
数据总数=300+400+500+600+700+800+900+1000=5200
出现点数为“1”次数=52+65+80+99+114+136+151+166=863
∴“出现点数为 1”的概率=出现点数为“1”次数÷数据总数=863÷5200≈0.166
故答案为:0.166.
【点睛】本题主要考查了频数与频率之间的关系,解题的关键在于能够熟练掌握相关知识进行求解.
9
14. 【答案】 .
5
【分析】利用矩形的性质得到∠ADC=90°,AD=BC=3,CD=AB=4,利用勾股定理计算出 AC=5,利用面
12
积法计算出 DE= ,然后利用勾股定理计算 AE 的长.
5
【详解】解:∵四边形 ABCD 为矩形,
∴∠ADC=90°,AD=BC=3,CD=AB=4,
在 Rt△ADC 中,AC= 32 + 42 = 5,
1 1
∵ DE AC= AD CD,
2 2
3 4 12
∴DE= = ,
5 5
2
12 9
在 Rt△ADE 中,AE= 32 = .
5 5
第11页/共26页
9
故答案为 .
5
【点睛】本题考查了勾股定理,以及矩形的性质:平行四边形的性质矩形都具有;矩形的四个角都是直
角;邻边垂直;矩形的对角线相等.
15. 【答案】0.
【分析】利用根的判别式列出方程,再确定 c 的最小值即可.
2
【详解】解:∵关于 x 的一元二次方程 x + 2(m +1)x + c = 0 有两个相等的实数根,
∴[2(m +1)]2 4c = 0,
∴ c = (m +1)2 0,
则 c 的最小值是 0,
故答案为:0.
【点睛】本题考查了一元二次方程根的判别式,解题关键是熟练运用一元二次方程根的判别式列出方程,
根据非负数的性质确定最值.
16. 【答案】B
【分析】根据表中数据两两相比较即可得到结论.
【详解】解:∵330 260 = 70,330 300 = 30,360 300 = 60,360 240 =120,260 240 = 20 ,
∴A收费出口通过的数量小于C收费出口通过的数量;D收费出口通过的数量小于B收费出口通过的数量;
E 收费出口通过的数量大于 C 收费出口通过的数量;D收费出口通过的数量大于 A收费出口通过的数量;B
收费出口通过的数量大于 E 收费出口通过的数量;
∴ B E C A, B D A ,
∴每 20 分钟通过小客车数量最多的一个收费出口的编号是 B.
故答案为:B.
【点睛】本题主要考查统计表和不等式的基本性质,正确的理解题意是解题的关键.
三、解答题(本题共 68分,第 17﹣22题,每小题 5分,第 23﹣26题,每小题 6分,第
27,28题,每小题 7分)解答应写出文字说明、演算步骤或证明过程.
17. 【答案】4 + 3.
【分析】原式第一项利用绝对值的代数意义化简,第二项化为最简二次根式,第三项利用利用特殊角的三
角函数值计算,第四项利用零指数幂法则计算,最后进行加减运算即可.
0
【详解】 5 + 12 2sin60 (2019 ) ,
3
= 5+ 2 3 2 1,
2
= 4 + 3.
【点睛】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
18. 【答案】 4 x 1.
第12页/共26页
【分析】分别解出两不等式的解集,再求其公共解.
4(2x 1)<3x +1①
【详解】 3x 8
<x②
5
解不等式①得:x<1,
解不等式②得:x>-4,
所以不等式组的解集为:-4<x<1.
【点睛】此题考查解一元一次不等式组,求不等式组的解集应遵循以下原则:同大取较大,同小取较小,
小大大小中间找,大大小小解不了.
19. 【答案】(1)见解析;(2)直径所对圆周角是直角,AO
【分析】(1)根据要求作图即可得;
(2)根据圆周角定理推论及圆的性质求解可得.
【详解】解:(1)如图所示,矩形 ABCD 即为所求;
(2)证明:∵点 A,C 都在⊙O 上,
∴OA=OC
同理 OB=OD
∴四边形 ABCD 是平行四边形
∵AC 是⊙O 的直径,
∴∠ABC=90°(直径所对圆周角是直角)
∴四边形 ABCD 是矩形
∵AB=AO=BO,
∴四边形 ABCD 即为所求作的矩形,
故答案为:直径所对圆周角是直角,AO.
【点睛】本题主要考查作图-复杂作图,涉及到等边三角形的判定与性质、圆周角定理、矩形的性质与判定
等知识,解题的关键是掌握圆周角定理.
20. 【答案】(1)答案见解析(2)答案见解析.
【分析】(1)计算判别式的值得到△=(b-2)2+4,则可判断△>0,然后根据判别式的意义判断方程根的
情况;
(2)利用方程有两个相等的实数根得到△=b2-4c=0,设 b=2,c=1,方程变形为 x2+2x+1=0,然后解方程即
可.
第13页/共26页
【详解】(1)∵c=b-2,
∴△=b2-4c=b2-4(b-2)=(b-2)2+4,
∵(b-2)2≥0,
∴△=(b-2)2+4>0.
∴△>0,
∴方程有两个不相等的实数根;
(2)∵方程有两个相等的实数根,
∴△=b2-4c=0,
若 b=2,c=1,方程变形为 x2+2x+1=0,解得 x1=x2=-1.
【点睛】本题考查了根的判别式:一元二次方程 ax2+bx+c=0(a≠0)的根与△=b2-4ac 有如下关系:当△>0
时,方程有两个不相等的实数根;当△=0 时,方程有两个相等的实数根;当△<0 时,方程无实数根.
21. 【答案】(1)答案见解析(2)答案见解析.
【分析】(1)根据三角形的中位线的性质和菱形的判定定理即可得到结论;
(2)过 E 作 EG⊥BC 于 G,根据等腰三角形和直角三角形的性质即可得到结论.
【详解】(1)证明:∵点 D,E,F 分别是 AB,AC,BC 的中点,
1 1
∴DE∥CF,DE= BC,DF∥CE,DF= AC,
2 2
∴四边形 DECF 是平行四边形,
∵AC=BC,
∴DE=DF,
∴四边形 DFCE 是菱形;
(2)过 E 作 EG⊥BC 于 G,
∵AC=BC,∠A=75°,
∴∠B=∠A=75°,
∴∠C=30°,
1 1
∴EG= CE= AC=1,
2 2
∴菱形 DFCE 的面积=2×1=2.
【点睛】本题考查了菱形的判定和性质,等腰三角形的性质,三角形的中位线的性质,菱形的面积,熟练
掌握菱形的判定定理是解题的关键.
6
22. 【答案】(1) y =
x
第14页/共26页
(2) k 2
【分析】(1)把交点的横坐标代入一次函数解析式中求出交点的纵坐标,根据交点坐标使用待定系数法即
可求出反比例函数解析式.
6
(2)根据题意确定当 x<﹣3 时,反比例函数 y= 的最小值大于一次函数 y = k(x 1) + 6(k 0) 的最大
x
6
值,根据反比例函数的增减性求出当 x<﹣3 时,反比例函数 y= 的取值范围,根据一次函数的增减性求
x
出当 x<﹣3 时一次函数 y = k(x 1) + 6(k 0) 的取值范围,再据此列出不等式并求解即可.
【小问 1 详解】
解:把 x=1 代入一次函数解析式中得 y = k(1 1) + 6 = 6 .
∴一次函数图象和反比例函数图象的交点是 (1,6).
m
把 (1,6)代入反比例函数解析式中得6 = .
1
∴m=6.
6
∴反比例函数的解析式为 y = .
x
【小问 2 详解】
m
解:∵当 x<﹣3 时,对于 x 的每一个值,反比例函数 y= 的值大于一次函数 y = k(x 1) + 6(k 0) 的值,
x
6
∴当 x<﹣3 时,反比例函数 y= 的最小值大于一次函数 y = k(x 1) + 6(k 0) 的最大值.
x
6
∴把 x=-3 代入反比例函数解析式中得 y = = 2,把 x=-3 代入一次函数 y = k(x 1) + 6中得
3
y = k( 3 1) + 6 = 4k + 6 .
6
∴当 x<﹣3 时,反比例函数 y = 的取值范围是大于-2,且小于 0,一次函数 y = k(x 1) + 6(k 0) 的取值
x
范围是大于 4k + 6 .
∴ 2 4k + 6 .
∴ k 2 .
【点睛】本题考查根据自变量求一次函数的函数值,待定系数法求反比例函数解析式,反比例函数的增减
性,一次函数的增减性,熟练掌握这些知识点是解题关键.
23. 【答案】(1)见解析 (2)4.75 米
(3)1米
(4)不成功;应调节人梯到起跳点A 的水平距离为1米或 4 米才能成功.
【分析】(1)建立直角坐标系,将表格中的点描在坐标系内,再用一条平滑的曲线依次连接;
(2)根据表格中的数据或函数图象分析 h的最大值即可;
第15页/共26页
(3)利用待定系数法求出函数的解析式,令 d = 0 ,求 h;
(4)对比表格中的数据可知 d = 3时 h 3.4 ,故不成功,只需计算当 h = 3.4 时d 的大小,由此可知调节
人梯的方案.
【小问 1 详解】
解:如图所示.
【小问 2 详解】
解:由图可知,演员身体距离地面的最大高度为 4.75 米.
【小问 3 详解】
解:设抛物线的表达式为 h = a(d 2.5)2 + 4.75 (a 0),
将点 (1,3.4) 2代入,得3.4 = a(1 2.5) + 4.75,
解得 a = 0.6 .
2该抛物线为 h = 0.6(d 2.5) + 4.75.
2
当 d = 0 时, h = 0.6(0 2.5) + 4.75 =1.
起跳点A 离地面的高度为1米.
【小问 4 详解】
解:由表格可知,当 d = 3时, h 3.4 ,故不成功.
令 h = 3.4 ,即 0.6(d 2.5)2 + 4.75 = 3.4 ,
解得 d =1或 d = 4 .
应调节人梯到起跳点A 的水平距离为1米或 4 米才能成功.
【点睛】本题考查了二次函数的实际应用,待定系数法求函数解析式,二次函数的作图,解决本题的关键
是掌握二次函数的图象与性质.
5
24. 【答案】(1)证明见解析;(2) .
3
【分析】(1)连接OD,根据切线的性质得到OD⊥BC,根据平行线的判定定理得到OD∥AC,求得∠ODE
=∠F,根据等腰三角形的性质得到∠OED=∠ODE,等量代换得到∠OED=∠F,于是得到结论;
(2)根据相似三角形的判定和性质即可得到结论.
【详解】证明:(1)连接 OD,
第16页/共26页
∵BC 切⊙O 于点 D,
∴OD⊥BC,
∴∠ODC=90°,
又∵∠ACB=90°,
∴OD∥AC,
∴∠ODE=∠F,
∵OE=OD,
∴∠OED=∠ODE,
∴∠OED=∠F,
∴AE=AF;
(2)∵OD∥AC
∴△BOD∽△BAC,
BO OD
∴ = ,
AB AC
∵AE=5,AC=4,
BE + 2.5 2.5
即 = ,
BE + 5 4
5
∴BE= .
3
【点睛】本题考查了切线的性质,平行线的性质,相似三角形的判定和性质,正确的作出辅助线是解题的
关键.
25. 【答案】(1)① 是;② 3
(2)10.5 (3)m n,理由见解析
【分析】(1)①根据列表先求出 A 校服综合评分平均,再结合“非常满意”是15 x 20 来进行计算求
解;
②根据 A 校服时尚性满意度达到“非常满意”所占的百分比为15% ,用 20 乘百分比求解;
(2)根据扇形统计图分别求出 B 校服时尚性评分中不满意、基本满意、满意、非常满意人数,再确定出
中位数所在的位置,最后用中位数的求法来求解;
(3)根据频数分统计表和扇形统计图及中位数来求解.
第17页/共26页
【小问 1 详解】
19.5+19.6+10.2
解:①A 校服综合评分平均数是 16.4 ,
3
而“非常满意”是15 x 20,
所以 A 校服综合评分平均数达到了“非常满意”.
故答案为:是;
②A 校服时尚性满意度达到“非常满意”所占的百分比为15%
所以的人数为:20 15% = 3(人).
故答案为:3;
【小问 2 详解】
解:根据题意可知:B 校服时尚性评分中不满意 20 35%=7 (人),基本满意20 10%=2(人),满意
20 25%=5 (人),非常满意 20 30%=6 (人),
中位数位于 10 和 11 位,正好是 B 校服时尚性评分在 10≤x<15 这一组的是前两位数,
10+11
所以 B 校服时尚性评分的中位数为 =10.5;
2
【小问 3 详解】
解:m n .
理由如下:
A 校服时尚性评分的平均数为 10.2,达到“满意”水平,由扇形图可知,20 人中对 A 校服时尚性评分达到
“满意”和“非常满意”的有 45%,即 9 人,因此 A 校服时尚性评分高于其平均数的人数m 9;B 校服
时尚性评分平均数为 10.4,小于其中位数 10.5,因此结合样本数据,在 20 人中 B 校服时尚性评分高于其
平均数的人数 n =10 .
故m n .
【点睛】本是主要考查了统计表和扇形统计图,平均数和中位数,理解图形,从中获取信息是解答关键.
26. 【答案】(1) x = a
(2) y2 y1,理由见解析
(3)a 的取值范围是 0 a 1
【分析】(1)直接根据对称轴公式求即可;
(2)当m = 0时,这三个点分别为( 2, y1 ),(0, y2 ),(2, y3 ),再结合 y1= y3,即可求出函数解析
式,判断即可;
(3)将(m – 2, y1),(m, y2),(2- m, y 23)代入 y = x -2ax + 1 中,再解不等式即可;
【小问 1 详解】
2a
解: x = = a ;
2
【小问 2 详解】
第18页/共26页
当m = 0时,
这三个点分别为( 2, y1 ),(0, y2 ),(2, y3 ),
∵ y1 = y3 ,
∴ ( 2, y1 )与(2, y3 )关于对称轴对称,
∴ 抛物线的对称轴为 x = 0 ,
即 a = 0 .
2
∴函数解析式为 y = x +1
∴ (0, y2 )为抛物线的顶点.
∵ 抛物线的开口向上,
∴ 当 x = 0 时, y2 为函数 y = x
2 2ax +1的最小值.
∴ y2 y1 .
【小问 3 详解】
将 x = m 2, x =m和 x = 2 m分别代入,得:
2
y1 = (m 2) 2a (m 2) +1,
y 22 = m 2am +1,
2
y3 = (2 m) + 2a (2 m)+1.
则有: y1 y2 = 4(a +1 m),
y2 y3 = 4(a 1)(1 m),
于是 y y y 成立,即为 y y 0和 y2 y1 2 3 1 2 3 0 同时成立,
也即为 a m 1和 (a 1)(1 m) 0同时成立.
① 当 a 0 时,m 1 a 0,
故m 1,不存在大于 1 的实数 m;
② 当 a 1时, a 1 0,
要使 (a 1)(1 m) 0,则m 1,也不存在大于 1 的实数 m;
③ 当 a =1时, (a 1)(1 m) = 0,不符合题意;
④ 0 a 1时,
只需取满足1 m a +1的 m 即可满足前述两个不等式同时成立,
第19页/共26页
即 y1 y2 y3 成立.
综上所述,a 的取值范围是 0 a 1.
【点睛】本题考查二次函数的性质,熟悉二次函数的性质是解题的关键,(3)需要注意分类讨论.
1
27. 【答案】(1)互相垂直; a
2
(2)① BAC = 2 DAE ;②BE =CD + DE ,证明见解析
【分析】(1)根据各角之间的关系得出 DAC + ACD = 90 ,即可确定位置关系;再由全等三角形的
判定和性质得出 ACD≌ ACM (AAS),即可得出结果;
(2)①过点 A 作 AM ⊥ BC 于点M 、 AN ⊥ CB 点 N,根据各角之间的关系及全等三角形的判定得出
CAN≌ ACM (AAS),再由其性质即可得出结果;
②在 BC 上截取 BF = CD ,连接 AF ,由各角之间的关系得出 B = ACB = ACD,再由全等三角
形的判定和性质得出△ABF≌△ACD (SAS), FAE≌ DAE (SAS),即可得出结果.
【小问 1 详解】
解:当点 E 与点 C 重合时,
DAE = DAC ,
∵ DAE + ACD = 90 ,
∴ DAC + ACD = 90 ,
∵ ACD=90 ,
∴ AD ⊥ CB ,
即 AD 与CB 的位置关系是互相垂直,
若 BC = a ,过点 A 作 AM ⊥ BC 于点 M,
如图:
则 AMC = 90 = ACD,
∵ AB = AC ,
1 1
∴CM = BM = BC = a ,
2 2
在 ACD与△ACM 中,
ADC = AMC , ACD = ACM , AC = AC ,
第20页/共26页
∴ ACD≌ ACM (AAS),
1
∴CD =CM = a,
2
1
即CD 的长为 a,
2
1
故答案为:互相垂直; a ;
2
【小问 2 详解】
①当点 E 与点 C 不重合时,用等式表示 BAC 与 DAE 之间的数量关系是: BAC = 2 DAE ,证明
如下:
过点 A 作 AM ⊥ BC 于点 M、 AN ⊥ CB 点 N,如图:
则 AMC + ANC = 90 ,
∴ CAN + ACB = 90 ,
∵ DAE + ACD = 90 ,
即 DAE + ACB = 90 ,
∴ DAE = CAN ,
∵ AB = AC , AM ⊥ BC ,
∴ BAC = 2 CAM = 2 BAM ,
在△ACN 与△ACM 中,
ANC = AMC , ACN = ACM , AC = AC ,
∴ CAN≌ ACM (AAS),
∴ CAN = CAM ,
∴ BAC = 2 CAM = 2 CAN = 2 DAE ;
故答案为: BAC = 2 DAE
②用等式表示线段 BE 、CD 、 DE 之间的数量关系是: BE = CD + DE ,证明如下:
在 BC 上截取 BF = CD ,连接 AF ,如图:
第21页/共26页
∵ AB = AC ,
∴ B = ACB,
∵ ACB = ACB,
∴ B = ACB = ACD,
在△ABF 和 ACD中,
AB = AC , B = ACD , BF = CD ,
∴△ABF≌△ACD (SAS),
∴ AF = AD , BAF = CAD ,
∴ BAF + CAE = CAD + CAE = DAE ,
由①知: BAC = 2 DAE ,
1
即 DAE = BAC ,
2
1
∴ BAF + CAE = BAC ,
2
1
∴ FAE = BAC ( BAF + CAE ) = BAC ,
2
∴ FAE = DAE ,
在 FAE 和 DAE 中,
AF = AD , FAE = DAE , AE = AE ,
∴ FAE≌ DAE (SAS),
∴ FE = DE ,
∴ BE = FE + BF = CD + DE .
【点睛】题目主要考查全等三角形的判定和性质,等腰三角形的性质等,理解题意,作出相应辅助线,熟
练运用全等三角形的判定和性质是解决本题的关键.
3 3 3 2 5+ 2
28. 【答案】(1)①P2 , P4 :② ,6 或 ,-6 ;(2) x 1或D 3 xD
2 2 2 2
【分析】(1)①根据定义求出三角形面积与 OA2进行比较即可确定线段OA的“等幂点”;②如图,由
2
OAB是线段 OA 的“等幂三角形”,可得 S OAB =OA .由点 A 的坐标为 A(3,0),若记 OAB中OA边上
3
的高为 h,可得 S OAB = h = 9, 求出 h = 6 .由 OAB是等腰三角形,点 B 在线段 OA 的垂直平分线上
2
第22页/共26页
3 3
即可求点 B 的坐标为( ,6)或( ,-6);
2 2
(2)设半圆与 x 轴交于 G,H 两点,过 T 作 CH 的平行线与半圆交于 R,作 CH 的垂线交半圆于 Q,直线
y=x-3 与 y 轴交于 N,设 D(x,x-3),过 D 作 y 轴平行线,与过 C 作 x 轴平行线交于 F,求出 N(0,-3),
H(3,0),可证△ONH 为等腰直角三角形,∠OHN=∠ONH=45°,点 D 运动分两种情况,第一种情况点 D
2
在射线 CH,去掉线段 CH 部分运动,在 Rt△TCH 中 TH=2,TC=CH=TH×sin45°=2 = 2 ,QC=2
2
+ 2 ,又因为△ECD 为锐角三角形,点 E 在QR 上运动,点 E 到 CD 的距离 h 的范围是
5+ 2
2 h 2+ 2 ,可求 h=2CD=2 2 (x-2),3 x ; 第二种情况点 D 在射线 CU 上,去掉线段D
2
CU 部分运动,点 E 在QG 上运动,求出 GU=GH×cos45°= 2 2 ,可得 2 2 h 2+ 2 ,可求
3 2
2 2 2 2 (2 x) 2+ 2 ,解不等式即可得 x . D 1
2
1 1 9
【详解】(1)① S OP A = OA yP = 3 3 = OA
2
,P1不是线段 OA 的“等幂点”.
1
2 1 2 2
1 1
S OP A = OA yP = 3 6 = 9=OA
2
, P2是线段 OA 的“等幂点”.
2
2 2 2
1 1 3
S OP A = OA yP = 3 1= OA
2
,P3不是线段 OA 的“等幂点”.
3
2 3 2 2
1 1
S OP A = OA yP = 3 6 = 9 =OA
2
, P4是线段 OA 的“等幂点”.
4
2 4 2
是线段OA的“等幂点”的是 P2 , P4 ,
故答案为: P2 , P4 :
②如图,∵ OAB是线段 OA 的“等幂三角形”,
2
∴ S OAB =OA .
第23页/共26页
∵点 A 的坐标为 A(3,0),若记 OAB中OA边上的高为 h,
1 3
则有 S OAB = OA h = h = 9 .
2 2
解得 h = 6 .
∴点 B 在直线 y = 6或 y = 6上.
∵ OAB是等腰三角形,
∴点 B 在线段 OA 的垂直平分线上.
3 3 3
OA 的垂直平分线为 x= ,与直线 y = 6或 y = 6的交点为 B1( ,6),B2( ,-6),
2 2 2
3 3
综上所述,点 B 的坐标为( ,6)或( ,-6),
2 2
(2)设半圆与 x 轴交于 G,H 两点,过 T 作 CH 的平行线与半圆交于 R,作 CH 的垂线交半圆于 Q,直线
y=x-3 与 y 轴交于 N,
设 D(x,x-3),过 D 作 y 轴平行线,与过 C 作 x 轴平行线交于 F,
当 x=0 时,y=-3,N(0,-3),当 y=0 时,x-3=0,x=3,H(3,0),
∴ON=3=OH,△ONH 为等腰直角三角形,∠OHN=∠ONH=45°,
点 D 运动分两种情况,
第一种情况点 D 在射线 CH,去掉线段 CH 部分运动,
∵TC⊥NH,∠OHN =45°,
∴△TCH 为等腰直角三角形,
2
在 Rt△TCH 中 TH=2,TC=CH=TH×sin45°=2 = 2 ,QC=2 + 2 ,
2
又因为△ECD 为锐角三角形,
第24页/共26页
点 E 在QR 上运动,
点 E 到 CD 的距离 h 的范围是 2 h 2+ 2 ,
CD=CF÷cos45°= 2 CF= 2 (x-2),
∵线段CD 的“等幂三角形”,
1
S△CDE= h CD =CD2,
2
∴h=2CD=2 2 (x-2),
∴ 2 2 2 (x 2) 2+ 2 ,
5 5+ 2
解得 x ,
2 2
点 D 在 H 右侧,x>3,
5+ 2
∴3 x ; D
2
第二种情况点 D 在射线 CU 上,去掉线段 CU 部分运动,点 E 在QG 上运动,
又因为△ECD 为锐角三角形,
GU=GH×cos45°= 2 2 ,
∴ 2 2 h 2+ 2 ,
∵线段CD 的“等幂三角形”,
1
S 2△CDE= h CD =CD ,
2
∴h=2CD=2 2 (2-x),
则 2 2 2 2 (2 x) 2+ 2 ,
第25页/共26页
3 2
解得 x 1, D
2
3 2 5+ 2
D 的横坐标 xD 的取值范围为 xD 1或3 x . D
2 2
【点睛】本题考查新定义问题,仔细阅读新定义,抓住三角形的高为底的二倍,涉及三角形面积,等腰三
角形,等腰直角三角形,线段垂直平分线,一次函数的性质,圆的性质,直线与圆的位置关系,锐角三角
函数,锐角三角形,列双边不等式,解不等式等知识,难度较大,综合较强,熟练掌握多方面知识才是解
题关键.
第26页/共26页
同课章节目录
