1.2.1 任意角的三角函数
图片预览

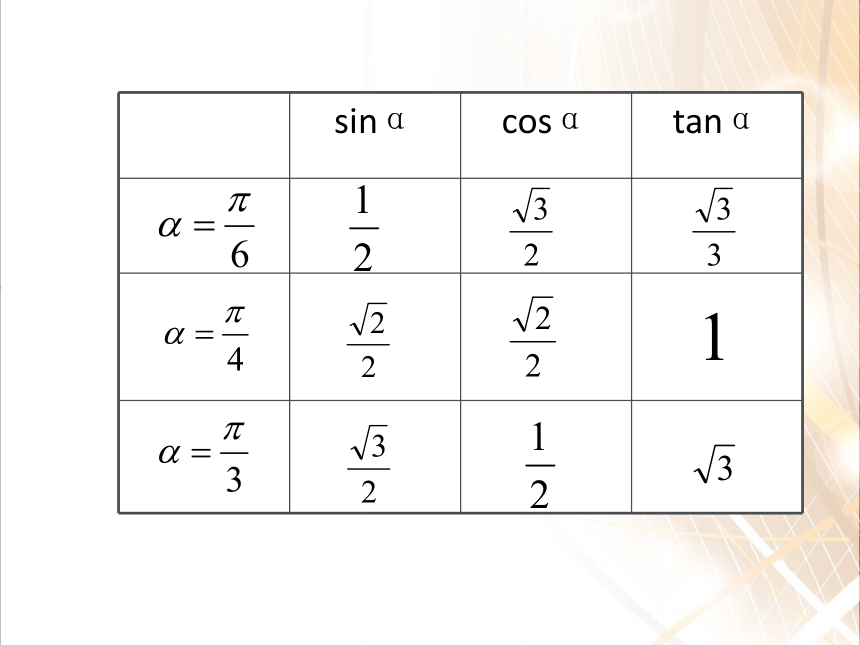








文档简介
课件42张PPT。1.2.1 任意角的三角函数 你能回忆一下初中学过的锐角三角函数(正弦sinA,余弦cosA,正切tanA)的定义吗?正弦——锐角的对边与斜边的比
余弦——锐角的邻边与斜边的比
正切——锐角的对边与邻边的比P(x,y)?的终边 r?锐角三角函数定义思考:
在终边上移动点P的位置,这三个比值会改变吗? flash如何用直角坐标系内点的坐标表示锐角三角形的三角函数? 在直角坐标系中,我们称以原点O为圆心,以单位长度为半径的圆为单位圆(即:r=1).r=1 当α为任意角,它的终边与单位圆交于点P(x,y),那么 (1) 叫做α的正弦,记作
sinα,即sinα= = y ; (2) 叫做α的余弦,记作
cosα,即cosα= = x ; (3) 叫做α的正切(tangent),记作tanα, 即tanα= (x≠0).正弦函数:同理:余弦函数:正切函数:上面三个函数统称三角函数任意角三角函数的定义:定义域:R定义域:R定义域: 正弦、余弦,正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数。以上三种函数统称三角函数.关键:
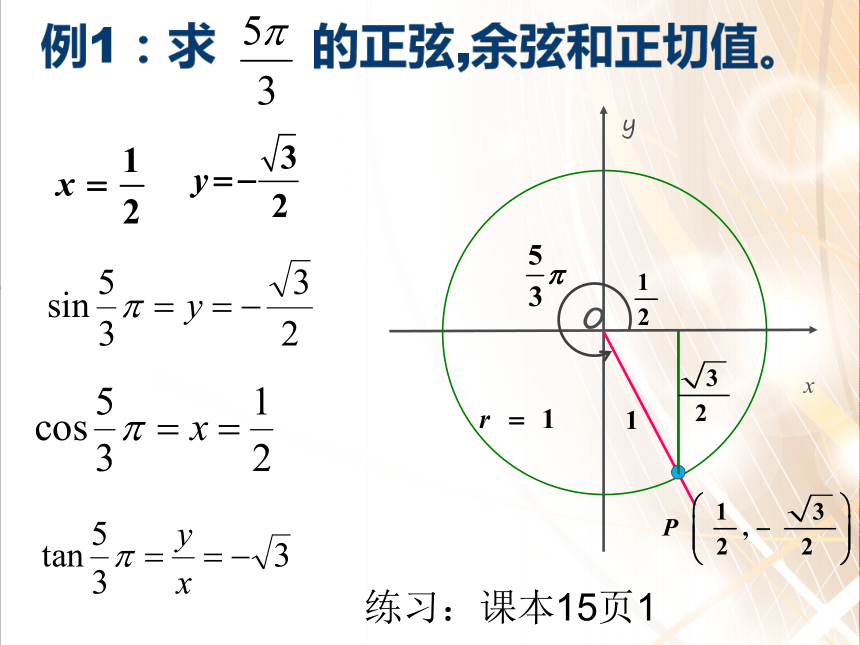
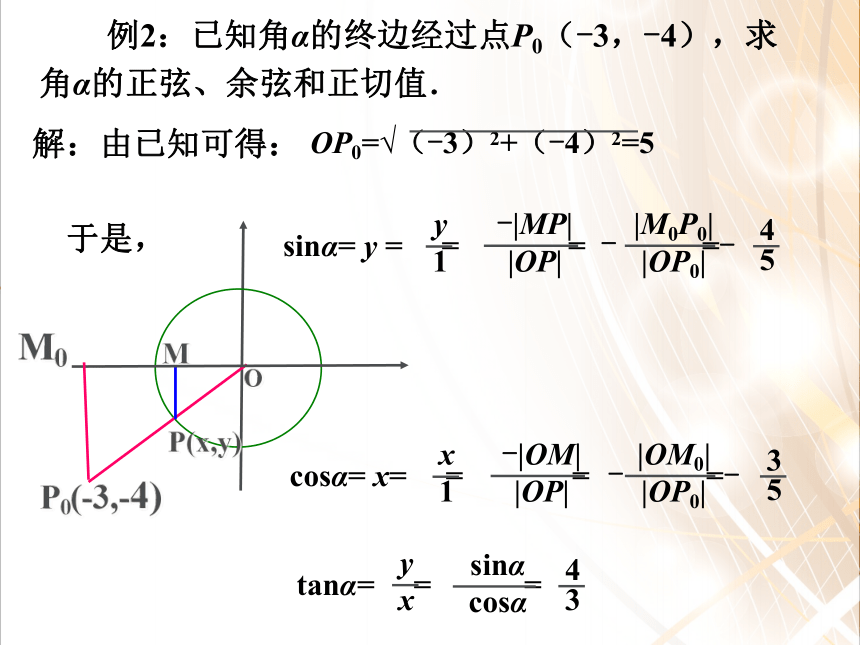
求出α角终边与单位圆的交点。思考:如何求α角的三角函数值?例1:求 的正弦,余弦和正切值。例1:求 的正弦,余弦和正切值。yxO练习:课本15页1 例2:已知角α的终边经过点P0(-3,-4),求角α的正弦、余弦和正切值.解:由已知可得:于是,MP(x,y)O 在平面直角坐标系中,设角 的终边上
任意一点P的坐标是(x,y),它到原点的距离
为r,
(r=|OP|= )>0xyxMr4.已知角α的终边经过点P(x,-6)且则x的值为______.10练习:课本15页2全优84页限时规范训练【例1】 已知角α的终边经过点P(24a,-7a)(a∈R且a≠0),求α的正弦值、余弦值和正切值.【解析】由已知得r=|OP|==25|a|,若a>0,则r=25a,于是sin α=cos α=tan α=全优第7页典例剖析【例1】 已知角α的终边经过点P(24a,-7a)(a∈R且a≠0),求α的正弦值、余弦值和正切值.【解析】由已知得r=|OP|==25|a|,若a<0,则r=-25a,于是sin α=cos α=tan α=三角函数值的符号问题 根据刚才所学的知识,将正弦、余弦、正切函数的值在各象限的符号填入下图中.(课本13页)-+---+-++-+10-1010-10在sin和cos的图像中,两个“+”号之间是1,两个“-”号之间是-1,一“+”一“-”之间是0.练习:课本15页3,4例3:求证:当且仅当下列不等式组成立时,角θ为第三象限角, 反之也对.证明:当θ为第三象限角时,上式显然成立 因为①式sinθ<0成立,所以θ角的终边可能位于 第三或第四象限,也可能与y轴的非正半轴重合; 又因为②式tanθ>0成立,所以θ角的终边可能位于第一或第三象限.下面我们证明如果①②式都成立,那么θ为第三象限角. 例3:求证:当且仅当下列不等式组成立时,角θ为第三象限角. 因为①、②式都成立,所以θ角的终边只能位于第三象限,于是角θ为第三象限角.4.若三角形的两内角A,B满足sin A·cos B<0,则此三角形的形状为( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定B全优第9页基础夯实6.已知tan α>0且sin α+cos α>0,那么α的终边在第________象限.全优第9页能力提高一5.8cos 270°+6sin 180°+4tan 0°+2sin 90°=________.2【解析】原式=8×0+6×0+4×0+2×1=2.全优第9页基础夯实3.已知α的终边经过点(3a-9,a+2)且sin α>0,cos α≤0,则实数a的取值范围是________.{a|-20,cos α≤0,解得-2思考:终边相同终边相同的角的集合点的坐标相同同一函数值相等 终边相同的角的同一三角函数值相等.
即有公式一 其中 作用:把求任意角的三角函数值转化为求0到2π角的三角函数值. 例4:确定下列三角函数值的符号.(1)cos250°;(3)tan(-672°);(4)tan3π.解:(1)因为250°是第三象限角,所以cos250°<0(3)因为tan(-672°)=tan(48°-2×360°),而48°是第一象限角,所以tan(-672°)>0(2)因为 是第四象限角,所以(4)因为tan3π=tan(π+2π)=tanπ,而π的终边在x轴上,所以tan3π=0练习:课本15页5例5:求下列三角函数值:3.求下列各式的值:(1)sin(-1 410°);【解析】(1)sin(-1 410°)=sin(-4×360°+30°)=sin 30°全优第8页变式训练思考:如图,设角α为第一象限角,
角α的正弦、余弦值能否分别用一条线段表示?思考:若角α为第三象限角,角α的正弦值和余弦值分别用哪条线段表示?flash|sinα|=|y|=|MP||cosα|=|x|=|OM| 我们知道,直角坐标系内点的坐标与坐标轴的方向有关.类似的,如果我们可以用坐标轴的方向来规定线段OM、MP的方向,就可以使它们的取值与P点的坐标联系起来. 当线段OM与x轴同向时,OM的方向为正向,且有正值x;当线段OM与x轴反向时,OM的方向为负向,且有负值x.其中x为P点的横坐标.这样,无论哪一种情况都有 当角α的终边不在坐标轴上时,以O为始点、M为终点,规定:cosα=OM=xOM称之为余弦线 当线段MP与y轴同向时,MP的方向为正向,且有正值y;当线段MP与y轴反向时,MP的方向为负向,且有负值y.其中y为P点的纵坐标.这样,无论哪一种情况都有 同理,当角α的终边不在坐标轴上时,以M为始点、P为终点,规定:sinα =MP=yMP称之为正弦线 像OM、MP这种被看作带有方向的线段,叫做有向线段(directed line segment).注意:书写的时候要先写起点的字母,再写终点的字母,不能颠倒!思考:能用有向线段来表示正切吗?
(正切线)几何画板演示 2.作出下列各角的正弦线、余弦线和正切线.(课本17页)MT 解:(3)如图,MP为正弦线, OM为余弦线, AT为正切线. 2.作出下列各角的正弦线、余弦线和正切线,并求出它们的正弦、余弦和正切的值.(4)如图,
MP为正弦线,
OM为余弦线,
AT为正切线.MT 作三角函数线的具体步骤如下:
1) 画单位圆,2) 设α的终边与单位圆交于点P,作PM⊥x轴于M,则有向线段MP是正弦线。3) 有向线段OM是余弦线。4) 设单位圆与x轴的非负半轴交于点A(1,0),过点A作垂线与角α的终边(或其反向延长线)交于点T,则有向线段AT就是正切线。
余弦——锐角的邻边与斜边的比
正切——锐角的对边与邻边的比P(x,y)?的终边 r?锐角三角函数定义思考:
在终边上移动点P的位置,这三个比值会改变吗? flash如何用直角坐标系内点的坐标表示锐角三角形的三角函数? 在直角坐标系中,我们称以原点O为圆心,以单位长度为半径的圆为单位圆(即:r=1).r=1 当α为任意角,它的终边与单位圆交于点P(x,y),那么 (1) 叫做α的正弦,记作
sinα,即sinα= = y ; (2) 叫做α的余弦,记作
cosα,即cosα= = x ; (3) 叫做α的正切(tangent),记作tanα, 即tanα= (x≠0).正弦函数:同理:余弦函数:正切函数:上面三个函数统称三角函数任意角三角函数的定义:定义域:R定义域:R定义域: 正弦、余弦,正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数。以上三种函数统称三角函数.关键:
求出α角终边与单位圆的交点。思考:如何求α角的三角函数值?例1:求 的正弦,余弦和正切值。例1:求 的正弦,余弦和正切值。yxO练习:课本15页1 例2:已知角α的终边经过点P0(-3,-4),求角α的正弦、余弦和正切值.解:由已知可得:于是,MP(x,y)O 在平面直角坐标系中,设角 的终边上
任意一点P的坐标是(x,y),它到原点的距离
为r,
(r=|OP|= )>0xyxMr4.已知角α的终边经过点P(x,-6)且则x的值为______.10练习:课本15页2全优84页限时规范训练【例1】 已知角α的终边经过点P(24a,-7a)(a∈R且a≠0),求α的正弦值、余弦值和正切值.【解析】由已知得r=|OP|==25|a|,若a>0,则r=25a,于是sin α=cos α=tan α=全优第7页典例剖析【例1】 已知角α的终边经过点P(24a,-7a)(a∈R且a≠0),求α的正弦值、余弦值和正切值.【解析】由已知得r=|OP|==25|a|,若a<0,则r=-25a,于是sin α=cos α=tan α=三角函数值的符号问题 根据刚才所学的知识,将正弦、余弦、正切函数的值在各象限的符号填入下图中.(课本13页)-+---+-++-+10-1010-10在sin和cos的图像中,两个“+”号之间是1,两个“-”号之间是-1,一“+”一“-”之间是0.练习:课本15页3,4例3:求证:当且仅当下列不等式组成立时,角θ为第三象限角, 反之也对.证明:当θ为第三象限角时,上式显然成立 因为①式sinθ<0成立,所以θ角的终边可能位于 第三或第四象限,也可能与y轴的非正半轴重合; 又因为②式tanθ>0成立,所以θ角的终边可能位于第一或第三象限.下面我们证明如果①②式都成立,那么θ为第三象限角. 例3:求证:当且仅当下列不等式组成立时,角θ为第三象限角. 因为①、②式都成立,所以θ角的终边只能位于第三象限,于是角θ为第三象限角.4.若三角形的两内角A,B满足sin A·cos B<0,则此三角形的形状为( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定B全优第9页基础夯实6.已知tan α>0且sin α+cos α>0,那么α的终边在第________象限.全优第9页能力提高一5.8cos 270°+6sin 180°+4tan 0°+2sin 90°=________.2【解析】原式=8×0+6×0+4×0+2×1=2.全优第9页基础夯实3.已知α的终边经过点(3a-9,a+2)且sin α>0,cos α≤0,则实数a的取值范围是________.{a|-2
即有公式一 其中 作用:把求任意角的三角函数值转化为求0到2π角的三角函数值. 例4:确定下列三角函数值的符号.(1)cos250°;(3)tan(-672°);(4)tan3π.解:(1)因为250°是第三象限角,所以cos250°<0(3)因为tan(-672°)=tan(48°-2×360°),而48°是第一象限角,所以tan(-672°)>0(2)因为 是第四象限角,所以(4)因为tan3π=tan(π+2π)=tanπ,而π的终边在x轴上,所以tan3π=0练习:课本15页5例5:求下列三角函数值:3.求下列各式的值:(1)sin(-1 410°);【解析】(1)sin(-1 410°)=sin(-4×360°+30°)=sin 30°全优第8页变式训练思考:如图,设角α为第一象限角,
角α的正弦、余弦值能否分别用一条线段表示?思考:若角α为第三象限角,角α的正弦值和余弦值分别用哪条线段表示?flash|sinα|=|y|=|MP||cosα|=|x|=|OM| 我们知道,直角坐标系内点的坐标与坐标轴的方向有关.类似的,如果我们可以用坐标轴的方向来规定线段OM、MP的方向,就可以使它们的取值与P点的坐标联系起来. 当线段OM与x轴同向时,OM的方向为正向,且有正值x;当线段OM与x轴反向时,OM的方向为负向,且有负值x.其中x为P点的横坐标.这样,无论哪一种情况都有 当角α的终边不在坐标轴上时,以O为始点、M为终点,规定:cosα=OM=xOM称之为余弦线 当线段MP与y轴同向时,MP的方向为正向,且有正值y;当线段MP与y轴反向时,MP的方向为负向,且有负值y.其中y为P点的纵坐标.这样,无论哪一种情况都有 同理,当角α的终边不在坐标轴上时,以M为始点、P为终点,规定:sinα =MP=yMP称之为正弦线 像OM、MP这种被看作带有方向的线段,叫做有向线段(directed line segment).注意:书写的时候要先写起点的字母,再写终点的字母,不能颠倒!思考:能用有向线段来表示正切吗?
(正切线)几何画板演示 2.作出下列各角的正弦线、余弦线和正切线.(课本17页)MT 解:(3)如图,MP为正弦线, OM为余弦线, AT为正切线. 2.作出下列各角的正弦线、余弦线和正切线,并求出它们的正弦、余弦和正切的值.(4)如图,
MP为正弦线,
OM为余弦线,
AT为正切线.MT 作三角函数线的具体步骤如下:
1) 画单位圆,2) 设α的终边与单位圆交于点P,作PM⊥x轴于M,则有向线段MP是正弦线。3) 有向线段OM是余弦线。4) 设单位圆与x轴的非负半轴交于点A(1,0),过点A作垂线与角α的终边(或其反向延长线)交于点T,则有向线段AT就是正切线。
