6.1.2平行四边形的性质

(共14张PPT)
课题：6.1.2 平行四边形的性质（2）
新课导入
平行四边形的性质
边
对角线：
两组对边分别相等
两组对边分别平行
角：
对角相等
B
C
D
A
O
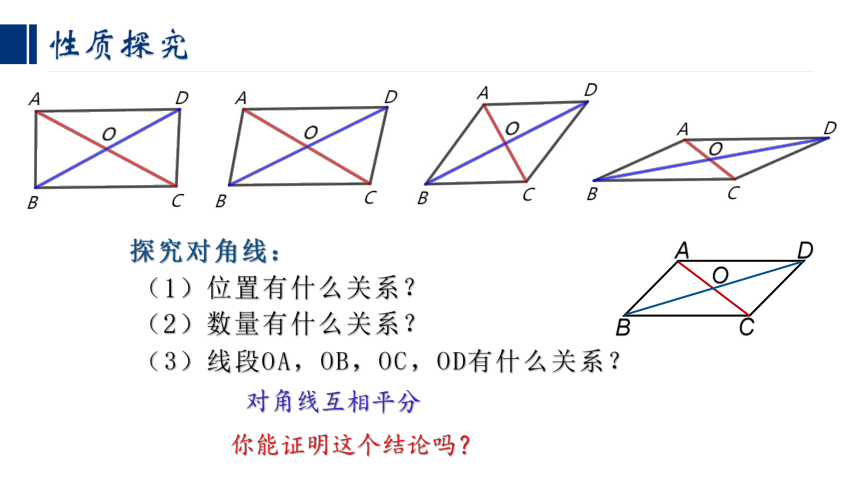
性质探究
B
C
D
A
O
（2）数量有什么关系？
（1）位置有什么关系？
（3）线段OA，OB，OC，OD有什么关系？
对角线互相平分
你能证明这个结论吗？
探究对角线：
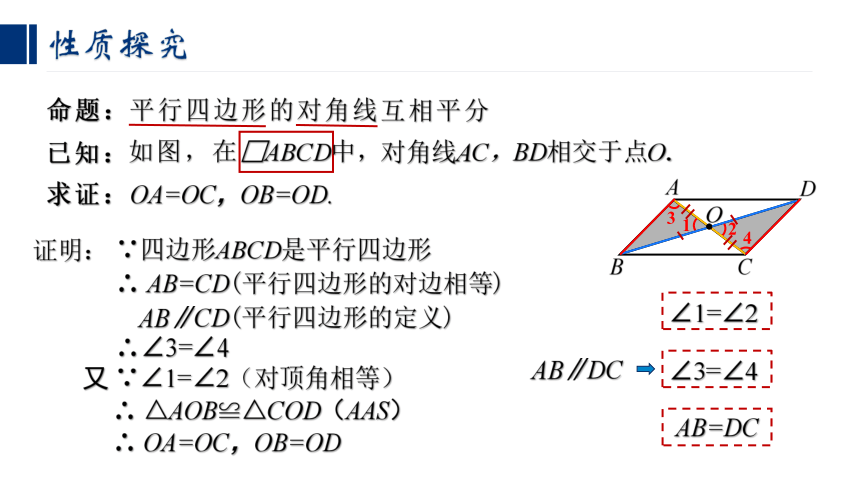
性质探究
命题：平行四边形的对角线互相平分
B
C
D
A
O
已知：
求证：OA=OC，OB=OD.
1
2
∠1=∠2
AB∥DC
∠3=∠4
3
4
证明：
∵四边形ABCD是平行四边形
∴ AB=CD(平行四边形的对边相等)
∴∠3=∠4
∴ △AOB≌△COD（AAS）
∴ OA=OC，OB=OD
AB∥CD(平行四边形的定义)
又 ∵∠1=∠2（对顶角相等）
如图，在□ABCD中，
对角线AC，BD相交于点O.
AB=DC
性质探究
B
C
D
A
O
平行四边形对角线互相平分
平行四边形的性质：
对角线互相平分
几何语言：
∵四边形ABCD是平行四边形
∴OA=OC=AC AC=2OA=2OC
OB=OD=BD BD=2OB=2OD
技能体验
已知：如图，□ABCD的对角线AC与BD相交于点O，过点O
的直线与AD，BC分别相交于点E，F.
求证：OE=OF.
O
D
C
B
A
E
F
2
∵四边形ABCD是平行四边形
证明：
∴AO=CO(平行四边形对角线相互平分)
AD∥BC（平行四边形定义）
∴∠1=∠2
∵∠3=∠4
1
3
4
∴△AOE≌△COF（ASA）
∴OE=OF
∵四边形ABCD是平行四边形
证明：
∴OA=OC
AD∥BC
∴∠1=∠2
∵∠3=∠4
∴△AOE≌△COF（ASA）
∴OE=OF
∵点E,F分别在DA,BC的延长线上
∴DE∥BF
技能体验
O
D
C
B
A
E
F
●
●
变式：若直线EF与边DA、BC的延长线分别交于点E、F，上述结论OE=OF是否仍然成立？
2
1
3
4
拓展提升
思考：将直线EF绕点O旋转的过程中，上述结论OE=OF是否仍然成立？
F
E
F
O
D
C
B
A
E
●
●
拓展提升
O
D
C
B
A
E
F
F
O
D
C
B
A
E
F
O
D
C
B
A
E
△AOE≌△COF
OE=OF
O
D
C
B
A
E
F
思考第一幅图中：
（1）全等三角形有哪些？
（2）四边形AOFB与四边形
COED什么关系？
（3）四边形AEFB与四边形
CFOD什么关系？
学以致用
如图，在平行四边形ABCD中，AC，BD为对角线，
BC＝6，BC边上的高为4，则图中阴影部分的面积为(　　)
A. 3 B. 6
C. 12 D. 24
C
S阴影=
O
学以致用
如图，在平行四边形ABCD中，AC，BD为对角线，
BC＝6，BC边上的高为4，则图中阴影部分的面积为(　　)
A. 3 B. 6
C. 12 D. 24
C
S阴影=
O
课堂小结
平行四边形的性质
边
对角线：
两组对边分别相等
两组对边分别平行
角：
对角相等
B
C
D
A
O
对角线互相平分
当堂练习
如图，□ABCD的对角线AC与BD相交于点O，∠ADB= 90°，OA=6，OB=3.
求AD和AC的长度.
B
D
A
C
O
解：
∴△ADO是直角三角形
又∵∠ADB= 90°
∴AC=2OA=12
∵四边形ABCD是平行四边形
3
3
6
6
按下暂停键，完成练习后再回来吧！
同学们再见！