6.2.1平四边形的判定

(共15张PPT)
6.2 平行四边形的判定（1）
性质
判定
定义
B
C
D
A
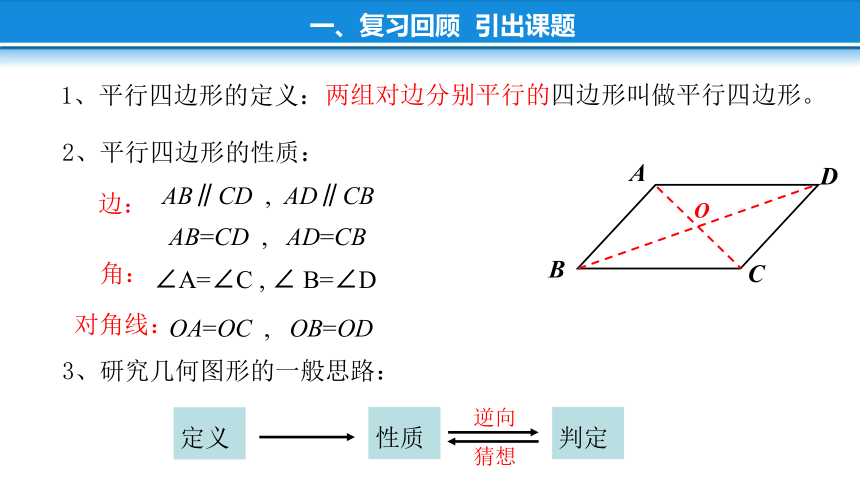
两组对边分别平行的四边形叫做平行四边形。
1、平行四边形的定义：
边：
2、平行四边形的性质：
3、研究几何图形的一般思路：
逆向猜想
一、复习回顾 引出课题
角：
对角线：
AB∥CD , AD∥CB
AB=CD , AD=CB
∠A=∠C , ∠ B=∠D
O
OA=OC , OB=OD
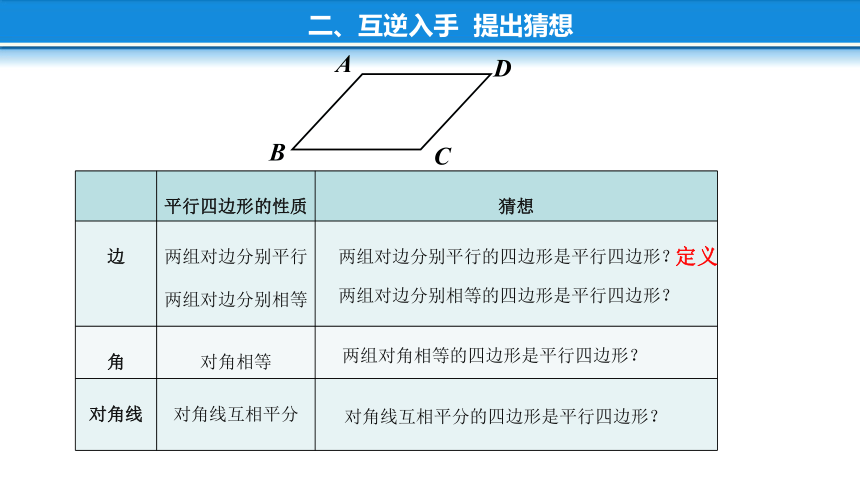
平行四边形的性质
猜想
边 两组对边分别平行 两组对边分别相等
角 对角相等
对角线 对角线互相平分
两组对角相等的四边形是平行四边形？
对角线互相平分的四边形是平行四边形？
两组对边分别相等的四边形是平行四边形？
两组对边分别平行的四边形是平行四边形？
B
C
D
A
二、互逆入手 提出猜想
定义
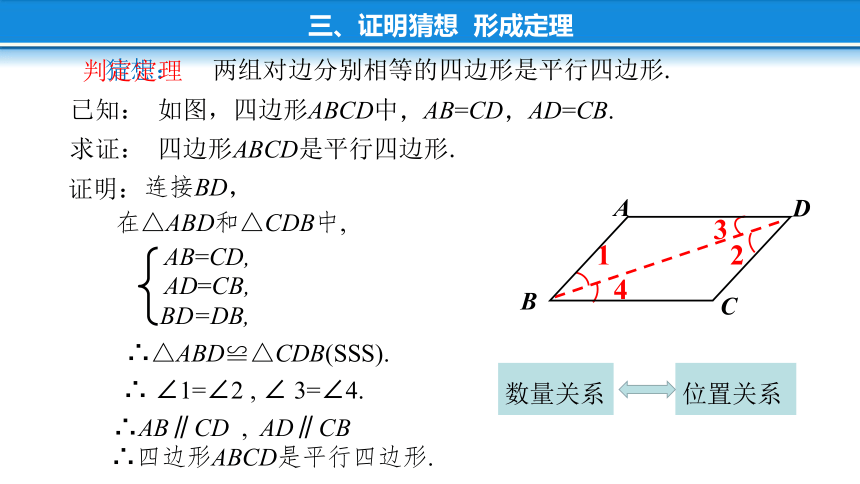
已知： 如图，四边形ABCD中，AB=CD，AD=CB.
求证： 四边形ABCD是平行四边形.
连接BD，
在△ABD和△CDB中,
AB=CD,
BD=DB,
AD=CB,
∴△ABD≌△CDB(SSS).
∴ ∠1=∠2 , ∠ 3=∠4.
∴AB∥CD , AD∥CB
∴四边形ABCD是平行四边形.
证明：
1
4
2
3
猜想：
两组对边分别相等的四边形是平行四边形.
判定定理
B
C
D
A
数量关系
位置关系
三、证明猜想 形成定理
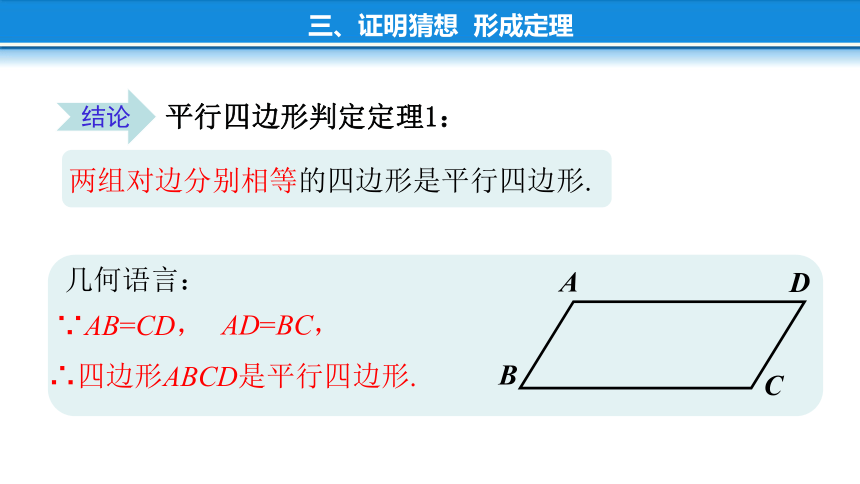
两组对边分别相等的四边形是平行四边形.
∵AB=CD，
AD=BC，
∴四边形ABCD是平行四边形.
几何语言：
平行四边形判定定理1：
B
D
C
A
结论
三、证明猜想 形成定理
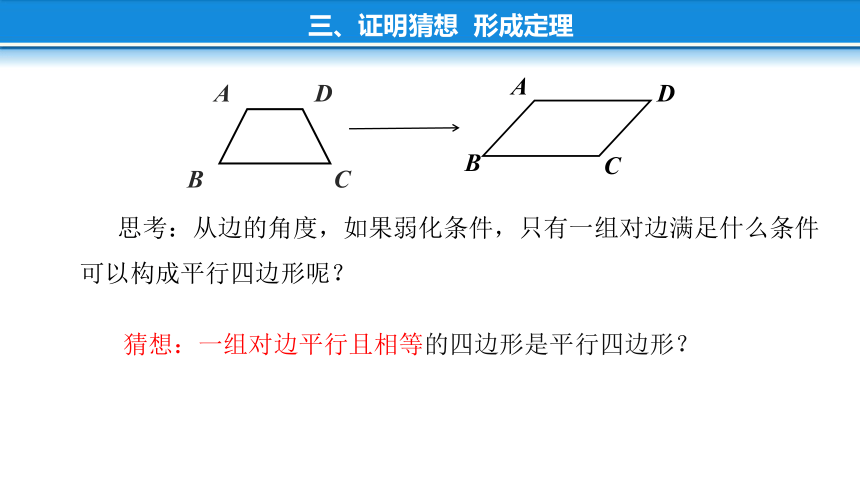
猜想：一组对边平行且相等的四边形是平行四边形？
B
C
D
A
B
C
A
D
思考：从边的角度，如果弱化条件，只有一组对边满足什么条件
可以构成平行四边形呢？
三、证明猜想 形成定理
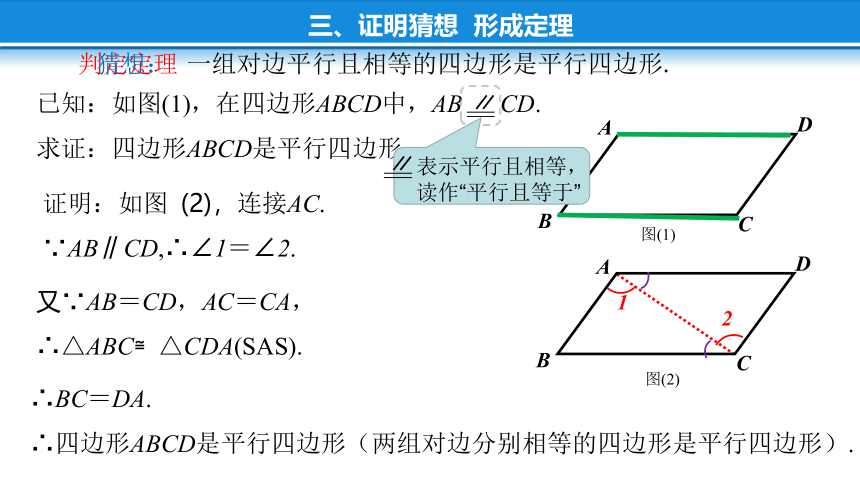
已知：如图(1)，在四边形ABCD中，AB CD.
求证：四边形ABCD是平行四边形.
1
2
D
A
B
C
图(1)
D
A
B
C
图(2)
证明：如图 (2)，连接AC.
∵AB∥CD,∴∠1＝∠2.
表示平行且相等，读作“平行且等于”
判定定理
猜想：
一组对边平行且相等的四边形是平行四边形.
∴BC＝DA.
∴四边形ABCD是平行四边形（两组对边分别相等的四边形是平行四边形）.
又∵AB＝CD，AC＝CA，
∴△ABC≌△CDA(SAS).
三、证明猜想 形成定理
一组对边平行且相等的四边形是平行四边形.
∵AB=CD，
AB∥CD，
∴四边形ABCD是平行四边形.
几何语言：
平行四边形判定定理2：
B
D
C
A
结论
三、证明猜想 形成定理
平行四边形的判定方法：边
判定方法1（定义法）：两组对边分别平行的四边形是平行四边形.
判定方法2：两组对边分别相等的四边形是平行四边形.
判定方法3：一组对边平行且相等的四边形是平行四边形.
数学思想方法：归纳、类比、化归.
研究思路：
定义
性质
判定
逆向猜想
三、证明猜想 形成定理
【例题1】如图，在平行四边形ABCD中，点E，F分别在BC，AD的中点，求证：四边形AECF是平行四边形．
证明：∵四边形ABCD是平行四边形，
∴AD=BC，AB=DC，∠B=∠D.
∴AF=CE, BE=DF
∴△ABE≌△CDF（SAS）∴AE=CF
∵AE=FC，AF=CE，∴四边形AECF是平行四边形．
∵点E，F分别在BC，AD的中点,
∴AF=DF= AD，CE=BE= BC.
四、技能提升，运用判定
思考：还有其它方法吗？
【例题1】如图，在平行四边形ABCD中，点E，F分别在BC，AD的中点，求证：四边形AECF是平行四边形．
证明：∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC.
∴AF=CE，AF∥CE.
∴四边形AECF是平行四边形．
∵点E，F分别在BC，AD的中点，
∴AF= AD，CE= BC.
四、技能提升，运用判定
【例题2】已知：如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE=CF，DF∥BE．求证：四边形ABCD为平行四边形．
证明：∵AB∥CD
∴∠1=∠2
∵DF∥BE
∴∠DFA=∠BEC
∴∠AEB=∠DFC
∵ AE=CF
∴△AEB≌△CFD（ASA）
∴AB=CD
∵AB∥CD
∴四边形ABCD为平行四边形．
四、技能提升，运用判定
1
2
平行四边形
归纳、类比、化归
定义
性质
判定
（从边的角度)
五、课堂小结
如图，在平行四边形ABCD中，已知AE、CF分别是∠DAB、∠BCD的角平分线，试证明四边形AFCE是平行四边形．
∵AE、CF分别是∠DAB、 ∠BCD的角平分线
∴△ABE≌△CDF(ASA).
∴BE=DF. ∴AF=CE . ∵AF∥CE,
∴四边形AFCE是平行四边形
(一组对边平行且相等的四边形是平行四边形）
六、当堂检测
证明：∵在平行四边形ABCD中，
∴AD∥BC，AB=CD,∠B=∠D, ∠DAB= ∠BCD
∴∠BAE=∠DCF= ∠DAB= ∠BCD .
请完成《平行四边形判定（1）》配套练习。
自主作业
必做：基础题（1-7题）
选做：拓展题（8题）