江苏省东台市南沈灶镇中学(苏科版)九年级下册课件:6.5相似三角形的性质(共19张PPT)
文档属性
| 名称 | 江苏省东台市南沈灶镇中学(苏科版)九年级下册课件:6.5相似三角形的性质(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 206.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-03 16:04:38 | ||
图片预览


文档简介
课件19张PPT。相似三角形的判定和性质的复习课南沈灶镇中学九年级数学备课组 徐中海概念复习 相似三角形的性质相似三角形的定义
相似三角形的判定
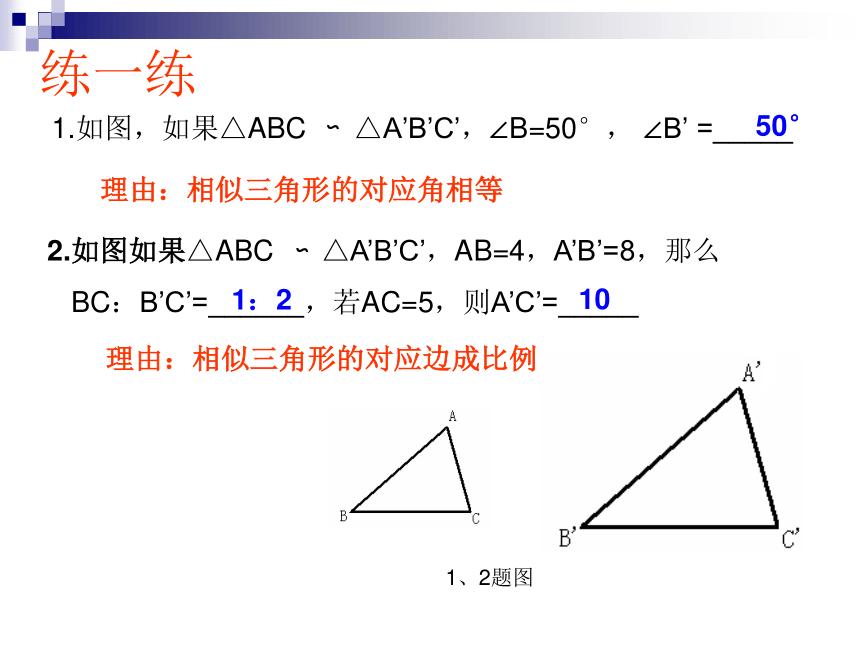
练一练1.如图,如果△ABC △A’B’C’,∠B=50°, ∠B’ =_____∽50°理由:相似三角形的对应角相等 2.如图如果△ABC △A’B’C’,AB=4,A’B’=8,那么
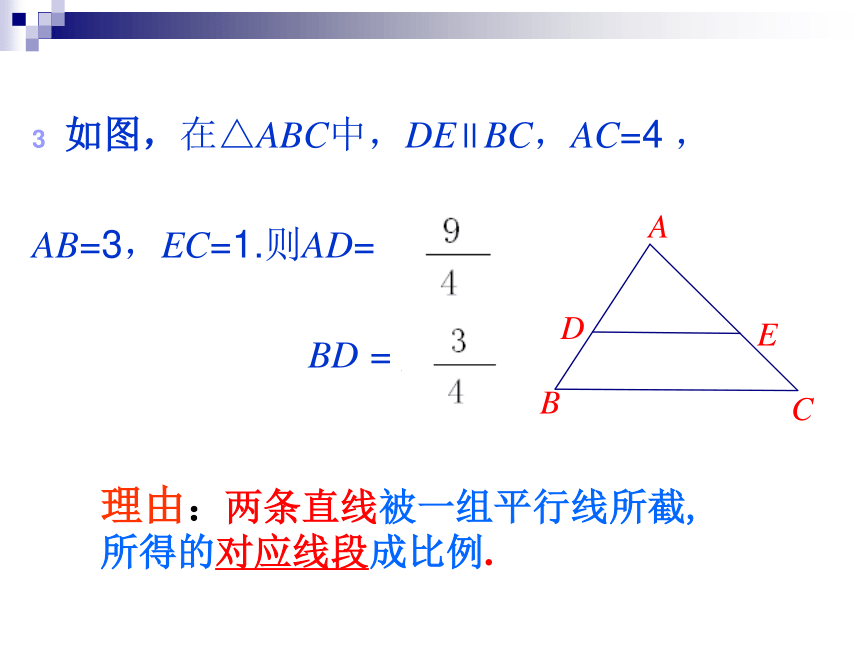
BC:B’C’=______,若AC=5,则A’C’=_____∽理由:相似三角形的对应边成比例1:2101、2题图如图,在△ABC中,DE∥BC,AC=4 ,
AB=3,EC=1.则AD= ______,
BD = ______
理由:两条直线被一组平行线所截,
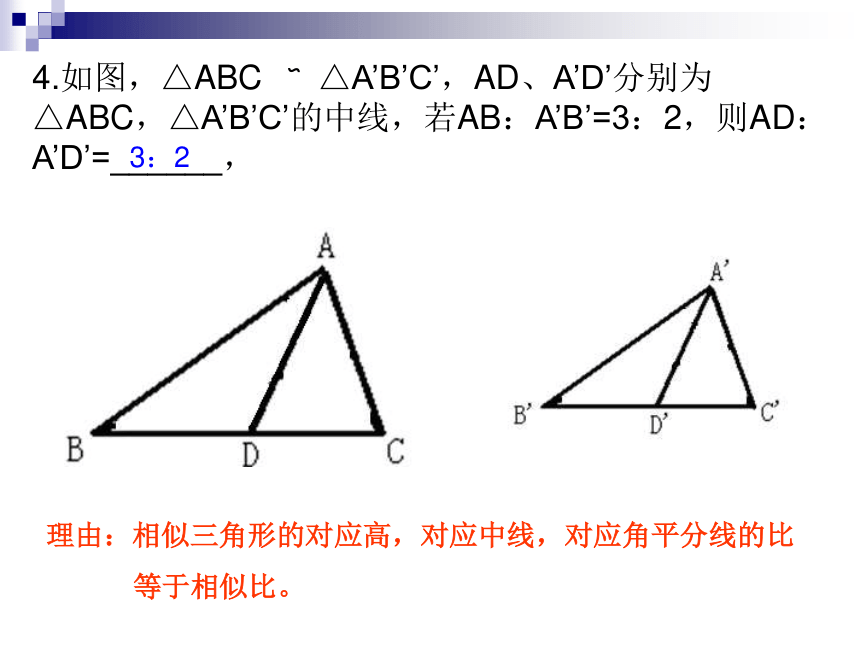
所得的对应线段成比例.4.如图,△ABC △A’B’C’,AD、A’D’分别为 △ABC,△A’B’C’的中线,若AB:A’B’=3:2,则AD:A’D’=______,∽3:2理由:相似三角形的对应高,对应中线,对应角平分线的比
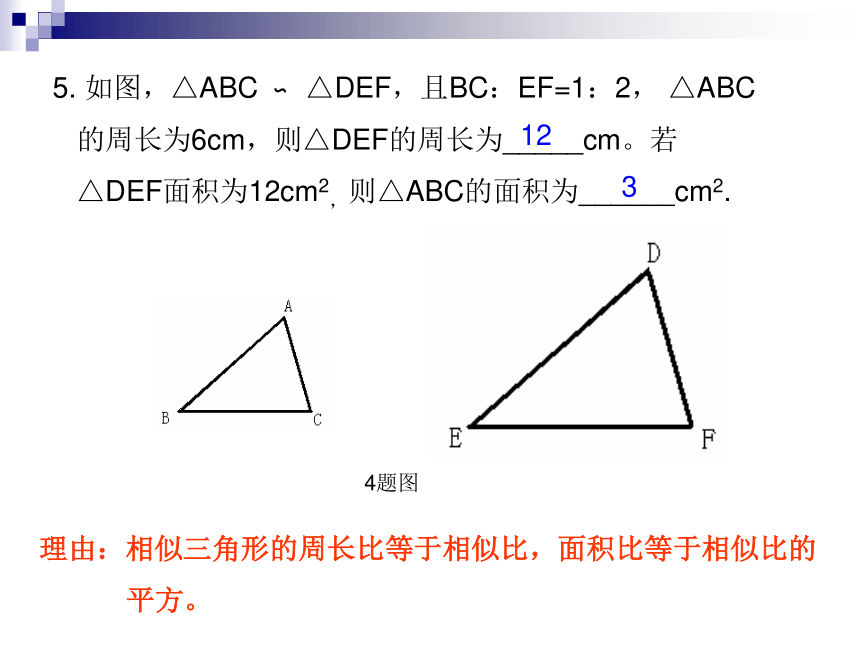
等于相似比。5. 如图,△ABC △DEF,且BC:EF=1:2, △ABC
的周长为6cm,则△DEF的周长为_____cm。若
△DEF面积为12cm2,则△ABC的面积为______cm2. ∽1234题图理由:相似三角形的周长比等于相似比,面积比等于相似比的
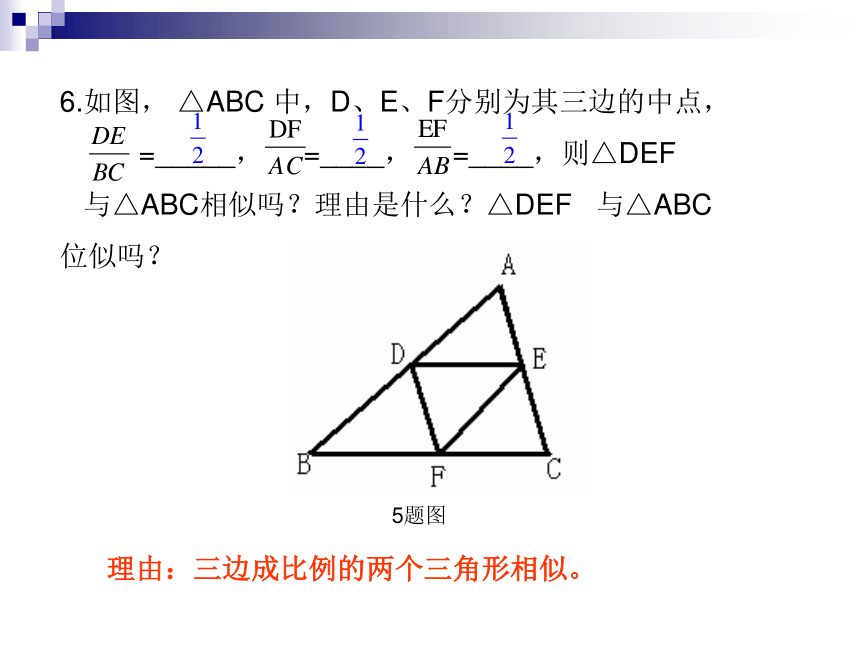
平方。6.如图, △ABC 中,D、E、F分别为其三边的中点,
=_____, =____, =____,则△DEF
与△ABC相似吗?理由是什么?△DEF 与△ABC
位似吗?
5题图理由:三边成比例的两个三角形相似。6题图7.(1)如图,若 ,则 △ABC 与
△ AED相似吗? _______(2) 若∠B=50°,则∠1=________时,△ABC △AED∽理由:两边成比例,且夹角相等的
两个三角形相似。理由:两角分别相等的两个三角形相似。(3)若△ABC △AED,可得 ,
则AD·AB=_________∽相似50°AE·ACAC理由:三角形相似的对应边成比例。8.如图,上题中ED进行平移,当点
E与点C重合时,∠1仍与∠B相等
时,填空 AD·AB =
拓展延伸AC2请证明你的结论变题1,若△ABC中,AC2=AD·AB,你能说明
∠1与∠B相等吗?因为AC2=AD·AB 又因为∠A= ∠A∽所以△ABC △CBD所以∠1= ∠B解:∠1= ∠B变式训练变题2,将8题中∠ACB变化为90°,CD⊥AB, 你能得出AC2=AD·AB吗?你还能得出类似的结论吗?变式训练例题教学在Rt△ABC中,∠ACB=90°,CF⊥AB,垂足为F,D为
AC上任意一点,CE ⊥BD,垂足为E,连接EF,
求 证:∠1= ∠A。证明:因为∠BCD= ∠CEB=90°
∠CBD= ∠CBE
所以△BCD △BEC
∽ 所以BC2=BD·BE 同理BC2=BF·BA
所以BD·BE=BF·BA又因为∠DBA= ∠EBF
所以△DBA △FBE ∽所以∠1= ∠A变题1:△ABC中,∠ACB=90°,D为BC上一点,CE⊥AD,
垂足为E,连结BE,且∠1= ∠2,求证:CD=BD。证明:因为∠ACB=90°, ∠CED=90 °
∠CDA= ∠CDE 所以△ACD △CED∽所以CD2=DE·DA同理BD2=DE·DA所以CD2=BD2因为CD>0,BD>0所以CD=BD变题2:如图,△ABC中,∠ACB=90°,CE⊥AD,垂足为E,
连接EB,D为BC的中点。求证:∠1= ∠2证明:因为∠ACD=90°,∠CED=90 °
∠CDE= ∠CDA所以△ACD △CED∽所以CD2=AD·ED又因为BD=CD 所以BD2=AD·ED又因为∠ADB= ∠ADB所以△BED △ABD所以∠1= ∠2∽ 如图:四边形ABCD中∠A=∠BCD=90°,过C作对角线BD的垂线交BD、AD于点 E、F,
求证: ;
巩固练习变式:如图:若过BD上任一点E作BD的垂线交
AD、CD于F、G,又有什么结论呢?你
会证明吗 ?
如图,在直角梯形ABCD中,AB∥CD, AB⊥BC,对角线AC⊥BD,垂足为E,AD=BD,过点E作EF∥AB交AD于F, 试说明 (1)AF=BE (2) AF2=AE·EC利用等线段代换巩固练习今天你收获了什么? 补充习题 p40-41作业谢谢各位领导
和老师的指导
相似三角形的判定
练一练1.如图,如果△ABC △A’B’C’,∠B=50°, ∠B’ =_____∽50°理由:相似三角形的对应角相等 2.如图如果△ABC △A’B’C’,AB=4,A’B’=8,那么
BC:B’C’=______,若AC=5,则A’C’=_____∽理由:相似三角形的对应边成比例1:2101、2题图如图,在△ABC中,DE∥BC,AC=4 ,
AB=3,EC=1.则AD= ______,
BD = ______
理由:两条直线被一组平行线所截,
所得的对应线段成比例.4.如图,△ABC △A’B’C’,AD、A’D’分别为 △ABC,△A’B’C’的中线,若AB:A’B’=3:2,则AD:A’D’=______,∽3:2理由:相似三角形的对应高,对应中线,对应角平分线的比
等于相似比。5. 如图,△ABC △DEF,且BC:EF=1:2, △ABC
的周长为6cm,则△DEF的周长为_____cm。若
△DEF面积为12cm2,则△ABC的面积为______cm2. ∽1234题图理由:相似三角形的周长比等于相似比,面积比等于相似比的
平方。6.如图, △ABC 中,D、E、F分别为其三边的中点,
=_____, =____, =____,则△DEF
与△ABC相似吗?理由是什么?△DEF 与△ABC
位似吗?
5题图理由:三边成比例的两个三角形相似。6题图7.(1)如图,若 ,则 △ABC 与
△ AED相似吗? _______(2) 若∠B=50°,则∠1=________时,△ABC △AED∽理由:两边成比例,且夹角相等的
两个三角形相似。理由:两角分别相等的两个三角形相似。(3)若△ABC △AED,可得 ,
则AD·AB=_________∽相似50°AE·ACAC理由:三角形相似的对应边成比例。8.如图,上题中ED进行平移,当点
E与点C重合时,∠1仍与∠B相等
时,填空 AD·AB =
拓展延伸AC2请证明你的结论变题1,若△ABC中,AC2=AD·AB,你能说明
∠1与∠B相等吗?因为AC2=AD·AB 又因为∠A= ∠A∽所以△ABC △CBD所以∠1= ∠B解:∠1= ∠B变式训练变题2,将8题中∠ACB变化为90°,CD⊥AB, 你能得出AC2=AD·AB吗?你还能得出类似的结论吗?变式训练例题教学在Rt△ABC中,∠ACB=90°,CF⊥AB,垂足为F,D为
AC上任意一点,CE ⊥BD,垂足为E,连接EF,
求 证:∠1= ∠A。证明:因为∠BCD= ∠CEB=90°
∠CBD= ∠CBE
所以△BCD △BEC
∽ 所以BC2=BD·BE 同理BC2=BF·BA
所以BD·BE=BF·BA又因为∠DBA= ∠EBF
所以△DBA △FBE ∽所以∠1= ∠A变题1:△ABC中,∠ACB=90°,D为BC上一点,CE⊥AD,
垂足为E,连结BE,且∠1= ∠2,求证:CD=BD。证明:因为∠ACB=90°, ∠CED=90 °
∠CDA= ∠CDE 所以△ACD △CED∽所以CD2=DE·DA同理BD2=DE·DA所以CD2=BD2因为CD>0,BD>0所以CD=BD变题2:如图,△ABC中,∠ACB=90°,CE⊥AD,垂足为E,
连接EB,D为BC的中点。求证:∠1= ∠2证明:因为∠ACD=90°,∠CED=90 °
∠CDE= ∠CDA所以△ACD △CED∽所以CD2=AD·ED又因为BD=CD 所以BD2=AD·ED又因为∠ADB= ∠ADB所以△BED △ABD所以∠1= ∠2∽ 如图:四边形ABCD中∠A=∠BCD=90°,过C作对角线BD的垂线交BD、AD于点 E、F,
求证: ;
巩固练习变式:如图:若过BD上任一点E作BD的垂线交
AD、CD于F、G,又有什么结论呢?你
会证明吗 ?
如图,在直角梯形ABCD中,AB∥CD, AB⊥BC,对角线AC⊥BD,垂足为E,AD=BD,过点E作EF∥AB交AD于F, 试说明 (1)AF=BE (2) AF2=AE·EC利用等线段代换巩固练习今天你收获了什么? 补充习题 p40-41作业谢谢各位领导
和老师的指导
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
