专题五:鸽巢问题复习课件(共24张PPT)2023-2024学年六年级数学下学期期末核心考点集训(人教版)
文档属性
| 名称 | 专题五:鸽巢问题复习课件(共24张PPT)2023-2024学年六年级数学下学期期末核心考点集训(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 493.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-23 11:35:12 | ||
图片预览






文档简介
(共24张PPT)
专题05:鸽 巢 问 题
期末专项考点复习
人教版·六年级下册
2023-2024学年
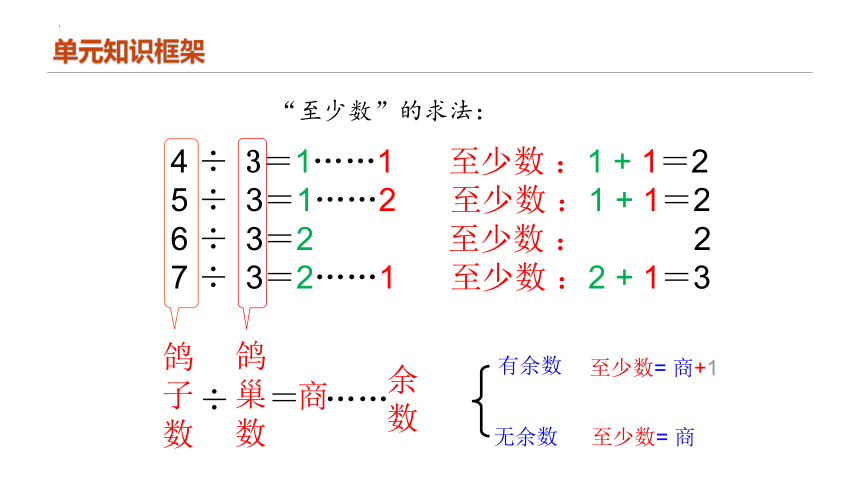
单元知识框架
4 ÷ 3=1……1 至少数 :1 + 1=2
5 ÷ 3=1……2 至少数 :1 + 1=2
6 ÷ 3=2 至少数 : 2
7 ÷ 3=2……1 至少数 :2 + 1=3
÷
=
商
……
余数
鸽子数
鸽巢数
至少数= 商+1
“至少数”的求法:
无余数
有余数
至少数= 商
www.islide.cc考点目录CONTENT“鸽巢原理”(一)“鸽巢原理”(二)应用“鸽巢原理”解决简单的实际问题考点01考点02考点03考点04考点05“鸽巢原理”(一)
/01
知识梳理
“鸽巢原理”(一):
把m个物体任意分放进n个鸽巢中(m和n是非0自然数,且m>n),那么一定有一个鸽巢中至少放进了2个物体。
举例:
把10个苹果放进9个抽屉,总有一个抽屉里至少放了2个苹果。这就是抽屉原理。
6只鸽子飞进5个鸽巢,总有一个鸽巢里至少飞进2只鸽子。这就是鸽巢原理。
典型例题
1、每个小组 6 名同学,6名同学中至少有几人在同一个季节里过生日?
题目分析:一年4个季节,所以 6 名同学中至少有2人在同一个季节里过生日。
6÷4=1……2
1+1=2
答:6名同学中至少有2人在同一个季节里过生日
典型例题
2.把7本书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书。为什么?
7÷3=2……1
跟踪练习
一副牌,取出大小王,还剩52张牌,5人每人随意抽一张,至少有几张牌是同花色的。
题目分析:一副扑克牌共54张,去掉两张王牌,剩下方块、红桃、梅花、黑桃四种花色各13张。我们把4种花色看成“4个鸽巢”,把5张扑克牌放进“4个鸽巢”中,必然有一个鸽巢至少放进2张扑克牌,即至少有2张牌是同花色的。
5÷4=1……1
1+1=2
答:即至少有2张牌是同花色的。
鸽巢原理”(二)
/02
知识梳理
“鸽巢原理”(二):
把多于kn个物体任意分进n个鸽巢中(k和n是非0自然数),那么一定有一个鸽巢中至少放进了(k+1)个物体。
典型例题
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
题目分析:
只要摸出的球数比它们的颜色种数多1,就能保证有两个球同色。
2+1=3
答:至少要摸出3个球。
跟踪练习
一天晚上,小红正要从自已放袜子的抽屉里取袜子,突然灯熄了。她知道自己的抽屉里放有白色与黄色的袜子各6只。小红至少要摸出多少只袜子,才能保证拿出一双相同颜色的袜子?
题目分析:
只要摸出的袜子只数比它们的颜色种数多1,就能保证一双相同颜色的袜子。
2+1=3
答:至少要摸出3只袜子
应用“鸽巢原理”解决简单的实际问题
/03
知识梳理
1.如果有n( n是大于0的自然数)个“鸽笼”,要保证有一个“鸽笼”至少放进了2个物品,那么至少需要有n+1个物品。
2.如果有n( n是大于0的自然数)个“鸽笼”,要保证有一个“鸽笼”至少放进了(k+1)( k是大于0的自然数)个物品,那么至少需要有(kn+1)个物品。
3.(分放的物体总数-1)÷(其中一个鸽笼里至少有的物体个数-1)=a……b(b知识梳理
4.利用“鸽巢问题”解决问题的思路和方法:
(1)分析题意,把实际问题转化成“鸽巢问题”,即弄清楚“鸽巢”(“鸽巢”是什么,有几个鸽巢)和分放的物体。
(2)设计“鸽巢”的具体形式。
(3)运用原理得出某个“鸽巢”中至少分放的物体个数,最终解决问题。
应用“鸽巢原理”解决实际问题的一般步骤:
①构造“鸽巢”,建立“数学模型”;
②把物体放入“鸽巢”,进行比较分析;
③说明理由,得出结论。
典型例题
从一副扑克牌(52张,没有大小王)中要抽出几张牌来,才能保证有一张是红桃?54张呢?
13×3+1=40
2+13×3+1=42
13
13
13
13
答:52张要抽出40张牌来,才能保证有一张是红桃
答:54张要抽出42张牌来,才能保证有一张是红桃
跟踪练习
希望小学篮球兴趣小组的同学中,最大的12岁,最小的6岁,最少从中挑选几名学生,就一定能找到两个学生年龄相同。
7+1=8
答:最少从中挑选8名学生
11只鸽子飞回4个鸽舍,至少有( )只鸽子要飞进同一个鸽舍。为什么?
11÷4=2……3
2+1=3
3
2.判断题
(1)11本书放进3个抽屉,至少有5本书要放进同一个抽屉里。( )
(2)17 只鸽子飞回5个鸽舍,至少有5个鸽子要飞进同一个鸽舍。( )
×
×
(1)5个人坐4把椅子,总有一把椅子上至少坐( )人。为什么?
(2)实验小学六(1)班第一小组一共13位同学,一定至少有( )名同学的生日在同一个月。为什么?
3.填空题
5÷4=1 …… 1 1+1=2
2
13÷12=1 …… 1 1+1=2
2
(3)张叔叔参加飞镖比赛,投了5镖,成绩是41环。张叔叔至少有一镖不低于( )环。为什么?
41÷5=8 …… 1 8+1=9
9
4.某学校有31名学生是6月份出生的,那么,其中至少有几名学生的生日是在同一天。为什么?
因为6月份有30天,相当于30个抽屉,31名学生相当于31个物体,31÷30=1……1,1+1=2,所以至少有2名学生的生日是同一天。
5.把8个梨子放进3个盘子里, 至少有3个梨子放入同一个盘子里,这句话对吗
8÷3=2(个)‥‥‥2(个)
2+1=3 (个)
答:以上说法是正确的
6.把10本书放进5个抽屉里, 总有一个抽屉里至少有几本书
10÷5=2(本)
答:总有一个抽屉里至少有2本书。
那么把15本书,放进4个抽屉里,总有一个抽屉里至少有几本书 快算算吧。
15÷4=3(本)……3(本)
3+1=4(本)
答:总有一个抽屉里至少有4本书。
乘风破浪会有时
直挂云帆济沧海
专题05:鸽 巢 问 题
期末专项考点复习
人教版·六年级下册
2023-2024学年
单元知识框架
4 ÷ 3=1……1 至少数 :1 + 1=2
5 ÷ 3=1……2 至少数 :1 + 1=2
6 ÷ 3=2 至少数 : 2
7 ÷ 3=2……1 至少数 :2 + 1=3
÷
=
商
……
余数
鸽子数
鸽巢数
至少数= 商+1
“至少数”的求法:
无余数
有余数
至少数= 商
www.islide.cc考点目录CONTENT“鸽巢原理”(一)“鸽巢原理”(二)应用“鸽巢原理”解决简单的实际问题考点01考点02考点03考点04考点05“鸽巢原理”(一)
/01
知识梳理
“鸽巢原理”(一):
把m个物体任意分放进n个鸽巢中(m和n是非0自然数,且m>n),那么一定有一个鸽巢中至少放进了2个物体。
举例:
把10个苹果放进9个抽屉,总有一个抽屉里至少放了2个苹果。这就是抽屉原理。
6只鸽子飞进5个鸽巢,总有一个鸽巢里至少飞进2只鸽子。这就是鸽巢原理。
典型例题
1、每个小组 6 名同学,6名同学中至少有几人在同一个季节里过生日?
题目分析:一年4个季节,所以 6 名同学中至少有2人在同一个季节里过生日。
6÷4=1……2
1+1=2
答:6名同学中至少有2人在同一个季节里过生日
典型例题
2.把7本书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书。为什么?
7÷3=2……1
跟踪练习
一副牌,取出大小王,还剩52张牌,5人每人随意抽一张,至少有几张牌是同花色的。
题目分析:一副扑克牌共54张,去掉两张王牌,剩下方块、红桃、梅花、黑桃四种花色各13张。我们把4种花色看成“4个鸽巢”,把5张扑克牌放进“4个鸽巢”中,必然有一个鸽巢至少放进2张扑克牌,即至少有2张牌是同花色的。
5÷4=1……1
1+1=2
答:即至少有2张牌是同花色的。
鸽巢原理”(二)
/02
知识梳理
“鸽巢原理”(二):
把多于kn个物体任意分进n个鸽巢中(k和n是非0自然数),那么一定有一个鸽巢中至少放进了(k+1)个物体。
典型例题
盒子里有同样大小的红球和蓝球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
题目分析:
只要摸出的球数比它们的颜色种数多1,就能保证有两个球同色。
2+1=3
答:至少要摸出3个球。
跟踪练习
一天晚上,小红正要从自已放袜子的抽屉里取袜子,突然灯熄了。她知道自己的抽屉里放有白色与黄色的袜子各6只。小红至少要摸出多少只袜子,才能保证拿出一双相同颜色的袜子?
题目分析:
只要摸出的袜子只数比它们的颜色种数多1,就能保证一双相同颜色的袜子。
2+1=3
答:至少要摸出3只袜子
应用“鸽巢原理”解决简单的实际问题
/03
知识梳理
1.如果有n( n是大于0的自然数)个“鸽笼”,要保证有一个“鸽笼”至少放进了2个物品,那么至少需要有n+1个物品。
2.如果有n( n是大于0的自然数)个“鸽笼”,要保证有一个“鸽笼”至少放进了(k+1)( k是大于0的自然数)个物品,那么至少需要有(kn+1)个物品。
3.(分放的物体总数-1)÷(其中一个鸽笼里至少有的物体个数-1)=a……b(b
4.利用“鸽巢问题”解决问题的思路和方法:
(1)分析题意,把实际问题转化成“鸽巢问题”,即弄清楚“鸽巢”(“鸽巢”是什么,有几个鸽巢)和分放的物体。
(2)设计“鸽巢”的具体形式。
(3)运用原理得出某个“鸽巢”中至少分放的物体个数,最终解决问题。
应用“鸽巢原理”解决实际问题的一般步骤:
①构造“鸽巢”,建立“数学模型”;
②把物体放入“鸽巢”,进行比较分析;
③说明理由,得出结论。
典型例题
从一副扑克牌(52张,没有大小王)中要抽出几张牌来,才能保证有一张是红桃?54张呢?
13×3+1=40
2+13×3+1=42
13
13
13
13
答:52张要抽出40张牌来,才能保证有一张是红桃
答:54张要抽出42张牌来,才能保证有一张是红桃
跟踪练习
希望小学篮球兴趣小组的同学中,最大的12岁,最小的6岁,最少从中挑选几名学生,就一定能找到两个学生年龄相同。
7+1=8
答:最少从中挑选8名学生
11只鸽子飞回4个鸽舍,至少有( )只鸽子要飞进同一个鸽舍。为什么?
11÷4=2……3
2+1=3
3
2.判断题
(1)11本书放进3个抽屉,至少有5本书要放进同一个抽屉里。( )
(2)17 只鸽子飞回5个鸽舍,至少有5个鸽子要飞进同一个鸽舍。( )
×
×
(1)5个人坐4把椅子,总有一把椅子上至少坐( )人。为什么?
(2)实验小学六(1)班第一小组一共13位同学,一定至少有( )名同学的生日在同一个月。为什么?
3.填空题
5÷4=1 …… 1 1+1=2
2
13÷12=1 …… 1 1+1=2
2
(3)张叔叔参加飞镖比赛,投了5镖,成绩是41环。张叔叔至少有一镖不低于( )环。为什么?
41÷5=8 …… 1 8+1=9
9
4.某学校有31名学生是6月份出生的,那么,其中至少有几名学生的生日是在同一天。为什么?
因为6月份有30天,相当于30个抽屉,31名学生相当于31个物体,31÷30=1……1,1+1=2,所以至少有2名学生的生日是同一天。
5.把8个梨子放进3个盘子里, 至少有3个梨子放入同一个盘子里,这句话对吗
8÷3=2(个)‥‥‥2(个)
2+1=3 (个)
答:以上说法是正确的
6.把10本书放进5个抽屉里, 总有一个抽屉里至少有几本书
10÷5=2(本)
答:总有一个抽屉里至少有2本书。
那么把15本书,放进4个抽屉里,总有一个抽屉里至少有几本书 快算算吧。
15÷4=3(本)……3(本)
3+1=4(本)
答:总有一个抽屉里至少有4本书。
乘风破浪会有时
直挂云帆济沧海
