沪教版九年级数学上册 第二十四章 相似三角形 单元综合复习题 (含解析)
文档属性
| 名称 | 沪教版九年级数学上册 第二十四章 相似三角形 单元综合复习题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 881.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-23 14:31:14 | ||
图片预览


文档简介
第二十四章 《相似三角形 》单元综合复习题
一、单选题
1.下列四组线段中,是成比例线段的是( )
A.1cm,2cm,3cm,4cm B.4cm,6cm,3cm.5cm
C.5cm,15cm,2cm.6cm D.3cm,4cm,2cm,5cm
2.下列命题中,正确的是( )
A.所有的正方形都相似 B.所有的菱形都相似
C.边长相等的两个菱形都相似 D.对角线相等的两个矩形都相似
3.如图, 中, 是 边上一点, 添加下列条件, 不能判定 的是( )
A. B. C. D.
4.下列关于向量的说法中,不正确的是( )
A.
B.如果,那么
C.是非零向量,是单位向量,那么
D.
5.如图,AB∥CD∥EF,则下列结论正确的是( )
A.= B.= C.= D.=
6.如图,在中,DE∥BC,若,则的值为( )
A. B. C. D.
7.如图,AD是△ABC的一条中线,G是△ABC的重心,过点G作EF∥BC,交AB,AC于点E,F.若BC=6,则EG的长为( )
A.2 B.3 C.3.5 D.4
8.如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC于点G,则下列结论中错误的是( )
A.△CGE∽△CBP B.△APD∽△PGD
C.△APG∽△BFP D.△PCF∽△BCP
9.如图,点G、F分别是的边、上的点,的延长线与的延长线相交于点A,交于点E,则下列结论错误的是( )
A. B. C. D.
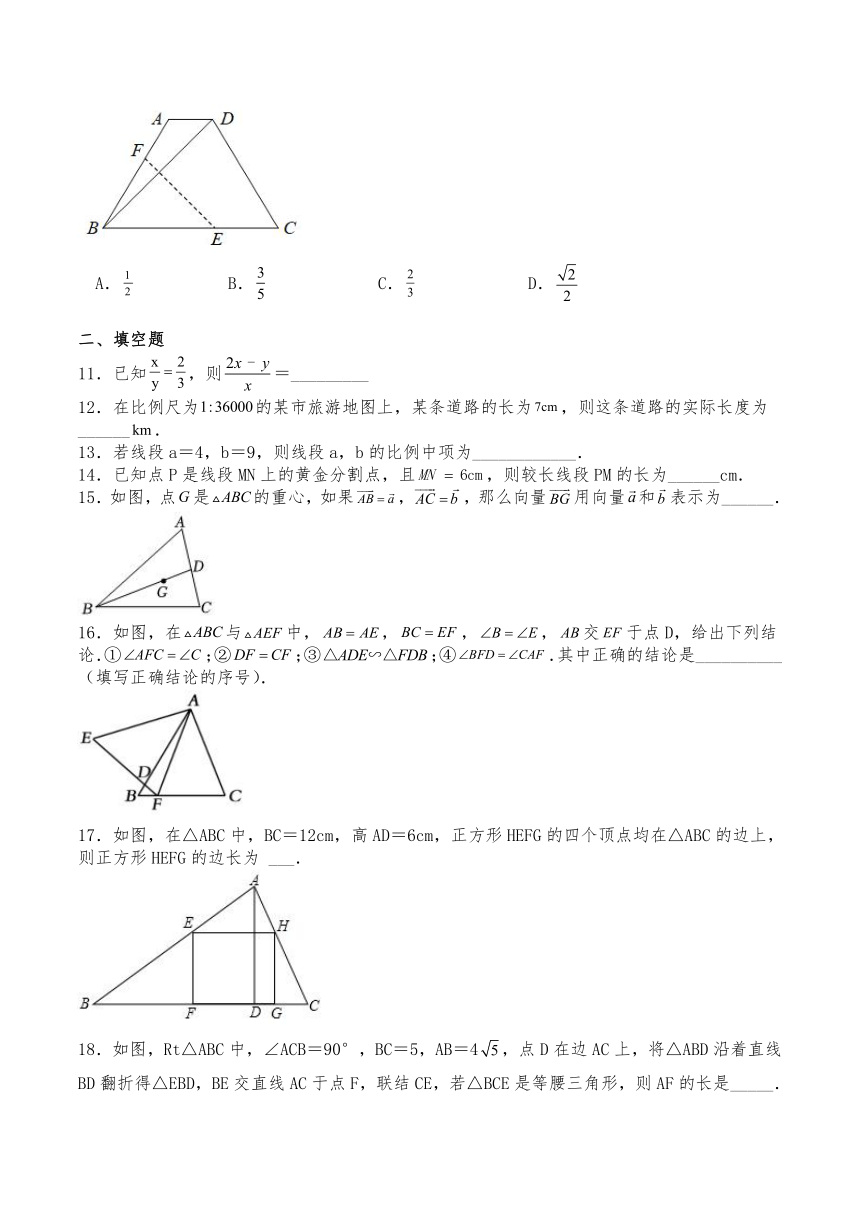
10.如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果,那么的值是( )
A. B. C. D.
二、填空题
11.已知,则=_________
12.在比例尺为的某市旅游地图上,某条道路的长为,则这条道路的实际长度为______.
13.若线段a=4,b=9,则线段a,b的比例中项为____________.
14.已知点P是线段MN上的黄金分割点,且,则较长线段PM的长为______cm.
15.如图,点是的重心,如果,,那么向量用向量和表示为______.
16.如图,在与中,,,,交于点D,给出下列结论.①;②;③;④.其中正确的结论是__________(填写正确结论的序号).
17.如图,在△ABC中,BC=12cm,高AD=6cm,正方形HEFG的四个顶点均在△ABC的边上,则正方形HEFG的边长为 ___.
18.如图,Rt△ABC中,∠ACB=90°,BC=5,AB=4,点D在边AC上,将△ABD沿着直线BD翻折得△EBD,BE交直线AC于点F,联结CE,若△BCE是等腰三角形,则AF的长是_____.
三、解答题
19.已知线段a、b、c满足且.
(1)求线段a、b、c的长;
(2)若线段x是线段a、b的比例中项(),求线段x的长.
20.如图,在中,点、分别在、上,,若,,,求AD的长.
21.如图,已知CD是Rt△ABC斜边AB上的中线,过点D作,过点C作CE⊥CD,两线相交于点E.
(1)求证:;
(2)若AC=8,BC=6,求DE的长.
22.如图,在平行四边形ABCD中,点E为边BC上一点,联结AE并延长交DC的延长线于点M,交BD于点G,过点G作GF∥BC交DC于点F,.
(1)若BD=20,求BG的长;
(2)求的值.
23.如图,在中,于点,于点,.
(1)求证:∽;
(2)若,,求的长.
24.已知:如图,在梯形中,,,,对角线、相交于点E,过点A作,交对角线BD于点F.
(1)求的值;
(2)设,,请用向量、表示向量.
25.如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE =AQ·AB求证:
(1)∠CAE=∠BAF;
(2)CF·FQ=AF·BQ
26.已知:如图,在四边形ABCD中,,点E在边BC上,且,作交线段AE于点F,连接BF.
(1)求证::
(2)如果,求证:.
27.如图,在等边ABC的AC,BC边上各取一点E,D,使AE=CD,AD,BE相交于点O.
(1)求证:AD=BE;
(2)若BO=6OE,求CD的长.
(3)在(2)的条件下,动点P在CE上从点C向终点E匀速运动,点Q在BC上,连结OP,PQ,满足∠OPQ=60°,记PC为x,DQ的长为y,求y关于x的函数表达式.
28.如图,在Rt△ABC中,点P为斜边BC上一动点,将△ABP沿直线AP折叠,使得点B的对应点为B',联结AB′,CB′,BB',PB',BB'与AP交于点E,PB'与AC交于点D.
(1)如图1,若AP=PC,BC=6,cos∠ABC=,求CB'的长;
(2)如图2,若AB=AC,BP=3PC,求的值.
答案
一、单选题
1.C
【分析】如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.对选项一一分析,排除错误答案.
【解析】解:A、1×4≠2×3,故选项错误,该选项不符合题意;
B、3×6≠5×4,故选项错误,该选项不符合题意;
C、2×15=5×6,故选项正确,该选项符合题意;
D、2×5≠3×4,故选项错误,该选项不符合题意.
故选:C.
2.A
【分析】两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形,根据相似多边形的定义逐项判断即可.
【解析】解:A.所有的正方形都相似,故选项正确,符合题意;
B.菱形的边成比例,但角不一定相等,故选项错误,不符合题意;
C.边长相等的两个菱形都不一定相似,故选项错误,不符合题意;
D.对角线相等的两个矩形边不一定成比例,所以不一定相似,故选项错误,不符合题意;
故选:A.
3.D
【分析】根据三角形相似的判定定理逐一分析判断即可.
【解析】解:A、∵,
∴
所以选项A不符合题意;
B、∵,
∴
所以选项B不符合题意;
C、∵,
∴
所以选项C不符合题意;
D、,对应边成比例,但是不确定是否与相等,所以不能判定,所以选项D符合题意.
故选:D
4.C
【分析】根据平面向量的定义(在平面中既有大小又有方向的量称为向量)与运算法则依次进行判断即可得出选项.
【解析】解:A、,本选项正确,不符合题意;
B、如果,则,选项正确,不符合题意;
C、等号左边为向量,右边为向量模长,选项错误,符合题意;
D、,本选项正确,不符合题意.
故选:C.
5.B
【分析】根据平行线分线段成比例定理,对各项进行分析即可.
【解析】解:∵AB∥CD∥EF,
∴=,=,
∴选项A、C、D不正确,选项B正确;
故选:B.
6.D
【分析】根据相似三角形的判定与性质可得,由此即可得出答案.
【解析】解:,
,
,
,
,
,
,
故选:D.
7.A
【分析】根据AD是中线,得到,由G为△ABC的重心,可以得到,有EF∥BC,可以证明△AEG∽△ABD,得到,由此求解即可.
【解析】解:∵AD是中线,
∴,
∵G为△ABC的重心,
∴,
∵EF∥BC,
∴△AEG∽△ABD,
∴,
∴,
故选A.
8.A
【分析】根据∠CPD=∠A=∠B,∠D=∠D,∠C=∠C即可得到△APD∽△PGD,△PCF∽△BCP,再根据∠APG=∠C+∠P,∠BFP=∠C+∠CPD,可以得到∠APG=∠BFP,即可证明△APG∽△BFP,由此即可求解.
【解析】解:∵∠CPD=∠A=∠B,∠D=∠D,∠C=∠C
∴△APD∽△PGD,△PCF∽△BCP
故B、D选项不符合题意,
∵∠APG=∠C+∠P,∠BFP=∠C+∠CPD,
∴∠APG=∠BFP,
∴△APG∽△BFP,故C选项不符合题意,
对于A选项不能得到两个三角形相似,
故选A.
9.C
【分析】利用平行线分线段成比例定理即可得到答案.
【解析】解:∵交GA于点E,
,,,,
所以,A,B,D正确,
故选:C.
10.B
【解析】解:∵EF是点B、D的对称轴,
∴△BFE≌△DFE,
∴DE=BE.
∵在△BDE中,DE=BE,∠DBE=45°,
∴∠BDE=∠DBE=45°,
∴∠DEB=90°,
∴DE⊥BC.
在等腰梯形ABCD中,
∵=,
∴设AD=1,BC=4,过A作AG⊥BC于G,
∴四边形AGED是矩形,
∴GE=AD=1,
∵Rt△ABG≌Rt△DCE,
∴BG=EC=1.5,
∴AG=DE=BE=2.5,
∴AB=CD==,
∵∠ABC=∠C=∠FDE,∠CDE+∠C=90°,
∴∠FDE+∠CDE=90°,
∴∠FDB+∠BDC+∠FDB=∠FDB+∠DFE=90°,
∴∠BDC=∠DFE,
∵∠DEF=∠DBC=45°,
∴△BDC∽△DEF,
∴,
∴DF=,
∴BF=,
∴AF=AB﹣BF=,
∴=.
故选B.
二、填空题
11.
【分析】依据比例的性质,即可得到y=x,再代入分式计算化简即可.
【解析】解:∵,
∴y=x,
∴ ,
故答案为: .
12.
【分析】根据比例尺图上距离:实际距离,依题意列比例式直接求解即可.
【解析】解:设这条道路的实际长度为,则:
,
解得.
故答案是:.
13.6
【分析】由四条线段a,x,x,b成比例,根据成比例线段的定义解答即可.
【解析】解:设线段a,b的比例中项为c,c>0,
根据比例中项原则:c2=ab,
∴c2=4×9,
∴c=6
故答案:6.
14.
【分析】根据黄金分割比为,根据PM为较长线段则,
【解析】解:∵点P是线段MN上的黄金分割点,且,
∴长线段PM的长为.
故答案为:
15.
【分析】由是的重心,推出,,求出,可得结论.
【解析】解:∵G是的重心,
∴,,
∵,
∴,
故答案为:.
16.①③④
【分析】根据SAS推出△AEF≌△ABC,推出AF=AC,根据等边对等角推出即可①正确;不正确,采用反证法,假设,可以证明△ACF≌△AFD,即可证明∠DAF=∠CAF,由题意无法得出此结论,判断②错误;根据∠E=∠B,∠EDA=∠BDF,推出△ADE∽△FDB即可判断③正确;根据△AEF≌△ABC,得出∠EAF=∠BAC,求出∠EAD=∠CAF,根据相似三角形性质得出∠BFD=∠EAD=∠CAF,即可判断④正确
【解析】解:在△AEF和△ABC中
∵,
∴△AEF≌△ABC(SAS),
∴AF=AC,
∴∠AFC=∠C,
∴①正确;
不正确,理由是:假设,
∵△AEF≌△ABC
∴∠AFD=∠C,AF=AC,
∴△ACF≌△AFD,
∴∠DAF=∠FAC,
原题中无AF为∠BAC平分线这一条件,
∴②错误;
∵∠E=∠B,∠EDA=∠BDF,
∴△ADE∽△FDB,
∴③正确;
∵△AEF≌△ABC,
∴∠EAF=∠BAC,
∴∠EAF﹣∠DAF=∠BAC﹣∠DAF,
∴∠EAD=∠CAF,
∵△ADE∽△FBD,
∴∠BFD=∠EAD=∠CAF,
∴④正确;
故答案为:①③④
17.4 cm
【分析】设正方形的边长为x cm,然后根据相似三角形的性质列出比例式即可求出答案.
【解析】解:设正方形的边长为xcm,
∴AP=AD﹣PD=6﹣x,
∵EH∥BC,
∴△AEH∽△ABC,
∴,
∴=,
解得:x=4,
故答案为:4cm
18.
【分析】根据题意作图如下,过作的垂线,交于,由勾股定理求得,根据翻折的性质,可得:,
若△BCE是等腰三角形,则,勾股定理求出,在证明,求出,根据,即可求出.
【解析】解:在边AC上,将△ABD沿着直线BD翻折得△EBD,BE交直线AC于点F,联结CE,根据题意作图如下,过作的垂线,交于,
在中,
,
根据翻折的性质,可得:,
当点D在边AC之间上动时,且BE交直线AC于点F,
故,
若△BCE是等腰三角形,
则,
根据等腰三角形的三线合一的性质知,
点为的中点,
,
,
,
,
,
,
,
即,
解得:,
,
故答案是:.
三、解答题
19.
(1)
解:设,则,,,
,
,
解得,
则,,.
(2)
解:线段是线段、的比例中项,且,,
,
解得或(舍去),
经检验,是所列分式方程的解,
即线段的长为.
20.解:∵DE∥BC,
∴,
设AD=x,则,
∴,
解得:x=4或﹣4(舍去),
即AD=4.
21.解(1)由题意:
∵CE⊥CD,
∴,
又∵,
∴∠CDE=∠ACD,
∵在中,CD是AB边上的中线,
∴CD=AD,
∴∠ACD=∠CAD,
∴∠CDE=∠CAD,
∴.
(2)∵AC=8,BC=6,
∴利用勾股定理得:
∵在中,CD是AB边上的中线,
∴CD=5,
∵
∴AB∶DE=AC∶CD,即10∶DE=8∶5,
∴DE=.
22.(1) ∵GF∥BC,
∴,
∵BD=20,,
∴ ;
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴,
∴,
∴,
∴.
23.解:(1)证明:点于点,于点,
,
,
,
;
(2)解:,
,
,
,,
,
,
,
,
,
,
.
24.
(1)
解:,
,
,
,
,
设,则,,
,
(2)
解:,,,
,,
,,
,
,
,
,
.
25.
(1)
证明:∵AB=AC,
∴∠B=∠C,
∵CF=BE,
∴CE=BF,
在△ACE和△ABF中,,
∴△ACE≌△ABF(SAS),
∴∠CAE=∠BAF;
(2)
证明:∵△ACE≌△ABF,
∴AE=AF,∠CAE=∠BAF,
∵AE =AQ·AB,AC=AB,
∴,即,
∴△ACE∽△AFQ,
∴∠AEC=∠AQF,
∴∠AEF=∠BQF,
∵AE=AF,
∴∠AEF=∠AFE,
∴∠BQF=∠AFE,
∵∠B=∠C,
∴△CAF∽△BFQ,
∴,即CF·FQ=AF·BQ.
26.
(1)
∵,∴
∵
∴
∵
∴
∴
∵
∴四边形AFCD是平行四边形
∴
∴
∴
(2)
∵
∴
在中,
∴
∴
∵,
在与中
∴
∴
∵
∴
27.解:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°,
又∵AE=CD,
∴△BAE≌△ACD(SAS),
∴AD=BE;
(2)由(1)得△BAE≌△ACD,
∴∠ABO=∠CAD,AD=BE
∴∠BAO+∠ABO=∠AOE=∠EAO+∠BAO=∠BAC=∠C=60°,
又∵∠CAD=∠OAE,
∴△CAD∽△OAE,
∴,
∵,
∴,
∴,
∵CD=AE,
∴,
∴CD=2;
(3)如图所示,过点E作EF⊥AB于F,过点O作OG∥AB交AC于G,
∵∠FAG=60°,∠AEF=30°,
∴,
∴,
∴,
∴,
∵OG∥AB,
∴△OGE∽△BAE,∠OGE=∠BAC=60°
∴,
∴,,
∴,
∵∠AOE=60°,
∴∠OEP=∠AOE+∠OAE=60°+∠OAE,
∵∠EPQ=∠C+∠PQC=∠OPQ+∠OPE,∠C=∠OPQ=60°,
∴∠OPE=∠CQP,
∴△PQC∽△OPG,
∴,
∵,
∴,
∴,
∵,
∴.
28.
(1)
解:(1)∵AP=PC,
∴∠PCA=∠PAC,
∵∠BAC=90°,
∴∠ACP=90°﹣∠PBA,∠PAC=90°﹣∠PAB,
∴∠PAB=∠PBA,
∴PA=PB=PC,
∴点P是BC的中点,
∵BC=6,cos∠ABC= ,
∴PC=PB=PA=3,AB=BC×cos∠ABC=6× =2,
由折叠得,PB'=PB=PC,AP⊥B'B,∠APB=∠APB',
设AE=x,则PE=PA﹣AE=3﹣x,
在Rt△PBE中,BE2=PB2﹣PE2,
在Rt△ABE中,BE2=AB2﹣AE2,
∴AB2﹣AE2=PB2﹣PE2,即22﹣x2=32﹣(3﹣x)2,
解得:x= ,
∴PE= ,
过点P作PH⊥B'C于点H,则∠PHC=∠BEP=90°,
∵PB'=PC,
∴点H是B'C的中点,∠CPH=∠B'PH,
∵∠APB=∠APB',∠APB+∠APB'+∠CPH+∠B'PH=180°,
∴∠CPH+∠APB=90°,
∵∠APB+∠PBE=90°,
∴∠CPH=∠PBE,
又∵BP=PC,∠PHC=∠BEP,
∴△CPH≌△PBE(AAS),
∴CH=PE= ,
∴B'H= ,
∴B'C=CH+B'H= = .
(2)
设AB=AC=4a,则BC=,
∵BP=3CP,
∴CP= ,BP=,
由折叠得,∠AB'P=∠ABP=45°,PB'=PB=,AB'=AB=4a,
∴∠AB'D=∠PCD,
∵∠B'DA=∠CDP,
∴△B'DA∽△CDP,
∴ ,
设CD=n,PD=m,则AD=4a﹣n,B'D=,
∴ ,
解得:m=,n= ,
∴B'D=,AD=,
∴ .
一、单选题
1.下列四组线段中,是成比例线段的是( )
A.1cm,2cm,3cm,4cm B.4cm,6cm,3cm.5cm
C.5cm,15cm,2cm.6cm D.3cm,4cm,2cm,5cm
2.下列命题中,正确的是( )
A.所有的正方形都相似 B.所有的菱形都相似
C.边长相等的两个菱形都相似 D.对角线相等的两个矩形都相似
3.如图, 中, 是 边上一点, 添加下列条件, 不能判定 的是( )
A. B. C. D.
4.下列关于向量的说法中,不正确的是( )
A.
B.如果,那么
C.是非零向量,是单位向量,那么
D.
5.如图,AB∥CD∥EF,则下列结论正确的是( )
A.= B.= C.= D.=
6.如图,在中,DE∥BC,若,则的值为( )
A. B. C. D.
7.如图,AD是△ABC的一条中线,G是△ABC的重心,过点G作EF∥BC,交AB,AC于点E,F.若BC=6,则EG的长为( )
A.2 B.3 C.3.5 D.4
8.如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC于点G,则下列结论中错误的是( )
A.△CGE∽△CBP B.△APD∽△PGD
C.△APG∽△BFP D.△PCF∽△BCP
9.如图,点G、F分别是的边、上的点,的延长线与的延长线相交于点A,交于点E,则下列结论错误的是( )
A. B. C. D.
10.如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果,那么的值是( )
A. B. C. D.
二、填空题
11.已知,则=_________
12.在比例尺为的某市旅游地图上,某条道路的长为,则这条道路的实际长度为______.
13.若线段a=4,b=9,则线段a,b的比例中项为____________.
14.已知点P是线段MN上的黄金分割点,且,则较长线段PM的长为______cm.
15.如图,点是的重心,如果,,那么向量用向量和表示为______.
16.如图,在与中,,,,交于点D,给出下列结论.①;②;③;④.其中正确的结论是__________(填写正确结论的序号).
17.如图,在△ABC中,BC=12cm,高AD=6cm,正方形HEFG的四个顶点均在△ABC的边上,则正方形HEFG的边长为 ___.
18.如图,Rt△ABC中,∠ACB=90°,BC=5,AB=4,点D在边AC上,将△ABD沿着直线BD翻折得△EBD,BE交直线AC于点F,联结CE,若△BCE是等腰三角形,则AF的长是_____.
三、解答题
19.已知线段a、b、c满足且.
(1)求线段a、b、c的长;
(2)若线段x是线段a、b的比例中项(),求线段x的长.
20.如图,在中,点、分别在、上,,若,,,求AD的长.
21.如图,已知CD是Rt△ABC斜边AB上的中线,过点D作,过点C作CE⊥CD,两线相交于点E.
(1)求证:;
(2)若AC=8,BC=6,求DE的长.
22.如图,在平行四边形ABCD中,点E为边BC上一点,联结AE并延长交DC的延长线于点M,交BD于点G,过点G作GF∥BC交DC于点F,.
(1)若BD=20,求BG的长;
(2)求的值.
23.如图,在中,于点,于点,.
(1)求证:∽;
(2)若,,求的长.
24.已知:如图,在梯形中,,,,对角线、相交于点E,过点A作,交对角线BD于点F.
(1)求的值;
(2)设,,请用向量、表示向量.
25.如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE =AQ·AB求证:
(1)∠CAE=∠BAF;
(2)CF·FQ=AF·BQ
26.已知:如图,在四边形ABCD中,,点E在边BC上,且,作交线段AE于点F,连接BF.
(1)求证::
(2)如果,求证:.
27.如图,在等边ABC的AC,BC边上各取一点E,D,使AE=CD,AD,BE相交于点O.
(1)求证:AD=BE;
(2)若BO=6OE,求CD的长.
(3)在(2)的条件下,动点P在CE上从点C向终点E匀速运动,点Q在BC上,连结OP,PQ,满足∠OPQ=60°,记PC为x,DQ的长为y,求y关于x的函数表达式.
28.如图,在Rt△ABC中,点P为斜边BC上一动点,将△ABP沿直线AP折叠,使得点B的对应点为B',联结AB′,CB′,BB',PB',BB'与AP交于点E,PB'与AC交于点D.
(1)如图1,若AP=PC,BC=6,cos∠ABC=,求CB'的长;
(2)如图2,若AB=AC,BP=3PC,求的值.
答案
一、单选题
1.C
【分析】如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.对选项一一分析,排除错误答案.
【解析】解:A、1×4≠2×3,故选项错误,该选项不符合题意;
B、3×6≠5×4,故选项错误,该选项不符合题意;
C、2×15=5×6,故选项正确,该选项符合题意;
D、2×5≠3×4,故选项错误,该选项不符合题意.
故选:C.
2.A
【分析】两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形,根据相似多边形的定义逐项判断即可.
【解析】解:A.所有的正方形都相似,故选项正确,符合题意;
B.菱形的边成比例,但角不一定相等,故选项错误,不符合题意;
C.边长相等的两个菱形都不一定相似,故选项错误,不符合题意;
D.对角线相等的两个矩形边不一定成比例,所以不一定相似,故选项错误,不符合题意;
故选:A.
3.D
【分析】根据三角形相似的判定定理逐一分析判断即可.
【解析】解:A、∵,
∴
所以选项A不符合题意;
B、∵,
∴
所以选项B不符合题意;
C、∵,
∴
所以选项C不符合题意;
D、,对应边成比例,但是不确定是否与相等,所以不能判定,所以选项D符合题意.
故选:D
4.C
【分析】根据平面向量的定义(在平面中既有大小又有方向的量称为向量)与运算法则依次进行判断即可得出选项.
【解析】解:A、,本选项正确,不符合题意;
B、如果,则,选项正确,不符合题意;
C、等号左边为向量,右边为向量模长,选项错误,符合题意;
D、,本选项正确,不符合题意.
故选:C.
5.B
【分析】根据平行线分线段成比例定理,对各项进行分析即可.
【解析】解:∵AB∥CD∥EF,
∴=,=,
∴选项A、C、D不正确,选项B正确;
故选:B.
6.D
【分析】根据相似三角形的判定与性质可得,由此即可得出答案.
【解析】解:,
,
,
,
,
,
,
故选:D.
7.A
【分析】根据AD是中线,得到,由G为△ABC的重心,可以得到,有EF∥BC,可以证明△AEG∽△ABD,得到,由此求解即可.
【解析】解:∵AD是中线,
∴,
∵G为△ABC的重心,
∴,
∵EF∥BC,
∴△AEG∽△ABD,
∴,
∴,
故选A.
8.A
【分析】根据∠CPD=∠A=∠B,∠D=∠D,∠C=∠C即可得到△APD∽△PGD,△PCF∽△BCP,再根据∠APG=∠C+∠P,∠BFP=∠C+∠CPD,可以得到∠APG=∠BFP,即可证明△APG∽△BFP,由此即可求解.
【解析】解:∵∠CPD=∠A=∠B,∠D=∠D,∠C=∠C
∴△APD∽△PGD,△PCF∽△BCP
故B、D选项不符合题意,
∵∠APG=∠C+∠P,∠BFP=∠C+∠CPD,
∴∠APG=∠BFP,
∴△APG∽△BFP,故C选项不符合题意,
对于A选项不能得到两个三角形相似,
故选A.
9.C
【分析】利用平行线分线段成比例定理即可得到答案.
【解析】解:∵交GA于点E,
,,,,
所以,A,B,D正确,
故选:C.
10.B
【解析】解:∵EF是点B、D的对称轴,
∴△BFE≌△DFE,
∴DE=BE.
∵在△BDE中,DE=BE,∠DBE=45°,
∴∠BDE=∠DBE=45°,
∴∠DEB=90°,
∴DE⊥BC.
在等腰梯形ABCD中,
∵=,
∴设AD=1,BC=4,过A作AG⊥BC于G,
∴四边形AGED是矩形,
∴GE=AD=1,
∵Rt△ABG≌Rt△DCE,
∴BG=EC=1.5,
∴AG=DE=BE=2.5,
∴AB=CD==,
∵∠ABC=∠C=∠FDE,∠CDE+∠C=90°,
∴∠FDE+∠CDE=90°,
∴∠FDB+∠BDC+∠FDB=∠FDB+∠DFE=90°,
∴∠BDC=∠DFE,
∵∠DEF=∠DBC=45°,
∴△BDC∽△DEF,
∴,
∴DF=,
∴BF=,
∴AF=AB﹣BF=,
∴=.
故选B.
二、填空题
11.
【分析】依据比例的性质,即可得到y=x,再代入分式计算化简即可.
【解析】解:∵,
∴y=x,
∴ ,
故答案为: .
12.
【分析】根据比例尺图上距离:实际距离,依题意列比例式直接求解即可.
【解析】解:设这条道路的实际长度为,则:
,
解得.
故答案是:.
13.6
【分析】由四条线段a,x,x,b成比例,根据成比例线段的定义解答即可.
【解析】解:设线段a,b的比例中项为c,c>0,
根据比例中项原则:c2=ab,
∴c2=4×9,
∴c=6
故答案:6.
14.
【分析】根据黄金分割比为,根据PM为较长线段则,
【解析】解:∵点P是线段MN上的黄金分割点,且,
∴长线段PM的长为.
故答案为:
15.
【分析】由是的重心,推出,,求出,可得结论.
【解析】解:∵G是的重心,
∴,,
∵,
∴,
故答案为:.
16.①③④
【分析】根据SAS推出△AEF≌△ABC,推出AF=AC,根据等边对等角推出即可①正确;不正确,采用反证法,假设,可以证明△ACF≌△AFD,即可证明∠DAF=∠CAF,由题意无法得出此结论,判断②错误;根据∠E=∠B,∠EDA=∠BDF,推出△ADE∽△FDB即可判断③正确;根据△AEF≌△ABC,得出∠EAF=∠BAC,求出∠EAD=∠CAF,根据相似三角形性质得出∠BFD=∠EAD=∠CAF,即可判断④正确
【解析】解:在△AEF和△ABC中
∵,
∴△AEF≌△ABC(SAS),
∴AF=AC,
∴∠AFC=∠C,
∴①正确;
不正确,理由是:假设,
∵△AEF≌△ABC
∴∠AFD=∠C,AF=AC,
∴△ACF≌△AFD,
∴∠DAF=∠FAC,
原题中无AF为∠BAC平分线这一条件,
∴②错误;
∵∠E=∠B,∠EDA=∠BDF,
∴△ADE∽△FDB,
∴③正确;
∵△AEF≌△ABC,
∴∠EAF=∠BAC,
∴∠EAF﹣∠DAF=∠BAC﹣∠DAF,
∴∠EAD=∠CAF,
∵△ADE∽△FBD,
∴∠BFD=∠EAD=∠CAF,
∴④正确;
故答案为:①③④
17.4 cm
【分析】设正方形的边长为x cm,然后根据相似三角形的性质列出比例式即可求出答案.
【解析】解:设正方形的边长为xcm,
∴AP=AD﹣PD=6﹣x,
∵EH∥BC,
∴△AEH∽△ABC,
∴,
∴=,
解得:x=4,
故答案为:4cm
18.
【分析】根据题意作图如下,过作的垂线,交于,由勾股定理求得,根据翻折的性质,可得:,
若△BCE是等腰三角形,则,勾股定理求出,在证明,求出,根据,即可求出.
【解析】解:在边AC上,将△ABD沿着直线BD翻折得△EBD,BE交直线AC于点F,联结CE,根据题意作图如下,过作的垂线,交于,
在中,
,
根据翻折的性质,可得:,
当点D在边AC之间上动时,且BE交直线AC于点F,
故,
若△BCE是等腰三角形,
则,
根据等腰三角形的三线合一的性质知,
点为的中点,
,
,
,
,
,
,
,
即,
解得:,
,
故答案是:.
三、解答题
19.
(1)
解:设,则,,,
,
,
解得,
则,,.
(2)
解:线段是线段、的比例中项,且,,
,
解得或(舍去),
经检验,是所列分式方程的解,
即线段的长为.
20.解:∵DE∥BC,
∴,
设AD=x,则,
∴,
解得:x=4或﹣4(舍去),
即AD=4.
21.解(1)由题意:
∵CE⊥CD,
∴,
又∵,
∴∠CDE=∠ACD,
∵在中,CD是AB边上的中线,
∴CD=AD,
∴∠ACD=∠CAD,
∴∠CDE=∠CAD,
∴.
(2)∵AC=8,BC=6,
∴利用勾股定理得:
∵在中,CD是AB边上的中线,
∴CD=5,
∵
∴AB∶DE=AC∶CD,即10∶DE=8∶5,
∴DE=.
22.(1) ∵GF∥BC,
∴,
∵BD=20,,
∴ ;
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴,
∴,
∴,
∴.
23.解:(1)证明:点于点,于点,
,
,
,
;
(2)解:,
,
,
,,
,
,
,
,
,
,
.
24.
(1)
解:,
,
,
,
,
设,则,,
,
(2)
解:,,,
,,
,,
,
,
,
,
.
25.
(1)
证明:∵AB=AC,
∴∠B=∠C,
∵CF=BE,
∴CE=BF,
在△ACE和△ABF中,,
∴△ACE≌△ABF(SAS),
∴∠CAE=∠BAF;
(2)
证明:∵△ACE≌△ABF,
∴AE=AF,∠CAE=∠BAF,
∵AE =AQ·AB,AC=AB,
∴,即,
∴△ACE∽△AFQ,
∴∠AEC=∠AQF,
∴∠AEF=∠BQF,
∵AE=AF,
∴∠AEF=∠AFE,
∴∠BQF=∠AFE,
∵∠B=∠C,
∴△CAF∽△BFQ,
∴,即CF·FQ=AF·BQ.
26.
(1)
∵,∴
∵
∴
∵
∴
∴
∵
∴四边形AFCD是平行四边形
∴
∴
∴
(2)
∵
∴
在中,
∴
∴
∵,
在与中
∴
∴
∵
∴
27.解:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°,
又∵AE=CD,
∴△BAE≌△ACD(SAS),
∴AD=BE;
(2)由(1)得△BAE≌△ACD,
∴∠ABO=∠CAD,AD=BE
∴∠BAO+∠ABO=∠AOE=∠EAO+∠BAO=∠BAC=∠C=60°,
又∵∠CAD=∠OAE,
∴△CAD∽△OAE,
∴,
∵,
∴,
∴,
∵CD=AE,
∴,
∴CD=2;
(3)如图所示,过点E作EF⊥AB于F,过点O作OG∥AB交AC于G,
∵∠FAG=60°,∠AEF=30°,
∴,
∴,
∴,
∴,
∵OG∥AB,
∴△OGE∽△BAE,∠OGE=∠BAC=60°
∴,
∴,,
∴,
∵∠AOE=60°,
∴∠OEP=∠AOE+∠OAE=60°+∠OAE,
∵∠EPQ=∠C+∠PQC=∠OPQ+∠OPE,∠C=∠OPQ=60°,
∴∠OPE=∠CQP,
∴△PQC∽△OPG,
∴,
∵,
∴,
∴,
∵,
∴.
28.
(1)
解:(1)∵AP=PC,
∴∠PCA=∠PAC,
∵∠BAC=90°,
∴∠ACP=90°﹣∠PBA,∠PAC=90°﹣∠PAB,
∴∠PAB=∠PBA,
∴PA=PB=PC,
∴点P是BC的中点,
∵BC=6,cos∠ABC= ,
∴PC=PB=PA=3,AB=BC×cos∠ABC=6× =2,
由折叠得,PB'=PB=PC,AP⊥B'B,∠APB=∠APB',
设AE=x,则PE=PA﹣AE=3﹣x,
在Rt△PBE中,BE2=PB2﹣PE2,
在Rt△ABE中,BE2=AB2﹣AE2,
∴AB2﹣AE2=PB2﹣PE2,即22﹣x2=32﹣(3﹣x)2,
解得:x= ,
∴PE= ,
过点P作PH⊥B'C于点H,则∠PHC=∠BEP=90°,
∵PB'=PC,
∴点H是B'C的中点,∠CPH=∠B'PH,
∵∠APB=∠APB',∠APB+∠APB'+∠CPH+∠B'PH=180°,
∴∠CPH+∠APB=90°,
∵∠APB+∠PBE=90°,
∴∠CPH=∠PBE,
又∵BP=PC,∠PHC=∠BEP,
∴△CPH≌△PBE(AAS),
∴CH=PE= ,
∴B'H= ,
∴B'C=CH+B'H= = .
(2)
设AB=AC=4a,则BC=,
∵BP=3CP,
∴CP= ,BP=,
由折叠得,∠AB'P=∠ABP=45°,PB'=PB=,AB'=AB=4a,
∴∠AB'D=∠PCD,
∵∠B'DA=∠CDP,
∴△B'DA∽△CDP,
∴ ,
设CD=n,PD=m,则AD=4a﹣n,B'D=,
∴ ,
解得:m=,n= ,
∴B'D=,AD=,
∴ .
