初中数学人教版九年级下册28.1锐角三角函数说课课件(32张PPT)
文档属性
| 名称 | 初中数学人教版九年级下册28.1锐角三角函数说课课件(32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 621.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-23 00:00:00 | ||
图片预览




文档简介
(共32张PPT)
锐角三角函数
教材分析
教法学法
教学过程
内容处理
学情分析
锐角三角函数
锐角三角函数
教材分析
地位作用
重点难点
教学目标
教材分析
教法学法
教学过程
反思评价
学情分析
知识目标:理解锐角三角函数定义和直角三 角形的解法
能力目标:培养运用图形分析问题的能力
情感目标:通过主动探究,合作交流,感受探索的乐趣和成功的体验,体会数学的合理性和严谨性。
起着承前启后的作用
重点:锐角三角函数定义和直角三角形的解法
难点:正确理解锐角三角函数的概念
锐角三角函数
学情分析
学习特点
已有基础
学习了相似三角形与勾股定理等知识的基础上
学生更侧重背公式,忽视对公式推导和概念的理解
教材分析
教法学法
教学过程
学情分析
反思评价
锐角三角函数
教法学法
学法
教法
讲授法、讨论法相结合
教师要指导学生课前预习,并且思考如下问题,本节课与以前学过的知识有什么联系,什么区别,体现出什么思想方法?
教材分析
教法学法
教学过程
学情分析
反思评价
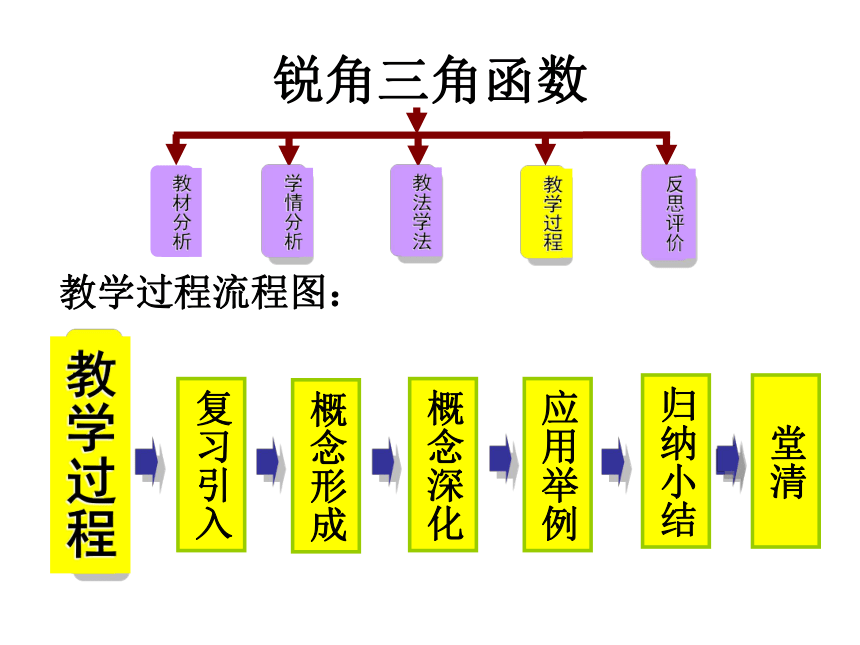
教学过程流程图:
教学过程
教材分析
教法学法
教学过程
学情分析
反思评价
锐角三角函数
复习引入
概念形成
概念深化
堂清
应用举例
归纳小结
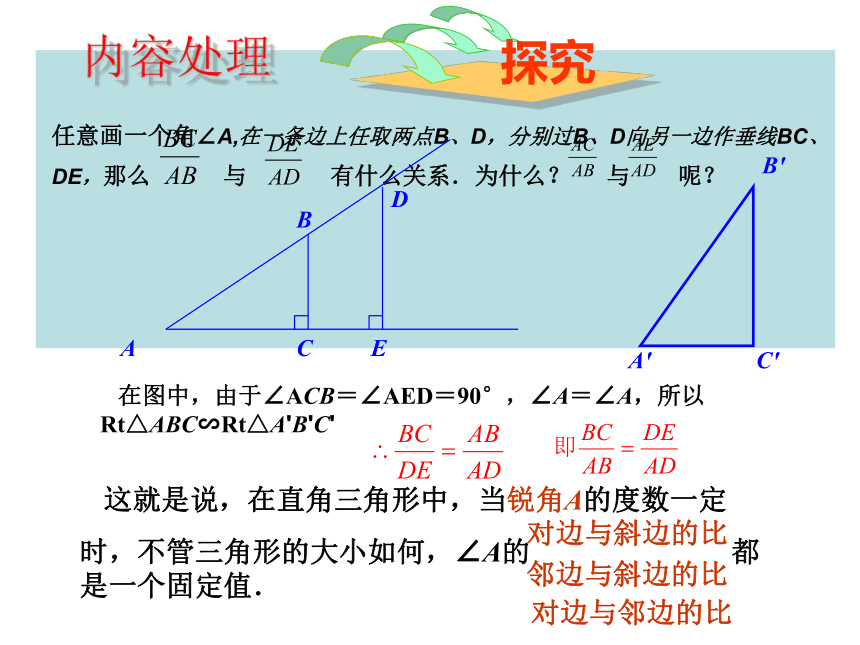
在图中,由于∠ACB=∠AED=90°,∠A=∠A,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角A的度数一定
时,不管三角形的大小如何,∠A的 都是一个固定值.
任意画一个角∠A,在一条边上任取两点B、D,分别过B、D向另一边作垂线BC、DE,那么 与 有什么关系.为什么? 与 呢?
探究
A
B
C
E
D
A'
B'
C'
对边与邻边的比
邻边与斜边的比
对边与斜边的比
内容处理
让学生体会定义的发生发展过程,从而理解,突破难点。
设计意图
=
a
c
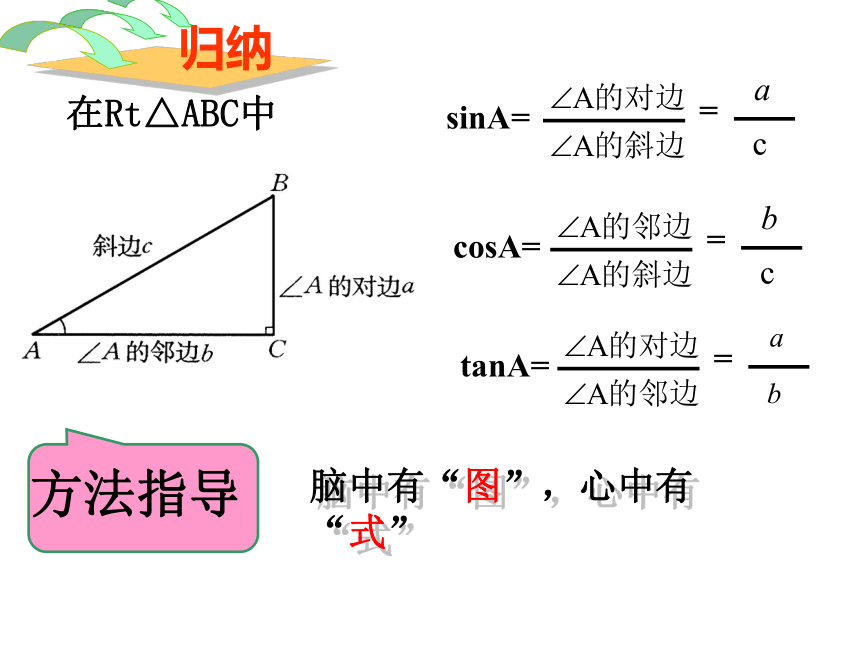
sinA=
在Rt△ABC中
=
b
c
cosA=
=
a
b
tanA=
归纳
方法指导
脑中有“图”,心中有“式”
α
对边
邻边
斜边
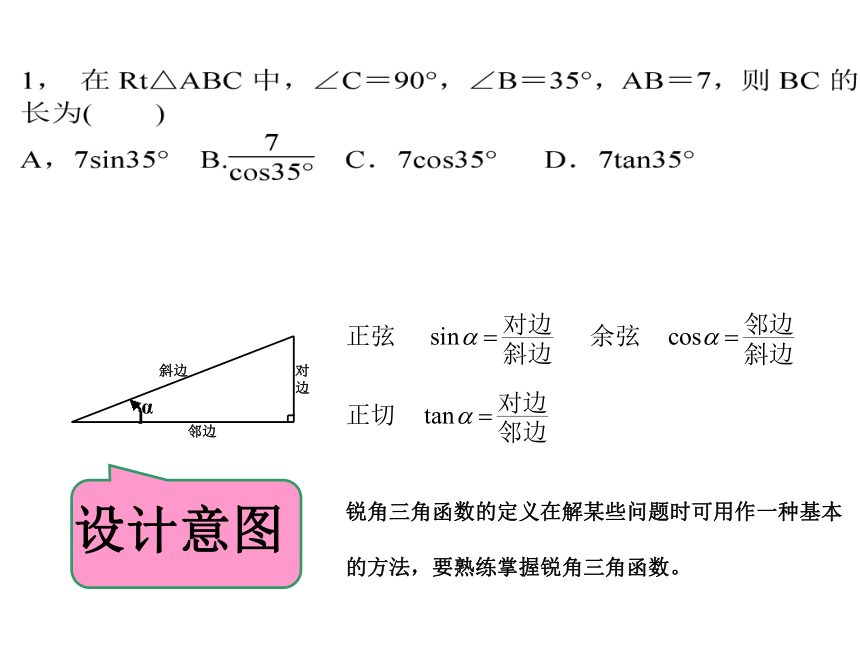
锐角三角函数的定义在解某些问题时可用作一种基本的方法,要熟练掌握锐角三角函数。
设计意图
定义中应该注意的几个问题:
1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA、 cosA、tanA是一个比值(数值)。
3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
A
B
C
30°
x
2x
sin30°=
cos30°=
tan30°=
2
3
300角的各类三角函数值的探索
在直角三角形中,如果一个锐角等于300,那么它所对的直角边等于斜边的一半。
(4)sin450,sin600等于多少
(5)cos450,cos600等于多少
(6)tan450,tan600等于多少
┌
┌
300
600
450
450
小组间讨论
此处做法简单,思想重要。将形与数结合了起来,体现出了一种重要的思想方法——数形结合法。
设计意图
三角函数
锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
例1: 计算:
(1)
(2) sin2600+cos2600
老师提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
b
A
B
C
a
┌
c
1、根据上述规律,
2、请你用如图所示的三角形,对上题中结论的正确性进行证明。
要熟练掌握特殊锐角的三角函数值,并理解常用的关系式:
对这些关系式要学会灵活运用
设计意图
在直角三角形中,除直角外的5个元素之间有何关系?
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
sinA=
a
c
cosA=
tanA=
A
C
B
a
b
c
b
c
a
b
锐角三角函数
解直角三角形
解直角三角形的知识在解决实际问题中有广泛的应用。因此要掌握直角三角形的一般解法,即已知一边一角和已知两边的两种情况,有时要与方程、不等式、相似三角形及圆等知识结合在一起,要注意各种方法的灵活运用.同时要注意常用辅助线的画法:构造直角三角形。
解直角三角形的实际应用
解直角三角形的知识在生活和生产中有广泛的应用,如在测量高度、距离、角度,确定方案时都常用到解直角三角形。解这类题关键是把实际问题转化为数学问题,常通过作辅助线构造直角三角形来解决问题。
坡度
坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母 表示,则如图,坡度通常写成 的形式。
坡角:坡面与水平面的夹角叫做破角,用字母 表示。
h
l
弄清坡度、坡角、水平距离、垂直距离、等概念的意义,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题.
(2011湖南衡阳,9,3分)如图所示,河堤横断面迎水坡AB的坡比是1:√3 ,堤高BC=
5m,则坡面AB的长度是( )
解直角三角形的实际应用
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
如图1,某海防哨所O发现在它的北偏西30°,距离500m的A处有一艘船.该船向正东方向航行,经过3分到达哨所东北方向的B处.求这船的航速是每时多少km( 取1.7)
图1
解: 设AB与正北方向线交于点C,则OC⊥AB.
在Rt△AOC中,OA= ,∠AOC= ,
500m
30°
∴AC=OAsin∠AOC=500sin30°=500× =250(m).
OC=OAcos∠AOC=500cos30°=500× =250 (m).
在Rt△COB中, ∠BOC= 45°,
∴BC=OC=250 (m).
∴AB=AC+BC= 250+250 =250(1+ )
675÷3×60=13500 (m)
答:这船的航速是每时13.5km.
≈250(1+1.7)=675
选取关系式时要尽量利用原始数据,以防止“累积错误”。
解直角三角形的实际应用
(2011湖南常德,8分)青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.(如图7所示)一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,
测得B处的俯角为30°.已知AC=40米,
若灰太狼以5m/s的速度从城堡底部D
处出发,几秒钟后能抓到懒羊羊?
(结果精确到个位)
A
B
C
D
300
600
解直角三角形的转化思想
数学思想方法是数学的生命和灵魂。在本章的内容中,转化思想体现得特别突出。如求三角函数的值,三角函数关系中正弦和余弦的转化等,通常把问题转化到直角三角形中解决,在解直角三角形应用题时,把问题转化为解直角三角形的过程中体现了转化思想的数学价值。
解直角三角形的转化思想
(2011山东聊城,21,8分)被誉为东昌三宝之首的铁塔,始建于北宋时期,是我市现存的最古老的建筑,铁塔由塔身和塔座两部分组成(如图①).为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,
CD的长为6米,CD所在的水平线
CG⊥EF于点G(如图②),求铁
塔EF的高(结果精确到0.1米).
按照题中的精确度进行计算,并按照题目中要求的精确度确定答案以及注明单位.
1、解直角三角形的方法遵循“有斜用弦,无斜用切;
宁乘勿除,化斜为直”。
方法指导
2、选择合适的边角关系式,使计算尽可能简单,且不易出错.
让学生学会总结,对思想方法进行提炼,加深理解和记忆 。
设计意图
根据自己实际情况进一步巩固和应用所学知识。
设计意图
教学经验表明,三角函数定义“简单易记”,学生很容易轻视它,不少学生机械记忆、一知半解。本章坚持“学生主体、教师主导”的原则,采用“启发探索、讲练结合”的常规教学方法,围绕学生的学习目标设计了一系列符合学生认知规律的问题,层层深入,力求使学生体会定义产生、发展的过程及作用,培养学生自主学习能力 。
锐角三角函数
教材分析
教法学法
教学过程
反思评价
学情分析
以上是我仅从说教材、说学情、说教法、说学法、说教学程序上对本章内容的分析。希望各位领导 、同行对本堂说课提出宝贵意见。
锐角三角函数
教材分析
教法学法
教学过程
内容处理
学情分析
锐角三角函数
锐角三角函数
教材分析
地位作用
重点难点
教学目标
教材分析
教法学法
教学过程
反思评价
学情分析
知识目标:理解锐角三角函数定义和直角三 角形的解法
能力目标:培养运用图形分析问题的能力
情感目标:通过主动探究,合作交流,感受探索的乐趣和成功的体验,体会数学的合理性和严谨性。
起着承前启后的作用
重点:锐角三角函数定义和直角三角形的解法
难点:正确理解锐角三角函数的概念
锐角三角函数
学情分析
学习特点
已有基础
学习了相似三角形与勾股定理等知识的基础上
学生更侧重背公式,忽视对公式推导和概念的理解
教材分析
教法学法
教学过程
学情分析
反思评价
锐角三角函数
教法学法
学法
教法
讲授法、讨论法相结合
教师要指导学生课前预习,并且思考如下问题,本节课与以前学过的知识有什么联系,什么区别,体现出什么思想方法?
教材分析
教法学法
教学过程
学情分析
反思评价
教学过程流程图:
教学过程
教材分析
教法学法
教学过程
学情分析
反思评价
锐角三角函数
复习引入
概念形成
概念深化
堂清
应用举例
归纳小结
在图中,由于∠ACB=∠AED=90°,∠A=∠A,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角A的度数一定
时,不管三角形的大小如何,∠A的 都是一个固定值.
任意画一个角∠A,在一条边上任取两点B、D,分别过B、D向另一边作垂线BC、DE,那么 与 有什么关系.为什么? 与 呢?
探究
A
B
C
E
D
A'
B'
C'
对边与邻边的比
邻边与斜边的比
对边与斜边的比
内容处理
让学生体会定义的发生发展过程,从而理解,突破难点。
设计意图
=
a
c
sinA=
在Rt△ABC中
=
b
c
cosA=
=
a
b
tanA=
归纳
方法指导
脑中有“图”,心中有“式”
α
对边
邻边
斜边
锐角三角函数的定义在解某些问题时可用作一种基本的方法,要熟练掌握锐角三角函数。
设计意图
定义中应该注意的几个问题:
1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA、 cosA、tanA是一个比值(数值)。
3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
A
B
C
30°
x
2x
sin30°=
cos30°=
tan30°=
2
3
300角的各类三角函数值的探索
在直角三角形中,如果一个锐角等于300,那么它所对的直角边等于斜边的一半。
(4)sin450,sin600等于多少
(5)cos450,cos600等于多少
(6)tan450,tan600等于多少
┌
┌
300
600
450
450
小组间讨论
此处做法简单,思想重要。将形与数结合了起来,体现出了一种重要的思想方法——数形结合法。
设计意图
三角函数
锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
例1: 计算:
(1)
(2) sin2600+cos2600
老师提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
b
A
B
C
a
┌
c
1、根据上述规律,
2、请你用如图所示的三角形,对上题中结论的正确性进行证明。
要熟练掌握特殊锐角的三角函数值,并理解常用的关系式:
对这些关系式要学会灵活运用
设计意图
在直角三角形中,除直角外的5个元素之间有何关系?
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
sinA=
a
c
cosA=
tanA=
A
C
B
a
b
c
b
c
a
b
锐角三角函数
解直角三角形
解直角三角形的知识在解决实际问题中有广泛的应用。因此要掌握直角三角形的一般解法,即已知一边一角和已知两边的两种情况,有时要与方程、不等式、相似三角形及圆等知识结合在一起,要注意各种方法的灵活运用.同时要注意常用辅助线的画法:构造直角三角形。
解直角三角形的实际应用
解直角三角形的知识在生活和生产中有广泛的应用,如在测量高度、距离、角度,确定方案时都常用到解直角三角形。解这类题关键是把实际问题转化为数学问题,常通过作辅助线构造直角三角形来解决问题。
坡度
坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母 表示,则如图,坡度通常写成 的形式。
坡角:坡面与水平面的夹角叫做破角,用字母 表示。
h
l
弄清坡度、坡角、水平距离、垂直距离、等概念的意义,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题.
(2011湖南衡阳,9,3分)如图所示,河堤横断面迎水坡AB的坡比是1:√3 ,堤高BC=
5m,则坡面AB的长度是( )
解直角三角形的实际应用
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
如图1,某海防哨所O发现在它的北偏西30°,距离500m的A处有一艘船.该船向正东方向航行,经过3分到达哨所东北方向的B处.求这船的航速是每时多少km( 取1.7)
图1
解: 设AB与正北方向线交于点C,则OC⊥AB.
在Rt△AOC中,OA= ,∠AOC= ,
500m
30°
∴AC=OAsin∠AOC=500sin30°=500× =250(m).
OC=OAcos∠AOC=500cos30°=500× =250 (m).
在Rt△COB中, ∠BOC= 45°,
∴BC=OC=250 (m).
∴AB=AC+BC= 250+250 =250(1+ )
675÷3×60=13500 (m)
答:这船的航速是每时13.5km.
≈250(1+1.7)=675
选取关系式时要尽量利用原始数据,以防止“累积错误”。
解直角三角形的实际应用
(2011湖南常德,8分)青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.(如图7所示)一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,
测得B处的俯角为30°.已知AC=40米,
若灰太狼以5m/s的速度从城堡底部D
处出发,几秒钟后能抓到懒羊羊?
(结果精确到个位)
A
B
C
D
300
600
解直角三角形的转化思想
数学思想方法是数学的生命和灵魂。在本章的内容中,转化思想体现得特别突出。如求三角函数的值,三角函数关系中正弦和余弦的转化等,通常把问题转化到直角三角形中解决,在解直角三角形应用题时,把问题转化为解直角三角形的过程中体现了转化思想的数学价值。
解直角三角形的转化思想
(2011山东聊城,21,8分)被誉为东昌三宝之首的铁塔,始建于北宋时期,是我市现存的最古老的建筑,铁塔由塔身和塔座两部分组成(如图①).为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,
CD的长为6米,CD所在的水平线
CG⊥EF于点G(如图②),求铁
塔EF的高(结果精确到0.1米).
按照题中的精确度进行计算,并按照题目中要求的精确度确定答案以及注明单位.
1、解直角三角形的方法遵循“有斜用弦,无斜用切;
宁乘勿除,化斜为直”。
方法指导
2、选择合适的边角关系式,使计算尽可能简单,且不易出错.
让学生学会总结,对思想方法进行提炼,加深理解和记忆 。
设计意图
根据自己实际情况进一步巩固和应用所学知识。
设计意图
教学经验表明,三角函数定义“简单易记”,学生很容易轻视它,不少学生机械记忆、一知半解。本章坚持“学生主体、教师主导”的原则,采用“启发探索、讲练结合”的常规教学方法,围绕学生的学习目标设计了一系列符合学生认知规律的问题,层层深入,力求使学生体会定义产生、发展的过程及作用,培养学生自主学习能力 。
锐角三角函数
教材分析
教法学法
教学过程
反思评价
学情分析
以上是我仅从说教材、说学情、说教法、说学法、说教学程序上对本章内容的分析。希望各位领导 、同行对本堂说课提出宝贵意见。
