初中数学人教版九年级下册第二十八章 锐角三角函数复习课件(20张PPT)
文档属性
| 名称 | 初中数学人教版九年级下册第二十八章 锐角三角函数复习课件(20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-23 21:07:43 | ||
图片预览






文档简介
(共20张PPT)
锐角三角函数 复习
本章知识结构梳理
锐角三角函数
1、锐角三角函数的定义
⑴正弦;
⑵余弦;
⑶正切。
2、特殊角的三角函数值。
3、解直角三角形
⑴定义;
⑵五元素的关系
①三边间关系;
②锐角间关系;
③边角间关系。
⑶解直角三角形在实际问题中
的应用。
小结
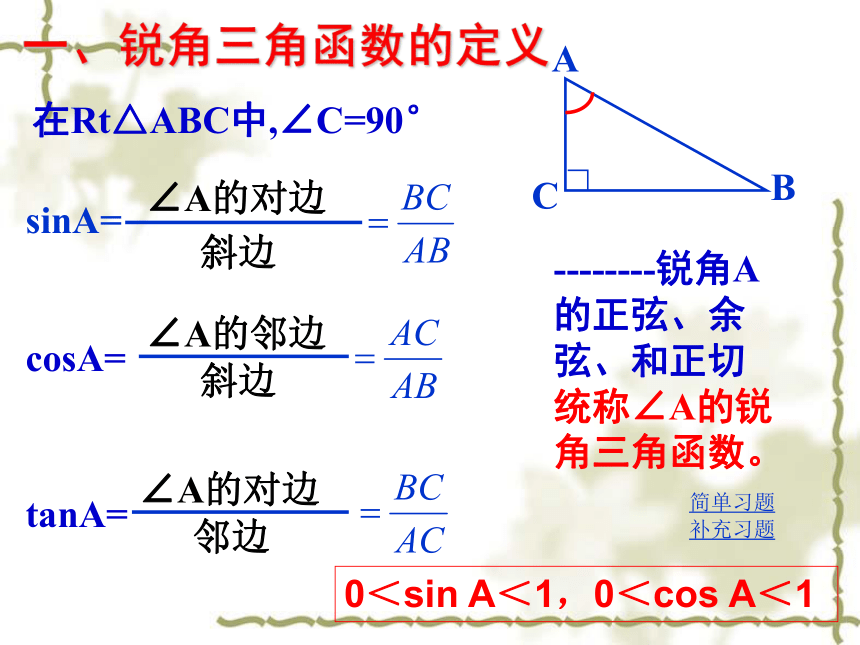
一、锐角三角函数的定义
A
B
C
∟
在Rt△ABC中,∠C=90°
cosA=
tanA=
斜边
∠A的对边
sinA=
斜边
∠A的邻边
邻边
∠A的对边
--------锐角A的正弦、余弦、和正切统称∠A的锐角三角函数。
0<sin A<1,0<cos A<1
简单习题
补充习题
【定义的应用】
2、在Rt△ABC中,∠C=90°.
若cosA= , 则tanB= .
A
B
C
∟
3x
5x
4x
3、若为锐角,则 = .
A
2
C
1
B
1、求出图中∠A的正弦值、余弦值和正切值
补充知识
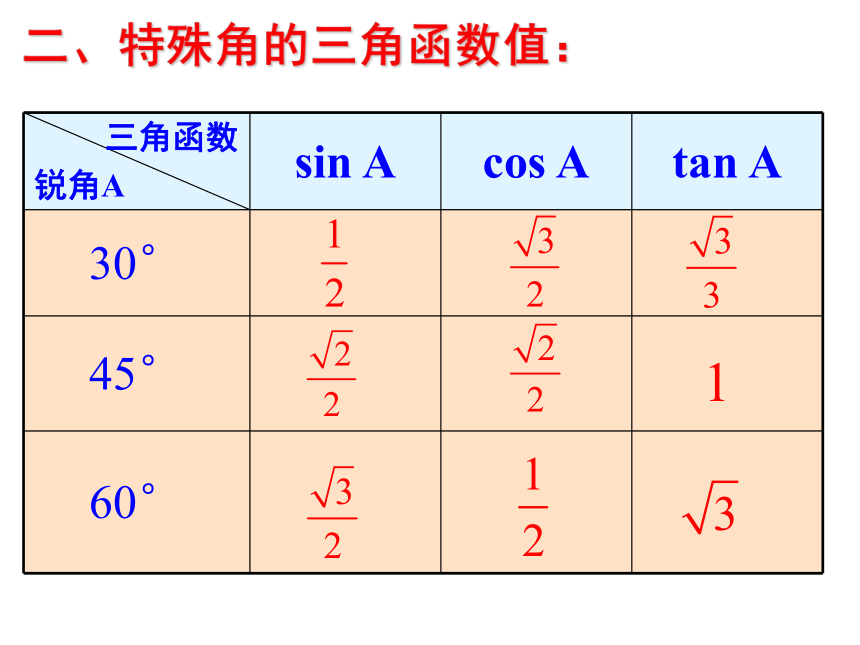
三角函数
锐角A sin A cos A tan A
30°
45°
60°
二、特殊角的三角函数值:
【特殊角三角函数值的应用】
1、计算
2、已知△ABC满足
,则△ABC是______三角形.
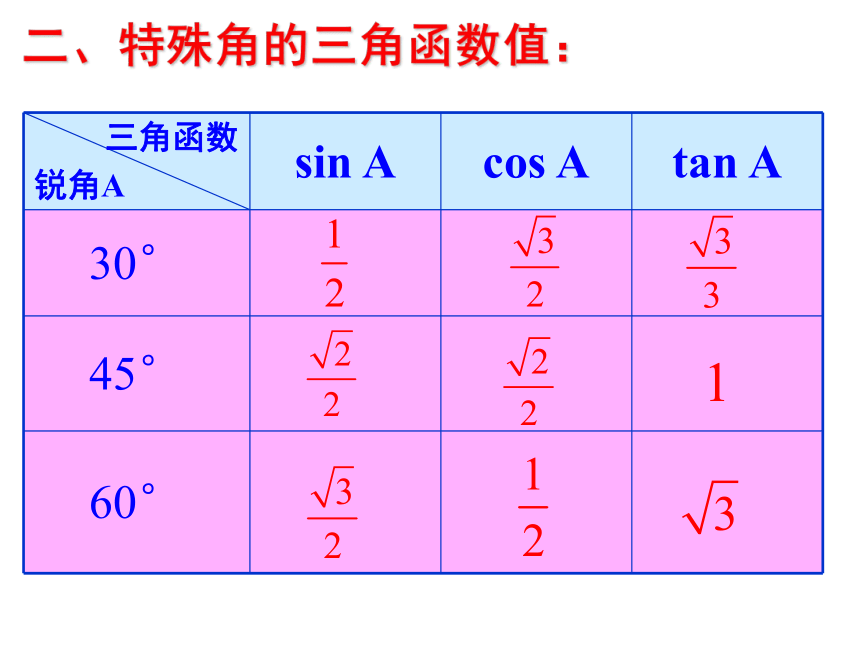
三角函数
锐角A sin A cos A tan A
30°
45°
60°
二、特殊角的三角函数值:
锐角三角函数值的变化:
当锐角A变大时,
sinA、tanA随角度的增大而 ,
cosA随角度的增大而 .
增大
减小
锐角三角函数值的变化:
当锐角A变大时,
sinA、tanA随角度的增大而 ,
cosA随角度的增大而 .
增大
减小
练习2:判断大小 sin 50° cos 50°
sin 45°=cos 45°
>
三、解直角三角形
由直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.
1.什么叫解直角三角形?
2.直角三角形中的边角关系:
∠A十∠B=90°
(1)三边关系:
(勾股定理)
(2)两锐角的关系:
(3)边角的关系:
【单个三角形中的应用】
1、在Rt△ABC中,∠C=90°,根据条件,解下
列直角三角形:
(1)a=3,∠A=30°,则b= ;c= ;
(3)∠A=30°,∠B=60°.能解直角三角形吗?
(2)a= ,c=6,则∠A= ,b= ;
注意:可解直角三角形,至少要知道一边。
没有已知边的直角三角形为不可解三角形
关键是通过图形选择合适的三角函数
A
B
C
∟
2、
在
Rt
△
ABC
中,∠
C
=
90
°,∠
B
=
35
°,
AB
=
7
,
则
BC
的长为
(
)
A
.
7sin35
°
B.
7
cos35
°
C
.
7cos35
°
D
.
7tan35
7
35°
cos35°=
∴BC=7 cos35°
C
【单个三角形中的应用】
如图,在Rt△ABC中,∠C=90°, ∠CAB=45°,∠CAD=30°,CD= ,
求AC,AB的长.
A
B
D
C
30°
【组合三角形中的应用】
已知:AC⊥BD,∠DAC=30°,
∠CAB=45°, BC= ,
求AC,AD的长.
【变式】
已知:∠C=90°,BD=2,
∠CAB=45°,∠CAD=30°,
求AC,AB的长.
A
B
D
C
30°
2
D
A
C
B
45°
30°
X
1
2
【变式】
A
已知:AC⊥BD,∠DAC=30°
∠CAB=45°, BD= ,
求AC的长.
D
30°
已知:∠C=45°,
∠B=30°,BC= ,
求AC,AB的长.
C
A
B
45°
C
B
45°
D
30°
X
X
X
小结
(1)将实际问题化为数学问题;
(画出图形、转化为直角三角形问题)
(2)选择适当的三角函数解直角三角形;
(3)将数学答案写为实际问题答案。
解直角三角形的实际应用
小结
某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望灯塔C恰在西北方向,若船速为每小时20海里,求A、D两点间的距离。
E
30°
x
10
【实际问题中的应用】
小结
几种基本图形
解直角三角形的实际应用
小结
通过这节课,你学到了什么?
4.在△ABC中,若BC= ,AB= , AC=3,
【课堂练习】
一、基础训练
∠B=30°, 则∠BAC的度数是______.
则cosA=________.
1.(2023年沈阳市)在△ABC中,AB=2,AC=
2.计算2sin30°-2cos60°+tan45°=________.
3.(2023年辽宁省)在Rt△ABC中,∠C=90°, AB=5,
AC=3,则sinB=_____.
锐角三角函数 复习
本章知识结构梳理
锐角三角函数
1、锐角三角函数的定义
⑴正弦;
⑵余弦;
⑶正切。
2、特殊角的三角函数值。
3、解直角三角形
⑴定义;
⑵五元素的关系
①三边间关系;
②锐角间关系;
③边角间关系。
⑶解直角三角形在实际问题中
的应用。
小结
一、锐角三角函数的定义
A
B
C
∟
在Rt△ABC中,∠C=90°
cosA=
tanA=
斜边
∠A的对边
sinA=
斜边
∠A的邻边
邻边
∠A的对边
--------锐角A的正弦、余弦、和正切统称∠A的锐角三角函数。
0<sin A<1,0<cos A<1
简单习题
补充习题
【定义的应用】
2、在Rt△ABC中,∠C=90°.
若cosA= , 则tanB= .
A
B
C
∟
3x
5x
4x
3、若为锐角,则 = .
A
2
C
1
B
1、求出图中∠A的正弦值、余弦值和正切值
补充知识
三角函数
锐角A sin A cos A tan A
30°
45°
60°
二、特殊角的三角函数值:
【特殊角三角函数值的应用】
1、计算
2、已知△ABC满足
,则△ABC是______三角形.
三角函数
锐角A sin A cos A tan A
30°
45°
60°
二、特殊角的三角函数值:
锐角三角函数值的变化:
当锐角A变大时,
sinA、tanA随角度的增大而 ,
cosA随角度的增大而 .
增大
减小
锐角三角函数值的变化:
当锐角A变大时,
sinA、tanA随角度的增大而 ,
cosA随角度的增大而 .
增大
减小
练习2:判断大小 sin 50° cos 50°
sin 45°=cos 45°
>
三、解直角三角形
由直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.
1.什么叫解直角三角形?
2.直角三角形中的边角关系:
∠A十∠B=90°
(1)三边关系:
(勾股定理)
(2)两锐角的关系:
(3)边角的关系:
【单个三角形中的应用】
1、在Rt△ABC中,∠C=90°,根据条件,解下
列直角三角形:
(1)a=3,∠A=30°,则b= ;c= ;
(3)∠A=30°,∠B=60°.能解直角三角形吗?
(2)a= ,c=6,则∠A= ,b= ;
注意:可解直角三角形,至少要知道一边。
没有已知边的直角三角形为不可解三角形
关键是通过图形选择合适的三角函数
A
B
C
∟
2、
在
Rt
△
ABC
中,∠
C
=
90
°,∠
B
=
35
°,
AB
=
7
,
则
BC
的长为
(
)
A
.
7sin35
°
B.
7
cos35
°
C
.
7cos35
°
D
.
7tan35
7
35°
cos35°=
∴BC=7 cos35°
C
【单个三角形中的应用】
如图,在Rt△ABC中,∠C=90°, ∠CAB=45°,∠CAD=30°,CD= ,
求AC,AB的长.
A
B
D
C
30°
【组合三角形中的应用】
已知:AC⊥BD,∠DAC=30°,
∠CAB=45°, BC= ,
求AC,AD的长.
【变式】
已知:∠C=90°,BD=2,
∠CAB=45°,∠CAD=30°,
求AC,AB的长.
A
B
D
C
30°
2
D
A
C
B
45°
30°
X
1
2
【变式】
A
已知:AC⊥BD,∠DAC=30°
∠CAB=45°, BD= ,
求AC的长.
D
30°
已知:∠C=45°,
∠B=30°,BC= ,
求AC,AB的长.
C
A
B
45°
C
B
45°
D
30°
X
X
X
小结
(1)将实际问题化为数学问题;
(画出图形、转化为直角三角形问题)
(2)选择适当的三角函数解直角三角形;
(3)将数学答案写为实际问题答案。
解直角三角形的实际应用
小结
某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望灯塔C恰在西北方向,若船速为每小时20海里,求A、D两点间的距离。
E
30°
x
10
【实际问题中的应用】
小结
几种基本图形
解直角三角形的实际应用
小结
通过这节课,你学到了什么?
4.在△ABC中,若BC= ,AB= , AC=3,
【课堂练习】
一、基础训练
∠B=30°, 则∠BAC的度数是______.
则cosA=________.
1.(2023年沈阳市)在△ABC中,AB=2,AC=
2.计算2sin30°-2cos60°+tan45°=________.
3.(2023年辽宁省)在Rt△ABC中,∠C=90°, AB=5,
AC=3,则sinB=_____.
