沪教版八年级数学上册试题 第十九章《 几何证明》单元复习题 (含解析)
文档属性
| 名称 | 沪教版八年级数学上册试题 第十九章《 几何证明》单元复习题 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-24 09:10:48 | ||
图片预览



文档简介
第十九章《 几何证明》单元复习题
一、单选题
1.下列命题的逆命题是假命题的是
A.等腰三角形的两个底角相等 B.两直线平行,内错角相等
C.全等三角形三条对应边相等 D.全等三角形的周长相等
2.在下列四组数中,属于勾股数的是( )
A.0.3,0.4,0.5 B.7,24,25 C.,, D.1,,
3.如图,在中,,,,,则的长为( )
A.1.5 B.2 C.3 D.4
4.在直角坐标系中,已知点、,则线段的长度是( ).
A.1 B. C. D.2
5.如图,在中,,是的中线,,,则的长等于( )
A. B. C. D.
6.如图,点D在的边BC上,点P在射线上(不与点A,D重合),连接,.下列命题中,假命题是( )
A.若,,则
B.若,,则
C.若,,则
D.若,,则
7.如图,在中,,的平分线交于点,于点,若的周长为,则的周长为,则( )
A. B. C. D.
8.一艘渔船从港口沿北偏东60°方向航行60海里到达处时突然发生故障,位于港口正东方向的处的救援艇接到信号后,立即沿北偏东45°方向以40海里/小时的速度前去救援,救援艇到达处所用的时间为( )
A.小时 B.小时 C.小时 D.小时
9.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为8cm,则正方形a、b、c、d、e、f、g面积的和是( )cm2.
A.64 B.81 C.128 D.192
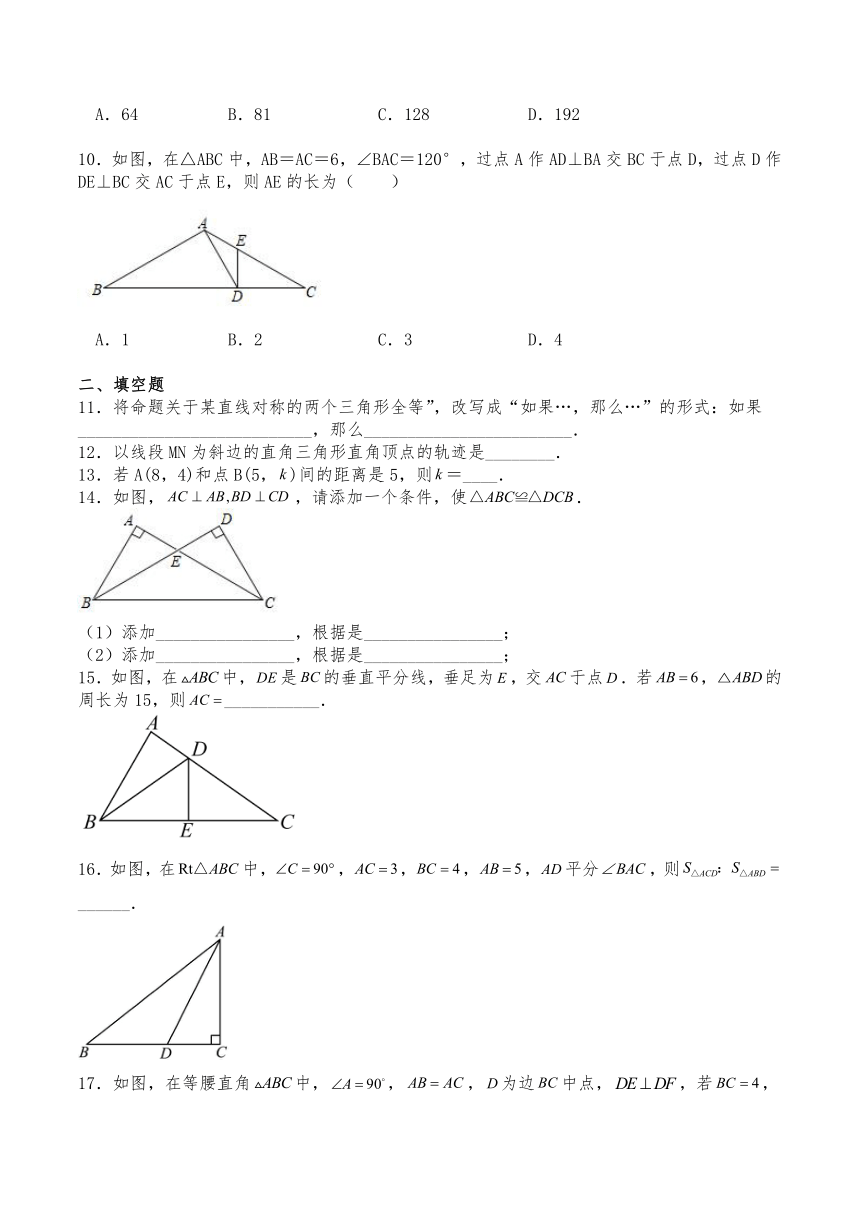
10.如图,在△ABC中,AB=AC=6,∠BAC=120°,过点A作AD⊥BA交BC于点D,过点D作DE⊥BC交AC于点E,则AE的长为( )
A.1 B.2 C.3 D.4
二、填空题
11.将命题关于某直线对称的两个三角形全等”,改写成“如果…,那么…”的形式:如果___________________________,那么________________________.
12.以线段MN为斜边的直角三角形直角顶点的轨迹是________.
13.若A(8,4)和点B(5,)间的距离是5,则=____.
14.如图,,请添加一个条件,使.
(1)添加________________,根据是________________;
(2)添加________________,根据是________________;
15.如图,在中,是的垂直平分线,垂足为,交于点.若,的周长为15,则___________.
16.如图,在中,,,,,平分,则 ______.
17.如图,在等腰直角中,,,为边中点,,若,则四边形AEDF的面积为___________.
18.如图,点是的边的中点,将沿直线翻折能与重合,若,,,则点到直线的距离为________
三、解答题
19.已知命题“等腰三角形底边上的高线与顶角的平分线重合”.
(1)请写出它的逆命题;
(2)判断该逆命题的真假,若为假命题,请说明理由,若为真命题,请证明.
20.在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAB=∠B+30°,CE=2cm.
求∶(1)∠AEB 度数.
(2)BC的长.
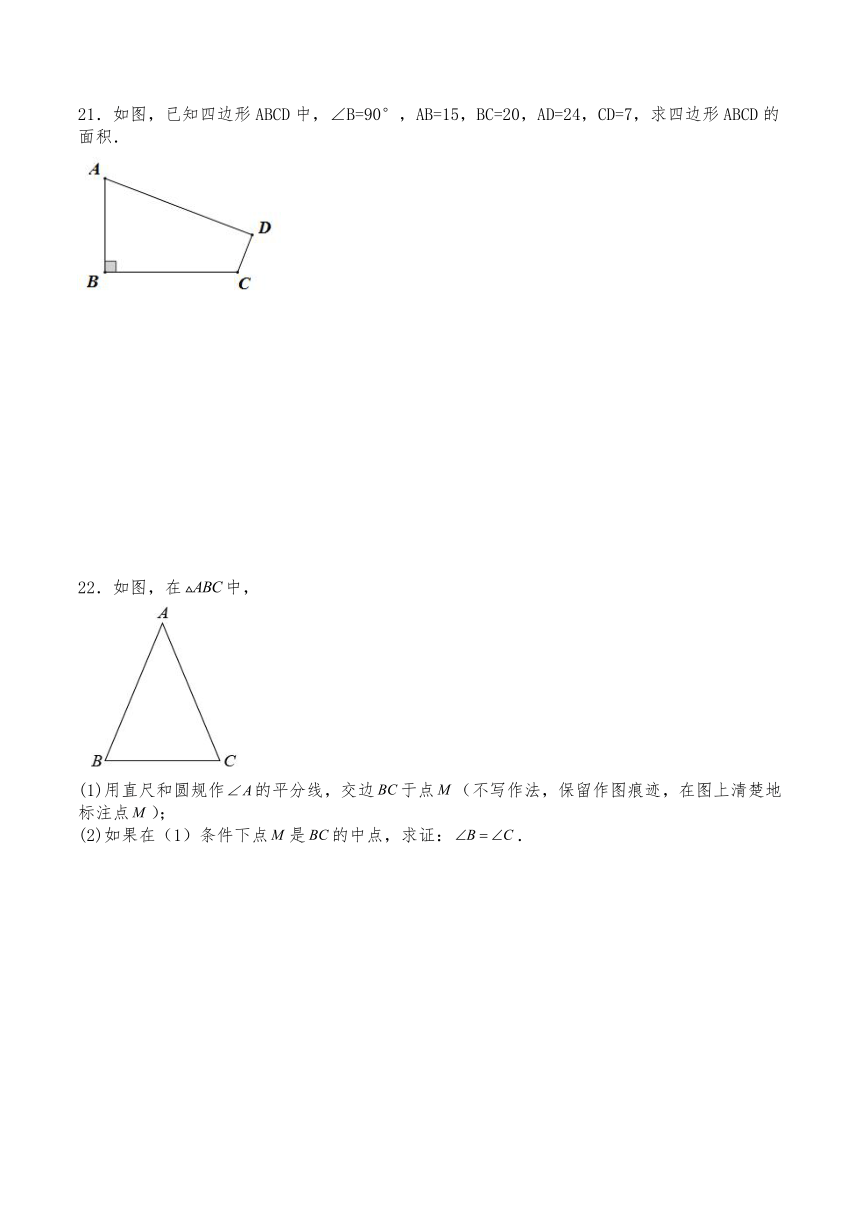
21.如图,已知四边形ABCD中,∠B=90°,AB=15,BC=20,AD=24,CD=7,求四边形ABCD的面积.
22.如图,在中,
(1)用直尺和圆规作的平分线,交边于点(不写作法,保留作图痕迹,在图上清楚地标注点);
(2)如果在(1)条件下点是的中点,求证:.
23.如图:已知 BAC=30°,AT平分BAC,TE∥AC.
(1)求证:是等腰三角形;
(2)若,垂足为点D,AE=4cm,求TD的长.
24.已知:如图,在Rt△ABC中,∠ACB=90°,将这个三角形绕点A旋转,使点B落在边BC延长线上的点D处,点C落在点E处.求证:AD垂直平分线段CE.
25.如图,在中,,把绕点B逆时针旋转,得到,点E在上,若,求及的长.
26.如图,在△ABC中,∠ACB=90°,AC=BC,E为AB中点,ED∥BC,且与∠ABC的平分线BD交于点D,联结AD.
(1)求证:AD⊥BD;
(2)记BD与AC的交点为F,求证:BF=2AD.
27.如图,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为点E,F,DB=DC.
(1)求证:BE=CF;
(2)如果BD//AC,∠DAF=15°,求证:AB=2DF.
28.在平面直角坐标系中有一等腰三角形,点A在y轴正半轴上,点B在x轴负半轴上.
(1)如图1,点C在第一象限,若,A、B两点的坐标分别是,,求C点的坐标;
(2)如图2,点C在x正半轴上,点E、F分别是边、上的点,若.求证:;
(3)如图3,点C与点O重合时点E在第三象限,,连接,求的度数.
29.如图,是等腰直角三角形,, ,D在线段上,E是线段上一点.现以为直角边,C为直角顶点,在的下方作等腰直角,连接.
(1)如图1,求证:;
(2)当A、E、F三点共线时,如图2,若,求的长;
(3)如图3,若,连接,当E运动到使得时,求的面积.
答案
一、单选题
1.D
【分析】根据真命题和假命题的定义以及逆命题与逆定理的定义分别判断得出即可.
【解析】A、等腰三角形的两个底角相等的逆命题是:两个角相等的三角形是等腰三角形,说法正确,是真命题;
B、两直线平行,内错角相等的逆命题为“内错角相等,两直线平行”,逆命题为真命题,说法正确,是真命题;
C、全等三角形三条对应边相等的逆命题是:三条对应边相等的是全等三角形,说法正确,是真命题;
D、全等三角形的周长相等的逆命题是:周长相等的三角形是全等三角形,说法错误,是假命题;
故选D.
2.B
【分析】利用勾股数的定义进行分析.
【解析】、,0.4,0.5都不是正整数,,0.4,0.5不是勾股数,不符合题意;
、,,24,25是勾股数,符合题意;
、,,都不是正整数,,,不是勾股数,不符合题意;
、,,都不是正整数,,,不是勾股数,不符合题意.
故选:.
3.B
【分析】根据直角三角形两锐角互余求出,然后根据角所对的直角边等于斜边的一半求出,再求出,然后求出,从而得到,根据等角对等边可得,从而得解.
【解析】解:,,
,
,
,,
,
,
,
.
故选:B.
4.B
【分析】本题考查的是两点之间的距离公式,根据直角坐标系中两点间的距离等于横坐标差的平方加上纵坐标差的平方,再开算术平方根解答即可
【解析】解:将A、B两点坐标代入带距离公式中有,所以答案选B
5.D
【分析】根据直角三角形斜边的中线等于斜边的一半,计算即可得出结果.
【解析】解:∵,
∴是直角三角形,
∵是的中线,
∴,
∵,
∴.
故选:D
6.D
【分析】根据等腰三角形性质以及垂直平分线的性质逐项判断即可.
【解析】解:若,,则D是中点,
∴是的垂直平分线,
∴,
∴故选项A是真命题,不符合题意;
,即,
又,
∴是的垂直平分线,
∴,
∴故选项B是真命题,不符合题意;
若,,则,D是中点,
∴是的垂直平分线,
∴,
∴故选项C是真命题,不符合题意;
若,,不能得到,故选项D是假命题,符合题意;
故选:D.
7.A
【分析】根据角平分线的性质得出,再根据全等三角形的判定与性质、三角形的周长公式即可求解.
【解析】解:在中,,的平分线交于点,于点,
,
的周长为,
,
,
的周长为,
,
在和中,
∵,
≌,
.
故选:A.
8.D
【分析】过点C作,垂足为点D,先求出的长度,再根据勾股定理求出的长度即可.
【解析】解:过点C作,垂足为点D,
∵,海里,
∴海里,
∵,
∴,
根据勾股定理得:海里,
∴救援艇到达处所用的时间为:.
故选:D.
9.D
【分析】根据勾股定理可知,Sg = Se+Sf=Sa+Sb+Sc+Sd,求出最大正方形的面积即可求解.
【解析】解:根据勾股定理知,
Sg= Se+Sf,Se=Sa+Sb, Sf= Sc+Sd,
∴Sg = Se+Sf=Sa+Sb+Sc+Sd,
∵最大的正方形的面积为Sg =(8×8)cm2=64cm2,
∴正方形a、b、c、d、e、f、g面积的和是64×3=192cm2,
故选D.
10.B
【分析】根据等腰三角形的性质可得,根据含角的直角三角形的性质可得的长,再求出的长,即可确定的长.
【解析】解:,,
,
,
,
设,则,
根据勾股定理,可得,
解得或(舍去),
,
,
,
,
,
,
设,则,
根据勾股定理,得,
或(舍去),
,
,
故选:B.
二、填空题
11. 两个三角形关于某直线对称; 这两个三角形全等.
【分析】任何一个命题都可以写成“如果…那么…”的形式,如果是条件,那么是结论.
【解析】解:关于某直线对称的两个三角形全等,改写成“如果…,那么…”的形式:
如果两个三角形关于某直线对称,那么这两个三角形全等
故答案为:两个三角形关于某直线对称;这两个三角形全等
12.以MN为直径圆(除M、N两点外)
【分析】根据直角三角形的性质,斜边即为外接圆的直径,故可确定答案.
【解析】根据直角三角形的性质,斜边即为外接圆的直径,
故以线段MN为斜边的直角三角形直角顶点的轨迹是以线段MN中点为圆心,MN为直径的圆(不包含M、N两点).
故答案为:以MN为直径圆(除M、N两点外).
13.8或0
【分析】根据两点的距离公式解答即可.
【解析】根据两点的距离公式得(8-5)2+(k-4)2=52,解得k=8或0,
故答案为:8或0.
14.
【分析】(1)添加条件,再由条件:,可根据定理证明;
(2)添加,同理由条件可以推导.
【解析】解:(1)添加.
理由:,
,
,,
(2)添加.
理由:,
,
,,
故答案为:,;,(答案不唯一).
15.9
【分析】根据线段的垂直平分线的性质得到,根据三角形的周长公式即可得到答案.
【解析】解:∵是的垂直平分线,
∴,
∴的周长,
∵,
∴
故答案为:9.
16.
【分析】过点作于,根据角平分线的性质得到,根据三角形的面积公式计算,得到答案.
【解析】解:过点作于,
∵平分,,,
∴,
∴:,
故答案为:.
17.
【分析】先连接,根据等腰直角三角形的性质,求得,,,进而判定,得出即可.
【解析】解:连接,如下图
由题意可得:,,
∴
∴
∴
∴
故答案为:
18.
【分析】连接,延长交于点,作于点,如图所示,由折叠的性质及中点性质可得三角形为直角三角形,且为中点,从而,由勾股定理可得的长,再根据,即,从而可求得的长.
【解析】连接,延长交于点,作于点,如图所示,
由折叠的性质可得:,,
则为的中垂线,
,
为中点,
,,,
,,
,
即,
,
即,
在直角三角形中,由勾股定理可得:
,
,
,
,
,
.
故答案为:.
三、解答题
19.(1)原命题的条件是:三角形是等腰三角形;结论是:底边上的高线和顶角的角平分线重合,
∴逆命题是:底边上的高线和顶角的角平分线重合的三角形是等腰三角形.
(2)该逆命题是真命题,证明如下:
如图,已知:△ABC中,AD是BC边的高线也是顶角∠BAC的角平分线.
求证:AB=AC.
∵AD是BC边的高,
∴AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AD是∠BAC的角平分线,
∴∠BAD=∠CAD,
在△BAD和△CAD中,,
∴AB=AC.
20.(1)解:∵DE垂直平分斜边AB
∴EA=EB
∴∠EAB=∠B
∵∠CAB=∠B+30°且∠CAB=∠CAE+∠EAB
∴∠CAE=30°
∴∠AEB=∠CAE+∠C=30°+90°=120°
(2)在△ACE中,
∵∠C=90°,∠CAE=30°,
∴AE=2CE=4,
又∵AE=BE,
∴BC=CE+BE=6cm.
21.解:连接AC,如图,
∵,
∴,
∵AD2+CD2=242+72=625,AC2=252=625,
∴AD2+CD2=AC2,
∴∠D=90°,
∴S四边形ABCD=S△ABC+S△ACD=.
22.(1)解:作图如下:
(2)证明:如图,作交于点;作交于点;
由(1)可知:平分
∴
∵点是的中点
∴
在和中
∴
∴
23.解:(1)∵AT平分BAC.
∴∠EAT=∠TAD.
∵TE∥AC.
∴∠TAD=∠ETA.
∴∠EAT=∠ETA.
∴是等腰三角形.
(2)过点T作TFAB,垂足点F,
∵AT平分BAC,TFAB,.
∴据角平分线定理可得DT=TF.
∵在RT△TFE中,ET=4cm,∠FET=30°,则TF=2cm,
∴TD=2cm.
24.∵△ADE是由△ABC旋转得到,
∴AD=AB,AE=AC,∠DAE=∠BAC,
∵AD=AB,
∴∠ADC=∠B,
∵∠ACB=90°,
∴∠DAC=∠BAC,
∴∠DAC=∠DAE,
∵AE=AC,
∴AD垂直平分线段CE.
25.解:由旋转的性质可得,
在中,由勾股定理得:,
∴,
在中,由勾股定理得:.
26.
(1)
解:证明:为中点,
,
BD平分∠ABC,
,
,
,
,
,
,
,
,
,
,
;
(2)
解:延长,交于点,
在和中,
,
,
,
,
,
,
,
在和中,
,
,
,
.
27.证明:(1)平分,, ,
,;
在和中,
,
,
;
(2)平分,,
,,
,
,,
,
,
在中,,
,
,
平分,, ,
,
.
28.(1)解:如图1中,过点C作,垂足为M,则,
∵,
∴,,
∴,
∵是等腰三角形,,
∴,
在和中,,
∴,
∴,,
∵,,
∴,,
∴,,
∴,
∴;
(2)证明:设,则,
∵,,
∴,
由图2可知,等腰三角形中,,
∴,
∵,
∴,
∵,
,
∴,
∴,
∴,
∴;
(3)解:∵点C与点O重合,,
∴,
如图3,过点O作于点G,交的延长线于点H,与交于点M,
∵,
∴,
∵,,
∴,
又∵,,
∴,
∴,
又∵,,
∴平分,
∴,
∴.
29.(1)证明:∵都是等腰直角三角形,
∴,
∴,
∴,
∴;
(2)解:∵,
∴,
由(1)得:,
∵,
∴,
∴;
(3)解:过点F作于H,如图3所示:
∵是等腰直角三角形,,
∴,
∵,
∴,
∴,
∴,
同(1)得:,
∴,
∴,
∴,
∵,
∴,,,
∵,
∴是等边三角形,
∴,
∴
.
一、单选题
1.下列命题的逆命题是假命题的是
A.等腰三角形的两个底角相等 B.两直线平行,内错角相等
C.全等三角形三条对应边相等 D.全等三角形的周长相等
2.在下列四组数中,属于勾股数的是( )
A.0.3,0.4,0.5 B.7,24,25 C.,, D.1,,
3.如图,在中,,,,,则的长为( )
A.1.5 B.2 C.3 D.4
4.在直角坐标系中,已知点、,则线段的长度是( ).
A.1 B. C. D.2
5.如图,在中,,是的中线,,,则的长等于( )
A. B. C. D.
6.如图,点D在的边BC上,点P在射线上(不与点A,D重合),连接,.下列命题中,假命题是( )
A.若,,则
B.若,,则
C.若,,则
D.若,,则
7.如图,在中,,的平分线交于点,于点,若的周长为,则的周长为,则( )
A. B. C. D.
8.一艘渔船从港口沿北偏东60°方向航行60海里到达处时突然发生故障,位于港口正东方向的处的救援艇接到信号后,立即沿北偏东45°方向以40海里/小时的速度前去救援,救援艇到达处所用的时间为( )
A.小时 B.小时 C.小时 D.小时
9.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为8cm,则正方形a、b、c、d、e、f、g面积的和是( )cm2.
A.64 B.81 C.128 D.192
10.如图,在△ABC中,AB=AC=6,∠BAC=120°,过点A作AD⊥BA交BC于点D,过点D作DE⊥BC交AC于点E,则AE的长为( )
A.1 B.2 C.3 D.4
二、填空题
11.将命题关于某直线对称的两个三角形全等”,改写成“如果…,那么…”的形式:如果___________________________,那么________________________.
12.以线段MN为斜边的直角三角形直角顶点的轨迹是________.
13.若A(8,4)和点B(5,)间的距离是5,则=____.
14.如图,,请添加一个条件,使.
(1)添加________________,根据是________________;
(2)添加________________,根据是________________;
15.如图,在中,是的垂直平分线,垂足为,交于点.若,的周长为15,则___________.
16.如图,在中,,,,,平分,则 ______.
17.如图,在等腰直角中,,,为边中点,,若,则四边形AEDF的面积为___________.
18.如图,点是的边的中点,将沿直线翻折能与重合,若,,,则点到直线的距离为________
三、解答题
19.已知命题“等腰三角形底边上的高线与顶角的平分线重合”.
(1)请写出它的逆命题;
(2)判断该逆命题的真假,若为假命题,请说明理由,若为真命题,请证明.
20.在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAB=∠B+30°,CE=2cm.
求∶(1)∠AEB 度数.
(2)BC的长.
21.如图,已知四边形ABCD中,∠B=90°,AB=15,BC=20,AD=24,CD=7,求四边形ABCD的面积.
22.如图,在中,
(1)用直尺和圆规作的平分线,交边于点(不写作法,保留作图痕迹,在图上清楚地标注点);
(2)如果在(1)条件下点是的中点,求证:.
23.如图:已知 BAC=30°,AT平分BAC,TE∥AC.
(1)求证:是等腰三角形;
(2)若,垂足为点D,AE=4cm,求TD的长.
24.已知:如图,在Rt△ABC中,∠ACB=90°,将这个三角形绕点A旋转,使点B落在边BC延长线上的点D处,点C落在点E处.求证:AD垂直平分线段CE.
25.如图,在中,,把绕点B逆时针旋转,得到,点E在上,若,求及的长.
26.如图,在△ABC中,∠ACB=90°,AC=BC,E为AB中点,ED∥BC,且与∠ABC的平分线BD交于点D,联结AD.
(1)求证:AD⊥BD;
(2)记BD与AC的交点为F,求证:BF=2AD.
27.如图,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为点E,F,DB=DC.
(1)求证:BE=CF;
(2)如果BD//AC,∠DAF=15°,求证:AB=2DF.
28.在平面直角坐标系中有一等腰三角形,点A在y轴正半轴上,点B在x轴负半轴上.
(1)如图1,点C在第一象限,若,A、B两点的坐标分别是,,求C点的坐标;
(2)如图2,点C在x正半轴上,点E、F分别是边、上的点,若.求证:;
(3)如图3,点C与点O重合时点E在第三象限,,连接,求的度数.
29.如图,是等腰直角三角形,, ,D在线段上,E是线段上一点.现以为直角边,C为直角顶点,在的下方作等腰直角,连接.
(1)如图1,求证:;
(2)当A、E、F三点共线时,如图2,若,求的长;
(3)如图3,若,连接,当E运动到使得时,求的面积.
答案
一、单选题
1.D
【分析】根据真命题和假命题的定义以及逆命题与逆定理的定义分别判断得出即可.
【解析】A、等腰三角形的两个底角相等的逆命题是:两个角相等的三角形是等腰三角形,说法正确,是真命题;
B、两直线平行,内错角相等的逆命题为“内错角相等,两直线平行”,逆命题为真命题,说法正确,是真命题;
C、全等三角形三条对应边相等的逆命题是:三条对应边相等的是全等三角形,说法正确,是真命题;
D、全等三角形的周长相等的逆命题是:周长相等的三角形是全等三角形,说法错误,是假命题;
故选D.
2.B
【分析】利用勾股数的定义进行分析.
【解析】、,0.4,0.5都不是正整数,,0.4,0.5不是勾股数,不符合题意;
、,,24,25是勾股数,符合题意;
、,,都不是正整数,,,不是勾股数,不符合题意;
、,,都不是正整数,,,不是勾股数,不符合题意.
故选:.
3.B
【分析】根据直角三角形两锐角互余求出,然后根据角所对的直角边等于斜边的一半求出,再求出,然后求出,从而得到,根据等角对等边可得,从而得解.
【解析】解:,,
,
,
,,
,
,
,
.
故选:B.
4.B
【分析】本题考查的是两点之间的距离公式,根据直角坐标系中两点间的距离等于横坐标差的平方加上纵坐标差的平方,再开算术平方根解答即可
【解析】解:将A、B两点坐标代入带距离公式中有,所以答案选B
5.D
【分析】根据直角三角形斜边的中线等于斜边的一半,计算即可得出结果.
【解析】解:∵,
∴是直角三角形,
∵是的中线,
∴,
∵,
∴.
故选:D
6.D
【分析】根据等腰三角形性质以及垂直平分线的性质逐项判断即可.
【解析】解:若,,则D是中点,
∴是的垂直平分线,
∴,
∴故选项A是真命题,不符合题意;
,即,
又,
∴是的垂直平分线,
∴,
∴故选项B是真命题,不符合题意;
若,,则,D是中点,
∴是的垂直平分线,
∴,
∴故选项C是真命题,不符合题意;
若,,不能得到,故选项D是假命题,符合题意;
故选:D.
7.A
【分析】根据角平分线的性质得出,再根据全等三角形的判定与性质、三角形的周长公式即可求解.
【解析】解:在中,,的平分线交于点,于点,
,
的周长为,
,
,
的周长为,
,
在和中,
∵,
≌,
.
故选:A.
8.D
【分析】过点C作,垂足为点D,先求出的长度,再根据勾股定理求出的长度即可.
【解析】解:过点C作,垂足为点D,
∵,海里,
∴海里,
∵,
∴,
根据勾股定理得:海里,
∴救援艇到达处所用的时间为:.
故选:D.
9.D
【分析】根据勾股定理可知,Sg = Se+Sf=Sa+Sb+Sc+Sd,求出最大正方形的面积即可求解.
【解析】解:根据勾股定理知,
Sg= Se+Sf,Se=Sa+Sb, Sf= Sc+Sd,
∴Sg = Se+Sf=Sa+Sb+Sc+Sd,
∵最大的正方形的面积为Sg =(8×8)cm2=64cm2,
∴正方形a、b、c、d、e、f、g面积的和是64×3=192cm2,
故选D.
10.B
【分析】根据等腰三角形的性质可得,根据含角的直角三角形的性质可得的长,再求出的长,即可确定的长.
【解析】解:,,
,
,
,
设,则,
根据勾股定理,可得,
解得或(舍去),
,
,
,
,
,
,
设,则,
根据勾股定理,得,
或(舍去),
,
,
故选:B.
二、填空题
11. 两个三角形关于某直线对称; 这两个三角形全等.
【分析】任何一个命题都可以写成“如果…那么…”的形式,如果是条件,那么是结论.
【解析】解:关于某直线对称的两个三角形全等,改写成“如果…,那么…”的形式:
如果两个三角形关于某直线对称,那么这两个三角形全等
故答案为:两个三角形关于某直线对称;这两个三角形全等
12.以MN为直径圆(除M、N两点外)
【分析】根据直角三角形的性质,斜边即为外接圆的直径,故可确定答案.
【解析】根据直角三角形的性质,斜边即为外接圆的直径,
故以线段MN为斜边的直角三角形直角顶点的轨迹是以线段MN中点为圆心,MN为直径的圆(不包含M、N两点).
故答案为:以MN为直径圆(除M、N两点外).
13.8或0
【分析】根据两点的距离公式解答即可.
【解析】根据两点的距离公式得(8-5)2+(k-4)2=52,解得k=8或0,
故答案为:8或0.
14.
【分析】(1)添加条件,再由条件:,可根据定理证明;
(2)添加,同理由条件可以推导.
【解析】解:(1)添加.
理由:,
,
,,
(2)添加.
理由:,
,
,,
故答案为:,;,(答案不唯一).
15.9
【分析】根据线段的垂直平分线的性质得到,根据三角形的周长公式即可得到答案.
【解析】解:∵是的垂直平分线,
∴,
∴的周长,
∵,
∴
故答案为:9.
16.
【分析】过点作于,根据角平分线的性质得到,根据三角形的面积公式计算,得到答案.
【解析】解:过点作于,
∵平分,,,
∴,
∴:,
故答案为:.
17.
【分析】先连接,根据等腰直角三角形的性质,求得,,,进而判定,得出即可.
【解析】解:连接,如下图
由题意可得:,,
∴
∴
∴
∴
故答案为:
18.
【分析】连接,延长交于点,作于点,如图所示,由折叠的性质及中点性质可得三角形为直角三角形,且为中点,从而,由勾股定理可得的长,再根据,即,从而可求得的长.
【解析】连接,延长交于点,作于点,如图所示,
由折叠的性质可得:,,
则为的中垂线,
,
为中点,
,,,
,,
,
即,
,
即,
在直角三角形中,由勾股定理可得:
,
,
,
,
,
.
故答案为:.
三、解答题
19.(1)原命题的条件是:三角形是等腰三角形;结论是:底边上的高线和顶角的角平分线重合,
∴逆命题是:底边上的高线和顶角的角平分线重合的三角形是等腰三角形.
(2)该逆命题是真命题,证明如下:
如图,已知:△ABC中,AD是BC边的高线也是顶角∠BAC的角平分线.
求证:AB=AC.
∵AD是BC边的高,
∴AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AD是∠BAC的角平分线,
∴∠BAD=∠CAD,
在△BAD和△CAD中,,
∴AB=AC.
20.(1)解:∵DE垂直平分斜边AB
∴EA=EB
∴∠EAB=∠B
∵∠CAB=∠B+30°且∠CAB=∠CAE+∠EAB
∴∠CAE=30°
∴∠AEB=∠CAE+∠C=30°+90°=120°
(2)在△ACE中,
∵∠C=90°,∠CAE=30°,
∴AE=2CE=4,
又∵AE=BE,
∴BC=CE+BE=6cm.
21.解:连接AC,如图,
∵,
∴,
∵AD2+CD2=242+72=625,AC2=252=625,
∴AD2+CD2=AC2,
∴∠D=90°,
∴S四边形ABCD=S△ABC+S△ACD=.
22.(1)解:作图如下:
(2)证明:如图,作交于点;作交于点;
由(1)可知:平分
∴
∵点是的中点
∴
在和中
∴
∴
23.解:(1)∵AT平分BAC.
∴∠EAT=∠TAD.
∵TE∥AC.
∴∠TAD=∠ETA.
∴∠EAT=∠ETA.
∴是等腰三角形.
(2)过点T作TFAB,垂足点F,
∵AT平分BAC,TFAB,.
∴据角平分线定理可得DT=TF.
∵在RT△TFE中,ET=4cm,∠FET=30°,则TF=2cm,
∴TD=2cm.
24.∵△ADE是由△ABC旋转得到,
∴AD=AB,AE=AC,∠DAE=∠BAC,
∵AD=AB,
∴∠ADC=∠B,
∵∠ACB=90°,
∴∠DAC=∠BAC,
∴∠DAC=∠DAE,
∵AE=AC,
∴AD垂直平分线段CE.
25.解:由旋转的性质可得,
在中,由勾股定理得:,
∴,
在中,由勾股定理得:.
26.
(1)
解:证明:为中点,
,
BD平分∠ABC,
,
,
,
,
,
,
,
,
,
,
;
(2)
解:延长,交于点,
在和中,
,
,
,
,
,
,
,
在和中,
,
,
,
.
27.证明:(1)平分,, ,
,;
在和中,
,
,
;
(2)平分,,
,,
,
,,
,
,
在中,,
,
,
平分,, ,
,
.
28.(1)解:如图1中,过点C作,垂足为M,则,
∵,
∴,,
∴,
∵是等腰三角形,,
∴,
在和中,,
∴,
∴,,
∵,,
∴,,
∴,,
∴,
∴;
(2)证明:设,则,
∵,,
∴,
由图2可知,等腰三角形中,,
∴,
∵,
∴,
∵,
,
∴,
∴,
∴,
∴;
(3)解:∵点C与点O重合,,
∴,
如图3,过点O作于点G,交的延长线于点H,与交于点M,
∵,
∴,
∵,,
∴,
又∵,,
∴,
∴,
又∵,,
∴平分,
∴,
∴.
29.(1)证明:∵都是等腰直角三角形,
∴,
∴,
∴,
∴;
(2)解:∵,
∴,
由(1)得:,
∵,
∴,
∴;
(3)解:过点F作于H,如图3所示:
∵是等腰直角三角形,,
∴,
∵,
∴,
∴,
∴,
同(1)得:,
∴,
∴,
∴,
∵,
∴,,,
∵,
∴是等边三角形,
∴,
∴
.
