第二十八章 锐角三角函数 复习课件(共19张PPT)数学人教版九年级下册
文档属性
| 名称 | 第二十八章 锐角三角函数 复习课件(共19张PPT)数学人教版九年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 829.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-24 18:27:42 | ||
图片预览





文档简介
(共19张PPT)
锐角三角函数
(复习课)
(新人教版)
一、本章知识结构梳理
锐角三角函数
1、锐角三角函数的定义
⑴、正弦;
⑵、余弦;
⑶、正切。
2、30°、45°、60°特殊角的三角函数值。
3、各锐角三角函数间的函数关系式
⑴、互余关系;
⑵、平方关系;
⑶、相除关系。
4、解直角三角形
⑴、定义;
⑵、直角三角形的性质
①、三边间关系;
②、锐角间关系;
③、边角间关系。
⑶、解直角三角形在实际问题中
的应用。
二、本章专题讲解
(一)知识专题讲解 专题一:锐角三角函数
专题概述:锐角三角函数的定义在解某些问题时可用作一种基本的方法。要熟练掌握特殊锐角的三角函数值,并理解常用的关系式:
对这些关系式要学会灵活运用
二、本章专题讲解
(一)知识专题讲解 专题一:锐角三角函数
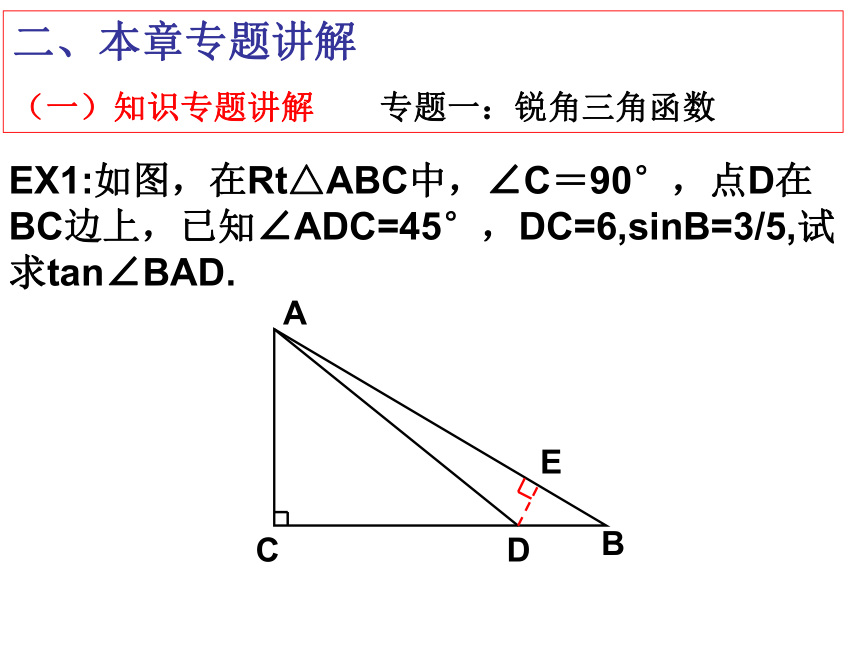
EX1:如图,在Rt△ABC中,∠C=90°,点D在BC边上,已知∠ADC=45°,DC=6,sinB=3/5,试求tan∠BAD.
A
C
B
D
E
二、本章专题讲解
(一)知识专题讲解 专题一:锐角三角函数
强化练习:
1、在△ABC中,∠C=90°,则sinA+cosA的值( )
A.等于1 B.大于1 C.小于1 D.不一定
2、若 无意义,则锐角 为( )
A.30° B.45° C.60° D.75°
B
A
二、本章专题讲解
(一)知识专题讲解 专题二:解直角三角形
专题概述:解直角三角形的知识在解决实际问题中有广泛的应用。因此要掌握直角三角形的一般解法,即已知一边一角和已知两边的两种情况,有时要与方程、不等式、相似三角形及圆等知识结合在一起,要注意各种方法的灵活运用。
二、本章专题讲解
(一)知识专题讲解 专题二:解直角三角形
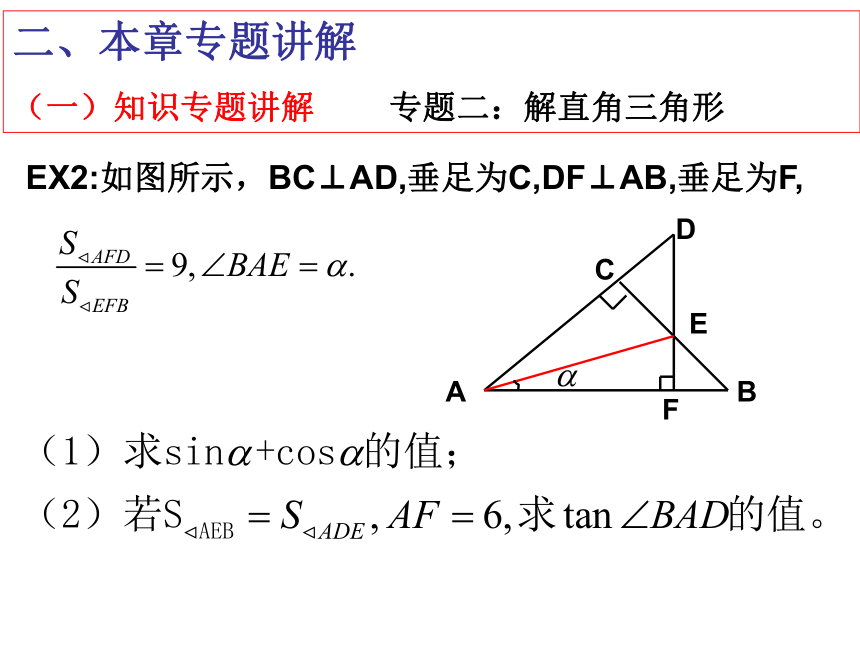
EX2:如图所示,BC⊥AD,垂足为C,DF⊥AB,垂足为F,
A
B
C
D
E
F
二、本章专题讲解
(一)知识专题讲解 专题二:解直角三角形
强化练习:
3、一辆汽车从立交桥头直行500m到达立交桥上25m高处,则这段斜坡的坡度是( )。
4、在△ABC中,∠A=30°,AC=40,BC=25,求
1︰
坡度
坡角:坡面与水平面的夹角叫做破角,用字母 表示。
坡度(坡比):坡面的铅
直高度h和水平距离l的
比叫做坡度,用字母 表
示,则
如图,坡度通常写成 的形式。
h
l
二、本章专题讲解
(一)知识专题讲解
专题三:解直角三角形的实际应用
专题概述:解直角三角形的知识在生活和生产中有广泛的应用,如在测量高度、距离、角度,确定方案时都常用到解直角三角形。解这类题关键是把实际问题转化为数学问题,常通过作辅助线构造直角三角形来解决。
二、本章专题讲解
(一)知识专题讲解
专题三:解直角三角形的实际应用
EX3:如图,为了测量某建筑物AB的高度,在平地上C处测的建筑物顶端A的仰角为30°,沿CB方向前进12m,到达D处,在D处测的建筑物顶点A的仰角为45°,则建筑物AB的高度等于( )。
D
A
B
C
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
二、本章专题讲解
(一)知识专题讲解
专题三:解直角三角形的实际应用
强化练习:
5、孩子们都喜欢荡秋千,如图,是一秋千示意图,当拉绳荡起偏离竖直位置30°角时,秋千低端的位置比原来升高了多少?(精确到0.1米)
O
A
B
10m
二、本章专题讲解
(二)思维方法专题讲解
专题四:解直角三角形的转化思想
专题概述:数学思想方法是数学的生命和灵魂。在本章的内容中,转化思想体现得特别突出。如求三角函数的值,三角函数关系中正弦和余弦的转化等,通常把问题转化到直角三角形中解决,在解直角三角形应用题时,把问题转化为解直角三角形的过程中体现了转化思想的数学价值。
二、本章专题讲解
(二)思维方法专题讲解
专题四:解直角三角形的转化思想
EX4:在△ABC中,AB=c,AC=b,BC=a,
请你证明
o
A
B
C
D
正弦定理
二、本章专题讲解
(二)思维方法专题讲解
专题四:解直角三角形的转化思想
强化练习:
6、如图,正方形ABCD中,M为DC的中点,N为BC上一点,BC=3NC,设∠MAN= 则 的值等于( )。
A
B
C
D
M
N
二、本章专题讲解
(二)思维方法专题讲解
专题四:解直角三角形的转化思想
强化练习:
7、课外实践活动中,数学老师带领学生测量学校旗杆的高度。如图,在A处用测角仪(离地面高度1.5m)测的旗杆顶端的仰角为15°,朝旗杆方向前进23m到达B处,再次测的旗杆顶角的仰角为30 °,求旗杆EG的高度。
A
B
C
D
E
F
G
13m
补充:
在△ABC中,若∠A、 ∠B、 ∠C的对边分别为a、b、c,则有结论:
余弦定理
海纳百川,有容乃大;
壁立千仞,无欲则刚。
锐角三角函数
(复习课)
(新人教版)
一、本章知识结构梳理
锐角三角函数
1、锐角三角函数的定义
⑴、正弦;
⑵、余弦;
⑶、正切。
2、30°、45°、60°特殊角的三角函数值。
3、各锐角三角函数间的函数关系式
⑴、互余关系;
⑵、平方关系;
⑶、相除关系。
4、解直角三角形
⑴、定义;
⑵、直角三角形的性质
①、三边间关系;
②、锐角间关系;
③、边角间关系。
⑶、解直角三角形在实际问题中
的应用。
二、本章专题讲解
(一)知识专题讲解 专题一:锐角三角函数
专题概述:锐角三角函数的定义在解某些问题时可用作一种基本的方法。要熟练掌握特殊锐角的三角函数值,并理解常用的关系式:
对这些关系式要学会灵活运用
二、本章专题讲解
(一)知识专题讲解 专题一:锐角三角函数
EX1:如图,在Rt△ABC中,∠C=90°,点D在BC边上,已知∠ADC=45°,DC=6,sinB=3/5,试求tan∠BAD.
A
C
B
D
E
二、本章专题讲解
(一)知识专题讲解 专题一:锐角三角函数
强化练习:
1、在△ABC中,∠C=90°,则sinA+cosA的值( )
A.等于1 B.大于1 C.小于1 D.不一定
2、若 无意义,则锐角 为( )
A.30° B.45° C.60° D.75°
B
A
二、本章专题讲解
(一)知识专题讲解 专题二:解直角三角形
专题概述:解直角三角形的知识在解决实际问题中有广泛的应用。因此要掌握直角三角形的一般解法,即已知一边一角和已知两边的两种情况,有时要与方程、不等式、相似三角形及圆等知识结合在一起,要注意各种方法的灵活运用。
二、本章专题讲解
(一)知识专题讲解 专题二:解直角三角形
EX2:如图所示,BC⊥AD,垂足为C,DF⊥AB,垂足为F,
A
B
C
D
E
F
二、本章专题讲解
(一)知识专题讲解 专题二:解直角三角形
强化练习:
3、一辆汽车从立交桥头直行500m到达立交桥上25m高处,则这段斜坡的坡度是( )。
4、在△ABC中,∠A=30°,AC=40,BC=25,求
1︰
坡度
坡角:坡面与水平面的夹角叫做破角,用字母 表示。
坡度(坡比):坡面的铅
直高度h和水平距离l的
比叫做坡度,用字母 表
示,则
如图,坡度通常写成 的形式。
h
l
二、本章专题讲解
(一)知识专题讲解
专题三:解直角三角形的实际应用
专题概述:解直角三角形的知识在生活和生产中有广泛的应用,如在测量高度、距离、角度,确定方案时都常用到解直角三角形。解这类题关键是把实际问题转化为数学问题,常通过作辅助线构造直角三角形来解决。
二、本章专题讲解
(一)知识专题讲解
专题三:解直角三角形的实际应用
EX3:如图,为了测量某建筑物AB的高度,在平地上C处测的建筑物顶端A的仰角为30°,沿CB方向前进12m,到达D处,在D处测的建筑物顶点A的仰角为45°,则建筑物AB的高度等于( )。
D
A
B
C
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
二、本章专题讲解
(一)知识专题讲解
专题三:解直角三角形的实际应用
强化练习:
5、孩子们都喜欢荡秋千,如图,是一秋千示意图,当拉绳荡起偏离竖直位置30°角时,秋千低端的位置比原来升高了多少?(精确到0.1米)
O
A
B
10m
二、本章专题讲解
(二)思维方法专题讲解
专题四:解直角三角形的转化思想
专题概述:数学思想方法是数学的生命和灵魂。在本章的内容中,转化思想体现得特别突出。如求三角函数的值,三角函数关系中正弦和余弦的转化等,通常把问题转化到直角三角形中解决,在解直角三角形应用题时,把问题转化为解直角三角形的过程中体现了转化思想的数学价值。
二、本章专题讲解
(二)思维方法专题讲解
专题四:解直角三角形的转化思想
EX4:在△ABC中,AB=c,AC=b,BC=a,
请你证明
o
A
B
C
D
正弦定理
二、本章专题讲解
(二)思维方法专题讲解
专题四:解直角三角形的转化思想
强化练习:
6、如图,正方形ABCD中,M为DC的中点,N为BC上一点,BC=3NC,设∠MAN= 则 的值等于( )。
A
B
C
D
M
N
二、本章专题讲解
(二)思维方法专题讲解
专题四:解直角三角形的转化思想
强化练习:
7、课外实践活动中,数学老师带领学生测量学校旗杆的高度。如图,在A处用测角仪(离地面高度1.5m)测的旗杆顶端的仰角为15°,朝旗杆方向前进23m到达B处,再次测的旗杆顶角的仰角为30 °,求旗杆EG的高度。
A
B
C
D
E
F
G
13m
补充:
在△ABC中,若∠A、 ∠B、 ∠C的对边分别为a、b、c,则有结论:
余弦定理
海纳百川,有容乃大;
壁立千仞,无欲则刚。
