初中数学人教版九年级下册第二十八章 锐角三角函数 复习课课件(共22张PPT)
文档属性
| 名称 | 初中数学人教版九年级下册第二十八章 锐角三角函数 复习课课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-24 19:07:03 | ||
图片预览




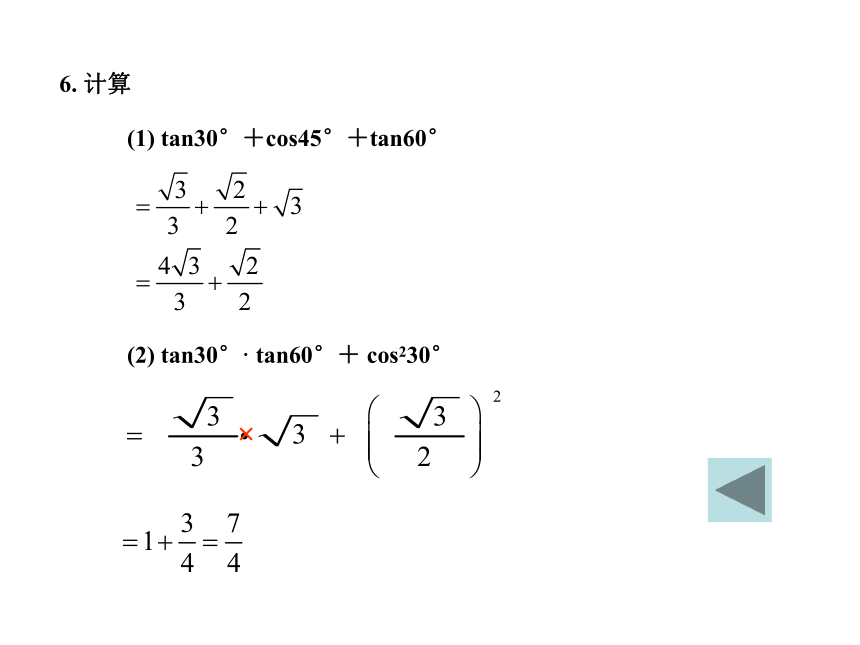

文档简介
(共22张PPT)
锐角三角函数
(复习课)
复习 目标
1.锐角三角函数的概念——基础
2.特殊角的三角函数值
(30°45°60°) ——熟记
3.锐角三角函数值的取值范围及增减性;互余两角的三角函数之间的关系__易错点
4.解直角三角形及在实际生活中应用——重点 (有关术语:仰角、俯角、方位角、坡角、坡度i)
一、本章知识结构梳理
锐角三角函数
1、锐角三角函数的定义
⑴、正弦;
⑵、余弦;
⑶、正切。
2、30°、45°、60°特殊角的三角函数值。
3、各锐角三角函数间关系
⑴、互余关系;
⑵、平方关系;
⑶、相除关系。
4、解直角三角形
⑴、定义;
⑵、两种类型
①、已知两边
②、已知一边一 角;
。
⑶、解直角三角形应用仰角 俯角 方位角 坡度 坡角
二 基础自测
1,在Rt△ABC中,如果各边都扩大2倍,则锐角A的正
弦值和余弦值( )
A,都不变 B,都扩大2倍 C,都缩小2倍 D,不确定。
√2
2
2,在△ABC中,若
sinA= ,tanB=√3,则∠C=
3, 在Rt△ABC中,
∠C=90°, AC= √3, AB=2,
Tan =
B
2
4,如果α和β都是锐角,且sinα= cosβ,
则α与β的关系 是( )
A,相等 B,互余 C,互补 D,不确定。
5.已知在Rt△ABC中, ∠C=90°,sinA= ,则 cosB=( )
1
2
√3
2
√2
2
2
1
√3
A, B, C, D,
A
75°
√3
3
B
A
(1) tan30°+cos45°+tan60°
(2) tan30°· tan60°+ cos230°
6. 计算
×
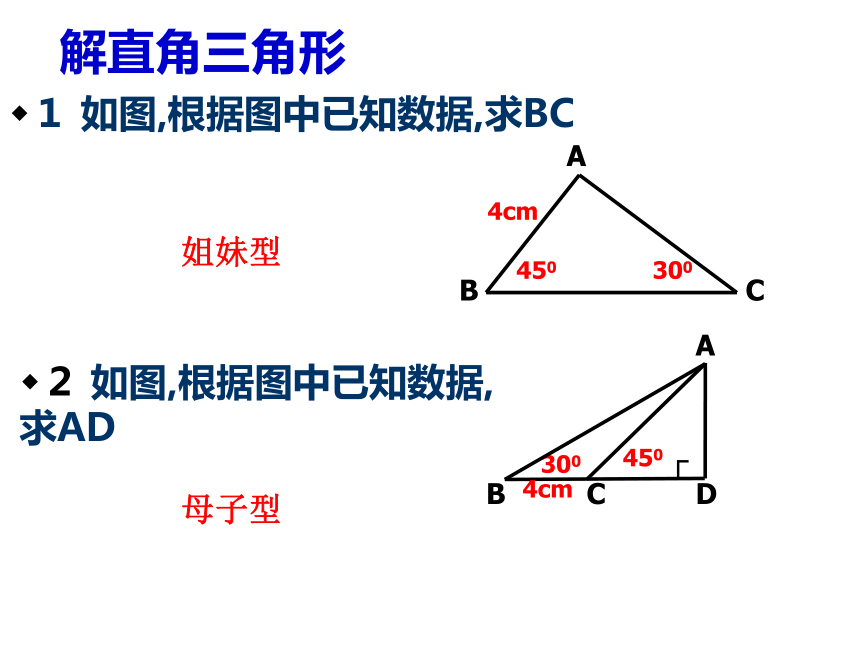
1 如图,根据图中已知数据,求BC
A
B
C
450
300
4cm
2 如图,根据图中已知数据, 求AD
A
B
C
450
300
4cm
D
┌
解直角三角形
姐妹型
母子型
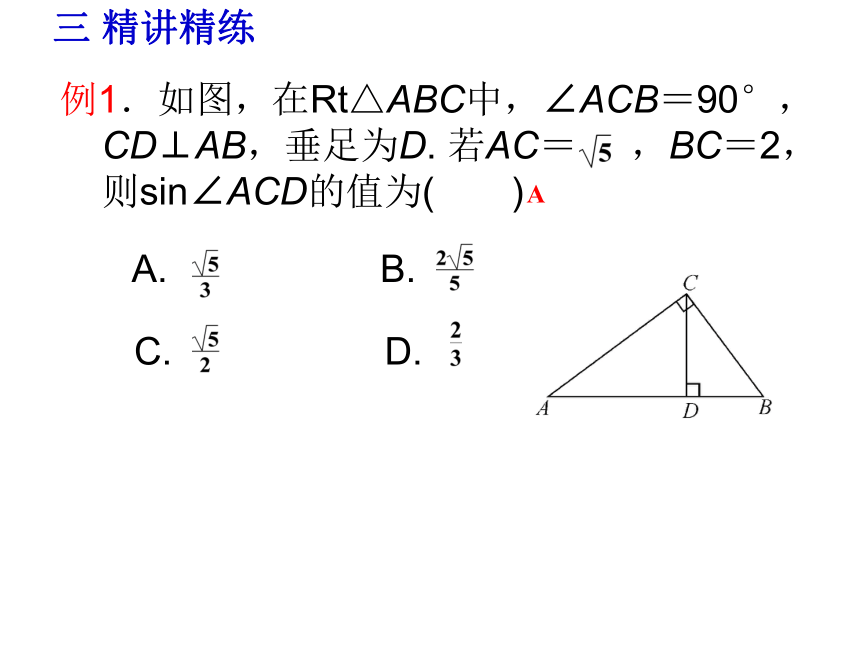
例1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D. 若AC= ,BC=2,则sin∠ACD的值为( )
A. B.
C. D.
A
三 精讲精练
例2、如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是
AC上一点,
若tan∠DBA=1/ 5,
求AD的长。
点拨:解三角函数题目最关键的是要构造合适的直角三角形,把已知角放在所构造的直角三角形中。本题已知tan∠DBA= ,所以可以过点D作DE⊥AB于E,把∠ DBA放于Rt△DBE中,然后根据正切函数的定义,即可弄清DE与BE的长度关系,再结合等腰Rt△的性质,此题就不难解答了。
1
5
C
D
A B
E
四 解直角三角形的实际应用
专题概述:解直角三角形的知识在生活和生产中有广泛的应用,如在测量问题、航行、坡度,求面积时都常用到解直角三角形。解这类题关键是把实际问题转化为数学问题,常通过作辅助线构造直角三角形来解决。
8分题
10分题
12分题
五 中考链接
综合实践课上,小明所在小组要测量护城河的宽度。如图所示是护城河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°。请你根据这些数据帮小明他们算出河宽FR(结果保留两位有效数字).
(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan36°≈0.73,sin 72°≈0.95,cos 72°≈0.31,tan72°≈3.08)
C
D
β
M
N
R
B
A
F
E
α
【解】过点F作FG∥EM交CD于G.
则MG=EF=20米.
∠FGN=∠α=36°.
∴∠GFN=∠β-∠FGN=72°-36°=36°.
∴∠FGN=∠GFN,
∴FN=GN=50-20=30(米).
在Rt△FNR中,
FR=FN×sinβ=30×sin72°=30×0.95≈29(米).
【思路分析】观察图形,此题需添加辅助线,将EM平移至点F处,构造直角三角形,从而利用解直角三角形的知识解决.
【方法规律】此题考查解直角三角形的应用. 解题关键是添加辅助线,构造直角三角形. 此题巧妙利用36°与72°之间的特殊关系,证明等腰三角形,从而简化了计算.
课堂小结
一个概念:锐角三角函数
两个基本类型:已知一边一角;或两边
两个基本图形:姐妹型,母子型
三个特殊角:30°45°60°
四种数学思想:转化,方程,数形结合,数 学建模。
五个数学术语:仰角,俯角,方位角,坡度,坡角
tana
cosa
sina
6 0°
45 °
3 0°
角 度
三角函数
1
角度
逐渐
增大
正弦值也增大
余弦值逐渐减小
正切值也随之增大
思 考
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1
0对这些关系式要学会灵活运用
坡度
坡角:坡面与水平面的夹角叫做坡角,用字母 表示。
坡度(坡比):坡面的铅
直高度h和水平距离l的
比叫做坡度,用字母 表
示,则
如图,坡度通常写成 的形式。
h
l
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
8分题
孩子们都喜欢荡秋千,如图,是一秋千示意图,当拉绳荡起偏离竖直位置30°角时,秋千低端的位置比原来升高了多少?(精确到0.1米)
O
A
B
10m
A
O
B
C
方法总结:对于这样的实际问题,先认真分析题意,建立直角三角形的模型,将实际问题转化为数学问题
10分:元旦期间,学校的教学楼上AC挂着庆元旦条幅BC,小明站在点F处,测得条幅顶端B的仰角为300,再往条幅方向前进20m到达点E处,测得B的仰角为600,求条幅BC的长。
1、如果设BC=x,那么CF是多少?
CF=
2、CE可以怎样表示?
3、CE和CF有怎样的数量
关系?
4、这道题还可以怎样解?
你能找出EF和EB的关系吗?
12分题 如图,一航船在A处测到北偏东450方向上有一灯塔B,航船向正东方向以20海里/h的速度航行1.5h到达C处时,又测得灯塔B在北偏东150方向上,求此时航船与灯塔相距多少海里?
D
东
北
15
°
45
°
C
B
A
E
1、这道题应如何添辅助线?
如果过B作AC的垂线,有什么问题?
2、请说一说这道题如何解?
中考链接
星期天,小强去水库大坝游玩,他站在大坝上的A处看到一棵大树的影子刚好落在坝底的B处(点A与大树及其影子在同一平面内),此时太阳光与地面成60°角.在A处测得树顶D的俯角为15°.如图所示,已知AB与地面的夹角为60°,AB为8米.请你帮助小强计算一下这颗大树的高度?(结果精确到1米.参考数据 √2 ≈1.4 √3 ≈1.7)
锐角三角函数
(复习课)
复习 目标
1.锐角三角函数的概念——基础
2.特殊角的三角函数值
(30°45°60°) ——熟记
3.锐角三角函数值的取值范围及增减性;互余两角的三角函数之间的关系__易错点
4.解直角三角形及在实际生活中应用——重点 (有关术语:仰角、俯角、方位角、坡角、坡度i)
一、本章知识结构梳理
锐角三角函数
1、锐角三角函数的定义
⑴、正弦;
⑵、余弦;
⑶、正切。
2、30°、45°、60°特殊角的三角函数值。
3、各锐角三角函数间关系
⑴、互余关系;
⑵、平方关系;
⑶、相除关系。
4、解直角三角形
⑴、定义;
⑵、两种类型
①、已知两边
②、已知一边一 角;
。
⑶、解直角三角形应用仰角 俯角 方位角 坡度 坡角
二 基础自测
1,在Rt△ABC中,如果各边都扩大2倍,则锐角A的正
弦值和余弦值( )
A,都不变 B,都扩大2倍 C,都缩小2倍 D,不确定。
√2
2
2,在△ABC中,若
sinA= ,tanB=√3,则∠C=
3, 在Rt△ABC中,
∠C=90°, AC= √3, AB=2,
Tan =
B
2
4,如果α和β都是锐角,且sinα= cosβ,
则α与β的关系 是( )
A,相等 B,互余 C,互补 D,不确定。
5.已知在Rt△ABC中, ∠C=90°,sinA= ,则 cosB=( )
1
2
√3
2
√2
2
2
1
√3
A, B, C, D,
A
75°
√3
3
B
A
(1) tan30°+cos45°+tan60°
(2) tan30°· tan60°+ cos230°
6. 计算
×
1 如图,根据图中已知数据,求BC
A
B
C
450
300
4cm
2 如图,根据图中已知数据, 求AD
A
B
C
450
300
4cm
D
┌
解直角三角形
姐妹型
母子型
例1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D. 若AC= ,BC=2,则sin∠ACD的值为( )
A. B.
C. D.
A
三 精讲精练
例2、如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是
AC上一点,
若tan∠DBA=1/ 5,
求AD的长。
点拨:解三角函数题目最关键的是要构造合适的直角三角形,把已知角放在所构造的直角三角形中。本题已知tan∠DBA= ,所以可以过点D作DE⊥AB于E,把∠ DBA放于Rt△DBE中,然后根据正切函数的定义,即可弄清DE与BE的长度关系,再结合等腰Rt△的性质,此题就不难解答了。
1
5
C
D
A B
E
四 解直角三角形的实际应用
专题概述:解直角三角形的知识在生活和生产中有广泛的应用,如在测量问题、航行、坡度,求面积时都常用到解直角三角形。解这类题关键是把实际问题转化为数学问题,常通过作辅助线构造直角三角形来解决。
8分题
10分题
12分题
五 中考链接
综合实践课上,小明所在小组要测量护城河的宽度。如图所示是护城河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°。请你根据这些数据帮小明他们算出河宽FR(结果保留两位有效数字).
(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan36°≈0.73,sin 72°≈0.95,cos 72°≈0.31,tan72°≈3.08)
C
D
β
M
N
R
B
A
F
E
α
【解】过点F作FG∥EM交CD于G.
则MG=EF=20米.
∠FGN=∠α=36°.
∴∠GFN=∠β-∠FGN=72°-36°=36°.
∴∠FGN=∠GFN,
∴FN=GN=50-20=30(米).
在Rt△FNR中,
FR=FN×sinβ=30×sin72°=30×0.95≈29(米).
【思路分析】观察图形,此题需添加辅助线,将EM平移至点F处,构造直角三角形,从而利用解直角三角形的知识解决.
【方法规律】此题考查解直角三角形的应用. 解题关键是添加辅助线,构造直角三角形. 此题巧妙利用36°与72°之间的特殊关系,证明等腰三角形,从而简化了计算.
课堂小结
一个概念:锐角三角函数
两个基本类型:已知一边一角;或两边
两个基本图形:姐妹型,母子型
三个特殊角:30°45°60°
四种数学思想:转化,方程,数形结合,数 学建模。
五个数学术语:仰角,俯角,方位角,坡度,坡角
tana
cosa
sina
6 0°
45 °
3 0°
角 度
三角函数
1
角度
逐渐
增大
正弦值也增大
余弦值逐渐减小
正切值也随之增大
思 考
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1
0
坡度
坡角:坡面与水平面的夹角叫做坡角,用字母 表示。
坡度(坡比):坡面的铅
直高度h和水平距离l的
比叫做坡度,用字母 表
示,则
如图,坡度通常写成 的形式。
h
l
仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
8分题
孩子们都喜欢荡秋千,如图,是一秋千示意图,当拉绳荡起偏离竖直位置30°角时,秋千低端的位置比原来升高了多少?(精确到0.1米)
O
A
B
10m
A
O
B
C
方法总结:对于这样的实际问题,先认真分析题意,建立直角三角形的模型,将实际问题转化为数学问题
10分:元旦期间,学校的教学楼上AC挂着庆元旦条幅BC,小明站在点F处,测得条幅顶端B的仰角为300,再往条幅方向前进20m到达点E处,测得B的仰角为600,求条幅BC的长。
1、如果设BC=x,那么CF是多少?
CF=
2、CE可以怎样表示?
3、CE和CF有怎样的数量
关系?
4、这道题还可以怎样解?
你能找出EF和EB的关系吗?
12分题 如图,一航船在A处测到北偏东450方向上有一灯塔B,航船向正东方向以20海里/h的速度航行1.5h到达C处时,又测得灯塔B在北偏东150方向上,求此时航船与灯塔相距多少海里?
D
东
北
15
°
45
°
C
B
A
E
1、这道题应如何添辅助线?
如果过B作AC的垂线,有什么问题?
2、请说一说这道题如何解?
中考链接
星期天,小强去水库大坝游玩,他站在大坝上的A处看到一棵大树的影子刚好落在坝底的B处(点A与大树及其影子在同一平面内),此时太阳光与地面成60°角.在A处测得树顶D的俯角为15°.如图所示,已知AB与地面的夹角为60°,AB为8米.请你帮助小强计算一下这颗大树的高度?(结果精确到1米.参考数据 √2 ≈1.4 √3 ≈1.7)
