第二十章(5)数据的分析—八年级下册人教版数学优选100题(含答案)
文档属性
| 名称 | 第二十章(5)数据的分析—八年级下册人教版数学优选100题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 753.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-23 23:42:29 | ||
图片预览




文档简介
(5)数据的分析—八年级下册人教版数学优选100题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某次校运会共有13名同学报名参加百米赛跑,他们的预赛成绩各不相同,现取其中前6名参加决赛,小勇同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这13名同学成绩的( )
A.平均数 B.众数 C.中位数 D.方差
2.下表记录了四位射击运动员选拔比赛成绩的平均数和方差:
运动员 甲 乙 丙 丁
平均数(环)
方差(环)
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
3.某同学对数据26,36,46,5□,57进行统计分析,发现其中一个两位数的个位数字缺失,则以下计算结果与该数字无关的是( )
A.平均数 B.众数 C.中位数 D.方差
4.在一列数1,8,x,4,9,4,11中,众数是4,平均数是7,中位数是8,则数x是( )
A.3 B.6 C.9 D.
5.某次测试结束,嘉琪随机抽取了九(1)班学生的成绩进行统计,并绘制成如图所示的扇形统计图,则该班学生的平均成绩为( )
A.9分 B.分 C.分 D.8分
6.若样本,,,的平均数为10,方差为2,则对于样本,,…,,下列结论正确的是( )
A.平均数为10,方差为2 B.平均数为11,方差为3
C.平均数为12,方差为2 D.平均数为12,方差为4
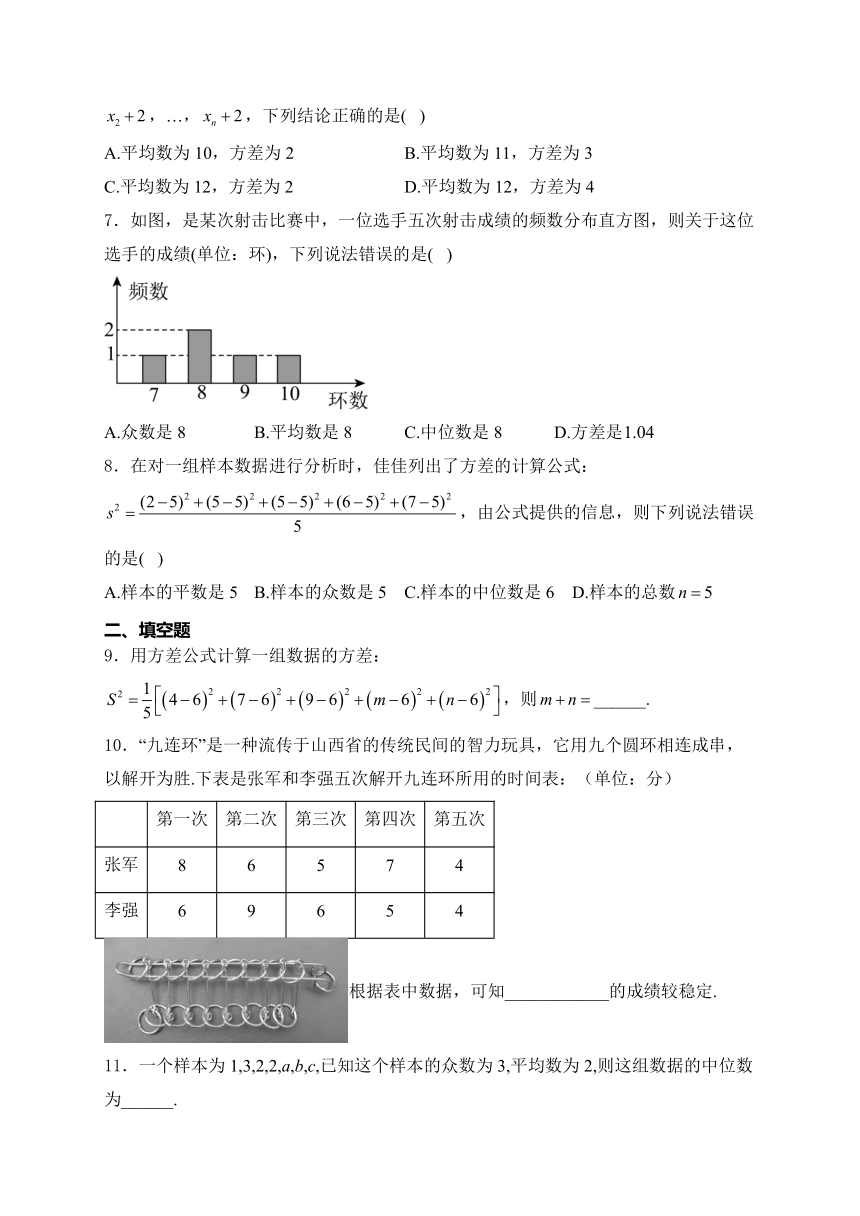
7.如图,是某次射击比赛中,一位选手五次射击成绩的频数分布直方图,则关于这位选手的成绩(单位:环),下列说法错误的是( )
A.众数是8 B.平均数是8 C.中位数是8 D.方差是
8.在对一组样本数据进行分析时,佳佳列出了方差的计算公式:,由公式提供的信息,则下列说法错误的是( )
A.样本的平数是5 B.样本的众数是5 C.样本的中位数是6 D.样本的总数
二、填空题
9.用方差公式计算一组数据的方差:,则______.
10.“九连环”是一种流传于山西省的传统民间的智力玩具,它用九个圆环相连成串,以解开为胜.下表是张军和李强五次解开九连环所用的时间表:(单位:分)
第一次 第二次 第三次 第四次 第五次
张军 8 6 5 7 4
李强 6 9 6 5 4
根据表中数据,可知____________的成绩较稳定.
11.一个样本为1,3,2,2,a,b,c,已知这个样本的众数为3,平均数为2,则这组数据的中位数为______.
12.某中学田径队名队员的运动鞋鞋码与相应的人数如下表:
鞋码
人数 5 x y 4 2
则这名队员鞋码的众数是_________.
三、解答题
13.某公司计划招聘一名大学毕业生做科研助理,组织了一场面试,甲、乙两个大学生的成绩如下表(单位:分):
应聘大学生 仪表形象 语言表达 专业知识 实验水平
甲 96 88 80 84
乙 86 92 86 88
(1)乙的四项得分的众数为______分,中位数为______分.
(2)若将仪表形象、语言表达、专业知识、实验水平四项得分按的比例确定最终录用人选,通过计算说明若只看最终成绩,该公司会录用哪个大学生.
(3)请你判断(2)中分配比例是否合理.若合理,请说明理由;若不合理,请给出一个你认为合理的比例,并给出理由.
14.学校组织七、八年级学生参加了“国家安全知识”测试(满分100分).已知七、八年级各有200人,现从两个年级分别随机抽取10名学生的测试成绩(单位:分)进行统计:
七年级86,94,79,84,71,90,76,83,90,87
八年级88,76,90,78,87,93,75,87,87,79
整理如下:
年级 平均数 中位数 众数 方差
七年级 84 90
八年级 84 87
根据以上信息,回答下列问题:
(1)填空:_______,________.
同学说:“这次测试我得了86分,位于年级中等偏上水平”,由此可判断他是________年级的学生;
(2)学校规定测试成绩不低于85分为“优秀”,估计该校这两个年级测试成绩达到“优秀”的学生总人数;
(3)你认为哪个年级的学生掌握国家安全知识的总体水平较好?请给出一条理由.
15.熊猫作为我国独有的珍稀动物,因其萌态可掬深受全世界人们的喜爱.成都大熊猫繁育研究基地的“和花、和叶”,重庆动物园的“渝可、渝爱”,北京动物园的“萌兰”等被称为“熊猫界的顶流”倍受人们的关注.某校举办了“珍爱自然,珍爱熊猫,共创美好家园”的知识竞赛,从该校七、八年级中各随机抽取10名学生的成绩(百分制,单位:分)进行整理、描述和分析(成绩得分用表示,共分成四组;;;).下面给出了部分信息:
七年级10名学生的成绩是:82,86,87,88,89,93,93,94,98,100.
八年级10名学生的成绩在组中的数据是:91,94,93,92.
八年级抽取的学生成绩扇形统计图:
七、八年级抽取的学生成绩统计表:
平均数 中位数 众数 方差
七年级 91 91 29.8
八年级 91 95 17.8
根据以上信息,解答下列问题:
(1)填空:______,______,______;
(2)根据以上数据.你认为该校七年级和八年级中哪个年级学生掌握知识较好?请说明理由(一条即可);
(3)已知该校七年级有800人,八年级有900人参加了此次知识竞赛活动,请估计两个年级参加竞赛活动的成绩不低于90分的共有多少人?
16.为推动全民阅读、建设书香社会、增强青少年的爱国情感.某校举办“阅读红色经典,讲好思政故事”主题演讲活动.本次活动共有30名学生进入决赛.七名评委从演讲内容、语言表达、形象风度、综合印象四项对参赛选手评分、去掉一个最高分和一个最低分后取平均分得到每项成绩.再将演讲内容.语言表达、形象风度、综合印象四项成绩按的比例计算出每人的最终成绩.小蕊,小迪的四项成绩和最终成绩如下表,30名学生最终成绩绘制成的频数直方图(每组包含最小值,不包含最大值)如下图.
小蕊、小迪的四项成绩和最终成绩统计表
选手 四项成绩/分 最终成绩/分
演讲内容 语言表达 形象风度 综合印象
小蕊 97 96 90 94 95
小迪 88 83 85
请根据上述信息,解答下列问题:
(1)七名评委给小迪的演讲内容打分分别为87、85、91、94、91、88、93.去掉一个最高分和一个最低分,剩余数据的中位数是________分,众数是________分,平均数是________分.
(2)请你计算小迪的最终成绩.
(3)学校决定根据最终成绩从高到低设立一等奖、二等奖、三等奖、优秀奖,占比分别为,、、.请你判断小蕊和小迪分别获几等奖,并说明理由.
参考答案
1.答案:C
解析:共有13名学生参加比赛,取前6名,所以小勇需要知道自己的成绩是否进入前六.
我们把所有同学的成绩按大小顺序排列,第7名学生的成绩是这组数据的中位数,
所以小勇知道这组数据的中位数,才能知道自己是否进入决赛.
故选:C.
2.答案:D
解析:∵乙和丁的平均数较大,
∴从乙和丁中选择一人参加竞赛,
∵丁的方差较小,
∴选择丁参加比赛,
故选:D.
3.答案:C
解析:这组数据的平均数、方差和众数都与第4个数有关,而这组数据的中位数为46,与第4个数无关.
故答案为:C.
4.答案:D
解析:这组数据中的平均数是7,
,
解得:,
故选:D.
5.答案:A
解析:平均成绩为:
(分).
故选A.
6.答案:C
解析:样本,,…,,对于样本,,,来说,每个数据均在原来的基础上增加了2,
根据平均数、方差的变化规律得:平均数较前增加2,而方差不变,
即:平均数为,方差为2,
故选:C.
7.答案:B
解析:由频数分布直方图得:该选手五次射击的成绩为7,8,8,9,10
则众数是8
平均数是
中位数是8
方差是
故选:B.
8.答案:C
解析:由方差的计算公式知,这组数据为2、5、5、6、7,
所以这组数据的样本容量为5,中位数为5,众数为5,
平均数为:,样本的总数,
故样本的中位数是6错误,
故选:C.
9.答案:10
解析:,
,
.
故答案为:10.
10.答案:张军
解析:由题中表格可知,
张军用时平均值为;
李强用时平均值为;
从平均值来看,张军和李强的成绩稳定性相同;
张军用时方差为;
李强用时方差为;
,
从方差来看,张军的成绩比李强稳定,
故答案为:张军.
11.答案:2
解析:因为众数为3,可设,,c未知,
平均数,
解得,
将这组数据按从小到大的顺序排列:0,1,2,2,3,3,3,
位于最中间的一个数是2,所以中位数是2,
故答案为:2.
12.答案:或或和
解析:因为共有人,所以,
若,则众数为;
若,则众数为;
若,则众数为和
综上所述,众数是或或和,
故答案为:或或和.
13.答案:(1)86,87
(2)甲
(3)不合理,我认为合理的比例为:,理由见解析
解析:(1)乙的四项得分从小到大依次排序为:86,86,88,92,
故乙的四项得分的众数为86分,中位数为分,
故答案为:86,87;
(2)(分),
(分),
,
该公司会录用甲;
(3)不合理,理由:
科研助理更加注重专业知识、实验水平,仪表形象、语言表达占比应减小.
我认为合理的比例为:,这样专业知识、实验水平的比例更重.
14.答案:(1)85,87,七
(2)220
(3)八年级,理由见解析
解析:(1)把七年级10名学生的测试成绩排好顺序为:71,76,79,83,84,86,87,90,90,94,
根据中位数的定义可知,该组数据的中位数为,
八年级10名学生的成绩中87分的最多有3人,所以众数,
A同学得了86分大于85分,位于年级中等偏上水平,由此可判断他是七年级的学生;
故答案为:85,87,七;
(2)(人),
答:该校这两个年级测试成绩达到“优秀”的学生总人数为220人;
(3)我认为八年级的学生掌握国家安全知识的总体水平较好,
理由:因为七、八年级测试成绩的平均数相等,八年级测试成绩的方差小于七年级测试成绩的方差,所以八年级的学生掌握防震减灾科普知识的总体水平较好.
15.答案:(1),,;
(2)八年级学生掌握知识较好,理由见解答(答案不唯一);
(3)两个年级参加竞赛活动的成绩不低于90分的共有人.
解析:(1)由题知,八年级组所占百分比为:.
八年级组所占百分比为:,
,
七年级10名学生的成绩中出现次数最多,
,
由中位数定义可知;
故答案为:,,;
(2)八年级学生掌握知识较好,
由表格知,八年级学生成绩的平均数与七年级相等,而八年级学生成绩的方差小于七年级,所以八年级学生成绩更加稳定(答案不唯一);
(3)七年级成绩不低于90分的有:(人);
八年级成绩不低于90分的:(人);
(人);
答:两个年级参加竞赛活动的成绩不低于90分的共有人.
16.答案:(1)91;91;90
(2)
(3)小蕊获一等奖,小迪获三等奖
解析:(1)从小到大排列为:85、87、、91、91、93、94,去掉一个最高分和一个最低分,剩余数据为87、、91、91、93
中位数为91,众数是91分,平均数是(分)
故答案为:91;91;90.
(2)
(3)小蕊获一等奖,小迪获三等奖.
理由:获一等奖的学生有(名),由频数直方图可知,最终成绩不低于95分且小于100分的学生有2名,
小蕊最终成绩95分在这一组,因此小蕊获一等奖;
获一、二等奖的学生共有(名),
获三等奖的学生有(名),由频数直方图可知,最终成绩不低于90分的学生获一等奖或二等奖,最终成绩不低于85分且小于90分的学生有9名,均获三等奖.又因为小迪最终成绩为分,所以小迪获三等奖.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某次校运会共有13名同学报名参加百米赛跑,他们的预赛成绩各不相同,现取其中前6名参加决赛,小勇同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这13名同学成绩的( )
A.平均数 B.众数 C.中位数 D.方差
2.下表记录了四位射击运动员选拔比赛成绩的平均数和方差:
运动员 甲 乙 丙 丁
平均数(环)
方差(环)
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
3.某同学对数据26,36,46,5□,57进行统计分析,发现其中一个两位数的个位数字缺失,则以下计算结果与该数字无关的是( )
A.平均数 B.众数 C.中位数 D.方差
4.在一列数1,8,x,4,9,4,11中,众数是4,平均数是7,中位数是8,则数x是( )
A.3 B.6 C.9 D.
5.某次测试结束,嘉琪随机抽取了九(1)班学生的成绩进行统计,并绘制成如图所示的扇形统计图,则该班学生的平均成绩为( )
A.9分 B.分 C.分 D.8分
6.若样本,,,的平均数为10,方差为2,则对于样本,,…,,下列结论正确的是( )
A.平均数为10,方差为2 B.平均数为11,方差为3
C.平均数为12,方差为2 D.平均数为12,方差为4
7.如图,是某次射击比赛中,一位选手五次射击成绩的频数分布直方图,则关于这位选手的成绩(单位:环),下列说法错误的是( )
A.众数是8 B.平均数是8 C.中位数是8 D.方差是
8.在对一组样本数据进行分析时,佳佳列出了方差的计算公式:,由公式提供的信息,则下列说法错误的是( )
A.样本的平数是5 B.样本的众数是5 C.样本的中位数是6 D.样本的总数
二、填空题
9.用方差公式计算一组数据的方差:,则______.
10.“九连环”是一种流传于山西省的传统民间的智力玩具,它用九个圆环相连成串,以解开为胜.下表是张军和李强五次解开九连环所用的时间表:(单位:分)
第一次 第二次 第三次 第四次 第五次
张军 8 6 5 7 4
李强 6 9 6 5 4
根据表中数据,可知____________的成绩较稳定.
11.一个样本为1,3,2,2,a,b,c,已知这个样本的众数为3,平均数为2,则这组数据的中位数为______.
12.某中学田径队名队员的运动鞋鞋码与相应的人数如下表:
鞋码
人数 5 x y 4 2
则这名队员鞋码的众数是_________.
三、解答题
13.某公司计划招聘一名大学毕业生做科研助理,组织了一场面试,甲、乙两个大学生的成绩如下表(单位:分):
应聘大学生 仪表形象 语言表达 专业知识 实验水平
甲 96 88 80 84
乙 86 92 86 88
(1)乙的四项得分的众数为______分,中位数为______分.
(2)若将仪表形象、语言表达、专业知识、实验水平四项得分按的比例确定最终录用人选,通过计算说明若只看最终成绩,该公司会录用哪个大学生.
(3)请你判断(2)中分配比例是否合理.若合理,请说明理由;若不合理,请给出一个你认为合理的比例,并给出理由.
14.学校组织七、八年级学生参加了“国家安全知识”测试(满分100分).已知七、八年级各有200人,现从两个年级分别随机抽取10名学生的测试成绩(单位:分)进行统计:
七年级86,94,79,84,71,90,76,83,90,87
八年级88,76,90,78,87,93,75,87,87,79
整理如下:
年级 平均数 中位数 众数 方差
七年级 84 90
八年级 84 87
根据以上信息,回答下列问题:
(1)填空:_______,________.
同学说:“这次测试我得了86分,位于年级中等偏上水平”,由此可判断他是________年级的学生;
(2)学校规定测试成绩不低于85分为“优秀”,估计该校这两个年级测试成绩达到“优秀”的学生总人数;
(3)你认为哪个年级的学生掌握国家安全知识的总体水平较好?请给出一条理由.
15.熊猫作为我国独有的珍稀动物,因其萌态可掬深受全世界人们的喜爱.成都大熊猫繁育研究基地的“和花、和叶”,重庆动物园的“渝可、渝爱”,北京动物园的“萌兰”等被称为“熊猫界的顶流”倍受人们的关注.某校举办了“珍爱自然,珍爱熊猫,共创美好家园”的知识竞赛,从该校七、八年级中各随机抽取10名学生的成绩(百分制,单位:分)进行整理、描述和分析(成绩得分用表示,共分成四组;;;).下面给出了部分信息:
七年级10名学生的成绩是:82,86,87,88,89,93,93,94,98,100.
八年级10名学生的成绩在组中的数据是:91,94,93,92.
八年级抽取的学生成绩扇形统计图:
七、八年级抽取的学生成绩统计表:
平均数 中位数 众数 方差
七年级 91 91 29.8
八年级 91 95 17.8
根据以上信息,解答下列问题:
(1)填空:______,______,______;
(2)根据以上数据.你认为该校七年级和八年级中哪个年级学生掌握知识较好?请说明理由(一条即可);
(3)已知该校七年级有800人,八年级有900人参加了此次知识竞赛活动,请估计两个年级参加竞赛活动的成绩不低于90分的共有多少人?
16.为推动全民阅读、建设书香社会、增强青少年的爱国情感.某校举办“阅读红色经典,讲好思政故事”主题演讲活动.本次活动共有30名学生进入决赛.七名评委从演讲内容、语言表达、形象风度、综合印象四项对参赛选手评分、去掉一个最高分和一个最低分后取平均分得到每项成绩.再将演讲内容.语言表达、形象风度、综合印象四项成绩按的比例计算出每人的最终成绩.小蕊,小迪的四项成绩和最终成绩如下表,30名学生最终成绩绘制成的频数直方图(每组包含最小值,不包含最大值)如下图.
小蕊、小迪的四项成绩和最终成绩统计表
选手 四项成绩/分 最终成绩/分
演讲内容 语言表达 形象风度 综合印象
小蕊 97 96 90 94 95
小迪 88 83 85
请根据上述信息,解答下列问题:
(1)七名评委给小迪的演讲内容打分分别为87、85、91、94、91、88、93.去掉一个最高分和一个最低分,剩余数据的中位数是________分,众数是________分,平均数是________分.
(2)请你计算小迪的最终成绩.
(3)学校决定根据最终成绩从高到低设立一等奖、二等奖、三等奖、优秀奖,占比分别为,、、.请你判断小蕊和小迪分别获几等奖,并说明理由.
参考答案
1.答案:C
解析:共有13名学生参加比赛,取前6名,所以小勇需要知道自己的成绩是否进入前六.
我们把所有同学的成绩按大小顺序排列,第7名学生的成绩是这组数据的中位数,
所以小勇知道这组数据的中位数,才能知道自己是否进入决赛.
故选:C.
2.答案:D
解析:∵乙和丁的平均数较大,
∴从乙和丁中选择一人参加竞赛,
∵丁的方差较小,
∴选择丁参加比赛,
故选:D.
3.答案:C
解析:这组数据的平均数、方差和众数都与第4个数有关,而这组数据的中位数为46,与第4个数无关.
故答案为:C.
4.答案:D
解析:这组数据中的平均数是7,
,
解得:,
故选:D.
5.答案:A
解析:平均成绩为:
(分).
故选A.
6.答案:C
解析:样本,,…,,对于样本,,,来说,每个数据均在原来的基础上增加了2,
根据平均数、方差的变化规律得:平均数较前增加2,而方差不变,
即:平均数为,方差为2,
故选:C.
7.答案:B
解析:由频数分布直方图得:该选手五次射击的成绩为7,8,8,9,10
则众数是8
平均数是
中位数是8
方差是
故选:B.
8.答案:C
解析:由方差的计算公式知,这组数据为2、5、5、6、7,
所以这组数据的样本容量为5,中位数为5,众数为5,
平均数为:,样本的总数,
故样本的中位数是6错误,
故选:C.
9.答案:10
解析:,
,
.
故答案为:10.
10.答案:张军
解析:由题中表格可知,
张军用时平均值为;
李强用时平均值为;
从平均值来看,张军和李强的成绩稳定性相同;
张军用时方差为;
李强用时方差为;
,
从方差来看,张军的成绩比李强稳定,
故答案为:张军.
11.答案:2
解析:因为众数为3,可设,,c未知,
平均数,
解得,
将这组数据按从小到大的顺序排列:0,1,2,2,3,3,3,
位于最中间的一个数是2,所以中位数是2,
故答案为:2.
12.答案:或或和
解析:因为共有人,所以,
若,则众数为;
若,则众数为;
若,则众数为和
综上所述,众数是或或和,
故答案为:或或和.
13.答案:(1)86,87
(2)甲
(3)不合理,我认为合理的比例为:,理由见解析
解析:(1)乙的四项得分从小到大依次排序为:86,86,88,92,
故乙的四项得分的众数为86分,中位数为分,
故答案为:86,87;
(2)(分),
(分),
,
该公司会录用甲;
(3)不合理,理由:
科研助理更加注重专业知识、实验水平,仪表形象、语言表达占比应减小.
我认为合理的比例为:,这样专业知识、实验水平的比例更重.
14.答案:(1)85,87,七
(2)220
(3)八年级,理由见解析
解析:(1)把七年级10名学生的测试成绩排好顺序为:71,76,79,83,84,86,87,90,90,94,
根据中位数的定义可知,该组数据的中位数为,
八年级10名学生的成绩中87分的最多有3人,所以众数,
A同学得了86分大于85分,位于年级中等偏上水平,由此可判断他是七年级的学生;
故答案为:85,87,七;
(2)(人),
答:该校这两个年级测试成绩达到“优秀”的学生总人数为220人;
(3)我认为八年级的学生掌握国家安全知识的总体水平较好,
理由:因为七、八年级测试成绩的平均数相等,八年级测试成绩的方差小于七年级测试成绩的方差,所以八年级的学生掌握防震减灾科普知识的总体水平较好.
15.答案:(1),,;
(2)八年级学生掌握知识较好,理由见解答(答案不唯一);
(3)两个年级参加竞赛活动的成绩不低于90分的共有人.
解析:(1)由题知,八年级组所占百分比为:.
八年级组所占百分比为:,
,
七年级10名学生的成绩中出现次数最多,
,
由中位数定义可知;
故答案为:,,;
(2)八年级学生掌握知识较好,
由表格知,八年级学生成绩的平均数与七年级相等,而八年级学生成绩的方差小于七年级,所以八年级学生成绩更加稳定(答案不唯一);
(3)七年级成绩不低于90分的有:(人);
八年级成绩不低于90分的:(人);
(人);
答:两个年级参加竞赛活动的成绩不低于90分的共有人.
16.答案:(1)91;91;90
(2)
(3)小蕊获一等奖,小迪获三等奖
解析:(1)从小到大排列为:85、87、、91、91、93、94,去掉一个最高分和一个最低分,剩余数据为87、、91、91、93
中位数为91,众数是91分,平均数是(分)
故答案为:91;91;90.
(2)
(3)小蕊获一等奖,小迪获三等奖.
理由:获一等奖的学生有(名),由频数直方图可知,最终成绩不低于95分且小于100分的学生有2名,
小蕊最终成绩95分在这一组,因此小蕊获一等奖;
获一、二等奖的学生共有(名),
获三等奖的学生有(名),由频数直方图可知,最终成绩不低于90分的学生获一等奖或二等奖,最终成绩不低于85分且小于90分的学生有9名,均获三等奖.又因为小迪最终成绩为分,所以小迪获三等奖.
