第十七章(2)勾股定理—八年级下册人教版数学优选100题(含答案)
文档属性
| 名称 | 第十七章(2)勾股定理—八年级下册人教版数学优选100题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-23 00:00:00 | ||
图片预览


文档简介
(2)勾股定理—八年级下册人教版数学优选100题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列命题的逆命题成立的是( )
A.全等三角形的对应角相等
B.同位角互补,两直线平行
C.对顶角相等
D.若三角形三边满足,则该三角形是直角三角形
2.下列四组线段不能围成直角三角形的是( )
A.,, B.,,
C.,, D.,,
3.若的三边分别为,,,且满足,则是( )
A.以为斜边的直角三角形 B.以为斜边的直角三角形
C.以为斜边的直角三角形 D.不是直角三角形
4.如图所示,,,若数轴上点A所表示的数为a,则a的值为( )
A. B. C. D.
5.如图,在中,,若,则正方形和正方形的面积之和为( )
A. B. C. D.
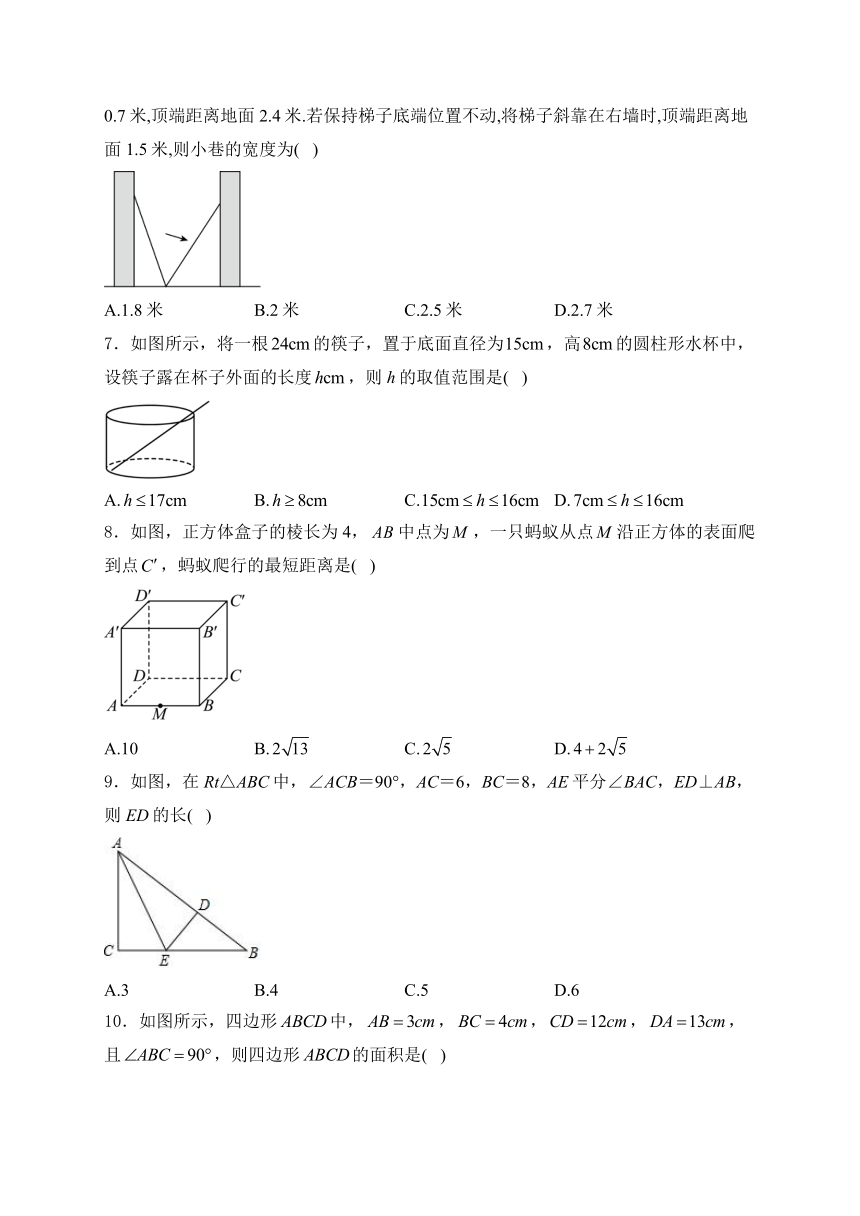
6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙的距离为0.7米,顶端距离地面2.4米.若保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面1.5米,则小巷的宽度为( )
A.1.8米 B.2米 C.2.5米 D.2.7米
7.如图所示,将一根的筷子,置于底面直径为,高的圆柱形水杯中,设筷子露在杯子外面的长度,则h的取值范围是( )
A. B. C. D.
8.如图,正方体盒子的棱长为4,中点为,一只蚂蚁从点沿正方体的表面爬到点,蚂蚁爬行的最短距离是( )
A.10 B. C. D.
9.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠BAC,ED⊥AB,则ED的长( )
A.3 B.4 C.5 D.6
10.如图所示,四边形中,,,,,且,则四边形的面积是( )
A. B. C. D.无法确定
二、填空题
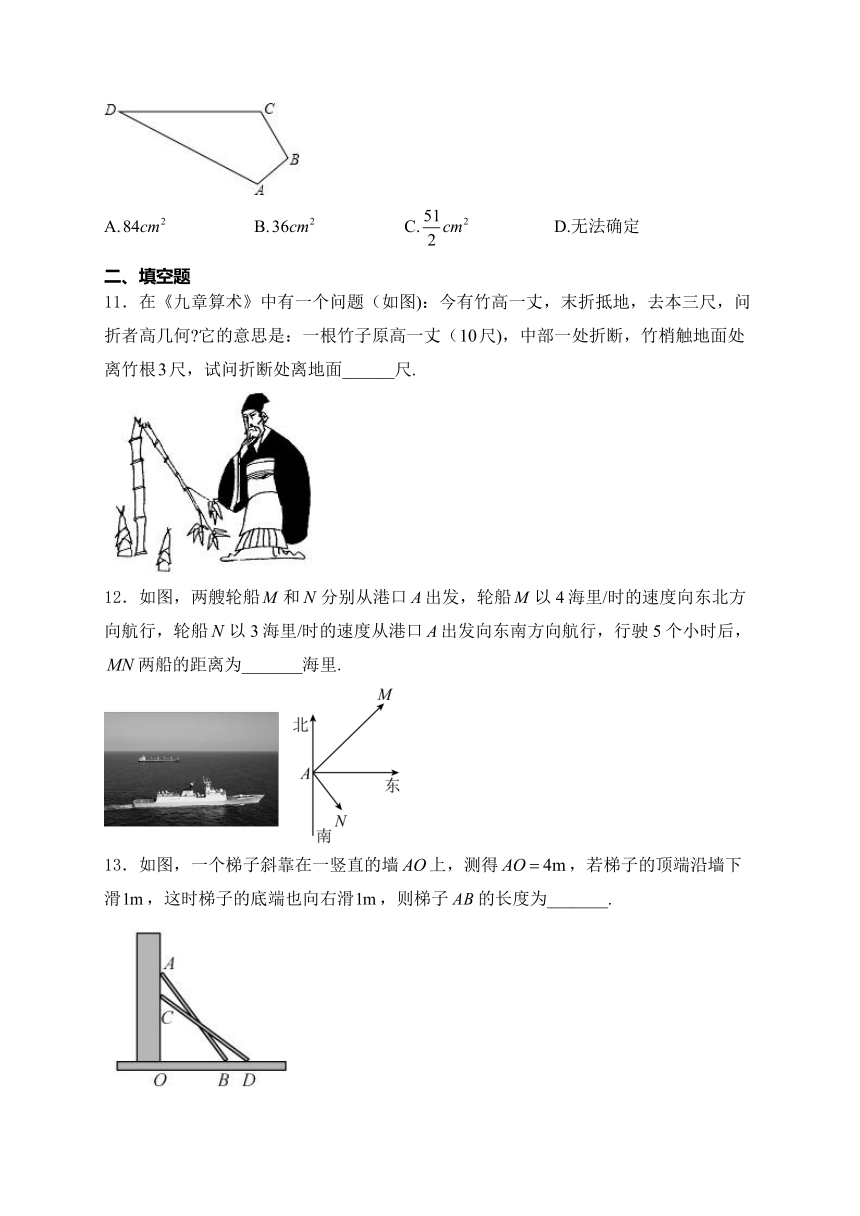
11.在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何 它的意思是:一根竹子原高一丈(尺),中部一处折断,竹梢触地面处离竹根尺,试问折断处离地面______尺.
12.如图,两艘轮船和分别从港口出发,轮船以4海里/时的速度向东北方向航行,轮船以3海里/时的速度从港口出发向东南方向航行,行驶5个小时后,两船的距离为_______海里.
13.如图,一个梯子斜靠在一竖直的墙上,测得,若梯子的顶端沿墙下滑,这时梯子的底端也向右滑,则梯子的长度为_______.
14.如图四边形中,,,,则四边形的面积是_____.
15.如图所示,已知中,,,,点P是边上的一个动点,点P从点B开始沿方向运动,且速度为每秒,设运动的时间为(),若是以为腰的等腰三角形,则运动时间_____.
三、解答题
16.在第十四届全国人大一次会议召开之际,某中学举行了庄严的升旗仪式.看着着冉升起的五星红旗(如图1),小乐想用刚学过的知识计算旗杆的高度.如图2,为旗杆上用来固定国旗的绳子,点距地面的高度.将绳子拉至的位置,测得点到的距离,到地面的垂直高度,求旗杆的高度.
17.如图,某工厂前面有一条笔直的公路,原来有两条路,可以从工厂到达公路,经测量,,,现需要修建一条路,使工厂到公路的路程最短.请你用尺规作图画出最短路径(不写画法,保留作图痕迹),并求出新建路的长.
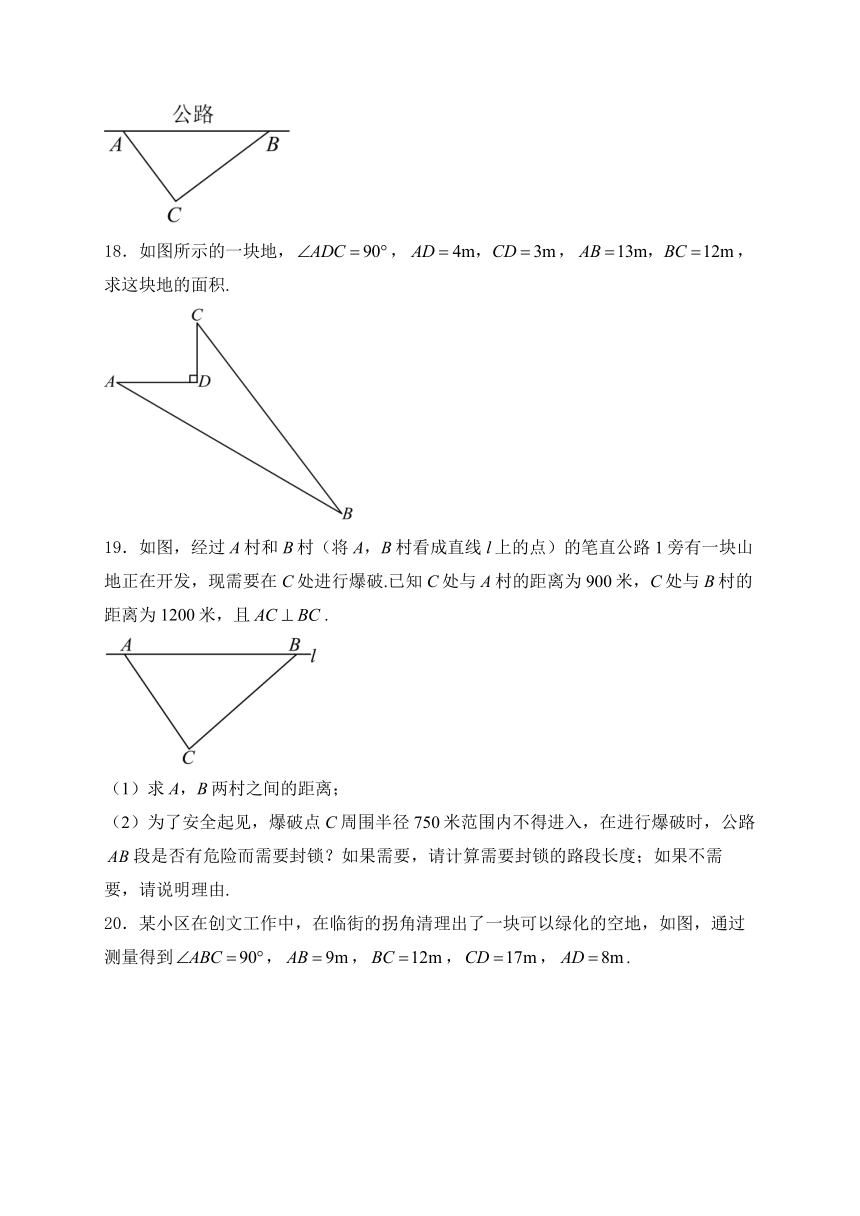
18.如图所示的一块地,,,,求这块地的面积.
19.如图,经过A村和B村(将A,B村看成直线l上的点)的笔直公路1旁有一块山地正在开发,现需要在C处进行爆破.已知C处与A村的距离为900米,C处与B村的距离为1200米,且.
(1)求A,B两村之间的距离;
(2)为了安全起见,爆破点C周围半径750米范围内不得进入,在进行爆破时,公路段是否有危险而需要封锁?如果需要,请计算需要封锁的路段长度;如果不需要,请说明理由.
20.某小区在创文工作中,在临街的拐角清理出了一块可以绿化的空地,如图,通过测量得到,,,,.
(1)求、两点之间的距离;
(2)若平均每平方米空地的绿化费用为150元,试计算绿化这片空地共需花费多少元?
参考答案
1.答案:D
解析:A、全等三角形的对应角相等的逆命题是对应角相等的三角形全等,不成立,不符合题意;
B、同位角互补,两直线平行的逆命题是两直线平行,同位角互补,不成立,不符合题意;
C、对顶角相等的逆命题是相等的角是对顶角,不成立,不符合题意;
D、若三角形的三边满足,则该三角形是直角三角形的逆命题是直角三角形的三边满足,成立,符合题意;
故选:D.
2.答案:D
解析:A.,故此选项不符合题意;
B.,故此选项不符合题意;
C.,故此选项不符合题意;
D.,故此选项符合题意;
故答案为:D.
3.答案:B
解析:∵,
∴,
∴,
∴,
∴,
∴是以为斜边的直角三角形;
故选B.
4.答案:A
解析:由勾股定理得:,
,
点A是以B为圆心,以为半径的圆与数轴的交点,且在左侧,
.
故选:A.
5.答案:B
解析:正方形的面积,
正方形的面积,
∵,
∴
故选:B
6.答案:D
解析:如图,,,,,
在中,
∵,
∴,
∴
∴,即小巷的宽度为2.7米.
故选:D.
7.答案:D
解析:如图,当筷子的底端在点时,筷子露在外面的长度最长,
∴,
当筷子的底端在点时,筷子露在杯子外面的长度最短,
在中,,,
∴,
此时,
所以取值范围是,
故选:D.
8.答案:B
解析:∵中点为,
∴,
当沿前面和上面爬行时,将正方体展开,连接,
,
在中,,
当沿前面和右面爬行时,将正方体展开,连接,
,
在中,,
,
故选:B.
9.答案:A
解析:∵在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴,
∵AE为△ABC的角平分线,∠ACB=90°,ED⊥AB,
∴DE=CE,
在Rt△ADE和Rt△ACE中,
∵AE=AE,DE=CE,
∴Rt△ADE≌Rt△ACE(HL),
∴AD=AC=6,∠ADE=90°
∴BD=10﹣6=4,
设DE=x,则CE=x,BE=8﹣x,
在Rt△BDE中,
,
即,
解得x=3,
所以ED的长是3,
故选:A.
10.答案:B
解析:连接,
,,,
,
,
,
,
,
,
即,
为直角三角形,
,
,
,
,
.
故选:B.
11.答案:4.55
解析:设折断处离地面尺,根据题意可得:
,
解得:,
答:折断处离地面4.55尺.
故答案为:4.55.
12.答案:25
解析:连接如图,
∵两船行驶的方向是东北方向和东南方向,
∴,
在中,(海里),(海里),
根据勾股定理得(海里).
故答案为:25.
13.答案:
解析:设,
由题意得:,,,
在中,根据勾股定理得:,
在中,根据勾股定理得:,
,
解得:,
,
即梯子的长为.
故答案为:.
14.答案:
解析:连接,
∵,
∴是等腰直角三角形,
在中,
∵,
∴,
∵,
∴,
∴是直角三角形,且,
∴四边形的面积
.
故答案为:.
15.答案:或或
解析:∵,,,
∴,
∴,
如图1,,
∴;
如图2,,
∴,
∴;
如图3,,
过点B作于D,则,
∵,
∴,
∴,
由勾股定理得:,
∴,
∴,
综上所述,t的值是或或.
故答案为:或或.
16.答案:
解析:∵,
∴,
∵,
∴,
设,则,,
由题意可得:,
在中,,
即,
解得:,即,
∴旗杆的高度为:.
17.答案:图见解析,
解析:过点作于点,则线段为新建公路.
,,
,,
,
是直角三角形.
,
,
新建路的长为.
18.答案:
解析:如图所示,连接,
∵,,
∴,
又∵,
∴,
∴是直角三角形,且,
∴.
19.答案:(1)1500米
(2)段公路需要封锁,需要封锁的路段长度为420米
解析:(1)在中,米,米,
(米).
答:A,B两村之间的距离为1500米;
(2)公路有危险而需要封锁.
理由如下:如图,过C作于D.以点C为圆心,750米为半径画弧,交于点E,F,连接,,
,
(米).
由于720米米,故有危险,
因此段公路需要封锁.
米,
(米),
故米,
则需要封锁的路段长度为420米.
20.答案:(1)
(2)17100元
解析:(1)∵,,,
∴;
(2)∵,,,
且,
∴,
∴,
∴,
,
∴,
∴(元),
答:绿化这片空地共需花费17100元.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列命题的逆命题成立的是( )
A.全等三角形的对应角相等
B.同位角互补,两直线平行
C.对顶角相等
D.若三角形三边满足,则该三角形是直角三角形
2.下列四组线段不能围成直角三角形的是( )
A.,, B.,,
C.,, D.,,
3.若的三边分别为,,,且满足,则是( )
A.以为斜边的直角三角形 B.以为斜边的直角三角形
C.以为斜边的直角三角形 D.不是直角三角形
4.如图所示,,,若数轴上点A所表示的数为a,则a的值为( )
A. B. C. D.
5.如图,在中,,若,则正方形和正方形的面积之和为( )
A. B. C. D.
6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙的距离为0.7米,顶端距离地面2.4米.若保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面1.5米,则小巷的宽度为( )
A.1.8米 B.2米 C.2.5米 D.2.7米
7.如图所示,将一根的筷子,置于底面直径为,高的圆柱形水杯中,设筷子露在杯子外面的长度,则h的取值范围是( )
A. B. C. D.
8.如图,正方体盒子的棱长为4,中点为,一只蚂蚁从点沿正方体的表面爬到点,蚂蚁爬行的最短距离是( )
A.10 B. C. D.
9.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠BAC,ED⊥AB,则ED的长( )
A.3 B.4 C.5 D.6
10.如图所示,四边形中,,,,,且,则四边形的面积是( )
A. B. C. D.无法确定
二、填空题
11.在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何 它的意思是:一根竹子原高一丈(尺),中部一处折断,竹梢触地面处离竹根尺,试问折断处离地面______尺.
12.如图,两艘轮船和分别从港口出发,轮船以4海里/时的速度向东北方向航行,轮船以3海里/时的速度从港口出发向东南方向航行,行驶5个小时后,两船的距离为_______海里.
13.如图,一个梯子斜靠在一竖直的墙上,测得,若梯子的顶端沿墙下滑,这时梯子的底端也向右滑,则梯子的长度为_______.
14.如图四边形中,,,,则四边形的面积是_____.
15.如图所示,已知中,,,,点P是边上的一个动点,点P从点B开始沿方向运动,且速度为每秒,设运动的时间为(),若是以为腰的等腰三角形,则运动时间_____.
三、解答题
16.在第十四届全国人大一次会议召开之际,某中学举行了庄严的升旗仪式.看着着冉升起的五星红旗(如图1),小乐想用刚学过的知识计算旗杆的高度.如图2,为旗杆上用来固定国旗的绳子,点距地面的高度.将绳子拉至的位置,测得点到的距离,到地面的垂直高度,求旗杆的高度.
17.如图,某工厂前面有一条笔直的公路,原来有两条路,可以从工厂到达公路,经测量,,,现需要修建一条路,使工厂到公路的路程最短.请你用尺规作图画出最短路径(不写画法,保留作图痕迹),并求出新建路的长.
18.如图所示的一块地,,,,求这块地的面积.
19.如图,经过A村和B村(将A,B村看成直线l上的点)的笔直公路1旁有一块山地正在开发,现需要在C处进行爆破.已知C处与A村的距离为900米,C处与B村的距离为1200米,且.
(1)求A,B两村之间的距离;
(2)为了安全起见,爆破点C周围半径750米范围内不得进入,在进行爆破时,公路段是否有危险而需要封锁?如果需要,请计算需要封锁的路段长度;如果不需要,请说明理由.
20.某小区在创文工作中,在临街的拐角清理出了一块可以绿化的空地,如图,通过测量得到,,,,.
(1)求、两点之间的距离;
(2)若平均每平方米空地的绿化费用为150元,试计算绿化这片空地共需花费多少元?
参考答案
1.答案:D
解析:A、全等三角形的对应角相等的逆命题是对应角相等的三角形全等,不成立,不符合题意;
B、同位角互补,两直线平行的逆命题是两直线平行,同位角互补,不成立,不符合题意;
C、对顶角相等的逆命题是相等的角是对顶角,不成立,不符合题意;
D、若三角形的三边满足,则该三角形是直角三角形的逆命题是直角三角形的三边满足,成立,符合题意;
故选:D.
2.答案:D
解析:A.,故此选项不符合题意;
B.,故此选项不符合题意;
C.,故此选项不符合题意;
D.,故此选项符合题意;
故答案为:D.
3.答案:B
解析:∵,
∴,
∴,
∴,
∴,
∴是以为斜边的直角三角形;
故选B.
4.答案:A
解析:由勾股定理得:,
,
点A是以B为圆心,以为半径的圆与数轴的交点,且在左侧,
.
故选:A.
5.答案:B
解析:正方形的面积,
正方形的面积,
∵,
∴
故选:B
6.答案:D
解析:如图,,,,,
在中,
∵,
∴,
∴
∴,即小巷的宽度为2.7米.
故选:D.
7.答案:D
解析:如图,当筷子的底端在点时,筷子露在外面的长度最长,
∴,
当筷子的底端在点时,筷子露在杯子外面的长度最短,
在中,,,
∴,
此时,
所以取值范围是,
故选:D.
8.答案:B
解析:∵中点为,
∴,
当沿前面和上面爬行时,将正方体展开,连接,
,
在中,,
当沿前面和右面爬行时,将正方体展开,连接,
,
在中,,
,
故选:B.
9.答案:A
解析:∵在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴,
∵AE为△ABC的角平分线,∠ACB=90°,ED⊥AB,
∴DE=CE,
在Rt△ADE和Rt△ACE中,
∵AE=AE,DE=CE,
∴Rt△ADE≌Rt△ACE(HL),
∴AD=AC=6,∠ADE=90°
∴BD=10﹣6=4,
设DE=x,则CE=x,BE=8﹣x,
在Rt△BDE中,
,
即,
解得x=3,
所以ED的长是3,
故选:A.
10.答案:B
解析:连接,
,,,
,
,
,
,
,
,
即,
为直角三角形,
,
,
,
,
.
故选:B.
11.答案:4.55
解析:设折断处离地面尺,根据题意可得:
,
解得:,
答:折断处离地面4.55尺.
故答案为:4.55.
12.答案:25
解析:连接如图,
∵两船行驶的方向是东北方向和东南方向,
∴,
在中,(海里),(海里),
根据勾股定理得(海里).
故答案为:25.
13.答案:
解析:设,
由题意得:,,,
在中,根据勾股定理得:,
在中,根据勾股定理得:,
,
解得:,
,
即梯子的长为.
故答案为:.
14.答案:
解析:连接,
∵,
∴是等腰直角三角形,
在中,
∵,
∴,
∵,
∴,
∴是直角三角形,且,
∴四边形的面积
.
故答案为:.
15.答案:或或
解析:∵,,,
∴,
∴,
如图1,,
∴;
如图2,,
∴,
∴;
如图3,,
过点B作于D,则,
∵,
∴,
∴,
由勾股定理得:,
∴,
∴,
综上所述,t的值是或或.
故答案为:或或.
16.答案:
解析:∵,
∴,
∵,
∴,
设,则,,
由题意可得:,
在中,,
即,
解得:,即,
∴旗杆的高度为:.
17.答案:图见解析,
解析:过点作于点,则线段为新建公路.
,,
,,
,
是直角三角形.
,
,
新建路的长为.
18.答案:
解析:如图所示,连接,
∵,,
∴,
又∵,
∴,
∴是直角三角形,且,
∴.
19.答案:(1)1500米
(2)段公路需要封锁,需要封锁的路段长度为420米
解析:(1)在中,米,米,
(米).
答:A,B两村之间的距离为1500米;
(2)公路有危险而需要封锁.
理由如下:如图,过C作于D.以点C为圆心,750米为半径画弧,交于点E,F,连接,,
,
(米).
由于720米米,故有危险,
因此段公路需要封锁.
米,
(米),
故米,
则需要封锁的路段长度为420米.
20.答案:(1)
(2)17100元
解析:(1)∵,,,
∴;
(2)∵,,,
且,
∴,
∴,
∴,
,
∴,
∴(元),
答:绿化这片空地共需花费17100元.
